Algorithmes de clustering - Clustering hiérarchique
Introduction au clustering hiérarchique
Le clustering hiérarchique est un autre algorithme d'apprentissage non supervisé utilisé pour regrouper les points de données non étiquetés ayant des caractéristiques similaires. Les algorithmes de clustering hiérarchique appartiennent aux deux catégories suivantes:
Agglomerative hierarchical algorithms- Dans les algorithmes hiérarchiques agglomératifs, chaque point de données est traité comme un seul cluster puis successivement fusionner ou agglomérer (approche ascendante) les paires de clusters. La hiérarchie des clusters est représentée sous la forme d'un dendrogramme ou d'une structure arborescente.
Divisive hierarchical algorithms - D'autre part, dans les algorithmes hiérarchiques de division, tous les points de données sont traités comme un grand cluster et le processus de clustering implique de diviser (approche descendante) le seul grand cluster en plusieurs petits clusters.
Étapes pour effectuer un clustering hiérarchique agglomératif
Nous allons expliquer le regroupement hiérarchique le plus utilisé et le plus important, c'est-à-dire agglomératif. Les étapes pour effectuer la même chose sont les suivantes -
Step 1- Traitez chaque point de données comme un seul cluster. Par conséquent, nous aurons, disons K clusters au début. Le nombre de points de données sera également K au début.
Step 2- Maintenant, dans cette étape, nous devons former un grand cluster en joignant deux points de données de placard. Cela se traduira par un total de clusters K-1.
Step 3- Maintenant, pour former plus de clusters, nous devons rejoindre deux clusters de placards. Cela se traduira par un total de clusters K-2.
Step 4 - Maintenant, pour former un gros cluster, répétez les trois étapes ci-dessus jusqu'à ce que K devienne 0, c'est-à-dire qu'il ne reste plus de points de données à rejoindre.
Step 5 - Enfin, après avoir fait un seul gros cluster, les dendrogrammes seront utilisés pour se diviser en plusieurs clusters en fonction du problème.
Rôle des dendrogrammes dans le clustering hiérarchique agglomératif
Comme nous l'avons discuté dans la dernière étape, le rôle du dendrogramme commence une fois que le grand cluster est formé. Le dendrogramme sera utilisé pour diviser les clusters en plusieurs clusters de points de données liés en fonction de notre problème. Il peut être compris à l'aide de l'exemple suivant -
Exemple 1
Pour comprendre, commençons par importer les bibliothèques requises comme suit -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as npEnsuite, nous allons tracer les points de données que nous avons pris pour cet exemple -
X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],])
labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True Position')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom')
plt.show()
À partir du diagramme ci-dessus, il est très facile de voir que nous avons deux clusters dans les points de données, mais dans les données du monde réel, il peut y avoir des milliers de clusters. Ensuite, nous allons tracer les dendrogrammes de nos points de données en utilisant la bibliothèque Scipy -
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
linked = linkage(X, 'single')
labelList = range(1, 11)
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True)
plt.show()
Désormais, une fois le grand cluster formé, la plus longue distance verticale est sélectionnée. Une ligne verticale est ensuite dessinée à travers elle comme indiqué dans le diagramme suivant. Lorsque la ligne horizontale traverse la ligne bleue en deux points, le nombre de groupes serait de deux.

Ensuite, nous devons importer la classe pour le clustering et appeler sa méthode fit_predict pour prédire le cluster. Nous importons la classe AgglomerativeClustering de la bibliothèque sklearn.cluster -
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)Ensuite, tracez le cluster à l'aide du code suivant -
plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')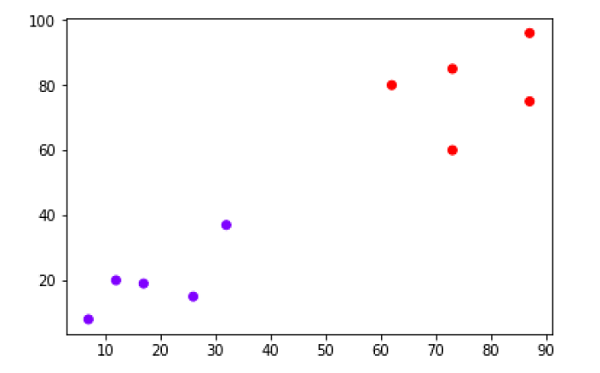
Le diagramme ci-dessus montre les deux clusters de nos points de données.
Exemple2
Comme nous avons compris le concept de dendrogrammes à partir de l'exemple simple discuté ci-dessus, passons à un autre exemple dans lequel nous créons des grappes du point de données dans Pima Indian Diabetes Dataset en utilisant le clustering hiérarchique -
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
import numpy as np
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
data.shape
(768, 9)
data.head()| slno. | preg | Plas | Prés | peau | tester | Masse | pédi | âge | classe |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33,6 | 0,627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26,6 | 0,351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23,3 | 0,672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28,1 | 0,167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43,1 | 2,288 | 33 | 1 |
patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
cluster.fit_predict(patient_data)
plt.figure(figsize=(10, 7))
plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')