Machine Learning avec Python - Guide rapide
Nous vivons à l'ère des données enrichies d'une meilleure puissance de calcul et de plus de ressources de stockage. Ces données ou informations augmentent de jour en jour, mais le vrai défi est de donner un sens à toutes les données. Les entreprises et les organisations tentent d'y faire face en construisant des systèmes intelligents utilisant les concepts et les méthodologies de la science des données, de l'exploration de données et de l'apprentissage automatique. Parmi eux, l'apprentissage automatique est le domaine le plus passionnant de l'informatique. Ce ne serait pas faux si nous appelons l'apprentissage automatique l'application et la science des algorithmes qui donnent du sens aux données.
Qu'est-ce que l'apprentissage automatique?
L'apprentissage automatique (ML) est ce domaine de l'informatique à l'aide duquel les systèmes informatiques peuvent donner du sens aux données de la même manière que les êtres humains.
En termes simples, ML est un type d'intelligence artificielle qui extrait des modèles à partir de données brutes à l'aide d'un algorithme ou d'une méthode. L'objectif principal du ML est de permettre aux systèmes informatiques d'apprendre de l'expérience sans être explicitement programmés ou d'intervention humaine.
Besoin d'apprentissage automatique
Les êtres humains, en ce moment, sont les espèces les plus intelligentes et les plus avancées sur terre car ils peuvent penser, évaluer et résoudre des problèmes complexes. De l'autre côté, l'IA en est encore à son stade initial et n'a pas dépassé l'intelligence humaine à bien des égards. Ensuite, la question est de savoir quel est le besoin de faire apprendre la machine? La raison la plus appropriée pour ce faire est «de prendre des décisions, basées sur des données, avec efficacité et échelle».
Dernièrement, les organisations investissent massivement dans les nouvelles technologies telles que l'intelligence artificielle, l'apprentissage automatique et l'apprentissage profond pour obtenir les informations clés des données pour effectuer plusieurs tâches du monde réel et résoudre des problèmes. On peut appeler cela des décisions basées sur les données prises par des machines, notamment pour automatiser le processus. Ces décisions basées sur les données peuvent être utilisées, au lieu d'utiliser la logique de programmation, dans les problèmes qui ne peuvent pas être programmés de manière intrinsèque. Le fait est que nous ne pouvons pas nous passer de l'intelligence humaine, mais un autre aspect est que nous devons tous résoudre les problèmes du monde réel avec efficacité à grande échelle. C'est pourquoi le besoin d'apprentissage automatique se fait sentir.
Pourquoi et quand faire apprendre les machines?
Nous avons déjà discuté de la nécessité de l'apprentissage automatique, mais une autre question se pose: dans quels scénarios devons-nous faire apprendre la machine? Il peut y avoir plusieurs circonstances où nous avons besoin de machines pour prendre des décisions basées sur les données avec efficacité et à grande échelle. Voici quelques-unes de ces circonstances où faire apprendre des machines serait plus efficace -
Manque d'expertise humaine
Le tout premier scénario dans lequel nous voulons qu'une machine apprenne et prenne des décisions basées sur les données peut être le domaine où il y a un manque d'expertise humaine. Les exemples peuvent être des navigations dans des territoires inconnus ou des planètes spatiales.
Scénarios dynamiques
Certains scénarios sont de nature dynamique, c'est-à-dire qu'ils changent avec le temps. Dans le cas de ces scénarios et comportements, nous voulons qu'une machine apprenne et prenne des décisions basées sur les données. Certains des exemples peuvent être la connectivité réseau et la disponibilité de l'infrastructure dans une organisation.
Difficulté à traduire l'expertise en tâches de calcul
Les humains peuvent avoir leur expertise dans divers domaines; cependant, ils sont incapables de traduire cette expertise en tâches de calcul. Dans de telles circonstances, nous voulons l'apprentissage automatique. Les exemples peuvent être les domaines de la reconnaissance vocale, des tâches cognitives, etc.
Modèle d'apprentissage automatique
Avant de discuter du modèle d'apprentissage automatique, nous devons comprendre la définition formelle suivante du ML donnée par le professeur Mitchell -
«On dit qu'un programme informatique apprend de l'expérience E en ce qui concerne une certaine classe de tâches T et une mesure de performance P, si ses performances aux tâches de T, telles que mesurées par P, s'améliorent avec l'expérience E.»
La définition ci-dessus se concentre essentiellement sur trois paramètres, également les principaux composants de tout algorithme d'apprentissage, à savoir la tâche (T), la performance (P) et l'expérience (E). Dans ce contexte, nous pouvons simplifier cette définition comme -
Le ML est un domaine de l'IA constitué d'algorithmes d'apprentissage qui -
Améliorer leurs performances (P)
Lors de l'exécution d'une tâche (T)
Au fil du temps avec l'expérience (E)
Sur la base de ce qui précède, le diagramme suivant représente un modèle d'apprentissage automatique -

Parlons-en plus en détail maintenant -
Tâche (T)
Du point de vue du problème, nous pouvons définir la tâche T comme le problème du monde réel à résoudre. Le problème peut être quelque chose comme trouver le meilleur prix de l'immobilier dans un endroit spécifique ou trouver la meilleure stratégie marketing, etc. D'un autre côté, si nous parlons d'apprentissage automatique, la définition de la tâche est différente car il est difficile de résoudre les tâches basées sur le ML en approche de programmation conventionnelle.
Une tâche T est dite être une tâche basée sur le ML lorsqu'elle est basée sur le processus et que le système doit suivre pour fonctionner sur des points de données. Les exemples de tâches basées sur le ML sont la classification, la régression, l'annotation structurée, le clustering, la transcription, etc.
Expérience (E)
Comme son nom l'indique, ce sont les connaissances acquises à partir des points de données fournis à l'algorithme ou au modèle. Une fois fourni avec le jeu de données, le modèle s'exécutera de manière itérative et apprendra un modèle inhérent. L'apprentissage ainsi acquis est appelé expérience (E). En faisant une analogie avec l'apprentissage humain, nous pouvons penser à cette situation comme dans laquelle un être humain apprend ou acquiert de l'expérience à partir de divers attributs tels que la situation, les relations, etc. L'apprentissage supervisé, non supervisé et par renforcement sont des moyens d'apprendre ou d'acquérir de l'expérience. L'expérience acquise par notre modèle ou algorithme ML sera utilisée pour résoudre la tâche T.
Performance (P)
Un algorithme ML est censé effectuer une tâche et acquérir de l'expérience avec le passage du temps. La mesure qui indique si l'algorithme ML fonctionne comme prévu ou non est sa performance (P). P est essentiellement une métrique quantitative qui indique comment un modèle exécute la tâche, T, en utilisant son expérience, E. Il existe de nombreuses métriques qui aident à comprendre les performances de ML, telles que le score de précision, le score F1, la matrice de confusion, la précision, le rappel , sensibilité etc.
Défis de l'apprentissage automatique
Alors que l'apprentissage automatique évolue rapidement, faisant des progrès significatifs en matière de cybersécurité et de voitures autonomes, ce segment de l'IA dans son ensemble a encore un long chemin à parcourir. La raison en est que le ML n'a pas été en mesure de surmonter un certain nombre de défis. Les défis auxquels le ML est actuellement confronté sont:
Quality of data- Avoir des données de bonne qualité pour les algorithmes ML est l'un des plus grands défis. L'utilisation de données de mauvaise qualité entraîne des problèmes liés au prétraitement des données et à l'extraction des caractéristiques.
Time-Consuming task - Un autre défi auquel sont confrontés les modèles ML est la consommation de temps, en particulier pour l'acquisition de données, l'extraction de caractéristiques et la récupération.
Lack of specialist persons - La technologie ML étant encore à ses balbutiements, la disponibilité de ressources d'experts est un travail difficile.
No clear objective for formulating business problems - Ne pas avoir d'objectif clair et d'objectif bien défini pour les problèmes commerciaux est un autre défi majeur pour le ML, car cette technologie n'est pas encore aussi mature.
Issue of overfitting & underfitting - Si le modèle est sur-ajusté ou sous-ajusté, il ne peut pas être bien représenté pour le problème.
Curse of dimensionality- Un autre défi auquel le modèle ML est confronté est le trop grand nombre de fonctionnalités des points de données. Cela peut être un réel obstacle.
Difficulty in deployment - La complexité du modèle ML rend son déploiement dans la vraie vie assez difficile.
Applications de l'apprentissage automatique
L'apprentissage automatique est la technologie à la croissance la plus rapide et, selon les chercheurs, nous sommes dans l'année d'or de l'IA et du ML. Il est utilisé pour résoudre de nombreux problèmes complexes du monde réel qui ne peuvent pas être résolus avec une approche traditionnelle. Voici quelques applications concrètes du ML -
Analyse des émotions
Analyse des sentiments
Détection et prévention des erreurs
Prévisions et prévisions météorologiques
Analyse et prévisions boursières
Synthèse de discours
Reconnaissance de la parole
Segmentation de la clientèle
Reconnaissance d'objets
Détection de fraude
Prévention de la fraude
Recommandation de produits au client dans les achats en ligne.
Une introduction à Python
Python est un langage de programmation orienté objet populaire ayant les capacités d'un langage de programmation de haut niveau. Sa syntaxe facile à apprendre et sa capacité de portabilité le rendent populaire de nos jours. Les faits suivants nous donnent une introduction à Python -
Python a été développé par Guido van Rossum au Stichting Mathematisch Centrum aux Pays-Bas.
Il a été écrit comme le successeur du langage de programmation nommé «ABC».
Sa première version est sortie en 1991.
Le nom Python a été choisi par Guido van Rossum dans une émission de télévision intitulée Monty Python's Flying Circus.
C'est un langage de programmation open source, ce qui signifie que nous pouvons le télécharger gratuitement et l'utiliser pour développer des programmes. Il peut être téléchargé sur www.python.org .
Le langage de programmation Python possède les fonctionnalités de Java et C à la fois. Il a le code élégant «C» et d'autre part, il a des classes et des objets comme Java pour la programmation orientée objet.
C'est un langage interprété, ce qui signifie que le code source du programme Python serait d'abord converti en bytecode puis exécuté par la machine virtuelle Python.
Forces et faiblesses de Python
Chaque langage de programmation a des forces et des faiblesses, tout comme Python.
Forces
Selon des études et des sondages, Python est le cinquième langage le plus important ainsi que le langage le plus populaire pour l'apprentissage automatique et la science des données. C'est à cause des atouts suivants que Python a -
Easy to learn and understand- La syntaxe de Python est plus simple; il est donc relativement facile, même pour les débutants aussi, d'apprendre et de comprendre la langue.
Multi-purpose language - Python est un langage de programmation polyvalent car il prend en charge la programmation structurée, la programmation orientée objet ainsi que la programmation fonctionnelle.
Huge number of modules- Python a un grand nombre de modules pour couvrir tous les aspects de la programmation. Ces modules sont facilement disponibles pour une utilisation faisant de Python un langage extensible.
Support of open source community- En tant que langage de programmation open source, Python est pris en charge par une très large communauté de développeurs. Pour cette raison, les bogues sont facilement corrigés par la communauté Python. Cette caractéristique rend Python très robuste et adaptatif.
Scalability - Python est un langage de programmation évolutif car il fournit une structure améliorée pour la prise en charge de grands programmes par rapport aux scripts shell.
La faiblesse
Bien que Python soit un langage de programmation populaire et puissant, il a sa propre faiblesse de vitesse d'exécution lente.
La vitesse d'exécution de Python est lente par rapport aux langages compilés car Python est un langage interprété. Cela peut être le principal domaine d'amélioration pour la communauté Python.
Installer Python
Pour travailler en Python, il faut d'abord l'installer. Vous pouvez effectuer l'installation de Python de l'une des deux manières suivantes -
Installer Python individuellement
Utilisation de la distribution Python pré-packagée - Anaconda
Discutons-en chacun en détail.
Installer Python individuellement
Si vous souhaitez installer Python sur votre ordinateur, vous devez télécharger uniquement le code binaire applicable à votre plate-forme. La distribution Python est disponible pour les plates-formes Windows, Linux et Mac.
Ce qui suit est un bref aperçu de l'installation de Python sur les plates-formes mentionnées ci-dessus -
On Unix and Linux platform
À l'aide des étapes suivantes, nous pouvons installer Python sur les plates-formes Unix et Linux -
Tout d'abord, allez à https://www.python.org/downloads/.
Ensuite, cliquez sur le lien pour télécharger le code source compressé disponible pour Unix / Linux.
Maintenant, téléchargez et extrayez des fichiers.
Ensuite, nous pouvons éditer le fichier Modules / Setup si nous voulons personnaliser certaines options.
Ensuite, écrivez la commande run ./configure script
make
faire installer
On Windows platform
À l'aide des étapes suivantes, nous pouvons installer Python sur la plate-forme Windows -
Tout d'abord, allez à https://www.python.org/downloads/.
Ensuite, cliquez sur le lien pour le fichier python-XYZ.msi du programme d'installation de Windows. Ici XYZ est la version que nous souhaitons installer.
Maintenant, nous devons exécuter le fichier qui est téléchargé. Cela nous mènera à l'assistant d'installation de Python, qui est facile à utiliser. Maintenant, acceptez les paramètres par défaut et attendez que l'installation soit terminée.
On Macintosh platform
Pour Mac OS X, Homebrew, un programme d'installation de package génial et facile à utiliser est recommandé pour installer Python 3. Si vous n'avez pas Homebrew, vous pouvez l'installer à l'aide de la commande suivante -
$ ruby -e "$(curl -fsSL
https://raw.githubusercontent.com/Homebrew/install/master/install)"Il peut être mis à jour avec la commande ci-dessous -
$ brew updateMaintenant, pour installer Python3 sur votre système, nous devons exécuter la commande suivante -
$ brew install python3Utilisation de la distribution Python pré-packagée: Anaconda
Anaconda est une compilation packagée de Python qui contient toutes les bibliothèques largement utilisées en science des données. Nous pouvons suivre les étapes suivantes pour configurer l'environnement Python à l'aide d'Anaconda -
Step1- Tout d'abord, nous devons télécharger le package d'installation requis à partir de la distribution Anaconda. Le lien pour le même esthttps://www.anaconda.com/distribution/. Vous pouvez choisir entre Windows, Mac et Linux OS selon vos besoins.
Step2- Ensuite, sélectionnez la version Python que vous souhaitez installer sur votre machine. La dernière version de Python est la 3.7. Là, vous obtiendrez les options pour l'installateur graphique 64 bits et 32 bits.
Step3- Après avoir sélectionné la version du système d'exploitation et de Python, il téléchargera le programme d'installation d'Anaconda sur votre ordinateur. Maintenant, double-cliquez sur le fichier et le programme d'installation installera le package Anaconda.
Step4 - Pour vérifier s'il est installé ou non, ouvrez une invite de commande et tapez Python comme suit -

Vous pouvez également vérifier cela dans une conférence vidéo détaillée à l'adressehttps://www.tutorialspoint.com/python_essentials_online_training/getting_started_with_anaconda.asp.
Pourquoi Python pour la science des données?
Python est le cinquième langage le plus important ainsi que le langage le plus populaire pour l'apprentissage automatique et la science des données. Voici les caractéristiques de Python qui en font le choix de langage préféré pour la science des données -
Ensemble complet de packages
Python dispose d'un ensemble complet et puissant de packages prêts à être utilisés dans divers domaines. Il contient également des packages tels que numpy, scipy, pandas, scikit-learn, etc., nécessaires à l'apprentissage automatique et à la science des données.
Prototypage facile
Une autre caractéristique importante de Python qui en fait le choix du langage pour la science des données est le prototypage facile et rapide. Cette fonctionnalité est utile pour développer un nouvel algorithme.
Fonction de collaboration
Le domaine de la science des données a fondamentalement besoin d'une bonne collaboration et Python fournit de nombreux outils utiles qui rendent cela extrêmement.
Une langue pour de nombreux domaines
Un projet de science des données typique comprend divers domaines tels que l'extraction de données, la manipulation de données, l'analyse de données, l'extraction de fonctionnalités, la modélisation, l'évaluation, le déploiement et la mise à jour de la solution. Comme Python est un langage polyvalent, il permet au data scientist d'adresser tous ces domaines à partir d'une plateforme commune.
Composants de l'écosystème Python ML
Dans cette section, laissez-nous discuter de certaines bibliothèques de base de Data Science qui forment les composants de l'écosystème Python Machine Learning. Ces composants utiles font de Python un langage important pour la science des données. Bien qu'il existe de nombreux composants de ce type, discutons ici de certains des composants importants de l'écosystème Python -
Cahier Jupyter
Les notebooks Jupyter fournissent essentiellement un environnement de calcul interactif pour le développement d'applications de science des données basées sur Python. Ils sont anciennement connus sous le nom de notebooks ipython. Voici quelques-unes des fonctionnalités des notebooks Jupyter qui en font l'un des meilleurs composants de l'écosystème Python ML -
Les blocs-notes Jupyter peuvent illustrer le processus d'analyse étape par étape en organisant les éléments tels que le code, les images, le texte, la sortie, etc., étape par étape.
Il aide un data scientist à documenter le processus de réflexion tout en développant le processus d'analyse.
On peut également capturer le résultat comme partie du cahier.
Avec l'aide des cahiers Jupyter, nous pouvons également partager notre travail avec un pair.
Installation et exécution
Si vous utilisez la distribution Anaconda, vous n'avez pas besoin d'installer jupyter notebook séparément car il est déjà installé avec lui. Il vous suffit d'aller à l'invite Anaconda et de taper la commande suivante -
C:\>jupyter notebookAprès avoir appuyé sur Entrée, il démarrera un serveur notebook sur localhost: 8888 de votre ordinateur. Il est montré dans la capture d'écran suivante -

Maintenant, après avoir cliqué sur l'onglet Nouveau, vous obtiendrez une liste d'options. Sélectionnez Python 3 et il vous mènera au nouveau bloc-notes pour commencer à y travailler. Vous en aurez un aperçu dans les captures d'écran suivantes -


D'autre part, si vous utilisez une distribution Python standard, jupyter notebook peut être installé à l'aide du programme d'installation de packages python populaire, pip.
pip install jupyterTypes de cellules dans Jupyter Notebook
Voici les trois types de cellules dans un notebook Jupyter -
Code cells- Comme son nom l'indique, nous pouvons utiliser ces cellules pour écrire du code. Après avoir écrit le code / contenu, il l'enverra au noyau associé au notebook.
Markdown cells- Nous pouvons utiliser ces cellules pour noter le processus de calcul. Ils peuvent contenir des éléments tels que du texte, des images, des équations Latex, des balises HTML, etc.
Raw cells- Le texte qui y est écrit est affiché tel quel. Ces cellules sont essentiellement utilisées pour ajouter le texte que nous ne souhaitons pas convertir par le mécanisme de conversion automatique de jupyter notebook.
Pour une étude plus détaillée du notebook jupyter, vous pouvez aller sur le lienhttps://www.tutorialspoint.com/jupyter/index.htm.
NumPy
C'est un autre composant utile qui fait de Python l'un des langages préférés de la science des données. Il signifie essentiellement Python numérique et se compose d'objets de tableau multidimensionnel. En utilisant NumPy, nous pouvons effectuer les opérations importantes suivantes -
Opérations mathématiques et logiques sur les tableaux.
Transformation de Fourier
Opérations associées à l'algèbre linéaire.
Nous pouvons également voir NumPy comme le remplacement de MatLab car NumPy est principalement utilisé avec Scipy (Scientific Python) et Mat-plotlib (bibliothèque de traçage).
Installation and Execution
Si vous utilisez la distribution Anaconda, vous n'avez pas besoin d'installer NumPy séparément car il est déjà installé avec. Il vous suffit d'importer le package dans votre script Python à l'aide de:
import numpy as npD'un autre côté, si vous utilisez une distribution Python standard, NumPy peut être installé à l'aide du programme d'installation de package python populaire, pip.
pip install NumPyPour une étude plus détaillée de NumPy, vous pouvez aller sur le lienhttps://www.tutorialspoint.com/numpy/index.htm.
Pandas
C'est une autre bibliothèque Python utile qui fait de Python l'un des langages préférés de la science des données. Pandas est essentiellement utilisé pour la manipulation, la lutte et l'analyse des données. Il a été développé par Wes McKinney en 2008. Avec l'aide de Pandas, dans le traitement des données, nous pouvons accomplir les cinq étapes suivantes -
Load
Prepare
Manipulate
Model
Analyze
Représentation des données dans les pandas
La représentation complète des données dans Pandas se fait à l'aide des trois structures de données suivantes -
Series- Il s'agit essentiellement d'un ndarray unidimensionnel avec une étiquette d'axe, ce qui signifie que c'est comme un simple tableau avec des données homogènes. Par exemple, la série suivante est une collection d'entiers 1,5,10,15,24,25…
| 1 | 5 | dix | 15 | 24 | 25 | 28 | 36 | 40 | 89 |
Data frame- C'est la structure de données la plus utile et utilisée pour presque tous les types de représentation et de manipulation de données dans les pandas. Il s'agit essentiellement d'une structure de données bidimensionnelle qui peut contenir des données hétérogènes. En règle générale, les données tabulaires sont représentées à l'aide de blocs de données. Par exemple, le tableau suivant montre les données des élèves ayant leurs noms et numéros de rôle, âge et sexe -
Nom |
Numéro de rôle |
Âge |
Le sexe |
|---|---|---|---|
Aarav |
1 |
15 |
Masculin |
Harshit |
2 |
14 |
Masculin |
Kanika |
3 |
16 |
Femme |
Mayank |
4 |
15 |
Masculin |
Panel- Il s'agit d'une structure de données tridimensionnelle contenant des données hétérogènes. Il est très difficile de représenter le panneau sous forme de représentation graphique, mais il peut être illustré comme un conteneur de DataFrame.
Le tableau suivant nous donne la dimension et la description des structures de données mentionnées ci-dessus utilisées dans Pandas -
Structure de données |
Dimension |
La description |
|---|---|---|
Séries |
1-D |
Taille immuable, données homogènes 1-D |
DataFrames |
2-D |
Taille Mutable, Données hétérogènes sous forme de tableau |
Panneau |
3-D |
Tableau de taille modifiable, conteneur de DataFrame. |
Nous pouvons comprendre ces structures de données car la structure de données de dimension supérieure est le conteneur de la structure de données de dimension inférieure.
Installation et exécution
Si vous utilisez la distribution Anaconda, il n'est pas nécessaire d'installer Pandas séparément car il est déjà installé avec. Il vous suffit d'importer le package dans votre script Python à l'aide de:
import pandas as pdD'autre part, si vous utilisez une distribution Python standard, Pandas peut être installé à l'aide du programme d'installation de packages python populaire, pip.
pip install PandasAprès avoir installé Pandas, vous pouvez l'importer dans votre script Python comme indiqué ci-dessus.
Exemple
Voici un exemple de création d'une série à partir de ndarray à l'aide de Pandas -
In [1]: import pandas as pd
In [2]: import numpy as np
In [3]: data = np.array(['g','a','u','r','a','v'])
In [4]: s = pd.Series(data)
In [5]: print (s)
0 g
1 a
2 u
3 r
4 a
5 v
dtype: objectPour une étude plus détaillée des Pandas, vous pouvez aller sur le lien https://www.tutorialspoint.com/python_pandas/index.htm.
Scikit-learn
Une autre bibliothèque python utile et la plus importante pour la science des données et l'apprentissage automatique en Python est Scikit-learn. Voici quelques fonctionnalités de Scikit-learn qui le rendent si utile -
Il est construit sur NumPy, SciPy et Matplotlib.
C'est un open source et peut être réutilisé sous licence BSD.
Il est accessible à tous et peut être réutilisé dans différents contextes.
Une large gamme d'algorithmes d'apprentissage automatique couvrant les principaux domaines de l'apprentissage automatique tels que la classification, le clustering, la régression, la réduction de la dimensionnalité, la sélection de modèles, etc.
Installation et exécution
Si vous utilisez la distribution Anaconda, alors pas besoin d'installer Scikit-learn séparément car il est déjà installé avec lui. Il vous suffit d'utiliser le package dans votre script Python. Par exemple, avec la ligne de script suivante, nous importons un ensemble de données de patientes atteintes d'un cancer du sein à partir deScikit-learn -
from sklearn.datasets import load_breast_cancerD'un autre côté, si vous utilisez une distribution Python standard et que vous avez NumPy et SciPy, Scikit-learn peut être installé à l'aide du programme d'installation de packages python populaire, pip.
pip install -U scikit-learnAprès avoir installé Scikit-learn, vous pouvez l'utiliser dans votre script Python comme vous l'avez fait ci-dessus.
Il existe divers algorithmes, techniques et méthodes de ML qui peuvent être utilisés pour créer des modèles permettant de résoudre des problèmes réels à l'aide de données. Dans ce chapitre, nous allons discuter de ces différents types de méthodes.
Différents types de méthodes
Voici différentes méthodes de ML basées sur certaines grandes catégories -
Basé sur une supervision humaine
Dans le processus d'apprentissage, certaines des méthodes basées sur la supervision humaine sont les suivantes:
Supervised Learning
Les algorithmes ou méthodes d'apprentissage supervisé sont les algorithmes de ML les plus couramment utilisés. Cette méthode ou cet algorithme d'apprentissage prend l'échantillon de données, c'est-à-dire les données d'apprentissage et leur sortie associée, c'est-à-dire les étiquettes ou les réponses avec chaque échantillon de données pendant le processus d'apprentissage.
L'objectif principal des algorithmes d'apprentissage supervisé est d'apprendre une association entre les échantillons de données d'entrée et les sorties correspondantes après avoir exécuté plusieurs instances de données d'apprentissage.
Par exemple, nous avons
x: variables d'entrée et
Y: variable de sortie
Maintenant, appliquez un algorithme pour apprendre la fonction de mappage de l'entrée à la sortie comme suit -
Y = f (x)
Maintenant, l'objectif principal serait d'approximer la fonction de mappage si bien que même lorsque nous avons de nouvelles données d'entrée (x), nous pouvons facilement prédire la variable de sortie (Y) pour ces nouvelles données d'entrée.
On l'appelle supervisé parce que tout le processus d'apprentissage peut être pensé tel qu'il est supervisé par un enseignant ou un superviseur. Des exemples d'algorithmes d'apprentissage automatique supervisé comprennentDecision tree, Random Forest, KNN, Logistic Regression etc.
Sur la base des tâches ML, les algorithmes d'apprentissage supervisé peuvent être divisés en deux grandes classes:
Classification
Regression
Classification
L'objectif principal des tâches basées sur la classification est de prédire les étiquettes de sortie catégorielles ou les réponses pour les données d'entrée données. Le résultat sera basé sur ce que le modèle a appris lors de la phase de formation. Comme nous savons que les réponses de sortie catégorielles signifient des valeurs non ordonnées et discrètes, chaque réponse de sortie appartiendra à une classe ou à une catégorie spécifique. Nous discuterons également en détail de la classification et des algorithmes associés dans les prochains chapitres.
Regression
L'objectif principal des tâches basées sur la régression est de prédire les étiquettes de sortie ou les réponses qui sont des valeurs numériques continues, pour les données d'entrée données. Le résultat sera basé sur ce que le modèle a appris dans sa phase de formation. Fondamentalement, les modèles de régression utilisent les caractéristiques des données d'entrée (variables indépendantes) et leurs valeurs de sortie numériques continues correspondantes (variables dépendantes ou de résultat) pour apprendre une association spécifique entre les entrées et les sorties correspondantes. Nous discuterons également en détail de la régression et des algorithmes associés dans d'autres chapitres.
Apprentissage non supervisé
Comme son nom l'indique, il est opposé aux méthodes ou algorithmes de ML supervisés, ce qui signifie que dans les algorithmes d'apprentissage automatique non supervisés, nous n'avons aucun superviseur pour fournir des conseils. Les algorithmes d'apprentissage non supervisé sont pratiques dans le scénario dans lequel nous n'avons pas la liberté, comme dans les algorithmes d'apprentissage supervisé, d'avoir des données d'apprentissage pré-étiquetées et nous voulons extraire un modèle utile des données d'entrée.
Par exemple, il peut être compris comme suit -
Supposons que nous ayons -
x: Input variables, alors il n'y aurait pas de variable de sortie correspondante et les algorithmes doivent découvrir le modèle intéressant dans les données pour l'apprentissage.
Des exemples d'algorithmes d'apprentissage automatique non supervisés incluent le clustering K-means, K-nearest neighbors etc.
Sur la base des tâches ML, les algorithmes d'apprentissage non supervisé peuvent être divisés en grandes classes suivantes:
Clustering
Association
Réduction de dimensionnalité
Clustering
Les méthodes de clustering sont l'une des méthodes de ML non supervisées les plus utiles. Ces algorithmes étaient utilisés pour trouver des similitudes ainsi que des modèles de relations entre des échantillons de données, puis regrouper ces échantillons en groupes ayant une similitude basée sur des caractéristiques. L'exemple réel du clustering est de regrouper les clients en fonction de leur comportement d'achat.
Association
Une autre méthode de ML non supervisée utile est Associationqui est utilisé pour analyser un grand ensemble de données pour trouver des modèles qui représentent en outre les relations intéressantes entre divers éléments. Il est également appeléAssociation Rule Mining ou Market basket analysis qui est principalement utilisé pour analyser les habitudes d'achat des clients.
Dimensionality Reduction
Cette méthode ML non supervisée est utilisée pour réduire le nombre de variables de fonctionnalité pour chaque échantillon de données en sélectionnant un ensemble de fonctionnalités principales ou représentatives. Une question se pose ici est la suivante: pourquoi devons-nous réduire la dimensionnalité? La raison en est le problème de la complexité de l'espace des fonctionnalités qui se pose lorsque nous commençons à analyser et à extraire des millions d'entités à partir d'échantillons de données. Ce problème se réfère généralement à la «malédiction de la dimensionnalité». L'ACP (analyse en composantes principales), les K-plus proches voisins et l'analyse discriminante sont quelques-uns des algorithmes populaires à cet effet.
Anomaly Detection
Cette méthode ML non supervisée est utilisée pour découvrir les occurrences d'événements rares ou d'observations qui ne se produisent généralement pas. En utilisant les connaissances acquises, les méthodes de détection d'anomalies pourraient faire la différence entre un point de données anormal ou normal. Certains des algorithmes non supervisés comme le clustering, KNN peut détecter des anomalies en fonction des données et de ses fonctionnalités.
Apprentissage semi-supervisé
Ces types d'algorithmes ou de méthodes ne sont ni entièrement supervisés ni entièrement non supervisés. Ils se situent essentiellement entre les deux méthodes d'apprentissage supervisé et non supervisé. Ces types d'algorithmes utilisent généralement un petit composant d'apprentissage supervisé, c'est-à-dire une petite quantité de données annotées pré-étiquetées et un grand composant d'apprentissage non supervisé, c'est-à-dire beaucoup de données non étiquetées pour la formation. Nous pouvons suivre l'une des approches suivantes pour mettre en œuvre des méthodes d'apprentissage semi-supervisé -
La première et simple approche consiste à construire le modèle supervisé basé sur une petite quantité de données étiquetées et annotées, puis à construire le modèle non supervisé en appliquant la même chose aux grandes quantités de données non étiquetées pour obtenir plus d'échantillons étiquetés. Maintenant, entraînez le modèle sur eux et répétez le processus.
- , p> La deuxième approche nécessite des efforts supplémentaires. Dans cette approche, nous pouvons d'abord utiliser les méthodes non supervisées pour regrouper des échantillons de données similaires, annoter ces groupes, puis utiliser une combinaison de ces informations pour entraîner le modèle.
Apprentissage par renforcement
Ces méthodes sont différentes des méthodes étudiées précédemment et très rarement utilisées également. Dans ce type d'algorithmes d'apprentissage, il y aurait un agent que nous souhaitons former sur une période de temps afin qu'il puisse interagir avec un environnement spécifique. L'agent suivra un ensemble de stratégies d'interaction avec l'environnement, puis après avoir observé l'environnement, il prendra des mesures concernant l'état actuel de l'environnement. Voici les principales étapes des méthodes d'apprentissage par renforcement -
Step1 - Premièrement, nous devons préparer un agent avec un ensemble initial de stratégies.
Step2 - Observez ensuite l'environnement et son état actuel.
Step3 - Ensuite, sélectionnez la politique optimale concernant l'état actuel de l'environnement et effectuez une action importante.
Step4 - Maintenant, l'agent peut obtenir la récompense ou la pénalité correspondante conformément à l'action qu'il a entreprise à l'étape précédente.
Step5 - Maintenant, nous pouvons mettre à jour les stratégies si cela est nécessaire.
Step6 - Enfin, répétez les étapes 2 à 5 jusqu'à ce que l'agent apprenne et adopte les politiques optimales.
Tâches adaptées à l'apprentissage automatique
Le diagramme suivant montre quel type de tâche est approprié pour divers problèmes de ML -

Basé sur la capacité d'apprentissage
Dans le processus d'apprentissage, voici quelques méthodes basées sur la capacité d'apprentissage -
Batch Learning
Dans de nombreux cas, nous avons des systèmes d'apprentissage automatique de bout en bout dans lesquels nous devons former le modèle en une seule fois en utilisant toutes les données d'entraînement disponibles. Ce type de méthode d'apprentissage ou d'algorithme est appeléBatch or Offline learning. Il est appelé apprentissage par lots ou hors ligne car il s'agit d'une procédure unique et le modèle sera formé avec des données dans un seul lot. Voici les principales étapes des méthodes d'apprentissage par lots -
Step1 - Tout d'abord, nous devons collecter toutes les données d'entraînement pour commencer à entraîner le modèle.
Step2 - Maintenant, commencez la formation du modèle en fournissant des données de formation complètes en une seule fois.
Step3 - Ensuite, arrêtez le processus d'apprentissage / de formation une fois que vous avez obtenu des résultats / performances satisfaisants.
Step4- Enfin, déployez ce modèle entraîné en production. Ici, il prédira la sortie pour un nouvel échantillon de données.
Apprentissage en ligne
C'est complètement opposé aux méthodes d'apprentissage par lots ou hors ligne. Dans ces méthodes d'apprentissage, les données d'apprentissage sont fournies en plusieurs lots incrémentiels, appelés mini-lots, à l'algorithme. Les étapes suivantes sont les principales étapes des méthodes d'apprentissage en ligne -
Step1 - Premièrement, nous devons collecter toutes les données de formation pour commencer la formation du modèle.
Step2 - Maintenant, démarrez l'apprentissage du modèle en fournissant un mini-lot de données d'entraînement à l'algorithme.
Step3 - Ensuite, nous devons fournir les mini-lots de données d'entraînement en plusieurs incréments à l'algorithme.
Step4 - Comme il ne s'arrêtera pas comme l'apprentissage par lots, après avoir fourni des données d'entraînement entières en mini-lots, fournissez également de nouveaux échantillons de données.
Step5 - Enfin, il continuera à apprendre sur une période de temps basée sur les nouveaux échantillons de données.
Basé sur une approche de généralisation
Dans le processus d'apprentissage, voici quelques méthodes basées sur des approches de généralisation -
Apprentissage basé sur une instance
La méthode d'apprentissage basée sur les instances est l'une des méthodes utiles qui construisent les modèles ML en faisant une généralisation basée sur les données d'entrée. C'est le contraire des méthodes d'apprentissage précédemment étudiées dans la mesure où ce type d'apprentissage implique des systèmes d'apprentissage automatique ainsi que des méthodes qui utilisent les points de données brutes eux-mêmes pour tirer les résultats d'échantillons de données plus récents sans construire un modèle explicite sur les données d'apprentissage.
En termes simples, l'apprentissage basé sur des instances commence essentiellement à fonctionner en examinant les points de données d'entrée, puis en utilisant une métrique de similitude, il généralisera et prédira les nouveaux points de données.
Apprentissage basé sur un modèle
Dans les méthodes d'apprentissage basées sur un modèle, un processus itératif a lieu sur les modèles ML qui sont construits en fonction de divers paramètres de modèle, appelés hyperparamètres et dans lesquels les données d'entrée sont utilisées pour extraire les entités. Dans cet apprentissage, les hyperparamètres sont optimisés en fonction de diverses techniques de validation de modèle. C'est pourquoi nous pouvons dire que les méthodes d'apprentissage basées sur des modèles utilisent une approche ML plus traditionnelle vers la généralisation.
Supposons que si vous souhaitez démarrer un projet ML, quelle est la première et la plus importante chose dont vous auriez besoin? Ce sont les données que nous devons charger pour démarrer l'un des projets ML. En ce qui concerne les données, le format de données le plus courant pour les projets ML est CSV (valeurs séparées par des virgules).
Fondamentalement, CSV est un format de fichier simple qui est utilisé pour stocker des données tabulaires (nombre et texte) telles qu'une feuille de calcul en texte brut. En Python, nous pouvons charger des données CSV de différentes manières, mais avant de charger des données CSV, nous devons prendre en compte certaines considérations.
Considérations lors du chargement des données CSV
Le format de données CSV est le format le plus courant pour les données ML, mais nous devons prendre soin de suivre les principales considérations lors de leur chargement dans nos projets ML -
En-tête de fichier
Dans les fichiers de données CSV, l'en-tête contient les informations pour chaque champ. Nous devons utiliser le même délimiteur pour le fichier d'en-tête et pour le fichier de données car c'est le fichier d'en-tête qui spécifie comment les champs de données doivent être interprétés.
Voici les deux cas liés à l'en-tête de fichier CSV qui doivent être pris en compte -
Case-I: When Data file is having a file header - Il attribuera automatiquement les noms à chaque colonne de données si le fichier de données a un en-tête de fichier.
Case-II: When Data file is not having a file header - Nous devons attribuer les noms à chaque colonne de données manuellement si le fichier de données n'a pas d'en-tête de fichier.
Dans les deux cas, nous devons spécifier explicitement si notre fichier CSV contient un en-tête ou non.
commentaires
Les commentaires dans n'importe quel fichier de données ont leur signification. Dans un fichier de données CSV, les commentaires sont indiqués par un hachage (#) au début de la ligne. Nous devons tenir compte des commentaires lors du chargement des données CSV dans les projets ML, car si nous avons des commentaires dans le fichier, nous pouvons avoir besoin d'indiquer, cela dépend de la méthode que nous choisissons pour le chargement, si nous devons attendre ces commentaires ou non.
Délimiteur
Dans les fichiers de données CSV, le caractère virgule (,) est le délimiteur standard. Le rôle du délimiteur est de séparer les valeurs dans les champs. Il est important de prendre en compte le rôle de délimiteur lors du téléchargement du fichier CSV dans les projets ML, car nous pouvons également utiliser un autre délimiteur tel qu'une tabulation ou un espace blanc. Mais dans le cas de l'utilisation d'un délimiteur différent de celui standard, nous devons le spécifier explicitement.
Citations
Dans les fichiers de données CSV, la marque de guillemets doubles («») est le caractère de guillemet par défaut. Il est important de prendre en compte le rôle des guillemets lors du téléchargement du fichier CSV dans les projets ML, car nous pouvons également utiliser un autre caractère de guillemet que les guillemets doubles. Mais en cas d'utilisation d'un caractère guillemet différent du caractère standard, nous devons le spécifier explicitement.
Méthodes de chargement du fichier de données CSV
Lorsque vous travaillez avec des projets ML, la tâche la plus cruciale consiste à y charger correctement les données. Le format de données le plus courant pour les projets ML est CSV et il se présente sous différentes saveurs et différentes difficultés à analyser. Dans cette section, nous allons discuter de trois approches courantes en Python pour charger un fichier de données CSV -
Charger CSV avec la bibliothèque standard Python
La première approche et la plus utilisée pour charger un fichier de données CSV est l'utilisation de la bibliothèque standard Python qui nous fournit une variété de modules intégrés, à savoir le module csv et la fonction reader (). Ce qui suit est un exemple de chargement de fichier de données CSV à l'aide de celui-ci -
Exemple
Dans cet exemple, nous utilisons l'ensemble de données de fleurs d'iris qui peut être téléchargé dans notre répertoire local. Après avoir chargé le fichier de données, nous pouvons le convertir en tableau NumPy et l'utiliser pour les projets ML. Voici le script Python pour charger le fichier de données CSV -
Tout d'abord, nous devons importer le module csv fourni par la bibliothèque standard Python comme suit -
import csvEnsuite, nous devons importer le module Numpy pour convertir les données chargées en tableau NumPy.
import numpy as npMaintenant, fournissez le chemin complet du fichier, stocké sur notre répertoire local, ayant le fichier de données CSV -
path = r"c:\iris.csv"Ensuite, utilisez la fonction csv.reader () pour lire les données du fichier CSV -
with open(path,'r') as f:
reader = csv.reader(f,delimiter = ',')
headers = next(reader)
data = list(reader)
data = np.array(data).astype(float)Nous pouvons imprimer les noms des en-têtes avec la ligne de script suivante -
print(headers)La ligne de script suivante imprimera la forme des données, c'est-à-dire le nombre de lignes et de colonnes dans le fichier -
print(data.shape)La ligne de script suivante donnera les trois premières lignes du fichier de données -
print(data[:3])Output
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
(150, 4)
[ [5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]]Charger CSV avec NumPy
Une autre approche pour charger un fichier de données CSV est la fonction NumPy et numpy.loadtxt (). Ce qui suit est un exemple de chargement de fichier de données CSV à l'aide de celui-ci -
Exemple
Dans cet exemple, nous utilisons l'ensemble de données des Indiens Pima contenant les données des patients diabétiques. Cet ensemble de données est un ensemble de données numériques sans en-tête. Il peut également être téléchargé dans notre répertoire local. Après avoir chargé le fichier de données, nous pouvons le convertir en tableau NumPy et l'utiliser pour les projets ML. Voici le script Python pour charger le fichier de données CSV -
from numpy import loadtxt
path = r"C:\pima-indians-diabetes.csv"
datapath= open(path, 'r')
data = loadtxt(datapath, delimiter=",")
print(data.shape)
print(data[:3])Production
(768, 9)
[ [ 6. 148. 72. 35. 0. 33.6 0.627 50. 1.]
[ 1. 85. 66. 29. 0. 26.6 0.351 31. 0.]
[ 8. 183. 64. 0. 0. 23.3 0.672 32. 1.]]Charger CSV avec Pandas
Une autre approche pour charger un fichier de données CSV consiste à utiliser la fonction Pandas et pandas.read_csv (). C'est la fonction très flexible qui renvoie un pandas.DataFrame qui peut être utilisé immédiatement pour le traçage. Ce qui suit est un exemple de chargement de fichier de données CSV à l'aide de celui-ci -
Exemple
Ici, nous allons implémenter deux scripts Python, le premier est avec l'ensemble de données Iris ayant des en-têtes et un autre en utilisant le jeu de données Pima Indians qui est un ensemble de données numériques sans en-tête. Les deux ensembles de données peuvent être téléchargés dans le répertoire local.
Script-1
Voici le script Python pour charger le fichier de données CSV à l'aide de Pandas sur l'ensemble de données Iris -
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)
print(data[:3])
Output:
(150, 4)
sepal_length sepal_width petal_length petal_width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2Script-2
Ce qui suit est le script Python pour charger le fichier de données CSV, ainsi que pour fournir les noms des en-têtes, en utilisant l'ensemble de données Pandas sur Pima Indians Diabetes -
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.shape)
print(data[:3])Output
(768, 9)
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1La différence entre les trois approches utilisées ci-dessus pour charger le fichier de données CSV peut être facilement comprise à l'aide d'exemples donnés.
introduction
Lorsque nous travaillons avec des projets d'apprentissage automatique, nous ignorons généralement deux parties les plus importantes appelées mathematics et data. C'est parce que nous savons que le ML est une approche basée sur les données et que notre modèle de ML ne produira que des résultats aussi bons ou aussi mauvais que les données que nous lui avons fournies.
Dans le chapitre précédent, nous avons discuté de la façon dont nous pouvons télécharger des données CSV dans notre projet ML, mais il serait bon de comprendre les données avant de les télécharger. Nous pouvons comprendre les données de deux manières, avec des statistiques et avec une visualisation.
Dans ce chapitre, à l'aide des recettes Python suivantes, nous allons comprendre les données ML avec des statistiques.
Examen des données brutes
La toute première recette consiste à examiner vos données brutes. Il est important d'examiner les données brutes, car les informations que nous obtiendrons après avoir examiné les données brutes augmenteront nos chances d'améliorer le prétraitement et le traitement des données pour les projets ML.
Voici un script Python implémenté à l'aide de la fonction head () de Pandas DataFrame sur l'ensemble de données sur le diabète des Indiens Pima pour examiner les 50 premières lignes pour mieux le comprendre -
Exemple
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.head(50))Production
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1
5 5 116 74 0 0 25.6 0.201 30 0
6 3 78 50 32 88 31.0 0.248 26 1
7 10 115 0 0 0 35.3 0.134 29 0
8 2 197 70 45 543 30.5 0.158 53 1
9 8 125 96 0 0 0.0 0.232 54 1
10 4 110 92 0 0 37.6 0.191 30 0
11 10 168 74 0 0 38.0 0.537 34 1
12 10 139 80 0 0 27.1 1.441 57 0
13 1 189 60 23 846 30.1 0.398 59 1
14 5 166 72 19 175 25.8 0.587 51 1
15 7 100 0 0 0 30.0 0.484 32 1
16 0 118 84 47 230 45.8 0.551 31 1
17 7 107 74 0 0 29.6 0.254 31 1
18 1 103 30 38 83 43.3 0.183 33 0
19 1 115 70 30 96 34.6 0.529 32 1
20 3 126 88 41 235 39.3 0.704 27 0
21 8 99 84 0 0 35.4 0.388 50 0
22 7 196 90 0 0 39.8 0.451 41 1
23 9 119 80 35 0 29.0 0.263 29 1
24 11 143 94 33 146 36.6 0.254 51 1
25 10 125 70 26 115 31.1 0.205 41 1
26 7 147 76 0 0 39.4 0.257 43 1
27 1 97 66 15 140 23.2 0.487 22 0
28 13 145 82 19 110 22.2 0.245 57 0
29 5 117 92 0 0 34.1 0.337 38 0
30 5 109 75 26 0 36.0 0.546 60 0
31 3 158 76 36 245 31.6 0.851 28 1
32 3 88 58 11 54 24.8 0.267 22 0
33 6 92 92 0 0 19.9 0.188 28 0
34 10 122 78 31 0 27.6 0.512 45 0
35 4 103 60 33 192 24.0 0.966 33 0
36 11 138 76 0 0 33.2 0.420 35 0
37 9 102 76 37 0 32.9 0.665 46 1
38 2 90 68 42 0 38.2 0.503 27 1
39 4 111 72 47 207 37.1 1.390 56 1
40 3 180 64 25 70 34.0 0.271 26 0
41 7 133 84 0 0 40.2 0.696 37 0
42 7 106 92 18 0 22.7 0.235 48 0
43 9 171 110 24 240 45.4 0.721 54 1
44 7 159 64 0 0 27.4 0.294 40 0
45 0 180 66 39 0 42.0 1.893 25 1
46 1 146 56 0 0 29.7 0.564 29 0
47 2 71 70 27 0 28.0 0.586 22 0
48 7 103 66 32 0 39.1 0.344 31 1
49 7 105 0 0 0 0.0 0.305 24 0Nous pouvons observer à partir de la sortie ci-dessus que la première colonne donne le numéro de ligne qui peut être très utile pour référencer une observation spécifique.
Vérification des dimensions des données
C'est toujours une bonne pratique de savoir combien de données, en termes de lignes et de colonnes, nous avons pour notre projet ML. Les raisons derrière sont -
Supposons que si nous avons trop de lignes et de colonnes, il faudrait beaucoup de temps pour exécuter l'algorithme et entraîner le modèle.
Supposons que si nous avons trop moins de lignes et de colonnes, nous n'aurions pas assez de données pour bien entraîner le modèle.
Voici un script Python implémenté en imprimant la propriété shape sur Pandas Data Frame. Nous allons l'implémenter sur l'ensemble de données d'iris pour obtenir le nombre total de lignes et de colonnes qu'il contient.
Exemple
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)Production
(150, 4)Nous pouvons facilement observer à partir de la sortie que l'ensemble de données d'iris, que nous allons utiliser, comporte 150 lignes et 4 colonnes.
Obtenir le type de données de chaque attribut
Connaître le type de données de chaque attribut est une autre bonne pratique. La raison en est que, conformément à l'exigence, nous pouvons parfois avoir besoin de convertir un type de données en un autre. Par exemple, nous pouvons avoir besoin de convertir une chaîne en virgule flottante ou en entier pour représenter des valeurs catégorielles ou ordinales. Nous pouvons avoir une idée du type de données de l'attribut en regardant les données brutes, mais une autre façon consiste à utiliser la propriété dtypes de Pandas DataFrame. Avec l'aide de la propriété dtypes, nous pouvons catégoriser chaque type de données d'attributs. Cela peut être compris à l'aide du script Python suivant -
Exemple
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.dtypes)Production
sepal_length float64
sepal_width float64
petal_length float64
petal_width float64
dtype: objectÀ partir de la sortie ci-dessus, nous pouvons facilement obtenir les types de données de chaque attribut.
Résumé statistique des données
Nous avons discuté de la recette Python pour obtenir la forme, c'est-à-dire le nombre de lignes et de colonnes, de données, mais nous devons souvent revoir les résumés de cette forme de données. Cela peut être fait à l'aide de la fonction describe () de Pandas DataFrame qui fournit en outre les 8 propriétés statistiques suivantes de chaque attribut de données -
Count
Mean
Écart-type
Valeur minimum
Valeur maximum
25%
Médiane soit 50%
75%
Exemple
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
print(data.shape)
print(data.describe())Production
(768, 9)
preg plas pres skin test mass pedi age class
count 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00
mean 3.85 120.89 69.11 20.54 79.80 31.99 0.47 33.24 0.35
std 3.37 31.97 19.36 15.95 115.24 7.88 0.33 11.76 0.48
min 0.00 0.00 0.00 0.00 0.00 0.00 0.08 21.00 0.00
25% 1.00 99.00 62.00 0.00 0.00 27.30 0.24 24.00 0.00
50% 3.00 117.00 72.00 23.00 30.50 32.00 0.37 29.00 0.00
75% 6.00 140.25 80.00 32.00 127.25 36.60 0.63 41.00 1.00
max 17.00 199.00 122.00 99.00 846.00 67.10 2.42 81.00 1.00À partir de la sortie ci-dessus, nous pouvons observer le résumé statistique des données de l'ensemble de données Pima Indian Diabetes ainsi que la forme des données.
Révision de la distribution des classes
Les statistiques de distribution de classe sont utiles dans les problèmes de classification où nous avons besoin de connaître l'équilibre des valeurs de classe. Il est important de connaître la distribution des valeurs de classe car si nous avons une distribution de classe très déséquilibrée, c'est-à-dire qu'une classe a beaucoup plus d'observations qu'une autre classe, elle peut nécessiter un traitement spécial au stade de la préparation des données de notre projet ML. Nous pouvons facilement obtenir une distribution de classe en Python avec l'aide de Pandas DataFrame.
Exemple
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
count_class = data.groupby('class').size()
print(count_class)Production
Class
0 500
1 268
dtype: int64À partir du résultat ci-dessus, on peut clairement voir que le nombre d'observations avec la classe 0 est presque le double du nombre d'observations avec la classe 1.
Examen de la corrélation entre les attributs
La relation entre deux variables est appelée corrélation. En statistique, la méthode la plus courante pour calculer la corrélation est le coefficient de corrélation de Pearson. Il peut avoir trois valeurs comme suit -
Coefficient value = 1 - Il représente plein positive corrélation entre les variables.
Coefficient value = -1 - Il représente plein negative corrélation entre les variables.
Coefficient value = 0 - Il représente no corrélation du tout entre les variables.
Il est toujours bon pour nous de passer en revue les corrélations par paires des attributs de notre ensemble de données avant de les utiliser dans un projet ML, car certains algorithmes d'apprentissage automatique tels que la régression linéaire et la régression logistique fonctionneront mal si nous avons des attributs hautement corrélés. En Python, nous pouvons facilement calculer une matrice de corrélation des attributs de jeu de données à l'aide de la fonction corr () sur Pandas DataFrame.
Exemple
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
correlations = data.corr(method='pearson')
print(correlations)Production
preg plas pres skin test mass pedi age class
preg 1.00 0.13 0.14 -0.08 -0.07 0.02 -0.03 0.54 0.22
plas 0.13 1.00 0.15 0.06 0.33 0.22 0.14 0.26 0.47
pres 0.14 0.15 1.00 0.21 0.09 0.28 0.04 0.24 0.07
skin -0.08 0.06 0.21 1.00 0.44 0.39 0.18 -0.11 0.07
test -0.07 0.33 0.09 0.44 1.00 0.20 0.19 -0.04 0.13
mass 0.02 0.22 0.28 0.39 0.20 1.00 0.14 0.04 0.29
pedi -0.03 0.14 0.04 0.18 0.19 0.14 1.00 0.03 0.17
age 0.54 0.26 0.24 -0.11 -0.04 0.04 0.03 1.00 0.24
class 0.22 0.47 0.07 0.07 0.13 0.29 0.17 0.24 1.00La matrice dans la sortie ci-dessus donne la corrélation entre toutes les paires de l'attribut dans l'ensemble de données.
Examen de l'inclinaison de la distribution des attributs
L'asymétrie peut être définie comme la distribution supposée gaussienne mais qui semble déformée ou décalée dans un sens ou dans l'autre, ou vers la gauche ou vers la droite. L'examen de l'asymétrie des attributs est l'une des tâches importantes pour les raisons suivantes -
La présence d'asymétrie dans les données nécessite la correction au stade de la préparation des données afin que nous puissions obtenir plus de précision de notre modèle.
La plupart des algorithmes ML supposent que les données ont une distribution gaussienne, c'est-à-dire soit la normale des données courbes en cloche.
En Python, nous pouvons facilement calculer l'inclinaison de chaque attribut en utilisant la fonction skew () sur Pandas DataFrame.
Exemple
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
print(data.skew())Production
preg 0.90
plas 0.17
pres -1.84
skin 0.11
test 2.27
mass -0.43
pedi 1.92
age 1.13
class 0.64
dtype: float64À partir de la sortie ci-dessus, un biais positif ou négatif peut être observé. Si la valeur est plus proche de zéro, cela montre moins de biais.
introduction
Dans le chapitre précédent, nous avons discuté de l'importance des données pour les algorithmes d'apprentissage automatique ainsi que de certaines recettes Python pour comprendre les données avec des statistiques. Il existe un autre moyen appelé Visualisation, pour comprendre les données.
À l'aide de la visualisation des données, nous pouvons voir à quoi ressemblent les données et quel type de corrélation est détenu par les attributs des données. C'est le moyen le plus rapide de voir si les fonctionnalités correspondent à la sortie. Avec l'aide des recettes Python suivantes, nous pouvons comprendre les données ML avec des statistiques.

Graphiques univariés: comprendre les attributs indépendamment
Le type de visualisation le plus simple est la visualisation à variable unique ou «univariée». Avec l'aide de la visualisation univariée, nous pouvons comprendre chaque attribut de notre ensemble de données indépendamment. Voici quelques techniques en Python pour implémenter la visualisation univariée -
Histogrammes
Les histogrammes regroupent les données dans des bacs et constituent le moyen le plus rapide de se faire une idée de la distribution de chaque attribut dans l'ensemble de données. Voici quelques-unes des caractéristiques des histogrammes -
Il nous fournit un décompte du nombre d'observations dans chaque bac créé pour la visualisation.
A partir de la forme du bac, on peut facilement observer la distribution c'est-à-dire qu'il est gaussien, asymétrique ou exponentiel.
Les histogrammes nous aident également à voir les valeurs aberrantes possibles.
Exemple
Le code ci-dessous est un exemple de script Python créant l'histogramme des attributs de l'ensemble de données Pima Indian Diabetes. Ici, nous utiliserons la fonction hist () sur Pandas DataFrame pour générer des histogrammes etmatplotlib pour les tracer.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.hist()
pyplot.show()Production
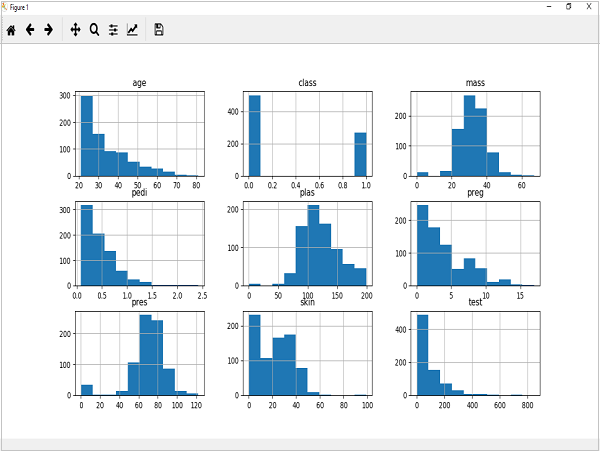
La sortie ci-dessus montre qu'elle a créé l'histogramme pour chaque attribut de l'ensemble de données. À partir de là, nous pouvons observer que peut-être l'âge, le pedi et l'attribut de test peuvent avoir une distribution exponentielle tandis que la masse et les plas ont une distribution gaussienne.
Tracés de densité
Les graphiques de densité sont une autre technique simple et rapide pour obtenir chaque distribution d'attributs. C'est aussi comme un histogramme mais avec une courbe lisse dessinée à travers le haut de chaque bac. Nous pouvons les appeler des histogrammes abstraits.
Exemple
Dans l'exemple suivant, le script Python générera des diagrammes de densité pour la distribution des attributs de l'ensemble de données Pima Indian Diabetes.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='density', subplots=True, layout=(3,3), sharex=False)
pyplot.show()Production
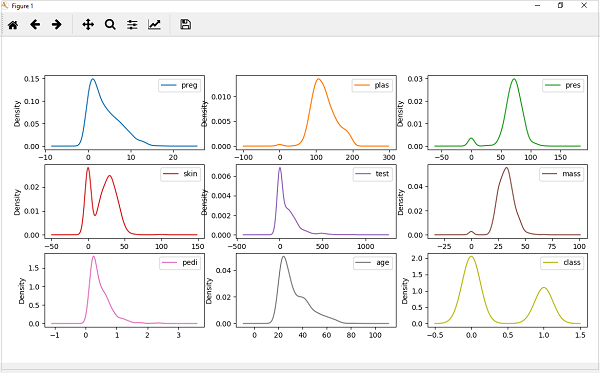
À partir de la sortie ci-dessus, la différence entre les graphiques de densité et les histogrammes peut être facilement comprise.
Tracés en boîte et moustaches
Les diagrammes en boîte et en moustache, également appelés boîtes à moustaches, sont une autre technique utile pour examiner la distribution de la distribution de chaque attribut. Voici les caractéristiques de cette technique -
Il est de nature univariée et résume la distribution de chaque attribut.
Il trace une ligne pour la valeur médiane, c'est-à-dire pour la médiane.
Il dessine une boîte autour des 25% et 75%.
Il dessine également des moustaches qui nous donneront une idée de la diffusion des données.
Les points à l'extérieur des moustaches indiquent les valeurs aberrantes. Les valeurs aberrantes seraient 1,5 fois supérieures à la taille de la dispersion des données intermédiaires.
Exemple
Dans l'exemple suivant, le script Python générera des diagrammes de densité pour la distribution des attributs de l'ensemble de données Pima Indian Diabetes.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False)
pyplot.show()Production

À partir du graphique ci-dessus de la distribution des attributs, on peut observer que l'âge, le test et la peau semblent biaisés vers des valeurs plus petites.
Graphiques multivariés: interaction entre plusieurs variables
Un autre type de visualisation est la visualisation à plusieurs variables ou «multivariée». À l'aide de la visualisation multivariée, nous pouvons comprendre l'interaction entre plusieurs attributs de notre ensemble de données. Voici quelques techniques en Python pour implémenter la visualisation multivariée -
Diagramme de matrice de corrélation
La corrélation est une indication des changements entre deux variables. Dans nos chapitres précédents, nous avons discuté des coefficients de corrélation de Pearson et de l'importance de la corrélation également. Nous pouvons tracer une matrice de corrélation pour montrer quelle variable a une corrélation élevée ou faible par rapport à une autre variable.
Exemple
Dans l'exemple suivant, le script Python générera et tracera une matrice de corrélation pour l'ensemble de données Pima Indian Diabetes. Il peut être généré à l'aide de la fonction corr () sur Pandas DataFrame et tracé à l'aide de pyplot.
from matplotlib import pyplot
from pandas import read_csv
import numpy
Path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(Path, names=names)
correlations = data.corr()
fig = pyplot.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(correlations, vmin=-1, vmax=1)
fig.colorbar(cax)
ticks = numpy.arange(0,9,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
pyplot.show()Production

À partir de la sortie ci-dessus de la matrice de corrélation, nous pouvons voir qu'elle est symétrique, c'est-à-dire que la partie inférieure gauche est la même que la partie supérieure droite. On observe également que chaque variable est positivement corrélée entre elles.
Diagramme de matrice de dispersion
Les nuages de points montrent dans quelle mesure une variable est affectée par une autre ou la relation entre elles à l'aide de points en deux dimensions. Les nuages de points ressemblent beaucoup aux graphiques linéaires dans la mesure où ils utilisent des axes horizontaux et verticaux pour tracer des points de données.
Exemple
Dans l'exemple suivant, le script Python générera et tracera la matrice Scatter pour l'ensemble de données Pima Indian Diabetes. Il peut être généré à l'aide de la fonction scatter_matrix () sur Pandas DataFrame et tracé à l'aide de pyplot.
from matplotlib import pyplot
from pandas import read_csv
from pandas.tools.plotting import scatter_matrix
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
scatter_matrix(data)
pyplot.show()Production

introduction
Les algorithmes d'apprentissage automatique sont complètement dépendants des données car c'est l'aspect le plus crucial qui rend possible l'apprentissage des modèles. D'un autre côté, si nous ne pouvons pas donner un sens à ces données, avant de les alimenter en algorithmes ML, une machine sera inutile. En termes simples, nous devons toujours fournir les bonnes données, c'est-à-dire les données à l'échelle, au format et aux caractéristiques significatives, pour le problème que nous voulons que la machine résolve.
Cela fait de la préparation des données l'étape la plus importante du processus de ML. La préparation des données peut être définie comme la procédure qui rend notre ensemble de données plus approprié pour le processus de ML.
Pourquoi le prétraitement des données?
Après avoir sélectionné les données brutes pour la formation ML, la tâche la plus importante est le prétraitement des données. Au sens large, le prétraitement des données convertira les données sélectionnées dans une forme avec laquelle nous pouvons travailler ou alimenter des algorithmes ML. Nous devons toujours prétraiter nos données afin qu'elles soient conformes aux attentes de l'algorithme d'apprentissage automatique.
Techniques de prétraitement des données
Nous avons les techniques de prétraitement des données suivantes qui peuvent être appliquées sur un ensemble de données pour produire des données pour les algorithmes ML -
Mise à l'échelle
Très probablement, notre ensemble de données comprend des attributs avec une échelle variable, mais nous ne pouvons pas fournir de telles données à l'algorithme ML, par conséquent, il nécessite un redimensionnement. La remise à l'échelle des données garantit que les attributs sont à la même échelle. En général, les attributs sont redimensionnés dans la plage de 0 et 1. Les algorithmes ML tels que la descente de gradient et les k-voisins les plus proches nécessitent des données mises à l'échelle. Nous pouvons redimensionner les données à l'aide de la classe MinMaxScaler de la bibliothèque Python scikit-learn.
Exemple
Dans cet exemple, nous redimensionnerons les données de l'ensemble de données Pima Indians Diabetes que nous avons utilisé précédemment. Tout d'abord, les données CSV seront chargées (comme cela a été fait dans les chapitres précédents), puis à l'aide de la classe MinMaxScaler, elles seront redimensionnées dans la plage de 0 et 1.
Les premières lignes du script suivant sont les mêmes que celles que nous avons écrites dans les chapitres précédents lors du chargement des données CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn import preprocessing
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesMaintenant, nous pouvons utiliser la classe MinMaxScaler pour redimensionner les données dans la plage de 0 et 1.
data_scaler = preprocessing.MinMaxScaler(feature_range=(0,1))
data_rescaled = data_scaler.fit_transform(array)Nous pouvons également résumer les données pour la sortie selon notre choix. Ici, nous définissons la précision sur 1 et affichons les 10 premières lignes dans la sortie.
set_printoptions(precision=1)
print ("\nScaled data:\n", data_rescaled[0:10])Production
Scaled data:
[[0.4 0.7 0.6 0.4 0. 0.5 0.2 0.5 1. ]
[0.1 0.4 0.5 0.3 0. 0.4 0.1 0.2 0. ]
[0.5 0.9 0.5 0. 0. 0.3 0.3 0.2 1. ]
[0.1 0.4 0.5 0.2 0.1 0.4 0. 0. 0. ]
[0. 0.7 0.3 0.4 0.2 0.6 0.9 0.2 1. ]
[0.3 0.6 0.6 0. 0. 0.4 0.1 0.2 0. ]
[0.2 0.4 0.4 0.3 0.1 0.5 0.1 0.1 1. ]
[0.6 0.6 0. 0. 0. 0.5 0. 0.1 0. ]
[0.1 1. 0.6 0.5 0.6 0.5 0. 0.5 1. ]
[0.5 0.6 0.8 0. 0. 0. 0.1 0.6 1. ]]À partir de la sortie ci-dessus, toutes les données ont été redimensionnées dans la plage de 0 et 1.
Normalisation
La normalisation est une autre technique de prétraitement des données utile. Ceci est utilisé pour redimensionner chaque ligne de données pour avoir une longueur de 1. C'est principalement utile dans le jeu de données Sparse où nous avons beaucoup de zéros. Nous pouvons redimensionner les données à l'aide de la classe Normalizer de la bibliothèque Python scikit-learn.
Types de normalisation
Dans l'apprentissage automatique, il existe deux types de techniques de prétraitement de normalisation:
Normalisation L1
Elle peut être définie comme la technique de normalisation qui modifie les valeurs de l'ensemble de données de telle sorte que dans chaque ligne, la somme des valeurs absolues sera toujours jusqu'à 1. Elle est également appelée écarts les moins absolus.
Example
Dans cet exemple, nous utilisons la technique de normalisation L1 pour normaliser les données de l'ensemble de données Pima Indians Diabetes que nous avons utilisé précédemment. Tout d'abord, les données CSV seront chargées, puis à l'aide de la classe Normalizer, elles seront normalisées.
Les premières lignes du script suivant sont les mêmes que celles que nous avons écrites dans les chapitres précédents lors du chargement des données CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesMaintenant, nous pouvons utiliser la classe Normalizer avec L1 pour normaliser les données.
Data_normalizer = Normalizer(norm='l1').fit(array)
Data_normalized = Data_normalizer.transform(array)Nous pouvons également résumer les données pour la sortie selon notre choix. Ici, nous définissons la précision sur 2 et affichons les 3 premières lignes dans la sortie.
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.02 0.43 0.21 0.1 0. 0.1 0. 0.14 0. ]
[0. 0.36 0.28 0.12 0. 0.11 0. 0.13 0. ]
[0.03 0.59 0.21 0. 0. 0.07 0. 0.1 0. ]]Normalisation L2
Elle peut être définie comme la technique de normalisation qui modifie les valeurs de l'ensemble de données de telle sorte que dans chaque ligne, la somme des carrés sera toujours jusqu'à 1. Elle est également appelée moindres carrés.
Example
Dans cet exemple, nous utilisons la technique de normalisation L2 pour normaliser les données de l'ensemble de données Pima Indians Diabetes que nous avons utilisé précédemment. Tout d'abord, les données CSV seront chargées (comme cela a été fait dans les chapitres précédents), puis à l'aide de la classe Normalizer, elles seront normalisées.
Les premières lignes du script suivant sont les mêmes que celles que nous avons écrites dans les chapitres précédents lors du chargement des données CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesMaintenant, nous pouvons utiliser la classe Normalizer avec L1 pour normaliser les données.
Data_normalizer = Normalizer(norm='l2').fit(array)
Data_normalized = Data_normalizer.transform(array)Nous pouvons également résumer les données pour la sortie selon notre choix. Ici, nous définissons la précision sur 2 et affichons les 3 premières lignes dans la sortie.
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.03 0.83 0.4 0.2 0. 0.19 0. 0.28 0.01]
[0.01 0.72 0.56 0.24 0. 0.22 0. 0.26 0. ]
[0.04 0.92 0.32 0. 0. 0.12 0. 0.16 0.01]]Binarisation
Comme son nom l'indique, c'est la technique à l'aide de laquelle nous pouvons rendre nos données binaires. Nous pouvons utiliser un seuil binaire pour rendre nos données binaires. Les valeurs au-dessus de cette valeur de seuil seront converties en 1 et en dessous de ce seuil seront converties en 0. Par exemple, si nous choisissons la valeur de seuil = 0,5, alors la valeur de l'ensemble de données au-dessus deviendra 1 et en dessous de cela deviendra 0. C'est-à-dire pourquoi on peut l'appelerbinarizing les données ou thresholdingles données. Cette technique est utile lorsque nous avons des probabilités dans notre ensemble de données et que nous voulons les convertir en valeurs nettes.
Nous pouvons binariser les données à l'aide de la classe Binarizer de la bibliothèque Python scikit-learn.
Exemple
Dans cet exemple, nous redimensionnerons les données de l'ensemble de données Pima Indians Diabetes que nous avons utilisé précédemment. Tout d'abord, les données CSV seront chargées, puis à l'aide de la classe Binarizer, elles seront converties en valeurs binaires, c'est-à-dire 0 et 1 en fonction de la valeur de seuil. Nous prenons 0,5 comme valeur seuil.
Les premières lignes du script suivant sont les mêmes que celles que nous avons écrites dans les chapitres précédents lors du chargement des données CSV.
from pandas import read_csv
from sklearn.preprocessing import Binarizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesMaintenant, nous pouvons utiliser la classe Binarize pour convertir les données en valeurs binaires.
binarizer = Binarizer(threshold=0.5).fit(array)
Data_binarized = binarizer.transform(array)Ici, nous montrons les 5 premières lignes de la sortie.
print ("\nBinary data:\n", Data_binarized [0:5])Production
Binary data:
[[1. 1. 1. 1. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 0. 1. 0. 1. 0.]
[1. 1. 1. 0. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 0. 1. 0.]
[0. 1. 1. 1. 1. 1. 1. 1. 1.]]Standardisation
Une autre technique de prétraitement de données utile qui est essentiellement utilisée pour transformer les attributs de données avec une distribution gaussienne. Elle diffère la moyenne et l'écart-type (écart-type) d'une distribution gaussienne standard avec une moyenne de 0 et un écart-type de 1. Cette technique est utile dans les algorithmes ML comme la régression linéaire, la régression logistique qui suppose une distribution gaussienne dans l'ensemble de données d'entrée et produit mieux résultats avec des données redimensionnées. Nous pouvons standardiser les données (moyenne = 0 et SD = 1) à l'aide de la classe StandardScaler de la bibliothèque Python scikit-learn.
Exemple
Dans cet exemple, nous redimensionnerons les données de l'ensemble de données Pima Indians Diabetes que nous avons utilisé précédemment. Tout d'abord, les données CSV seront chargées, puis à l'aide de la classe StandardScaler, elles seront converties en distribution gaussienne avec moyenne = 0 et SD = 1.
Les premières lignes du script suivant sont les mêmes que celles que nous avons écrites dans les chapitres précédents lors du chargement des données CSV.
from sklearn.preprocessing import StandardScaler
from pandas import read_csv
from numpy import set_printoptions
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesMaintenant, nous pouvons utiliser la classe StandardScaler pour redimensionner les données.
data_scaler = StandardScaler().fit(array)
data_rescaled = data_scaler.transform(array)Nous pouvons également résumer les données pour la sortie selon notre choix. Ici, nous définissons la précision sur 2 et affichons les 5 premières lignes dans la sortie.
set_printoptions(precision=2)
print ("\nRescaled data:\n", data_rescaled [0:5])Production
Rescaled data:
[[ 0.64 0.85 0.15 0.91 -0.69 0.2 0.47 1.43 1.37]
[-0.84 -1.12 -0.16 0.53 -0.69 -0.68 -0.37 -0.19 -0.73]
[ 1.23 1.94 -0.26 -1.29 -0.69 -1.1 0.6 -0.11 1.37]
[-0.84 -1. -0.16 0.15 0.12 -0.49 -0.92 -1.04 -0.73]
[-1.14 0.5 -1.5 0.91 0.77 1.41 5.48 -0.02 1.37]]Étiquetage des données
Nous avons discuté de l'importance de bonnes données pour les algorithmes de ML ainsi que de certaines techniques pour prétraiter les données avant de les envoyer aux algorithmes de ML. Un autre aspect à cet égard est l'étiquetage des données. Il est également très important d'envoyer les données à des algorithmes de ML ayant un étiquetage approprié. Par exemple, en cas de problèmes de classification, de nombreuses étiquettes sous forme de mots, de nombres, etc. sont présentes sur les données.
Qu'est-ce que l'encodage d'étiquettes?
La plupart des fonctions sklearn s'attendent à ce que les données portent des étiquettes numériques plutôt que des étiquettes de mots. Par conséquent, nous devons convertir ces étiquettes en étiquettes numériques. Ce processus est appelé encodage d'étiquettes. Nous pouvons effectuer le codage d'étiquettes des données à l'aide de la fonction LabelEncoder () de la bibliothèque Python scikit-learn.
Exemple
Dans l'exemple suivant, le script Python effectuera le codage de l'étiquette.
Tout d'abord, importez les bibliothèques Python requises comme suit -
import numpy as np
from sklearn import preprocessingMaintenant, nous devons fournir les étiquettes d'entrée comme suit -
input_labels = ['red','black','red','green','black','yellow','white']La prochaine ligne de code créera l'encodeur d'étiquette et l'entraînera.
encoder = preprocessing.LabelEncoder()
encoder.fit(input_labels)Les prochaines lignes de script vérifieront les performances en encodant la liste ordonnée au hasard -
test_labels = ['green','red','black']
encoded_values = encoder.transform(test_labels)
print("\nLabels =", test_labels)
print("Encoded values =", list(encoded_values))
encoded_values = [3,0,4,1]
decoded_list = encoder.inverse_transform(encoded_values)Nous pouvons obtenir la liste des valeurs encodées à l'aide du script python suivant -
print("\nEncoded values =", encoded_values)
print("\nDecoded labels =", list(decoded_list))Production
Labels = ['green', 'red', 'black']
Encoded values = [1, 2, 0]
Encoded values = [3, 0, 4, 1]
Decoded labels = ['white', 'black', 'yellow', 'green']Dans le chapitre précédent, nous avons vu en détail comment prétraiter et préparer les données pour l'apprentissage automatique. Dans ce chapitre, laissez-nous comprendre en détail la sélection des caractéristiques des données et les divers aspects qui y sont impliqués.
Importance de la sélection des fonctionnalités de données
Les performances du modèle d'apprentissage automatique sont directement proportionnelles aux fonctionnalités de données utilisées pour l'entraîner. Les performances du modèle ML seront affectées négativement si les fonctionnalités de données qui lui sont fournies ne sont pas pertinentes. D'autre part, l'utilisation de fonctionnalités de données pertinentes peut augmenter la précision de votre modèle ML, en particulier la régression linéaire et logistique.
Maintenant, la question se pose: qu'est-ce que la sélection automatique des fonctionnalités? Il peut être défini comme le processus à l'aide duquel nous sélectionnons les caractéristiques de nos données qui sont les plus pertinentes pour la variable de sortie ou de prédiction qui nous intéresse. Cela s'appelle également la sélection d'attributs.
Voici quelques-uns des avantages de la sélection automatique des fonctionnalités avant de modéliser les données:
La sélection de caractéristiques avant la modélisation des données réduira le surajustement.
La sélection des fonctionnalités avant la modélisation des données augmentera la précision du modèle ML.
La sélection des fonctionnalités avant la modélisation des données réduira le temps de formation
Techniques de sélection des fonctionnalités
Les techniques suivantes sont des techniques de sélection automatique de fonctionnalités que nous pouvons utiliser pour modéliser des données ML en Python -
Sélection univariée
Cette technique de sélection de caractéristiques est très utile pour sélectionner ces caractéristiques, à l'aide de tests statistiques, ayant la relation la plus forte avec les variables de prédiction. Nous pouvons implémenter une technique de sélection de fonctionnalités univariée à l'aide de SelectKBest0class de la bibliothèque Python scikit-learn.
Example
Dans cet exemple, nous utiliserons l'ensemble de données Pima Indians Diabetes pour sélectionner 4 des attributs ayant les meilleures caractéristiques à l'aide du test statistique du chi carré.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesEnsuite, nous séparerons le tableau en composants d'entrée et de sortie -
X = array[:,0:8]
Y = array[:,8]Les lignes de code suivantes sélectionneront les meilleures fonctionnalités de l'ensemble de données -
test = SelectKBest(score_func=chi2, k=4)
fit = test.fit(X,Y)Nous pouvons également résumer les données pour la sortie selon notre choix. Ici, nous définissons la précision sur 2 et montrons les 4 attributs de données avec les meilleures caractéristiques ainsi que le meilleur score de chaque attribut -
set_printoptions(precision=2)
print(fit.scores_)
featured_data = fit.transform(X)
print ("\nFeatured data:\n", featured_data[0:4])Output
[ 111.52 1411.89 17.61 53.11 2175.57 127.67 5.39 181.3 ]
Featured data:
[[148. 0. 33.6 50. ]
[ 85. 0. 26.6 31. ]
[183. 0. 23.3 32. ]
[ 89. 94. 28.1 21. ]]Élimination des caractéristiques récursives
Comme son nom l'indique, la technique de sélection des caractéristiques RFE (élimination des caractéristiques récursives) supprime les attributs de manière récursive et construit le modèle avec les attributs restants. Nous pouvons implémenter la technique de sélection des fonctionnalités RFE à l'aide de la classe RFE de la bibliothèque Python scikit-learn.
Exemple
Dans cet exemple, nous utiliserons RFE avec un algorithme de régression logistique pour sélectionner les 3 meilleurs attributs ayant les meilleures caractéristiques de l'ensemble de données Pima Indians Diabetes à.
from pandas import read_csv
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesEnsuite, nous allons séparer le tableau en ses composants d'entrée et de sortie -
X = array[:,0:8]
Y = array[:,8]Les lignes de code suivantes sélectionneront les meilleures fonctionnalités d'un ensemble de données -
model = LogisticRegression()
rfe = RFE(model, 3)
fit = rfe.fit(X, Y)
print("Number of Features: %d")
print("Selected Features: %s")
print("Feature Ranking: %s")Production
Number of Features: 3
Selected Features: [ True False False False False True True False]
Feature Ranking: [1 2 3 5 6 1 1 4]Nous pouvons voir dans la sortie ci-dessus, RFE choisit preg, mass et pedi comme les 3 premières meilleures caractéristiques. Ils sont marqués par 1 dans la sortie.
Analyse en composantes principales (ACP)
La PCA, généralement appelée technique de réduction des données, est une technique de sélection de caractéristiques très utile car elle utilise l'algèbre linéaire pour transformer l'ensemble de données en une forme compressée. Nous pouvons implémenter la technique de sélection des fonctionnalités PCA à l'aide de la classe PCA de la bibliothèque Python scikit-learn. Nous pouvons sélectionner le nombre de composants principaux dans la sortie.
Exemple
Dans cet exemple, nous utiliserons PCA pour sélectionner les 3 meilleurs composants principaux de l'ensemble de données Pima Indians Diabetes.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesEnsuite, nous séparerons le tableau en composants d'entrée et de sortie -
X = array[:,0:8]
Y = array[:,8]Les lignes de code suivantes extrairont les fonctionnalités de l'ensemble de données -
pca = PCA(n_components=3)
fit = pca.fit(X)
print("Explained Variance: %s") % fit.explained_variance_ratio_
print(fit.components_)Production
Explained Variance: [ 0.88854663 0.06159078 0.02579012]
[[ -2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-02
9.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[ 2.26488861e-02 9.72210040e-01 1.41909330e-01 -5.78614699e-02
-9.46266913e-02 4.69729766e-02 8.16804621e-04 1.40168181e-01]
[ -2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-01
2.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]]Nous pouvons observer à partir de la sortie ci-dessus que 3 composants principaux ont peu de ressemblance avec les données source.
Importance des fonctionnalités
Comme son nom l'indique, la technique de l'importance des caractéristiques est utilisée pour choisir les caractéristiques d'importance. Il utilise essentiellement un classificateur supervisé formé pour sélectionner les fonctionnalités. Nous pouvons implémenter cette technique de sélection de fonctionnalités à l'aide de la classe ExtraTreeClassifier de la bibliothèque Python scikit-learn.
Exemple
Dans cet exemple, nous utiliserons ExtraTreeClassifier pour sélectionner des caractéristiques de l'ensemble de données Pima Indians Diabetes.
from pandas import read_csv
from sklearn.ensemble import ExtraTreesClassifier
path = r'C:\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(data, names=names)
array = dataframe.valuesEnsuite, nous séparerons le tableau en composants d'entrée et de sortie -
X = array[:,0:8]
Y = array[:,8]Les lignes de code suivantes extrairont les fonctionnalités de l'ensemble de données -
model = ExtraTreesClassifier()
model.fit(X, Y)
print(model.feature_importances_)Production
[ 0.11070069 0.2213717 0.08824115 0.08068703 0.07281761 0.14548537 0.12654214 0.15415431]À partir de la sortie, nous pouvons observer qu'il existe des scores pour chaque attribut. Plus le score est élevé, plus l'importance de cet attribut est élevée.
Introduction à la classification
La classification peut être définie comme le processus de prédiction d'une classe ou d'une catégorie à partir de valeurs observées ou de points de données donnés. La sortie catégorisée peut avoir la forme «noire» ou «blanche» ou «spam» ou «pas de spam».
Mathématiquement, la classification est la tâche d'approximer une fonction de mappage (f) des variables d'entrée (X) aux variables de sortie (Y). Il appartient essentiellement à l'apprentissage automatique supervisé dans lequel des cibles sont également fournies avec l'ensemble de données d'entrée.
Un exemple de problème de classification peut être la détection de spam dans les e-mails. Il ne peut y avoir que deux catégories de sortie, «spam» et «pas de spam»; il s'agit donc d'une classification de type binaire.
Pour implémenter cette classification, nous devons d'abord former le classificateur. Pour cet exemple, les e-mails «spam» et «pas de spam» seraient utilisés comme données d'entraînement. Après avoir entraîné avec succès le classificateur, il peut être utilisé pour détecter un e-mail inconnu.
Types d'apprenants en classification
Nous avons deux types d'apprenants en ce qui concerne les problèmes de classification -
Apprenants paresseux
Comme son nom l'indique, ce type d'apprenants attend que les données de test apparaissent après le stockage des données de formation. La classification est effectuée uniquement après avoir obtenu les données de test. Ils passent moins de temps à s'entraîner mais plus à prévoir. Des exemples d'apprenants paresseux sont le K-plus proche voisin et le raisonnement basé sur des cas.
Apprenants avides
Contrairement aux apprenants paresseux, les apprenants enthousiastes construisent un modèle de classification sans attendre que les données de test apparaissent après le stockage des données de formation. Ils passent plus de temps à s'entraîner mais moins à prévoir. Les arbres de décision, les bayes naïves et les réseaux de neurones artificiels (ANN) sont des exemples d'apprenants enthousiastes.
Construire un classificateur en Python
Scikit-learn, une bibliothèque Python pour l'apprentissage automatique peut être utilisée pour créer un classificateur en Python. Les étapes de construction d'un classificateur en Python sont les suivantes -
Étape 1: importation du package python nécessaire
Pour créer un classificateur à l'aide de scikit-learn, nous devons l'importer. Nous pouvons l'importer en utilisant le script suivant -
import sklearnÉtape 2: importation du jeu de données
Après avoir importé le package nécessaire, nous avons besoin d'un ensemble de données pour créer un modèle de prédiction de classification. Nous pouvons l'importer à partir du jeu de données sklearn ou en utiliser un autre selon nos besoins. Nous allons utiliser la base de données de diagnostic du cancer du sein du Wisconsin de sklearn. Nous pouvons l'importer à l'aide du script suivant -
from sklearn.datasets import load_breast_cancerLe script suivant chargera le jeu de données;
data = load_breast_cancer()Nous devons également organiser les données et cela peut être fait à l'aide des scripts suivants -
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']La commande suivante imprimera le nom des étiquettes, «malin» et «bénin» dans le cas de notre base de données.
print(label_names)La sortie de la commande ci-dessus est les noms des étiquettes -
['malignant' 'benign']Ces étiquettes sont mappées aux valeurs binaires 0 et 1. Malignant le cancer est représenté par 0 et Benign le cancer est représenté par 1.
Les noms et valeurs de caractéristiques de ces étiquettes peuvent être vus à l'aide des commandes suivantes -
print(feature_names[0])La sortie de la commande ci-dessus est les noms des fonctionnalités pour l'étiquette 0 ie Malignant cancer -
mean radiusDe même, les noms des caractéristiques pour l'étiquette peuvent être produits comme suit -
print(feature_names[1])La sortie de la commande ci-dessus est les noms des fonctionnalités pour l'étiquette 1 ie Benign cancer -
mean textureNous pouvons imprimer les caractéristiques de ces étiquettes à l'aide de la commande suivante -
print(features[0])Cela donnera la sortie suivante -
[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
4.601e-01 1.189e-01]Nous pouvons imprimer les caractéristiques de ces étiquettes à l'aide de la commande suivante -
print(features[1])Cela donnera la sortie suivante -
[2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
2.750e-01 8.902e-02]Étape 3: Organisation des données dans des ensembles de formation et de test
Comme nous devons tester notre modèle sur des données invisibles, nous allons diviser notre ensemble de données en deux parties: un ensemble d'apprentissage et un ensemble de test. Nous pouvons utiliser la fonction train_test_split () du package python sklearn pour diviser les données en ensembles. La commande suivante importera la fonction -
from sklearn.model_selection import train_test_splitMaintenant, la prochaine commande divisera les données en données d'entraînement et de test. Dans cet exemple, nous utilisons 40% des données à des fins de test et 60% des données à des fins de formation -
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)Étape 4 - Évaluation du modèle
Après avoir divisé les données en formation et en tests, nous devons construire le modèle. Nous utiliserons l'algorithme Naïve Bayes à cet effet. Les commandes suivantes importeront le module GaussianNB -
from sklearn.naive_bayes import GaussianNBMaintenant, initialisez le modèle comme suit -
gnb = GaussianNB()Ensuite, à l'aide de la commande suivante, nous pouvons entraîner le modèle -
model = gnb.fit(train, train_labels)Maintenant, à des fins d'évaluation, nous devons faire des prédictions. Cela peut être fait en utilisant la fonction prédire () comme suit -
preds = gnb.predict(test)
print(preds)Cela donnera la sortie suivante -
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0
1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0
1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0
1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0
1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0
0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1
0 0 1 1 0 1]Les séries ci-dessus de 0 et 1 en sortie sont les valeurs prédites pour le Malignant et Benign classes de tumeurs.
Étape 5 - Recherche de la précision
Nous pouvons trouver la précision du modèle construit à l'étape précédente en comparant les deux tableaux à savoir test_labels et preds. Nous utiliserons la fonction precision_score () pour déterminer la précision.
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965La sortie ci-dessus montre que le classificateur NaïveBayes est précis à 95,17%.
Mesures d'évaluation de la classification
Le travail n'est pas terminé même si vous avez terminé l'implémentation de votre application ou modèle Machine Learning. Il faut savoir dans quelle mesure notre modèle est efficace? Il peut y avoir différentes métriques d'évaluation, mais nous devons la choisir avec soin car le choix des métriques influe sur la manière dont les performances d'un algorithme d'apprentissage automatique sont mesurées et comparées.
Voici quelques-unes des mesures importantes d'évaluation de la classification parmi lesquelles vous pouvez choisir en fonction de votre ensemble de données et du type de problème:
Matrice de confusion
C'est le moyen le plus simple de mesurer les performances d'un problème de classification où la sortie peut être de deux ou plusieurs types de classes. Une matrice de confusion n'est rien d'autre qu'un tableau à deux dimensions, à savoir. "Réel" et "Prévu" et en outre, les deux dimensions ont "Vrais positifs (TP)", "Vrais négatifs (TN)", "Faux positifs (FP)", "Faux négatifs (FN)" comme indiqué ci-dessous -

True Positives (TP) - C'est le cas lorsque la classe réelle et la classe prévue du point de données sont égales à 1.
True Negatives (TN) - C'est le cas lorsque la classe réelle et la classe prévue du point de données sont égales à 0.
False Positives (FP) - C'est le cas lorsque la classe réelle du point de données est 0 et la classe prévue du point de données est 1.
False Negatives (FN) - C'est le cas lorsque la classe réelle du point de données est 1 et la classe prévue du point de données est 0.
Nous pouvons trouver la matrice de confusion à l'aide de la fonction confusion_matrix () de sklearn. Avec l'aide du script suivant, nous pouvons trouver la matrice de confusion du classificateur binaire construit ci-dessus -
from sklearn.metrics import confusion_matrixProduction
[[ 73 7]
[ 4 144]]Précision
Il peut être défini comme le nombre de prédictions correctes faites par notre modèle ML. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$$=\frac{+}{+++}$$Pour le classificateur binaire construit ci-dessus, TP + TN = 73 + 144 = 217 et TP + FP + FN + TN = 73 + 7 + 4 + 144 = 228.
Par conséquent, Précision = 217/228 = 0,951754385965 qui est identique à ce que nous avons calculé après la création de notre classificateur binaire.
Précision
La précision, utilisée dans les extractions de documents, peut être définie comme le nombre de documents corrects renvoyés par notre modèle ML. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$$=\frac{}{+FP}$$Pour le classificateur binaire construit ci-dessus, TP = 73 et TP + FP = 73 + 7 = 80.
Par conséquent, Précision = 73/80 = 0,915
Rappel ou sensibilité
Le rappel peut être défini comme le nombre de positifs renvoyés par notre modèle ML. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$$=\frac{}{+FN}$$Pour le classificateur binaire construit ci-dessus, TP = 73 et TP + FN = 73 + 4 = 77.
Par conséquent, précision = 73/77 = 0,94805
Spécificité
La spécificité, contrairement au rappel, peut être définie comme le nombre de négatifs renvoyés par notre modèle ML. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$$=\frac{N}{N+FP}$$Pour le classificateur binaire construit ci-dessus, TN = 144 et TN + FP = 144 + 7 = 151.
Par conséquent, Précision = 144/151 = 0,95364
Divers algorithmes de classification ML
Voici quelques algorithmes de classification ML importants -
Régression logistique
Machine à vecteurs de soutien (SVM)
Arbre de décision
Bayes naïves
Forêt aléatoire
Nous discuterons en détail de tous ces algorithmes de classification dans d'autres chapitres.
Applications
Certaines des applications les plus importantes des algorithmes de classification sont les suivantes:
Reconnaissance de la parole
Reconnaissance de l'écriture manuscrite
Identification biométrique
Classification des documents
Introduction à la régression logistique
La régression logistique est un algorithme de classification d'apprentissage supervisé utilisé pour prédire la probabilité d'une variable cible. La nature de la variable cible ou dépendante est dichotomique, ce qui signifie qu'il n'y aurait que deux classes possibles.
En termes simples, la variable dépendante est de nature binaire ayant des données codées soit 1 (signifie succès / oui) ou 0 (signifie échec / non).
Mathématiquement, un modèle de régression logistique prédit P (Y = 1) en fonction de X. C'est l'un des algorithmes ML les plus simples qui peut être utilisé pour divers problèmes de classification tels que la détection de spam, la prédiction du diabète, la détection du cancer, etc.
Types de régression logistique
Généralement, la régression logistique signifie la régression logistique binaire ayant des variables cibles binaires, mais il peut y avoir deux autres catégories de variables cibles qui peuvent être prédites par elle. Sur la base de ce nombre de catégories, la régression logistique peut être divisée en types suivants -
Binaire ou binomial
Dans un tel type de classification, une variable dépendante n'aura que deux types possibles, soit 1 et 0. Par exemple, ces variables peuvent représenter un succès ou un échec, oui ou non, une victoire ou une perte, etc.
Multinomial
Dans un tel type de classification, la variable dépendante peut avoir 3 types non ordonnés ou plus possibles ou les types n'ayant aucune signification quantitative. Par exemple, ces variables peuvent représenter «Type A» ou «Type B» ou «Type C».
Ordinal
Dans un tel type de classification, la variable dépendante peut avoir 3 types ordonnés ou plus possibles ou les types ayant une signification quantitative. Par exemple, ces variables peuvent représenter «mauvais» ou «bon», «très bon», «excellent» et chaque catégorie peut avoir des scores comme 0,1,2,3.
Hypothèses de régression logistique
Avant de plonger dans la mise en œuvre de la régression logistique, nous devons être conscients des hypothèses suivantes à propos du même -
En cas de régression logistique binaire, les variables cibles doivent toujours être binaires et le résultat souhaité est représenté par le facteur niveau 1.
Il ne doit pas y avoir de multi-colinéarité dans le modèle, ce qui signifie que les variables indépendantes doivent être indépendantes les unes des autres.
Nous devons inclure des variables significatives dans notre modèle.
Nous devrions choisir une grande taille d'échantillon pour la régression logistique.
Modèle de régression logistique binaire
La forme la plus simple de régression logistique est la régression logistique binaire ou binomiale dans laquelle la variable cible ou dépendante ne peut avoir que 2 types possibles, soit 1 ou 0. Elle nous permet de modéliser une relation entre plusieurs variables prédictives et une variable cible binaire / binomiale. En cas de régression logistique, la fonction linéaire est essentiellement utilisée comme entrée d'une autre fonction comme dans la relation suivante -
$h_{\theta}{(x)}=g(\theta^{T}x)ℎ 0≤h_{\theta}≤1$Voici la fonction logistique ou sigmoïde qui peut être donnée comme suit -
$g(z)= \frac{1}{1+e^{-z}}ℎ =\theta ^{T}$La courbe sigmoïde peut être représentée à l'aide du graphique suivant. Nous pouvons voir que les valeurs de l'axe y sont comprises entre 0 et 1 et croise l'axe à 0,5.

Les classes peuvent être divisées en positives ou négatives. La sortie relève de la probabilité de classe positive si elle est comprise entre 0 et 1. Pour notre implémentation, nous interprétons la sortie de la fonction d'hypothèse comme positive si elle est ≥0,5, sinon négative.
Nous devons également définir une fonction de perte pour mesurer les performances de l'algorithme en utilisant les poids sur les fonctions, représentés par thêta comme suit -
ℎ = ()
$J(\theta) = \frac{1}{m}.(-y^{T}log(h) - (1 -y)^Tlog(1-h))$Maintenant, après avoir défini la fonction de perte, notre objectif principal est de minimiser la fonction de perte. Cela peut être fait en ajustant les poids, c'est-à-dire en augmentant ou en diminuant les poids. Avec l'aide de dérivés de la fonction de perte pour chaque poids, nous pourrions savoir quels paramètres devraient avoir un poids élevé et lesquels devraient avoir un poids plus petit.
L'équation de descente de gradient suivante nous indique comment la perte changerait si nous modifiions les paramètres -
$\frac{()}{\theta_{j}}=\frac{1}{m}X^{T}(()−)$Implémentation en Python
Nous allons maintenant implémenter le concept ci-dessus de régression logistique binomiale en Python. À cette fin, nous utilisons un ensemble de données de fleurs multivariées nommé «iris» qui a 3 classes de 50 instances chacune, mais nous utiliserons les deux premières colonnes d'entités. Chaque classe représente un type de fleur d'iris.
Tout d'abord, nous devons importer les bibliothèques nécessaires comme suit -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasetsEnsuite, chargez le jeu de données iris comme suit -
iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1Nous pouvons tracer nos données d'entraînement s suit -
plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();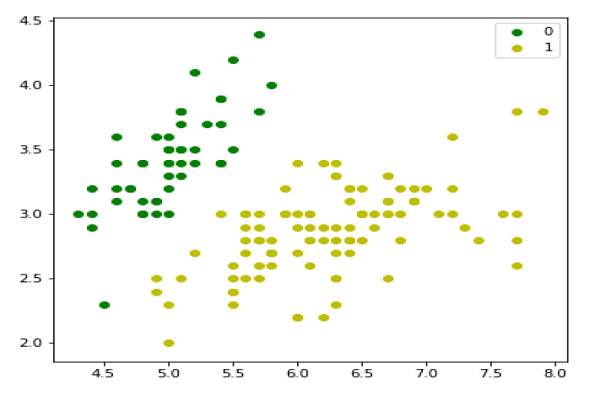
Ensuite, nous définirons la fonction sigmoïde, la fonction de perte et la descente du gradient comme suit -
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)Maintenant, initialisez les poids comme suit -
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
loss = self.__loss(h, y)
if(self.verbose ==True and i % 10000 == 0):
print(f'loss: {loss} \t')Avec l'aide du script suivant, nous pouvons prédire les probabilités de sortie -
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
return self.predict_prob(X).round()Ensuite, nous pouvons évaluer le modèle et le tracer comme suit -
model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()
plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
Modèle de régression logistique multinomiale
Une autre forme utile de régression logistique est la régression logistique multinomiale dans laquelle la variable cible ou dépendante peut avoir 3 types non ordonnés ou plus possibles, c'est-à-dire les types n'ayant aucune signification quantitative.
Implémentation en Python
Nous allons maintenant implémenter le concept ci-dessus de régression logistique multinomiale en Python. Pour cela, nous utilisons un ensemble de données de sklearn nommé digit.
Tout d'abord, nous devons importer les bibliothèques nécessaires comme suit -
Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_splitEnsuite, nous devons charger l'ensemble de données numériques -
digits = datasets.load_digits()Maintenant, définissez la matrice de caractéristiques (X) et le vecteur de réponse (y) comme suit -
X = digits.data
y = digits.targetAvec l'aide de la prochaine ligne de code, nous pouvons diviser X et y en ensembles d'entraînement et de test -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)Créez maintenant un objet de régression logistique comme suit -
digreg = linear_model.LogisticRegression()Maintenant, nous devons entraîner le modèle en utilisant les ensembles d'apprentissage comme suit -
digreg.fit(X_train, y_train)Ensuite, faites les prédictions sur l'ensemble de test comme suit -
y_pred = digreg.predict(X_test)Imprimez ensuite la précision du modèle comme suit -
print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)Production
Accuracy of Logistic Regression model is: 95.6884561891516À partir de la sortie ci-dessus, nous pouvons voir que la précision de notre modèle est d'environ 96%.
Introduction à SVM
Les machines vectorielles de support (SVM) sont des algorithmes d'apprentissage automatique supervisé puissants mais flexibles qui sont utilisés à la fois pour la classification et la régression. Mais généralement, ils sont utilisés dans les problèmes de classification. Dans les années 1960, les SVM ont été introduits pour la première fois, mais ils ont ensuite été affinés en 1990. Les SVM ont leur mode de mise en œuvre unique par rapport aux autres algorithmes d'apprentissage automatique. Dernièrement, ils sont extrêmement populaires en raison de leur capacité à gérer plusieurs variables continues et catégorielles.
Fonctionnement de SVM
Un modèle SVM est essentiellement une représentation de différentes classes dans un hyperplan dans un espace multidimensionnel. L'hyperplan sera généré de manière itérative par SVM afin que l'erreur puisse être minimisée. Le but de SVM est de diviser les ensembles de données en classes pour trouver un hyperplan marginal maximal (MMH).

Les éléments suivants sont des concepts importants dans SVM -
Support Vectors- Les points de données les plus proches de l'hyperplan sont appelés vecteurs de support. La ligne de séparation sera définie à l'aide de ces points de données.
Hyperplane - Comme on peut le voir sur le schéma ci-dessus, il s'agit d'un plan ou d'un espace de décision qui est divisé entre un ensemble d'objets de classes différentes.
Margin- Il peut être défini comme l'écart entre deux lignes sur les points de données placard de différentes classes. Elle peut être calculée comme la distance perpendiculaire de la ligne aux vecteurs de support. Une grande marge est considérée comme une bonne marge et une petite marge est considérée comme une mauvaise marge.
L'objectif principal de SVM est de diviser les ensembles de données en classes pour trouver un hyperplan marginal maximal (MMH) et cela peut être fait dans les deux étapes suivantes -
Premièrement, SVM générera des hyperplans de manière itérative qui séparent les classes de la meilleure façon.
Ensuite, il choisira l'hyperplan qui sépare correctement les classes.
Implémentation de SVM en Python
Pour implémenter SVM en Python, nous allons commencer par l'importation de bibliothèques standard comme suit -
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns; sns.set()Ensuite, nous créons un exemple de jeu de données, ayant des données linéairement séparables, à partir de sklearn.dataset.sample_generator pour la classification à l'aide de SVM -
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=0.50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');Ce qui suit serait la sortie après avoir généré un échantillon de données contenant 100 échantillons et 2 clusters -

Nous savons que SVM prend en charge la classification discriminante. il divise les classes les unes des autres en trouvant simplement une ligne en cas de deux dimensions ou une variété en cas de dimensions multiples. Il est implémenté sur l'ensemble de données ci-dessus comme suit -
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);La sortie est la suivante -

Nous pouvons voir à partir de la sortie ci-dessus qu'il existe trois séparateurs différents qui distinguent parfaitement les échantillons ci-dessus.
Comme discuté, l'objectif principal de SVM est de diviser les ensembles de données en classes pour trouver un hyperplan marginal maximal (MMH), donc plutôt que de tracer une ligne zéro entre les classes, nous pouvons dessiner autour de chaque ligne une marge d'une certaine largeur jusqu'au point le plus proche. Cela peut être fait comme suit -
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
À partir de l'image ci-dessus en sortie, nous pouvons facilement observer les «marges» dans les classificateurs discriminants. SVM choisira la ligne qui maximise la marge.
Ensuite, nous utiliserons le classificateur de vecteurs de support de Scikit-Learn pour entraîner un modèle SVM sur ces données. Ici, nous utilisons un noyau linéaire pour ajuster SVM comme suit -
from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1E10)
model.fit(X, y)La sortie est la suivante -
SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)Maintenant, pour une meilleure compréhension, ce qui suit va tracer les fonctions de décision pour SVC 2D -
def decision_function(model, ax=None, plot_support=True):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()Pour évaluer le modèle, nous devons créer une grille comme suit -
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)Ensuite, nous devons tracer les limites et les marges de décision comme suit -
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])Maintenant, tracez de la même manière les vecteurs de support comme suit -
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)Maintenant, utilisez cette fonction pour adapter nos modèles comme suit -
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
decision_function(model);
Nous pouvons observer à partir de la sortie ci-dessus qu'un classificateur SVM s'adapte aux données avec des marges, c'est-à-dire des lignes en pointillés et des vecteurs de support, les éléments pivots de cet ajustement, touchant la ligne en pointillé. Ces points de vecteur de support sont stockés dans l'attribut support_vectors_ du classificateur comme suit -
model.support_vectors_La sortie est la suivante -
array([[0.5323772 , 3.31338909],
[2.11114739, 3.57660449],
[1.46870582, 1.86947425]])Noyaux SVM
En pratique, l'algorithme SVM est implémenté avec un noyau qui transforme un espace de données d'entrée dans la forme requise. SVM utilise une technique appelée l'astuce du noyau dans laquelle le noyau prend un espace d'entrée de faible dimension et le transforme en un espace de dimension supérieure. En termes simples, le noyau convertit les problèmes non séparables en problèmes séparables en y ajoutant plus de dimensions. Cela rend SVM plus puissant, plus flexible et plus précis. Voici quelques-uns des types de noyaux utilisés par SVM -
Noyau linéaire
Il peut être utilisé comme produit scalaire entre deux observations quelconques. La formule du noyau linéaire est la suivante -
k (x, x i ) = somme (x * x i )
À partir de la formule ci-dessus, nous pouvons voir que le produit entre deux vecteurs dit & est la somme de la multiplication de chaque paire de valeurs d'entrée.
Noyau polynomial
Il s'agit d'une forme plus généralisée de noyau linéaire et distingue l'espace d'entrée courbe ou non linéaire. Voici la formule du noyau polynomial -
K (x, xi) = 1 + somme (x * xi) ^ d
Ici, d est le degré de polynôme, que nous devons spécifier manuellement dans l'algorithme d'apprentissage.
Noyau de fonction de base radiale (RBF)
Le noyau RBF, principalement utilisé dans la classification SVM, cartographie l'espace d'entrée dans un espace dimensionnel indéfini. La formule suivante l'explique mathématiquement -
K (x, xi) = exp (-gamma * somme ((x - xi ^ 2))
Ici, le gamma va de 0 à 1. Nous devons le spécifier manuellement dans l'algorithme d'apprentissage. Une bonne valeur par défaut de gamma est 0,1.
Comme nous avons implémenté SVM pour les données linéairement séparables, nous pouvons l'implémenter en Python pour les données qui ne sont pas linéairement séparables. Cela peut être fait en utilisant des noyaux.
Exemple
Voici un exemple de création d'un classificateur SVM à l'aide de noyaux. Nous utiliserons le jeu de données iris de scikit-learn -
Nous allons commencer par importer les packages suivants -
import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as pltMaintenant, nous devons charger les données d'entrée -
iris = datasets.load_iris()À partir de cet ensemble de données, nous prenons les deux premières caractéristiques comme suit -
X = iris.data[:, :2]
y = iris.targetEnsuite, nous allons tracer les limites SVM avec les données d'origine comme suit -
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]Maintenant, nous devons fournir la valeur du paramètre de régularisation comme suit -
C = 1.0Ensuite, l'objet classificateur SVM peut être créé comme suit -
Svc_classifier = svm.SVC (noyau = 'linéaire', C = C) .fit (X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')Production
Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')
Pour créer un classificateur SVM avec rbf noyau, nous pouvons changer le noyau en rbf comme suit -
Svc_classifier = svm.SVC(kernel='rbf', gamma =‘auto’,C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')Production
Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')
Nous mettons la valeur de gamma à «auto» mais vous pouvez également fournir sa valeur entre 0 et 1.
Avantages et inconvénients des classificateurs SVM
Avantages des classificateurs SVM
Les classificateurs SVM offrent une grande précision et fonctionnent bien avec un espace dimensionnel élevé. Les classificateurs SVM utilisent essentiellement un sous-ensemble de points d'entraînement, donc le résultat utilise très moins de mémoire.
Inconvénients des classificateurs SVM
Ils ont un temps de formation élevé et ne conviennent donc pas en pratique aux grands ensembles de données. Un autre inconvénient est que les classificateurs SVM ne fonctionnent pas bien avec des classes qui se chevauchent.
Introduction à l'arbre de décision
En général, l'analyse d'arbre de décision est un outil de modélisation prédictive qui peut être appliqué dans de nombreux domaines. Les arbres de décision peuvent être construits par une approche algorithmique qui peut diviser l'ensemble de données de différentes manières en fonction de différentes conditions. Les décisions tress sont les algorithmes les plus puissants qui entrent dans la catégorie des algorithmes supervisés.
Ils peuvent être utilisés à la fois pour des tâches de classification et de régression. Les deux principales entités d'un arbre sont les nœuds de décision, où les données sont divisées et partent, où nous avons obtenu le résultat. L'exemple d'un arbre binaire pour prédire si une personne est apte ou inapte, fournissant diverses informations comme l'âge, les habitudes alimentaires et les habitudes d'exercice, est donné ci-dessous -
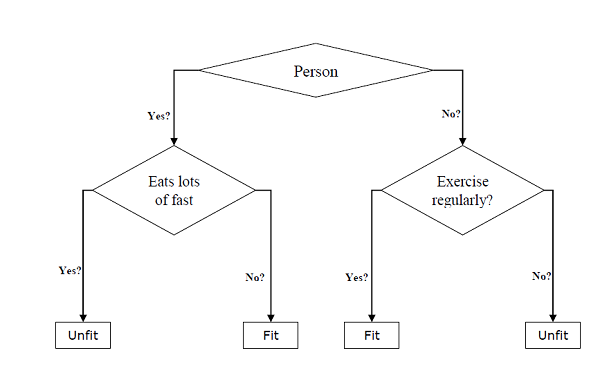
Dans l'arbre de décision ci-dessus, la question concerne les nœuds de décision et les résultats finaux sont les feuilles. Nous avons les deux types d'arbres de décision suivants -
Classification decision trees- Dans ce type d'arbres de décision, la variable de décision est catégorique. L'arbre de décision ci-dessus est un exemple d'arbre de décision de classification.
Regression decision trees - Dans ce type d'arbres de décision, la variable de décision est continue.
Implémentation de l'algorithme d'arbre de décision
Index de Gini
C'est le nom de la fonction de coût qui est utilisée pour évaluer les fractionnements binaires dans le jeu de données et qui fonctionne avec la variable cible catégorielle «Succès» ou «Échec».
Plus la valeur de l'indice de Gini est élevée, plus l'homogénéité est élevée. Une valeur d'indice de Gini parfaite est 0 et la pire est 0,5 (pour le problème à 2 classes). L'indice de Gini pour un fractionnement peut être calculé à l'aide des étapes suivantes -
Tout d'abord, calculez l'indice de Gini pour les sous-nœuds en utilisant la formule p ^ 2 + q ^ 2, qui est la somme du carré de probabilité de succès et d'échec.
Ensuite, calculez l'indice de Gini pour la division en utilisant le score de Gini pondéré de chaque nœud de cette division.
L'algorithme CART (Classification and Regression Tree) utilise la méthode Gini pour générer des fractionnements binaires.
Création fractionnée
Un fractionnement comprend essentiellement un attribut dans l'ensemble de données et une valeur. Nous pouvons créer une division dans l'ensemble de données à l'aide des trois parties suivantes -
Part1 - Calcul du score de Gini: Nous venons de discuter de cette partie dans la section précédente.
Part2- Fractionnement d'un ensemble de données: il peut être défini comme séparant un ensemble de données en deux listes de lignes ayant l'index d'un attribut et une valeur de fractionnement de cet attribut. Après avoir récupéré les deux groupes - droite et gauche, à partir du jeu de données, nous pouvons calculer la valeur de la division en utilisant le score de Gini calculé en première partie. La valeur de fractionnement décidera dans quel groupe l'attribut résidera.
Part3- Évaluation de toutes les divisions: La partie suivante après avoir trouvé le score de Gini et le jeu de données de division est l'évaluation de toutes les divisions. Pour cela, nous devons d'abord vérifier chaque valeur associée à chaque attribut en tant que fractionnement candidat. Ensuite, nous devons trouver la meilleure répartition possible en évaluant le coût de la répartition. La meilleure division sera utilisée comme nœud dans l'arbre de décision.
Construire un arbre
Comme nous le savons, un arbre a un nœud racine et des nœuds terminaux. Après avoir créé le nœud racine, nous pouvons construire l'arbre en suivant deux parties -
Partie 1: création du nœud terminal
Lors de la création de nœuds terminaux de l'arbre de décision, un point important est de décider quand arrêter la croissance de l'arbre ou créer d'autres nœuds terminaux. Cela peut être fait en utilisant deux critères à savoir la profondeur maximale de l'arbre et les enregistrements de nœuds minimum comme suit -
Maximum Tree Depth- Comme son nom l'indique, il s'agit du nombre maximum de nœuds dans une arborescence après le nœud racine. Il faut arrêter d'ajouter des nœuds terminaux une fois qu'un arbre atteint à la profondeur maximale c'est à dire une fois qu'un arbre a obtenu le nombre maximum de nœuds terminaux.
Minimum Node Records- Il peut être défini comme le nombre minimum de modèles d'apprentissage dont un nœud donné est responsable. Nous devons arrêter d'ajouter des nœuds terminaux une fois que l'arbre atteint ces enregistrements de nœuds minimum ou en dessous de ce minimum.
Le nœud terminal est utilisé pour faire une prédiction finale.
Partie 2: Fractionnement récursif
Comme nous avons compris quand créer des nœuds terminaux, nous pouvons maintenant commencer à construire notre arbre. Le fractionnement récursif est une méthode pour construire l'arbre. Dans cette méthode, une fois qu'un nœud est créé, nous pouvons créer les nœuds enfants (nœuds ajoutés à un nœud existant) de manière récursive sur chaque groupe de données, générés en fractionnant l'ensemble de données, en appelant encore et encore la même fonction.
Prédiction
Après avoir construit un arbre de décision, nous devons faire une prédiction à ce sujet. Fondamentalement, la prédiction consiste à naviguer dans l'arbre de décision avec la ligne de données spécifiquement fournie.
Nous pouvons faire une prédiction à l'aide de la fonction récursive, comme ci-dessus. La même routine de prédiction est appelée à nouveau avec les nœuds gauche ou droit enfant.
Hypothèses
Voici quelques-unes des hypothèses que nous faisons lors de la création de l'arbre de décision -
Lors de la préparation des arbres de décision, l'ensemble d'apprentissage est en tant que nœud racine.
Le classificateur d'arbre de décision préfère que les valeurs des caractéristiques soient catégoriques. Dans le cas où vous souhaitez utiliser des valeurs continues, elles doivent être discrétisées avant la création du modèle.
En fonction des valeurs de l'attribut, les enregistrements sont distribués de manière récursive.
Une approche statistique sera utilisée pour placer des attributs à n'importe quelle position de nœud, à savoir le nœud racine ou le nœud interne.
Implémentation en Python
Exemple
Dans l'exemple suivant, nous allons implémenter le classificateur Arbre de décision sur le diabète indien Pima -
Tout d'abord, commencez par importer les packages Python nécessaires -
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_splitEnsuite, téléchargez le jeu de données iris à partir de son lien Web comme suit -
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()pregnant glucose bp skin insulin bmi pedigree age label
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1Maintenant, divisez l'ensemble de données en entités et variable cible comme suit -
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableEnsuite, nous diviserons les données en train et test split. Le code suivant divisera l'ensemble de données en 70% de données d'entraînement et 30% de données de test -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)Ensuite, entraînez le modèle à l'aide de la classe DecisionTreeClassifier de sklearn comme suit -
clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)Enfin, nous devons faire des prédictions. Cela peut être fait à l'aide du script suivant -
y_pred = clf.predict(X_test)Ensuite, nous pouvons obtenir le score de précision, la matrice de confusion et le rapport de classification comme suit -
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Production
Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
precision recall f1-score support
0 0.72 0.79 0.75 146
1 0.57 0.46 0.51 85
micro avg 0.67 0.67 0.67 231
macro avg 0.64 0.63 0.63 231
weighted avg 0.66 0.67 0.66 231
Accuracy: 0.670995670995671Visualiser l'arbre de décision
L'arbre de décision ci-dessus peut être visualisé à l'aide du code suivant -
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())
Introduction à l'algorithme naïf de Bayes
Les algorithmes naïfs de Bayes sont une technique de classification basée sur l'application du théorème de Bayes avec une forte hypothèse que tous les prédicteurs sont indépendants les uns des autres. En termes simples, l'hypothèse est que la présence d'une caractéristique dans une classe est indépendante de la présence de toute autre caractéristique de la même classe. Par exemple, un téléphone peut être considéré comme intelligent s'il possède un écran tactile, une connexion Internet, un bon appareil photo, etc. Bien que toutes ces fonctionnalités dépendent les unes des autres, elles contribuent indépendamment à la probabilité que le téléphone soit un téléphone intelligent.
Dans la classification bayésienne, l'intérêt principal est de trouver les probabilités postérieures c'est-à-dire la probabilité d'une étiquette compte tenu de certaines caractéristiques observées, (|). Avec l'aide du théorème de Bayes, nous pouvons l'exprimer sous forme quantitative comme suit -
$P(L |features)= \frac{P(L)P(features |L)}{()}$Ici, (|) est la probabilité postérieure de classe.
() est la probabilité a priori de classe.
(|) est la vraisemblance qui est la probabilité du prédicteur de la classe donnée.
() est la probabilité a priori du prédicteur.
Modèle de construction utilisant Naïve Bayes en Python
Bibliothèque Python, Scikit learn est la bibliothèque la plus utile qui nous aide à construire un modèle Naïve Bayes en Python. Nous avons les trois types suivants de modèle Naïve Bayes sous Scikit learn Python library -
Bayes naïves gaussiennes
Il s'agit du classificateur Naïve Bayes le plus simple en supposant que les données de chaque étiquette sont tirées d'une simple distribution gaussienne.
Bayes naïves multinomiales
Un autre classificateur Naïve Bayes utile est le Multinomial Naïve Bayes dans lequel les caractéristiques sont supposées être tirées d'une simple distribution multinomiale. Ce type de bayes naïves est le plus approprié pour les caractéristiques qui représentent des comptages discrets.
Bernoulli Naïve Bayes
Un autre modèle important est Bernoulli Naïve Bayes dans lequel les caractéristiques sont supposées être binaires (0 et 1). La classification de texte avec le modèle «sac de mots» peut être une application de Bernoulli Naïve Bayes.
Exemple
En fonction de notre ensemble de données, nous pouvons choisir l'un des modèles Naïve Bayes expliqué ci-dessus. Ici, nous implémentons le modèle Gaussian Naïve Bayes en Python -
Nous commencerons par les importations requises comme suit -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()Maintenant, en utilisant la fonction make_blobs () de Scikit learn, nous pouvons générer des blobs de points avec une distribution gaussienne comme suit -
from sklearn.datasets import make_blobs
X, y = make_blobs(300, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');Ensuite, pour utiliser le modèle GaussianNB, nous devons importer et créer son objet comme suit -
from sklearn.naive_bayes import GaussianNB
model_GBN = GaussianNB()
model_GNB.fit(X, y);Maintenant, nous devons faire des prédictions. Cela peut être fait après avoir généré de nouvelles données comme suit -
rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model_GNB.predict(Xnew)Ensuite, nous traçons de nouvelles données pour trouver ses limites -
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='summer', alpha=0.1)
plt.axis(lim);Maintenant, à l'aide de la ligne de codes suivante, nous pouvons trouver les probabilités postérieures des première et deuxième étiquettes -
yprob = model_GNB.predict_proba(Xnew)
yprob[-10:].round(3)Production
array([[0.998, 0.002],
[1. , 0. ],
[0.987, 0.013],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[0. , 1. ],
[0.986, 0.014]])Avantages et inconvénients
Avantages
Voici quelques avantages de l'utilisation des classificateurs Naïve Bayes -
La classification Naïve Bayes est facile à mettre en œuvre et rapide.
Elle convergera plus vite que les modèles discriminants comme la régression logistique.
Cela nécessite moins de données d'entraînement.
Il est de nature hautement évolutive ou évolue de manière linéaire avec le nombre de prédicteurs et de points de données.
Il peut faire des prédictions probabilistes et traiter des données continues et discrètes.
L'algorithme de classification naïve de Bayes peut être utilisé pour les problèmes de classification binaires et multi-classes.
Les inconvénients
Voici quelques inconvénients de l'utilisation des classificateurs Naïve Bayes -
L'un des inconvénients les plus importants de la classification Naïve Bayes est sa forte indépendance des fonctionnalités, car dans la vie réelle, il est presque impossible d'avoir un ensemble de fonctionnalités complètement indépendantes les unes des autres.
Un autre problème avec la classification Naïve Bayes est sa `` fréquence zéro '' qui signifie que si une variable catégorielle a une catégorie mais n'est pas observée dans l'ensemble de données d'apprentissage, alors le modèle Naïve Bayes lui attribuera une probabilité nulle et il sera incapable de faire un prédiction.
Applications de la classification Naïve Bayes
Voici quelques applications courantes de la classification Naïve Bayes -
Real-time prediction - En raison de sa facilité de mise en œuvre et de son calcul rapide, il peut être utilisé pour faire des prédictions en temps réel.
Multi-class prediction - L'algorithme de classification Naïve Bayes peut être utilisé pour prédire la probabilité postérieure de plusieurs classes de variable cible.
Text classification- En raison de la fonctionnalité de prédiction multi-classes, les algorithmes de classification Naïve Bayes sont bien adaptés à la classification de texte. C'est pourquoi il est également utilisé pour résoudre des problèmes tels que le filtrage du spam et l'analyse des sentiments.
Recommendation system - En plus des algorithmes tels que le filtrage collaboratif, Naïve Bayes crée un système de recommandation qui peut être utilisé pour filtrer les informations invisibles et pour prédire la météo qu'un utilisateur souhaite ou non à la ressource donnée.
introduction
Random forest est un algorithme d'apprentissage supervisé qui est utilisé à la fois pour la classification et la régression. Mais cependant, il est principalement utilisé pour les problèmes de classification. Comme nous le savons, une forêt est composée d'arbres et plus d'arbres signifie une forêt plus robuste. De même, l'algorithme de forêt aléatoire crée des arbres de décision sur des échantillons de données, puis obtient la prédiction de chacun d'eux et sélectionne finalement la meilleure solution par vote. C'est une méthode d'ensemble qui est meilleure qu'un arbre de décision unique car elle réduit le surajustement en faisant la moyenne du résultat.
Fonctionnement de l'algorithme de forêt aléatoire
Nous pouvons comprendre le fonctionnement de l'algorithme Random Forest à l'aide des étapes suivantes -
Step1 - Commencez par sélectionner des échantillons aléatoires à partir d'un ensemble de données donné.
Step2- Ensuite, cet algorithme construira un arbre de décision pour chaque échantillon. Ensuite, il obtiendra le résultat de la prédiction de chaque arbre de décision.
Step3 - Dans cette étape, le vote sera effectué pour chaque résultat prévu.
Step4 - Enfin, sélectionnez le résultat de prédiction le plus voté comme résultat de prédiction final.
Le schéma suivant illustrera son fonctionnement -

Implémentation en Python
Tout d'abord, commencez par importer les packages Python nécessaires -
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdEnsuite, téléchargez le jeu de données iris à partir de son lien Web comme suit -
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Ensuite, nous devons attribuer des noms de colonne à l'ensemble de données comme suit -
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Maintenant, nous devons lire l'ensemble de données dans le cadre de données pandas comme suit -
dataset = pd.read_csv(path, names=headernames)
dataset.head()longueur sépale |
largeur sépale |
pétale |
largeur des pétales |
Classe |
|
|---|---|---|---|---|---|
0 |
5.1 |
3,5 |
1,4 |
0,2 |
Iris-setosa |
1 |
4,9 |
3.0 |
1,4 |
0,2 |
Iris-setosa |
2 |
4.7 |
3.2 |
1.3 |
0,2 |
Iris-setosa |
3 |
4.6 |
3.1 |
1,5 |
0,2 |
Iris-setosa |
4 |
5,0 |
3,6 |
1,4 |
0,2 |
Iris-setosa |
Le prétraitement des données sera effectué à l'aide des lignes de script suivantes -
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].valuesEnsuite, nous diviserons les données en train et test split. Le code suivant divisera l'ensemble de données en 70% de données d'entraînement et 30% de données de test -
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)Ensuite, entraînez le modèle à l'aide de la classe RandomForestClassifier de sklearn comme suit -
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators=50)
classifier.fit(X_train, y_train)Enfin, nous devons faire des prédictions. Cela peut être fait à l'aide du script suivant -
y_pred = classifier.predict(X_test)Ensuite, imprimez les résultats comme suit -
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Production
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777Avantages et inconvénients de Random Forest
Avantages
Voici les avantages de l'algorithme Random Forest -
Il surmonte le problème du surajustement en faisant la moyenne ou en combinant les résultats de différents arbres de décision.
Les forêts aléatoires fonctionnent bien pour une large gamme d'éléments de données qu'un seul arbre de décision.
La forêt aléatoire a moins de variance qu'un arbre de décision unique.
Les forêts aléatoires sont très flexibles et possèdent une très grande précision.
La mise à l'échelle des données ne nécessite pas d'algorithme de forêt aléatoire. Il maintient une bonne précision même après avoir fourni des données sans mise à l'échelle.
La mise à l'échelle des données ne nécessite pas d'algorithme de forêt aléatoire. Il maintient une bonne précision même après avoir fourni des données sans mise à l'échelle.
Les inconvénients
Voici les inconvénients de l'algorithme Random Forest -
La complexité est le principal inconvénient des algorithmes de forêt aléatoire.
La construction de forêts aléatoires est beaucoup plus difficile et prend du temps que les arbres de décision.
Plus de ressources de calcul sont nécessaires pour implémenter l'algorithme Random Forest.
C'est moins intuitif dans le cas où nous avons une grande collection d'arbres de décision.
Le processus de prédiction utilisant des forêts aléatoires prend beaucoup de temps par rapport à d'autres algorithmes.
Introduction à la régression
La régression est un autre outil statistique et d'apprentissage automatique important et largement utilisé. L'objectif principal des tâches basées sur la régression est de prédire les étiquettes de sortie ou les réponses qui sont des valeurs numériques continues, pour les données d'entrée données. Le résultat sera basé sur ce que le modèle a appris lors de la phase de formation. Fondamentalement, les modèles de régression utilisent les caractéristiques des données d'entrée (variables indépendantes) et leurs valeurs de sortie numériques continues correspondantes (variables dépendantes ou de résultat) pour apprendre une association spécifique entre les entrées et les sorties correspondantes.

Types de modèles de régression

Les modèles de régression sont des deux types suivants:
Simple regression model - Il s'agit du modèle de régression le plus élémentaire dans lequel les prédictions sont formées à partir d'une seule caractéristique univariée des données.
Multiple regression model - Comme son nom l'indique, dans ce modèle de régression, les prédictions sont formées à partir de multiples caractéristiques des données.
Construire un régresseur en Python
Le modèle de régresseur en Python peut être construit comme nous avons construit le classificateur. Scikit-learn, une bibliothèque Python pour l'apprentissage automatique peut également être utilisée pour créer un régresseur en Python.
Dans l'exemple suivant, nous allons construire un modèle de régression de base qui ajustera une ligne aux données, c'est-à-dire un régresseur linéaire. Les étapes nécessaires pour créer un régresseur en Python sont les suivantes:
Étape 1: importation du package python nécessaire
Pour construire un régresseur à l'aide de scikit-learn, nous devons l'importer avec les autres packages nécessaires. Nous pouvons importer le en utilisant le script suivant -
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as pltÉtape 2: importation du jeu de données
Après avoir importé le package nécessaire, nous avons besoin d'un ensemble de données pour créer un modèle de prédiction de régression. Nous pouvons l'importer à partir du jeu de données sklearn ou en utiliser un autre selon nos besoins. Nous allons utiliser nos données d'entrée enregistrées. Nous pouvons l'importer à l'aide du script suivant -
input = r'C:\linear.txt'Ensuite, nous devons charger ces données. Nous utilisons la fonction np.loadtxt pour le charger.
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]Étape 3: Organisation des données dans des ensembles de formation et de test
Comme nous devons tester notre modèle sur des données invisibles, nous diviserons notre ensemble de données en deux parties: un ensemble d'apprentissage et un ensemble de test. La commande suivante l'exécutera -
training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]Étape 4 - Évaluation et prédiction du modèle
Après avoir divisé les données en formation et en tests, nous devons construire le modèle. Nous utiliserons pour cela la fonction LineaRegression () de Scikit-learn. La commande suivante créera un objet régresseur linéaire.
reg_linear= linear_model.LinearRegression()Ensuite, entraînez ce modèle avec les exemples d'apprentissage comme suit -
reg_linear.fit(X_train, y_train)Maintenant, nous devons enfin faire la prédiction avec les données de test.
y_test_pred = reg_linear.predict(X_test)Étape 5 - Tracé et visualisation
Après la prédiction, nous pouvons le tracer et le visualiser à l'aide du script suivant -
plt.scatter(X_test, y_test, color='red')
plt.plot(X_test, y_test_pred, color='black', linewidth=2)
plt.xticks(())
plt.yticks(())
plt.show()Production

Dans la sortie ci-dessus, nous pouvons voir la ligne de régression entre les points de données.
Step6- Performance computation - Nous pouvons également calculer les performances de notre modèle de régression à l'aide de diverses métriques de performances comme suit -
print("Regressor model performance:")
print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))Production
Regressor model performance:
Mean absolute error(MAE) = 1.78
Mean squared error(MSE) = 3.89
Median absolute error = 2.01
Explain variance score = -0.09
R2 score = -0.09Types d'algorithmes de régression ML
L'algorithme de régression ML le plus utile et le plus populaire est l'algorithme de régression linéaire qui se divise en deux types, à savoir -
Algorithme de régression linéaire simple
Algorithme de régression linéaire multiple.
Nous en discuterons et l'implémenterons en Python dans le chapitre suivant.
Applications
Les applications des algorithmes de régression ML sont les suivantes -
Forecasting or Predictive analysis- L'une des utilisations importantes de la régression est la prévision ou l'analyse prédictive. Par exemple, nous pouvons prévoir le PIB, les prix du pétrole ou en termes simples les données quantitatives qui changent avec le temps.
Optimization- Nous pouvons optimiser les processus métier à l'aide de la régression. Par exemple, un gérant de magasin peut créer un modèle statistique pour comprendre l'heure de la venue des clients.
Error correction- En affaires, prendre la bonne décision est tout aussi important que l'optimisation du processus métier. La régression peut également nous aider à prendre une décision correcte en corrigeant la décision déjà mise en œuvre.
Economics- C'est l'outil le plus utilisé en économie. Nous pouvons utiliser la régression pour prédire l'offre, la demande, la consommation, l'investissement dans les stocks, etc.
Finance- Une société financière est toujours intéressée par la minimisation du portefeuille de risques et souhaite connaître les facteurs qui affectent les clients. Tout cela peut être prédit à l'aide d'un modèle de régression.
Introduction à la régression linéaire
La régression linéaire peut être définie comme le modèle statistique qui analyse la relation linéaire entre une variable dépendante avec un ensemble donné de variables indépendantes. La relation linéaire entre les variables signifie que lorsque la valeur d'une ou de plusieurs variables indépendantes change (augmente ou diminue), la valeur de la variable dépendante change également en conséquence (augmente ou diminue).
Mathématiquement, la relation peut être représentée à l'aide de l'équation suivante -
Y = mX + b
Ici, Y est la variable dépendante que nous essayons de prédire
X est la variable dépendante que nous utilisons pour faire des prédictions.
m est la pente de la droite de régression qui représente l'effet de X sur Y
b est une constante, connue sous le nom d'ordonnée à l'origine. Si X = 0, Y serait égal à b.
De plus, la relation linéaire peut être de nature positive ou négative comme expliqué ci-dessous -
Relation linéaire positive
Une relation linéaire sera dite positive si la variable indépendante et dépendante augmente. Il peut être compris à l'aide du graphique suivant -

Relation linéaire négative
Une relation linéaire sera dite positive si indépendante augmente et si la variable dépendante diminue. Il peut être compris à l'aide du graphique suivant -

Types de régression linéaire
La régression linéaire est des deux types suivants -
Régression linéaire simple
Régression linéaire multiple
Régression linéaire simple (SLR)
C'est la version la plus basique de la régression linéaire qui prédit une réponse en utilisant une seule caractéristique. L'hypothèse dans SLR est que les deux variables sont linéairement liées.
Implémentation Python
Nous pouvons implémenter SLR en Python de deux manières, l'une consiste à fournir votre propre ensemble de données et l'autre à utiliser l'ensemble de données de la bibliothèque python scikit-learn.
Example1 - Dans l'exemple d'implémentation Python suivant, nous utilisons notre propre ensemble de données.
Tout d'abord, nous allons commencer par importer les packages nécessaires comme suit -
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltEnsuite, définissez une fonction qui calculera les valeurs importantes pour SLR -
def coef_estimation(x, y):La ligne de script suivante donnera le nombre d'observations n -
n = np.size(x)La moyenne des vecteurs x et y peut être calculée comme suit -
m_x, m_y = np.mean(x), np.mean(y)Nous pouvons trouver la déviation croisée et la déviation autour de x comme suit -
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xEnsuite, les coefficients de régression, c'est-à-dire b, peuvent être calculés comme suit -
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Ensuite, nous devons définir une fonction qui tracera la droite de régression et qui prédira le vecteur de réponse -
def plot_regression_line(x, y, b):La ligne de script suivante trace les points réels sous forme de nuage de points -
plt.scatter(x, y, color = "m", marker = "o", s = 30)La ligne de script suivante prédira le vecteur de réponse -
y_pred = b[0] + b[1]*xLes lignes de script suivantes traceront la ligne de régression et mettront les étiquettes dessus -
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Enfin, nous devons définir la fonction main () pour fournir un ensemble de données et appeler la fonction que nous avons définie ci-dessus -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Production
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788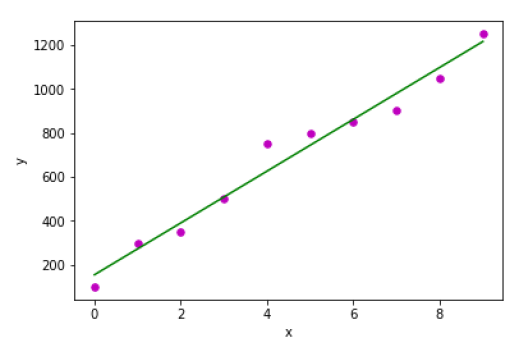
Example2 - Dans l'exemple d'implémentation Python suivant, nous utilisons l'ensemble de données sur le diabète de scikit-learn.
Tout d'abord, nous allons commencer par importer les packages nécessaires comme suit -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreEnsuite, nous allons charger le jeu de données sur le diabète et créer son objet -
diabetes = datasets.load_diabetes()Comme nous implémentons SLR, nous n'utiliserons qu'une seule fonctionnalité comme suit -
X = diabetes.data[:, np.newaxis, 2]Ensuite, nous devons diviser les données en ensembles d'entraînement et de test comme suit -
X_train = X[:-30]
X_test = X[-30:]Ensuite, nous devons diviser la cible en ensembles de formation et de test comme suit -
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Maintenant, pour entraîner le modèle, nous devons créer un objet de régression linéaire comme suit -
regr = linear_model.LinearRegression()Ensuite, entraînez le modèle à l'aide des ensembles d'apprentissage comme suit:
regr.fit(X_train, y_train)Ensuite, faites des prédictions en utilisant l'ensemble de test comme suit -
y_pred = regr.predict(X_test)Ensuite, nous imprimerons un coefficient comme MSE, le score de variance, etc. comme suit -
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Maintenant, tracez les sorties comme suit -
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Production
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Régression linéaire multiple (MLR)
C'est l'extension de la régression linéaire simple qui prédit une réponse en utilisant deux ou plusieurs caractéristiques. Mathématiquement, nous pouvons l'expliquer comme suit -
Considérons un ensemble de données ayant n observations, p caractéristiques, c'est-à-dire des variables indépendantes et y comme une réponse, c'est-à-dire une variable dépendante, la droite de régression pour p caractéristiques peut être calculée comme suit
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}$Ici, h (x i ) est la valeur de réponse prédite et b 0 , b 1 , b 2 â € ¦, b p sont les coefficients de régression.
Les modèles de régression linéaire multiple incluent toujours les erreurs dans les données appelées erreur résiduelle qui modifie le calcul comme suit -
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}+e_{i}$Nous pouvons également écrire l'équation ci-dessus comme suit -
$y_{i}=h(x_{i})+e_{i}$ $e_{i}= y_{i} - h(x_{i})$Implémentation Python
dans cet exemple, nous utiliserons l'ensemble de données sur le logement de Boston de scikit learn -
Tout d'abord, nous allons commencer par importer les packages nécessaires comme suit -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsEnsuite, chargez l'ensemble de données comme suit -
boston = datasets.load_boston(return_X_y=False)Les lignes de script suivantes définiront la matrice de caractéristiques, X et le vecteur de réponse, Y -
X = boston.data
y = boston.targetEnsuite, divisez l'ensemble de données en ensembles d'entraînement et de test comme suit:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)Maintenant, créez un objet de régression linéaire et entraînez le modèle comme suit -
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Production
Coefficients:
[-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01]
Variance score: 0.709454060230326
Hypothèses
Voici quelques hypothèses sur le jeu de données réalisé par le modèle de régression linéaire -
Multi-collinearity- Le modèle de régression linéaire suppose qu'il y a très peu ou pas de multi-colinéarité dans les données. Fondamentalement, la multi-colinéarité se produit lorsque les variables ou entités indépendantes ont une dépendance en elles.
Auto-correlation- Une autre hypothèse que le modèle de régression linéaire suppose qu'il y a très peu ou pas d'autocorrélation dans les données. Fondamentalement, l'autocorrélation se produit lorsqu'il existe une dépendance entre les erreurs résiduelles.
Relationship between variables - Le modèle de régression linéaire suppose que la relation entre les variables de réponse et de caractéristique doit être linéaire.
Introduction au clustering
Les méthodes de clustering sont l'une des méthodes de ML non supervisées les plus utiles. Ces méthodes sont utilisées pour trouver la similitude ainsi que les modèles de relation entre les échantillons de données, puis regrouper ces échantillons en groupes ayant une similitude basée sur des caractéristiques.
Le regroupement est important car il détermine le regroupement intrinsèque parmi les données non étiquetées actuelles. Ils font essentiellement des hypothèses sur les points de données pour constituer leur similitude. Chaque hypothèse construira des clusters différents mais tout aussi valides.
Par exemple, ci-dessous est le diagramme qui montre le système de clustering regroupé le même type de données dans différents clusters -

Méthodes de formation de cluster
Il n'est pas nécessaire que les grappes soient formées sous forme sphérique. Voici quelques autres méthodes de formation de cluster -
Basé sur la densité
Dans ces méthodes, les grappes sont formées comme la région dense. L'avantage de ces méthodes est qu'elles ont une bonne précision ainsi qu'une bonne capacité à fusionner deux clusters. Ex. Clustering spatial basé sur la densité d'applications avec bruit (DBSCAN), points de commande pour identifier la structure de clustering (OPTICS), etc.
Basé sur la hiérarchie
Dans ces méthodes, les clusters sont formés comme une structure de type arborescente basée sur la hiérarchie. Ils ont deux catégories à savoir, agglomérative (approche ascendante) et divisive (approche descendante). Ex. Clustering à l'aide de représentants (CURE), Clustering itératif équilibré de réduction à l'aide de hiérarchies (BIRCH), etc.
Partitionnement
Dans ces méthodes, les clusters sont formés en divisant les objets en k clusters. Le nombre de clusters sera égal au nombre de partitions. Ex. K-means, regroupement de grandes applications basées sur une recherche aléatoire (CLARANS).
la grille
Dans ces méthodes, les clusters sont formés comme une structure en forme de grille. L'avantage de ces méthodes est que toutes les opérations de clustering effectuées sur ces grilles sont rapides et indépendantes du nombre d'objets de données. Ex. Grille d'information statistique (STING), Clustering in Quest (CLIQUE).
Mesurer les performances du clustering
L'une des considérations les plus importantes concernant le modèle ML est d'évaluer ses performances ou vous pouvez dire la qualité du modèle. Dans le cas d'algorithmes d'apprentissage supervisé, évaluer la qualité de notre modèle est facile car nous avons déjà des étiquettes pour chaque exemple.
D'un autre côté, dans le cas d'algorithmes d'apprentissage non supervisés, nous ne sommes pas très chanceux car nous traitons des données non étiquetées. Mais nous avons encore quelques métriques qui donnent au praticien un aperçu de la survenance du changement dans les clusters en fonction de l'algorithme.
Avant de plonger en profondeur dans de telles métriques, nous devons comprendre que ces métriques évaluent uniquement les performances comparatives des modèles les uns par rapport aux autres plutôt que de mesurer la validité de la prédiction du modèle. Voici quelques-unes des métriques que nous pouvons déployer sur des algorithmes de clustering pour mesurer la qualité du modèle -
Analyse de la silhouette
Analyse de silhouette utilisée pour vérifier la qualité du modèle de clustering en mesurant la distance entre les clusters. Il nous fournit essentiellement un moyen d'évaluer les paramètres tels que le nombre de clusters à l'aide deSilhouette score. Ce score mesure à quel point chaque point d'un cluster est proche des points des clusters voisins.
Analyse du score de silhouette
La plage de score de Silhouette est [-1, 1]. Son analyse est la suivante -
+1 Score - Près de +1 Silhouette score indique que l'échantillon est éloigné de son cluster voisin.
0 Score - 0 Silhouette score indique que l'échantillon est sur ou très proche de la frontière de décision séparant deux clusters voisins.
-1 Score & moins -1 Silhouette score indique que les échantillons ont été affectés aux mauvais clusters.
Le calcul du score Silhouette peut être effectué en utilisant la formule suivante -
= (-) / (,)
Ici, = distance moyenne aux points dans le cluster le plus proche
Et, = distance moyenne intra-cluster à tous les points.
Indice Davis-Bouldin
L'index DB est une autre bonne métrique pour effectuer l'analyse des algorithmes de clustering. Avec l'aide de l'index DB, nous pouvons comprendre les points suivants sur le modèle de clustering -
Si les grappes sont bien espacées les unes des autres ou non?
Quelle est la densité des grappes?
Nous pouvons calculer l'indice DB à l'aide de la formule suivante -
$DB=\frac{1}{n}\displaystyle\sum\limits_{i=1}^n max_{j\neq{i}}\left(\frac{\sigma_{i}+\sigma_{j}}{d(c_{i},c_{j})}\right)$Ici, = nombre de clusters
σ i = distance moyenne de tous les points du cluster à partir du centre de gravité du cluster.
Moins l'index DB, meilleur est le modèle de clustering.
Index Dunn
Cela fonctionne de la même manière que l'index DB mais il y a des points suivants dans lesquels les deux diffèrent -
L'indice de Dunn ne considère que le pire des cas, c'est-à-dire les clusters qui sont proches les uns des autres, tandis que l'indice DB considère la dispersion et la séparation de tous les clusters dans le modèle de clustering.
L'indice Dunn augmente à mesure que les performances augmentent, tandis que l'indice DB s'améliore lorsque les clusters sont bien espacés et denses.
Nous pouvons calculer l'indice de Dunn à l'aide de la formule suivante -
$D=\frac{min_{1\leq i <{j}\leq{n}}P(i,j)}{mix_{1\leq i < k \leq n}q(k)}$Ici, ,, = chaque index pour les clusters
= distance inter-cluster
q = distance intra-cluster
Types d'algorithmes de clustering ML
Voici les algorithmes de clustering ML les plus importants et les plus utiles -
Clustering K-means
Cet algorithme de clustering calcule les centroïdes et les itère jusqu'à ce que nous trouvions le centroïde optimal. Il suppose que le nombre de clusters est déjà connu. Il est également appelé algorithme de clustering plat. Le nombre de clusters identifiés à partir des données par algorithme est représenté par «K» dans K-means.
Algorithme de décalage moyen
C'est un autre algorithme de clustering puissant utilisé dans l'apprentissage non supervisé. Contrairement au clustering K-means, il ne fait aucune hypothèse, il s'agit donc d'un algorithme non paramétrique.
Classification hiérarchique
C'est un autre algorithme d'apprentissage non supervisé qui est utilisé pour regrouper les points de données non étiquetés ayant des caractéristiques similaires.
Nous discuterons de tous ces algorithmes en détail dans les prochains chapitres.
Applications du clustering
Nous pouvons trouver le clustering utile dans les domaines suivants -
Data summarization and compression- Le clustering est largement utilisé dans les domaines où nous avons également besoin de la synthèse, de la compression et de la réduction des données. Les exemples sont le traitement d'image et la quantification vectorielle.
Collaborative systems and customer segmentation - Le clustering pouvant être utilisé pour trouver des produits similaires ou le même type d'utilisateurs, il peut être utilisé dans le domaine des systèmes collaboratifs et de la segmentation client.
Serve as a key intermediate step for other data mining tasks- L'analyse de cluster peut générer un résumé compact des données pour la classification, le test, la génération d'hypothèses; par conséquent, il sert également d'étape intermédiaire clé pour d'autres tâches d'exploration de données.
Trend detection in dynamic data - Le regroupement peut également être utilisé pour la détection de tendances dans les données dynamiques en créant divers groupes de tendances similaires.
Social network analysis- Le clustering peut être utilisé dans l'analyse des réseaux sociaux. Les exemples génèrent des séquences en images, vidéos ou audios.
Biological data analysis - Le regroupement peut également être utilisé pour créer des grappes d'images, de vidéos, par conséquent, il peut être utilisé avec succès dans l'analyse de données biologiques.
Introduction à l'algorithme K-Means
L'algorithme de clustering K-means calcule les centroïdes et les itère jusqu'à ce que nous trouvions le centroïde optimal. Il suppose que le nombre de clusters est déjà connu. Il est également appeléflat clusteringalgorithme. Le nombre de clusters identifiés à partir des données par algorithme est représenté par «K» dans K-means.
Dans cet algorithme, les points de données sont assignés à un cluster de telle manière que la somme de la distance au carré entre les points de données et le centre de gravité soit minimale. Il faut comprendre qu'une moindre variation au sein des clusters conduira à des points de données plus similaires au sein du même cluster.
Fonctionnement de l'algorithme K-Means
Nous pouvons comprendre le fonctionnement de l'algorithme de clustering K-Means à l'aide des étapes suivantes -
Step1 - Tout d'abord, nous devons spécifier le nombre de clusters, K, à générer par cet algorithme.
Step2- Ensuite, sélectionnez aléatoirement K points de données et attribuez chaque point de données à un cluster. En termes simples, classez les données en fonction du nombre de points de données.
Step3 - Il va maintenant calculer les centres de gravité du cluster.
Step4 - Ensuite, continuez à itérer ce qui suit jusqu'à ce que nous trouvions le centre de gravité optimal qui est l'affectation de points de données aux clusters qui ne changent plus -
4.1 - Tout d'abord, la somme de la distance au carré entre les points de données et les centres de gravité serait calculée.
4.2 - Maintenant, nous devons attribuer chaque point de données au cluster qui est plus proche que l'autre cluster (centroïde).
4.3 - Calculez enfin les centres de gravité des clusters en prenant la moyenne de tous les points de données de ce cluster.
K-means suit Expectation-Maximizationapproche pour résoudre le problème. L'étape d'attente est utilisée pour affecter les points de données au cluster le plus proche et l'étape de maximisation est utilisée pour calculer le centre de gravité de chaque cluster.
Tout en travaillant avec l'algorithme K-means, nous devons prendre soin des choses suivantes -
Tout en travaillant avec des algorithmes de clustering comprenant des K-Means, il est recommandé de normaliser les données car ces algorithmes utilisent la mesure basée sur la distance pour déterminer la similitude entre les points de données.
En raison de la nature itérative des K-Means et de l'initialisation aléatoire des centres de gravité, les K-Means peuvent rester dans un optimum local et ne pas converger vers l'optimum global. C'est pourquoi il est recommandé d'utiliser différentes initialisations des centres de gravité.
Implémentation en Python
Les deux exemples suivants d'implémentation de l'algorithme de clustering K-Means nous aideront à mieux comprendre -
Exemple 1
C'est un exemple simple pour comprendre comment fonctionne k-means. Dans cet exemple, nous allons d'abord générer un jeu de données 2D contenant 4 blobs différents, puis appliquer l'algorithme k-means pour voir le résultat.
Tout d'abord, nous allons commencer par importer les packages nécessaires -
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansLe code suivant générera le 2D, contenant quatre blobs -
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)Ensuite, le code suivant nous aidera à visualiser l'ensemble de données -
plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()
Ensuite, créez un objet de KMeans en fournissant le nombre de clusters, entraînez le modèle et faites la prédiction comme suit -
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)Maintenant, avec l'aide du code suivant, nous pouvons tracer et visualiser les centres du cluster choisis par l'estimateur Python k-means -
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()
Exemple 2
Passons à un autre exemple dans lequel nous allons appliquer le clustering K-means sur un ensemble de données à chiffres simples. K-means essaiera d'identifier des chiffres similaires sans utiliser les informations d'étiquette d'origine.
Tout d'abord, nous allons commencer par importer les packages nécessaires -
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansEnsuite, chargez le jeu de données numériques de sklearn et créez-en un objet. Nous pouvons également trouver le nombre de lignes et de colonnes dans cet ensemble de données comme suit -
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shapeProduction
(1797, 64)La sortie ci-dessus montre que cet ensemble de données contient 1797 échantillons avec 64 fonctionnalités.
Nous pouvons effectuer le clustering comme nous l'avons fait dans l'exemple 1 ci-dessus -
kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shapeProduction
(10, 64)La sortie ci-dessus montre que K-means a créé 10 clusters avec 64 fonctionnalités.
fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)Production
En sortie, nous obtiendrons l'image suivante montrant les centres de clusters appris par k-means.

Les lignes de code suivantes correspondent aux étiquettes de cluster apprises avec les vraies étiquettes qu'elles contiennent -
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]Ensuite, nous pouvons vérifier l'exactitude comme suit -
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Production
0.7935447968836951La sortie ci-dessus montre que la précision est d'environ 80%.
Avantages et inconvénients
Avantages
Voici quelques avantages des algorithmes de clustering K-Means -
Il est très facile à comprendre et à mettre en œuvre.
Si nous avons un grand nombre de variables, les K-moyennes seraient plus rapides que le clustering hiérarchique.
Lors du recalcul des centres de gravité, une instance peut modifier le cluster.
Des clusters plus serrés sont formés avec des K-means par rapport au clustering hiérarchique.
Désavantages
Voici quelques inconvénients des algorithmes de clustering K-Means -
Il est un peu difficile de prévoir le nombre de clusters c'est-à-dire la valeur de k.
La sortie est fortement impactée par les entrées initiales comme le nombre de grappes (valeur de k).
L'ordre des données aura un fort impact sur le résultat final.
Il est très sensible au rééchelonnement. Si nous redimensionnons nos données au moyen de la normalisation ou de la standardisation, la sortie changera complètement.
Il n'est pas bon de faire un travail de clustering si les clusters ont une forme géométrique compliquée.
Applications de l'algorithme de clustering K-Means
Les principaux objectifs de l'analyse de cluster sont:
Pour obtenir une intuition significative à partir des données avec lesquelles nous travaillons.
Cluster-puis-prédire où différents modèles seront construits pour différents sous-groupes.
Pour atteindre les objectifs mentionnés ci-dessus, le clustering K-means fonctionne assez bien. Il peut être utilisé dans les applications suivantes -
Segmentation du marché
Clustering de documents
Segmentation d'image
Compression d'image
Segmentation de la clientèle
Analyser la tendance sur les données dynamiques
Introduction à l'algorithme de décalage moyen
Comme indiqué précédemment, il s'agit d'un autre algorithme de clustering puissant utilisé dans l'apprentissage non supervisé. Contrairement au clustering K-means, il ne fait aucune hypothèse; c'est donc un algorithme non paramétrique.
L'algorithme de décalage moyen assigne essentiellement les points de données aux clusters de manière itérative en déplaçant les points vers la densité de points de données la plus élevée, c'est-à-dire le centre de gravité du cluster.
La différence entre l'algorithme K-Means et Mean-Shift est que plus tard, il n'est pas nécessaire de spécifier le nombre de clusters à l'avance car le nombre de clusters sera déterminé par l'algorithme avec les données.
Fonctionnement de l'algorithme de décalage moyen
Nous pouvons comprendre le fonctionnement de l'algorithme de clustering Mean-Shift à l'aide des étapes suivantes -
Step1 - Commencez par les points de données affectés à leur propre cluster.
Step2 - Ensuite, cet algorithme calculera les centroïdes.
Step3 - Dans cette étape, l'emplacement des nouveaux centres de gravité sera mis à jour.
Step4 - Maintenant, le processus sera itéré et déplacé vers la région de densité plus élevée.
Step5 - Enfin, il sera arrêté une fois que les centres de gravité atteindront la position d'où il ne peut plus bouger.
Implémentation en Python
C'est un exemple simple pour comprendre le fonctionnement de l'algorithme Mean-Shift. Dans cet exemple, nous allons d'abord générer un jeu de données 2D contenant 4 blobs différents, puis appliquer l'algorithme Mean-Shift pour voir le résultat.
%matplotlib inline
import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.datasets.samples_generator import make_blobs
centers = [[3,3,3],[4,5,5],[3,10,10]]
X, _ = make_blobs(n_samples = 700, centers = centers, cluster_std = 0.5)
plt.scatter(X[:,0],X[:,1])
plt.show()
ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
colors = 10*['r.','g.','b.','c.','k.','y.','m.']
for i in range(len(X)):
plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 3)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
marker=".",color='k', s=20, linewidths = 5, zorder=10)
plt.show()Production
[[ 2.98462798 9.9733794 10.02629344]
[ 3.94758484 4.99122771 4.99349433]
[ 3.00788996 3.03851268 2.99183033]]
Estimated clusters: 3
Avantages et inconvénients
Avantages
Voici quelques avantages de l'algorithme de clustering Mean-Shift -
Il n'est pas nécessaire de faire une hypothèse de modèle comme dans K-means ou mélange gaussien.
Il peut également modéliser les clusters complexes qui ont une forme non convexe.
Il n'a besoin que d'un paramètre nommé bande passante qui détermine automatiquement le nombre de clusters.
Il n'y a pas de problème de minima locaux comme dans K-means.
Aucun problème généré par les valeurs aberrantes.
Désavantages
Voici quelques inconvénients de l'algorithme de clustering Mean-Shift -
L'algorithme de décalage moyen ne fonctionne pas bien en cas de dimension élevée, où le nombre de clusters change brusquement.
Nous n'avons aucun contrôle direct sur le nombre de clusters, mais dans certaines applications, nous avons besoin d'un nombre spécifique de clusters.
Il ne peut pas faire la différence entre les modes significatifs et dénués de sens.
Introduction au clustering hiérarchique
Le clustering hiérarchique est un autre algorithme d'apprentissage non supervisé utilisé pour regrouper les points de données non étiquetés ayant des caractéristiques similaires. Les algorithmes de clustering hiérarchique appartiennent aux deux catégories suivantes:
Agglomerative hierarchical algorithms- Dans les algorithmes hiérarchiques agglomératifs, chaque point de données est traité comme un seul cluster, puis fusionne ou agglomère successivement (approche ascendante) les paires de clusters. La hiérarchie des clusters est représentée sous la forme d'un dendrogramme ou d'une structure arborescente.
Divisive hierarchical algorithms - D'autre part, dans les algorithmes hiérarchiques de division, tous les points de données sont traités comme un grand cluster et le processus de clustering implique de diviser (approche descendante) le seul grand cluster en plusieurs petits clusters.
Étapes pour effectuer un clustering hiérarchique agglomératif
Nous allons expliquer le regroupement hiérarchique le plus utilisé et le plus important, c'est-à-dire agglomératif. Les étapes pour effectuer la même chose sont les suivantes -
Step1- Traitez chaque point de données comme un seul cluster. Par conséquent, nous aurons, disons K clusters au début. Le nombre de points de données sera également K au début.
Step2- Maintenant, dans cette étape, nous devons former un grand cluster en joignant deux points de données de placard. Cela se traduira par un total de clusters K-1.
Step3- Maintenant, pour former plus de clusters, nous devons rejoindre deux clusters de placards. Cela se traduira par un total de clusters K-2.
Step4 - Maintenant, pour former un gros cluster, répétez les trois étapes ci-dessus jusqu'à ce que K devienne 0, c'est-à-dire qu'il ne reste plus de points de données à rejoindre.
Step5 - Enfin, après avoir fait un seul gros cluster, les dendrogrammes seront utilisés pour se diviser en plusieurs clusters en fonction du problème.
Rôle des dendrogrammes dans le clustering hiérarchique agglomératif
Comme nous l'avons discuté dans la dernière étape, le rôle du dendrogramme commence une fois que le grand cluster est formé. Le dendrogramme sera utilisé pour diviser les clusters en plusieurs clusters de points de données liés en fonction de notre problème. Il peut être compris à l'aide de l'exemple suivant -
Exemple 1
Pour comprendre, commençons par importer les bibliothèques requises comme suit -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as npEnsuite, nous allons tracer les points de données que nous avons pris pour cet exemple -
X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],])
labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True Position')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom')
plt.show()
À partir du diagramme ci-dessus, il est très facile de voir que nous avons deux clusters dans les points de données, mais dans les données du monde réel, il peut y avoir des milliers de clusters. Ensuite, nous allons tracer les dendrogrammes de nos points de données en utilisant la bibliothèque Scipy -
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
linked = linkage(X, 'single')
labelList = range(1, 11)
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True)
plt.show()
Désormais, une fois le grand cluster formé, la plus longue distance verticale est sélectionnée. Une ligne verticale est ensuite dessinée à travers elle comme indiqué dans le diagramme suivant. Lorsque la ligne horizontale traverse la ligne bleue en deux points, le nombre de grappes serait de deux.

Ensuite, nous devons importer la classe pour le clustering et appeler sa méthode fit_predict pour prédire le cluster. Nous importons la classe AgglomerativeClustering de la bibliothèque sklearn.cluster -
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)Ensuite, tracez le cluster à l'aide du code suivant -
plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')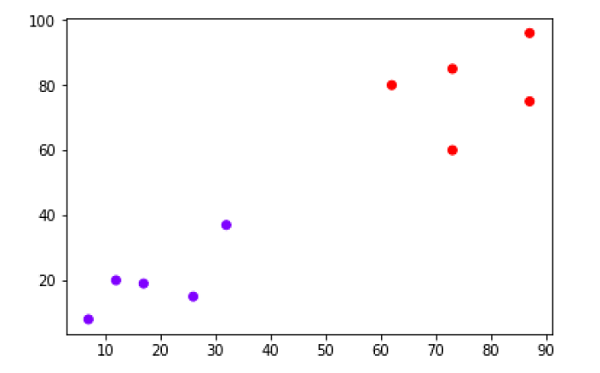
Le diagramme ci-dessus montre les deux clusters de nos points de données.
Exemple2
Comme nous avons compris le concept de dendrogrammes à partir de l'exemple simple discuté ci-dessus, passons à un autre exemple dans lequel nous créons des grappes du point de données dans Pima Indian Diabetes Dataset en utilisant le clustering hiérarchique -
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
import numpy as np
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
data.shape
(768, 9)
data.head()| slno. | preg | Plas | Prés | peau | tester | Masse | pédi | âge | classe |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33,6 | 0,627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26,6 | 0,351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23,3 | 0,672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28,1 | 0,167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43,1 | 2,288 | 33 | 1 |
patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
cluster.fit_predict(patient_data)
plt.figure(figsize=(10, 7))
plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')
introduction
L'algorithme des K-plus proches voisins (KNN) est un type d'algorithme de ML supervisé qui peut être utilisé à la fois pour les problèmes de classification et de prédiction de régression. Cependant, il est principalement utilisé pour les problèmes prédictifs de classification dans l'industrie. Les deux propriétés suivantes définiraient bien KNN -
Lazy learning algorithm - KNN est un algorithme d'apprentissage paresseux car il n'a pas de phase d'apprentissage spécialisée et utilise toutes les données pour l'entraînement lors de la classification.
Non-parametric learning algorithm - KNN est également un algorithme d'apprentissage non paramétrique car il ne suppose rien sur les données sous-jacentes.
Fonctionnement de l'algorithme KNN
L'algorithme des K-plus proches voisins (KNN) utilise la `` similarité des caractéristiques '' pour prédire les valeurs des nouveaux points de données, ce qui signifie en outre que le nouveau point de données se verra attribuer une valeur en fonction de son degré de correspondance avec les points de l'ensemble d'apprentissage. Nous pouvons comprendre son fonctionnement à l'aide des étapes suivantes -
Step1- Pour implémenter n'importe quel algorithme, nous avons besoin d'un ensemble de données. Ainsi, lors de la première étape de KNN, nous devons charger la formation ainsi que les données de test.
Step2- Ensuite, nous devons choisir la valeur de K c'est-à-dire les points de données les plus proches. K peut être n'importe quel entier.
Step3 - Pour chaque point des données de test, procédez comme suit -
3.1- Calculez la distance entre les données de test et chaque ligne de données d'entraînement à l'aide de l'une des méthodes à savoir: distance euclidienne, Manhattan ou Hamming. La méthode la plus couramment utilisée pour calculer la distance est euclidienne.
3.2 - Maintenant, en fonction de la valeur de la distance, triez-les par ordre croissant.
3.3 - Ensuite, il choisira les K premières lignes du tableau trié.
3.4 - Maintenant, il attribuera une classe au point de test en fonction de la classe la plus fréquente de ces lignes.
Step4 - Fin
Exemple
Ce qui suit est un exemple pour comprendre le concept de K et le fonctionnement de l'algorithme KNN -
Supposons que nous ayons un ensemble de données qui peut être tracé comme suit -
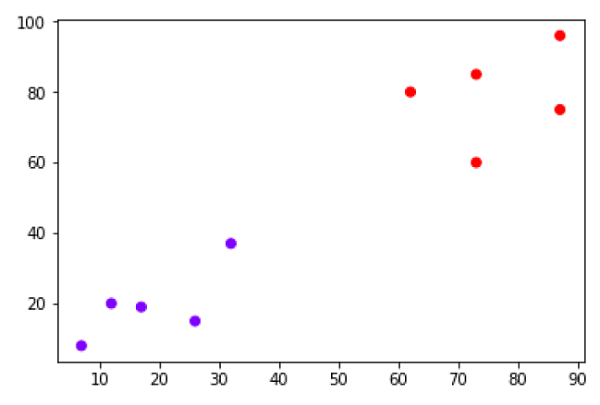
Maintenant, nous devons classer le nouveau point de données avec un point noir (au point 60,60) en classe bleue ou rouge. Nous supposons que K = 3, c'est-à-dire qu'il trouverait trois points de données les plus proches. Il est montré dans le diagramme suivant -

Nous pouvons voir dans le diagramme ci-dessus les trois voisins les plus proches du point de données avec un point noir. Parmi ces trois, deux d'entre eux se trouvent en classe rouge, le point noir sera donc également attribué en classe rouge.
Implémentation en Python
Comme nous le savons, l'algorithme des K-plus proches voisins (KNN) peut être utilisé à la fois pour la classification et la régression. Voici les recettes en Python pour utiliser KNN comme classifieur et régresseur -
KNN comme classificateur
Tout d'abord, commencez par importer les packages Python nécessaires -
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdEnsuite, téléchargez le jeu de données iris à partir de son lien Web comme suit -
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Ensuite, nous devons attribuer des noms de colonne à l'ensemble de données comme suit -
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Maintenant, nous devons lire l'ensemble de données dans le cadre de données pandas comme suit -
dataset = pd.read_csv(path, names=headernames)
dataset.head()| slno. | longueur sépale | largeur sépale | pétale | largeur des pétales | Classe |
|---|---|---|---|---|---|
| 0 | 5.1 | 3,5 | 1,4 | 0,2 | Iris-setosa |
| 1 | 4,9 | 3.0 | 1,4 | 0,2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0,2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1,5 | 0,2 | Iris-setosa |
| 4 | 5,0 | 3,6 | 1,4 | 0,2 | Iris-setosa |
Le prétraitement des données sera effectué à l'aide des lignes de script suivantes -
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].valuesEnsuite, nous diviserons les données en train et test split. Le code suivant divisera l'ensemble de données en 60% de données d'entraînement et 40% de données de test -
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40)Ensuite, la mise à l'échelle des données sera effectuée comme suit -
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Ensuite, entraînez le modèle à l'aide de la classe KNeighborsClassifier de sklearn comme suit -
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=8)
classifier.fit(X_train, y_train)Enfin, nous devons faire des prédictions. Cela peut être fait à l'aide du script suivant -
y_pred = classifier.predict(X_test)Ensuite, imprimez les résultats comme suit -
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Production
Confusion Matrix:
[[21 0 0]
[ 0 16 0]
[ 0 7 16]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 21
Iris-versicolor 0.70 1.00 0.82 16
Iris-virginica 1.00 0.70 0.82 23
micro avg 0.88 0.88 0.88 60
macro avg 0.90 0.90 0.88 60
weighted avg 0.92 0.88 0.88 60
Accuracy: 0.8833333333333333KNN comme régresseur
Tout d'abord, commencez par importer les packages Python nécessaires -
import numpy as np
import pandas as pdEnsuite, téléchargez le jeu de données iris à partir de son lien Web comme suit -
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Ensuite, nous devons attribuer des noms de colonne à l'ensemble de données comme suit -
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Maintenant, nous devons lire l'ensemble de données dans le cadre de données pandas comme suit -
data = pd.read_csv(url, names=headernames)
array = data.values
X = array[:,:2]
Y = array[:,2]
data.shape
output:(150, 5)Ensuite, importez KNeighborsRegressor depuis sklearn pour l'adapter au modèle -
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=10)
knnr.fit(X, y)Enfin, nous pouvons trouver le MSE comme suit -
print ("The MSE is:",format(np.power(y-knnr.predict(X),2).mean()))Production
The MSE is: 0.12226666666666669Avantages et inconvénients de KNN
Avantages
C'est un algorithme très simple à comprendre et à interpréter.
C'est très utile pour les données non linéaires car il n'y a aucune hypothèse sur les données dans cet algorithme.
C'est un algorithme polyvalent car nous pouvons l'utiliser aussi bien pour la classification que pour la régression.
Il a une précision relativement élevée, mais il existe de bien meilleurs modèles d'apprentissage supervisé que KNN.
Les inconvénients
C'est un algorithme un peu coûteux en calcul car il stocke toutes les données d'entraînement.
Stockage de mémoire élevé requis par rapport à d'autres algorithmes d'apprentissage supervisé.
La prédiction est lente en cas de grand N.
Il est très sensible à l'échelle des données ainsi qu'aux fonctionnalités non pertinentes.
Applications de KNN
Voici quelques-uns des domaines dans lesquels KNN peut être appliqué avec succès -
Système bancaire
KNN peut être utilisé dans le système bancaire pour prédire le temps qu'un individu est apte à l'approbation de prêt? Cet individu a-t-il des caractéristiques similaires à celles des défaillants?
Calcul des cotes de crédit
Les algorithmes KNN peuvent être utilisés pour trouver la cote de crédit d'un individu en comparant avec les personnes ayant des traits similaires.
Politique
Avec l'aide des algorithmes KNN, nous pouvons classer un électeur potentiel en différentes classes telles que «votera», «ne votera pas», «votera pour le« congrès »du parti,« votera pour le parti «BJP».
D'autres domaines dans lesquels l'algorithme KNN peut être utilisé sont la reconnaissance vocale, la détection d'écriture manuscrite, la reconnaissance d'image et la reconnaissance vidéo.
Il existe différentes métriques que nous pouvons utiliser pour évaluer les performances des algorithmes de ML, de classification ainsi que des algorithmes de régression. Nous devons choisir soigneusement les métriques pour évaluer les performances du ML car -
La façon dont les performances des algorithmes ML sont mesurées et comparées dépendra entièrement de la métrique que vous choisissez.
La façon dont vous pondérez l'importance de diverses caractéristiques dans le résultat sera entièrement influencée par la métrique que vous choisissez.
Mesures de performance pour les problèmes de classification
Nous avons discuté de la classification et de ses algorithmes dans les chapitres précédents. Ici, nous allons discuter de diverses mesures de performance qui peuvent être utilisées pour évaluer les prédictions des problèmes de classification.
Matrice de confusion
C'est le moyen le plus simple de mesurer les performances d'un problème de classification où la sortie peut être de deux ou plusieurs types de classes. Une matrice de confusion n'est rien d'autre qu'un tableau à deux dimensions, à savoir. "Réel" et "Prévu" et en outre, les deux dimensions ont "Vrais positifs (TP)", "Vrais négatifs (TN)", "Faux positifs (FP)", "Faux négatifs (FN)" comme indiqué ci-dessous -

Les explications des termes associés à la matrice de confusion sont les suivantes -
True Positives (TP) - C'est le cas lorsque la classe réelle et la classe prévue du point de données sont égales à 1.
True Negatives (TN) - C'est le cas lorsque la classe réelle et la classe prévue du point de données sont égales à 0.
False Positives (FP) - C'est le cas lorsque la classe réelle du point de données est 0 et la classe prévue du point de données est 1.
False Negatives (FN) - C'est le cas lorsque la classe réelle du point de données est 1 et la classe prévue du point de données est 0.
Nous pouvons utiliser la fonction confusion_matrix de sklearn.metrics pour calculer la matrice de confusion de notre modèle de classification.
Précision de classification
Il s'agit de la mesure de performance la plus courante pour les algorithmes de classification. Il peut être défini comme le nombre de prédictions correctes faites comme un rapport de toutes les prédictions faites. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$Accuracy =\frac{TP+TN}{+++}$Nous pouvons utiliser la fonction precision_score de sklearn.metrics pour calculer la précision de notre modèle de classification.
Rapport de classification
Ce rapport comprend les scores de Precisions, Recall, F1 et Support. Ils sont expliqués comme suit -
Précision
La précision, utilisée dans les extractions de documents, peut être définie comme le nombre de documents corrects renvoyés par notre modèle ML. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$Precision=\frac{TP}{TP+FP}$Rappel ou sensibilité
Le rappel peut être défini comme le nombre de positifs renvoyés par notre modèle ML. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$Recall =\frac{TP}{TP+FN}$Spécificité
La spécificité, contrairement au rappel, peut être définie comme le nombre de négatifs renvoyés par notre modèle ML. Nous pouvons facilement le calculer par matrice de confusion à l'aide de la formule suivante -
$Specificity =\frac{TN}{TN+FP}$Soutien
La prise en charge peut être définie comme le nombre d'échantillons de la vraie réponse qui se trouve dans chaque classe de valeurs cibles.
Score F1
Cette partition nous donnera le moyen harmonique de précision et de rappel. Mathématiquement, le score F1 est la moyenne pondérée de la précision et du rappel. La meilleure valeur de F1 serait 1 et la pire serait 0. Nous pouvons calculer le score F1 à l'aide de la formule suivante -
= ∗ (∗) / (+)
Le score F1 a une contribution relative égale de précision et de rappel.
Nous pouvons utiliser la fonction classification_report de sklearn.metrics pour obtenir le rapport de classification de notre modèle de classification.
AUC (Aire sous la courbe ROC)
AUC (Area Under Curve) -ROC (Receiver Operating Characteristic) est une mesure de performance, basée sur des valeurs de seuil variables, pour les problèmes de classification. Comme son nom l'indique, ROC est une courbe de probabilité et l'ASC mesure la séparabilité. En termes simples, la métrique AUC-ROC nous renseignera sur la capacité du modèle à distinguer les classes. Plus l'AUC est élevée, meilleur est le modèle.
Mathématiquement, il peut être créé en traçant le TPR (True Positive Rate), c'est-à-dire la sensibilité ou le rappel par rapport au FPR (False Positive Rate), c'est-à-dire la spécificité 1, à différentes valeurs de seuil. Voici le graphique montrant ROC, AUC ayant TPR sur l'axe y et FPR sur l'axe x -

Nous pouvons utiliser la fonction roc_auc_score de sklearn.metrics pour calculer AUC-ROC.
LOGLOSS (perte logarithmique)
Elle est également appelée perte de régression logistique ou perte d'entropie croisée. Il se définit essentiellement sur des estimations de probabilité et mesure la performance d'un modèle de classification où l'entrée est une valeur de probabilité comprise entre 0 et 1. Il peut être compris plus clairement en le différenciant avec précision. Comme nous savons que la précision est le nombre de prédictions (valeur prédite = valeur réelle) dans notre modèle, tandis que la perte logarithmique est le degré d'incertitude de notre prédiction en fonction de son écart par rapport à l'étiquette réelle. Avec l'aide de la valeur Log Loss, nous pouvons avoir une vue plus précise des performances de notre modèle. Nous pouvons utiliser la fonction log_loss de sklearn.metrics pour calculer la perte de journal.
Exemple
Ce qui suit est une recette simple en Python qui nous donnera un aperçu de la façon dont nous pouvons utiliser les mesures de performance expliquées ci-dessus sur le modèle de classification binaire -
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
X_actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
Y_predic = [1, 0, 1, 1, 1, 0, 1, 1, 0, 0]
results = confusion_matrix(X_actual, Y_predic)
print ('Confusion Matrix :')
print(results)
print ('Accuracy Score is',accuracy_score(X_actual, Y_predic))
print ('Classification Report : ')
print (classification_report(X_actual, Y_predic))
print('AUC-ROC:',roc_auc_score(X_actual, Y_predic))
print('LOGLOSS Value is',log_loss(X_actual, Y_predic))Production
Confusion Matrix :
[[3 3]
[1 3]]
Accuracy Score is 0.6
Classification Report :
precision recall f1-score support
0 0.75 0.50 0.60 6
1 0.50 0.75 0.60 4
micro avg 0.60 0.60 0.60 10
macro avg 0.62 0.62 0.60 10
weighted avg 0.65 0.60 0.60 10
AUC-ROC: 0.625
LOGLOSS Value is 13.815750437193334Mesures de performance pour les problèmes de régression
Nous avons discuté de la régression et de ses algorithmes dans les chapitres précédents. Ici, nous allons discuter de diverses mesures de performance qui peuvent être utilisées pour évaluer les prédictions des problèmes de régression.
Erreur absolue moyenne (MAE)
Il s'agit de la mesure d'erreur la plus simple utilisée dans les problèmes de régression. Il s'agit essentiellement de la somme de la moyenne de la différence absolue entre les valeurs prévues et réelles. En termes simples, avec MAE, nous pouvons avoir une idée de la fausseté des prédictions. MAE n'indique pas la direction du modèle, c'est-à-dire aucune indication sur la sous-performance ou la surperformance du modèle. Voici la formule pour calculer MAE -
$MAE = \frac{1}{n}\sum|Y -\hat{Y}|$Ici, = valeurs de sortie réelles
Et $\hat{Y}$= Valeurs de sortie prévues.
Nous pouvons utiliser la fonction mean_absolute_error de sklearn.metrics pour calculer MAE.
Erreur quadratique moyenne (MSE)
MSE est comme le MAE, mais la seule différence est qu'il met au carré la différence des valeurs de sortie réelles et prévues avant de les additionner toutes au lieu d'utiliser la valeur absolue. La différence peut être remarquée dans l'équation suivante -
$MSE = \frac{1}{n}\sum(Y -\hat{Y})$Ici, = valeurs de sortie réelles
Et $\hat{Y}$ = Valeurs de sortie prévues.
Nous pouvons utiliser la fonction mean_squared_error de sklearn.metrics pour calculer MSE.
R au carré (R 2 )
R La métrique au carré est généralement utilisée à des fins explicatives et fournit une indication de la qualité ou de l'ajustement d'un ensemble de valeurs de sortie prédites aux valeurs de sortie réelles. La formule suivante nous aidera à le comprendre -
$R^{2} = 1 -\frac{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\hat{Y_{i}})^2}{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\bar{Y_i)^2}}$Dans l'équation ci-dessus, le numérateur est MSE et le dénominateur est la variance des valeurs.
Nous pouvons utiliser la fonction r2_score de sklearn.metrics pour calculer la valeur R au carré.
Exemple
Ce qui suit est une recette simple en Python qui nous donnera un aperçu de la façon dont nous pouvons utiliser les métriques de performance expliquées ci-dessus sur le modèle de régression -
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
X_actual = [5, -1, 2, 10]
Y_predic = [3.5, -0.9, 2, 9.9]
print ('R Squared =',r2_score(X_actual, Y_predic))
print ('MAE =',mean_absolute_error(X_actual, Y_predic))
print ('MSE =',mean_squared_error(X_actual, Y_predic))Production
R Squared = 0.9656060606060606
MAE = 0.42499999999999993
MSE = 0.5674999999999999introduction
Afin d'exécuter et de produire des résultats avec succès, un modèle d'apprentissage automatique doit automatiser certains flux de travail standard. Le processus d'automatisation de ces flux de travail standard peut être effectué à l'aide de Scikit-learn Pipelines. Du point de vue d'un data scientist, le pipeline est un concept généralisé mais très important. Il permet essentiellement le flux de données de son format brut vers certaines informations utiles. Le fonctionnement des pipelines peut être compris à l'aide du diagramme suivant -

Les blocs de pipelines ML sont les suivants -
Data ingestion- Comme son nom l'indique, il s'agit du processus d'importation des données à utiliser dans le projet ML. Les données peuvent être extraites en temps réel ou par lots à partir de systèmes uniques ou multiples. C'est l'une des étapes les plus difficiles car la qualité des données peut affecter l'ensemble du modèle ML.
Data Preparation- Après avoir importé les données, nous devons préparer les données à utiliser pour notre modèle ML. Le prétraitement des données est l'une des techniques les plus importantes de préparation des données.
ML Model Training- La prochaine étape consiste à former notre modèle ML. Nous avons divers algorithmes ML tels que supervisé, non supervisé, renforcement pour extraire les caractéristiques des données et faire des prédictions.
Model Evaluation- Ensuite, nous devons évaluer le modèle ML. Dans le cas d'un pipeline AutoML, le modèle ML peut être évalué à l'aide de diverses méthodes statistiques et règles métier.
ML Model retraining- Dans le cas d'un pipeline AutoML, il n'est pas nécessaire que le premier modèle soit le meilleur. Le premier modèle est considéré comme un modèle de base et nous pouvons l'entraîner de manière répétée pour augmenter la précision du modèle.
Deployment- Enfin, nous devons déployer le modèle. Cette étape implique l'application et la migration du modèle vers les opérations commerciales pour leur utilisation.
Les défis associés aux pipelines de ML
Afin de créer des pipelines ML, les data scientists sont confrontés à de nombreux défis. Ces défis entrent dans les trois catégories suivantes -
Qualité des données
Le succès de tout modèle ML dépend fortement de la qualité des données. Si les données que nous fournissons au modèle ML ne sont pas précises, fiables et robustes, alors nous allons finir avec une sortie fausse ou trompeuse.
Fiabilité des données
Un autre défi associé aux pipelines ML est la fiabilité des données que nous fournissons au modèle ML. Comme nous le savons, il peut exister diverses sources à partir desquelles le scientifique des données peut acquérir des données, mais pour obtenir les meilleurs résultats, il doit être assuré que les sources de données sont fiables et fiables.
Accessibilité des données
Pour obtenir les meilleurs résultats des pipelines ML, les données elles-mêmes doivent être accessibles, ce qui nécessite la consolidation, le nettoyage et la conservation des données. En raison de la propriété d'accessibilité des données, les métadonnées seront mises à jour avec de nouvelles balises.
Modélisation du pipeline ML et préparation des données
Les fuites de données, qui se produisent du jeu de données d'entraînement au jeu de données de test, sont un problème important pour le scientifique des données lors de la préparation des données pour le modèle ML. Généralement, au moment de la préparation des données, le data scientist utilise des techniques telles que la standardisation ou la normalisation sur l'ensemble de données avant l'apprentissage. Mais ces techniques ne peuvent pas nous aider à éviter les fuites de données car l'ensemble de données d'entraînement aurait été influencé par l'échelle des données dans l'ensemble de données de test.
En utilisant des pipelines ML, nous pouvons empêcher cette fuite de données, car les pipelines garantissent que la préparation des données comme la normalisation est limitée à chaque volet de notre procédure de validation croisée.
Exemple
Voici un exemple en Python qui illustre le workflow de préparation des données et d'évaluation de modèle. À cette fin, nous utilisons l'ensemble de données Pima Indian Diabetes de Sklearn. Premièrement, nous créerons un pipeline qui normalisera les données. Ensuite, un modèle d'analyse discriminante linéaire sera créé et enfin le pipeline sera évalué en utilisant une validation croisée de 10 fois.
Tout d'abord, importez les packages requis comme suit -
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.discriminant_analysis import LinearDiscriminantAnalysisMaintenant, nous devons charger l'ensemble de données sur le diabète Pima comme dans les exemples précédents -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.valuesEnsuite, nous allons créer un pipeline à l'aide du code suivant -
estimators = []
estimators.append(('standardize', StandardScaler()))
estimators.append(('lda', LinearDiscriminantAnalysis()))
model = Pipeline(estimators)Enfin, nous allons évaluer ce pipeline et afficher sa précision comme suit -
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Production
0.7790148448043184La sortie ci-dessus est le résumé de la précision de la configuration sur l'ensemble de données.
Modélisation du pipeline ML et de l'extraction de fonctionnalités
Des fuites de données peuvent également se produire à l'étape d'extraction de caractéristiques du modèle ML. C'est pourquoi les procédures d'extraction d'entités doivent également être limitées pour arrêter les fuites de données dans notre ensemble de données d'entraînement. Comme dans le cas de la préparation des données, en utilisant des pipelines ML, nous pouvons également empêcher cette fuite de données. FeatureUnion, un outil fourni par les pipelines ML peut être utilisé à cet effet.
Example
The following is an example in Python that demonstrates feature extraction and model evaluation workflow. For this purpose, we are using Pima Indian Diabetes dataset from Sklearn.
First, 3 features will be extracted with PCA (Principal Component Analysis). Then, 6 features will be extracted with Statistical Analysis. After feature extraction, result of multiple feature selection and extraction procedures will be combined by using
FeatureUnion tool. At last, a Logistic Regression model will be created, and the pipeline will be evaluated using 10-fold cross validation.
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.pipeline import FeatureUnion
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
from sklearn.feature_selection import SelectKBestNow, we need to load the Pima diabetes dataset as did in previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.valuesNext, feature union will be created as follows −
features = []
features.append(('pca', PCA(n_components=3)))
features.append(('select_best', SelectKBest(k=6)))
feature_union = FeatureUnion(features)Next, pipeline will be creating with the help of following script lines −
estimators = []
estimators.append(('feature_union', feature_union))
estimators.append(('logistic', LogisticRegression()))
model = Pipeline(estimators)At last, we are going to evaluate this pipeline and output its accuracy as follows −
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Output
0.7789811066126855The above output is the summary of accuracy of the setup on the dataset.
Performance Improvement with Ensembles
Ensembles can give us boost in the machine learning result by combining several models. Basically, ensemble models consist of several individually trained supervised learning models and their results are merged in various ways to achieve better predictive performance compared to a single model. Ensemble methods can be divided into following two groups −
Sequential ensemble methods
As the name implies, in these kind of ensemble methods, the base learners are generated sequentially. The motivation of such methods is to exploit the dependency among base learners.
Parallel ensemble methods
As the name implies, in these kind of ensemble methods, the base learners are generated in parallel. The motivation of such methods is to exploit the independence among base learners.
Ensemble Learning Methods
The following are the most popular ensemble learning methods i.e. the methods for combining the predictions from different models −
Bagging
The term bagging is also known as bootstrap aggregation. In bagging methods, ensemble model tries to improve prediction accuracy and decrease model variance by combining predictions of individual models trained over randomly generated training samples. The final prediction of ensemble model will be given by calculating the average of all predictions from the individual estimators. One of the best examples of bagging methods are random forests.
Boosting
In boosting method, the main principle of building ensemble model is to build it incrementally by training each base model estimator sequentially. As the name suggests, it basically combine several week base learners, trained sequentially over multiple iterations of training data, to build powerful ensemble. During the training of week base learners, higher weights are assigned to those learners which were misclassified earlier. The example of boosting method is AdaBoost.
Voting
In this ensemble learning model, multiple models of different types are built and some simple statistics, like calculating mean or median etc., are used to combine the predictions. This prediction will serve as the additional input for training to make the final prediction.
Bagging Ensemble Algorithms
The following are three bagging ensemble algorithms −
Bagged Decision Tree
As we know that bagging ensemble methods work well with the algorithms that have high variance and, in this concern, the best one is decision tree algorithm. In the following Python recipe, we are going to build bagged decision tree ensemble model by using BaggingClassifier function of sklearn with DecisionTreeClasifier (a classification & regression trees algorithm) on Pima Indians diabetes dataset.
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifierNow, we need to load the Pima diabetes dataset as we did in the previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Next, give the input for 10-fold cross validation as follows −
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
cart = DecisionTreeClassifier()We need to provide the number of trees we are going to build. Here we are building 150 trees −
num_trees = 150Next, build the model with the help of following script −
model = BaggingClassifier(base_estimator=cart, n_estimators=num_trees, random_state=seed)Calculate and print the result as follows −
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Output
0.7733766233766234The output above shows that we got around 77% accuracy of our bagged decision tree classifier model.
Random Forest
It is an extension of bagged decision trees. For individual classifiers, the samples of training dataset are taken with replacement, but the trees are constructed in such a way that reduces the correlation between them. Also, a random subset of features is considered to choose each split point rather than greedily choosing the best split point in construction of each tree.
In the following Python recipe, we are going to build bagged random forest ensemble model by using RandomForestClassifier class of sklearn on Pima Indians diabetes dataset.
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifierNow, we need to load the Pima diabetes dataset as did in previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Next, give the input for 10-fold cross validation as follows −
seed = 7
kfold = KFold(n_splits=10, random_state=seed)We need to provide the number of trees we are going to build. Here we are building 150 trees with split points chosen from 5 features −
num_trees = 150
max_features = 5Next, build the model with the help of following script −
model = RandomForestClassifier(n_estimators=num_trees, max_features=max_features)Calculate and print the result as follows −
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Output
0.7629357484620642The output above shows that we got around 76% accuracy of our bagged random forest classifier model.
Extra Trees
It is another extension of bagged decision tree ensemble method. In this method, the random trees are constructed from the samples of the training dataset.
In the following Python recipe, we are going to build extra tree ensemble model by using ExtraTreesClassifier class of sklearn on Pima Indians diabetes dataset.
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifierNow, we need to load the Pima diabetes dataset as did in previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Next, give the input for 10-fold cross validation as follows −
seed = 7
kfold = KFold(n_splits=10, random_state=seed)We need to provide the number of trees we are going to build. Here we are building 150 trees with split points chosen from 5 features −
num_trees = 150
max_features = 5Next, build the model with the help of following script −
model = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)Calculate and print the result as follows −
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Output
0.7551435406698566The output above shows that we got around 75.5% accuracy of our bagged extra trees classifier model.
Boosting Ensemble Algorithms
The followings are the two most common boosting ensemble algorithms −
AdaBoost
It is one the most successful boosting ensemble algorithm. The main key of this algorithm is in the way they give weights to the instances in dataset. Due to this the algorithm needs to pay less attention to the instances while constructing subsequent models.
In the following Python recipe, we are going to build Ada Boost ensemble model for classification by using AdaBoostClassifier class of sklearn on Pima Indians diabetes dataset.
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifierNow, we need to load the Pima diabetes dataset as did in previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Next, give the input for 10-fold cross validation as follows −
seed = 5
kfold = KFold(n_splits=10, random_state=seed)We need to provide the number of trees we are going to build. Here we are building 150 trees with split points chosen from 5 features −
num_trees = 50Next, build the model with the help of following script −
model = AdaBoostClassifier(n_estimators=num_trees, random_state=seed)Calculate and print the result as follows −
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Output
0.7539473684210527The output above shows that we got around 75% accuracy of our AdaBoost classifier ensemble model.
Stochastic Gradient Boosting
It is also called Gradient Boosting Machines. In the following Python recipe, we are going to build Stochastic Gradient Boostingensemble model for classification by using GradientBoostingClassifier class of sklearn on Pima Indians diabetes dataset.
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifierNow, we need to load the Pima diabetes dataset as did in previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Next, give the input for 10-fold cross validation as follows −
seed = 5
kfold = KFold(n_splits=10, random_state=seed)We need to provide the number of trees we are going to build. Here we are building 150 trees with split points chosen from 5 features −
num_trees = 50Next, build the model with the help of following script −
model = GradientBoostingClassifier(n_estimators=num_trees, random_state=seed)Calculate and print the result as follows −
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Output
0.7746582365003418The output above shows that we got around 77.5% accuracy of our Gradient Boosting classifier ensemble model.
Voting Ensemble Algorithms
As discussed, voting first creates two or more standalone models from training dataset and then a voting classifier will wrap the model along with taking the average of the predictions of sub-model whenever needed new data.
In the following Python recipe, we are going to build Voting ensemble model for classification by using VotingClassifier class of sklearn on Pima Indians diabetes dataset. We are combining the predictions of logistic regression, Decision Tree classifier and SVM together for a classification problem as follows −
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifierNow, we need to load the Pima diabetes dataset as did in previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Ensuite, donnez l'entrée pour la validation croisée 10 fois comme suit -
kfold = KFold(n_splits=10, random_state=7)Ensuite, nous devons créer des sous-modèles comme suit -
estimators = []
model1 = LogisticRegression()
estimators.append(('logistic', model1))
model2 = DecisionTreeClassifier()
estimators.append(('cart', model2))
model3 = SVC()
estimators.append(('svm', model3))Maintenant, créez le modèle d'ensemble de vote en combinant les prédictions des sous-modèles créés ci-dessus.
ensemble = VotingClassifier(estimators)
results = cross_val_score(ensemble, X, Y, cv=kfold)
print(results.mean())Production
0.7382262474367738La sortie ci-dessus montre que nous avons obtenu une précision d'environ 74% de notre modèle d'ensemble de classificateurs de vote.
Amélioration des performances avec le réglage d'algorithme
Comme nous le savons, les modèles ML sont paramétrés de manière à ce que leur comportement puisse être ajusté pour un problème spécifique. Le réglage de l'algorithme signifie trouver la meilleure combinaison de ces paramètres afin que les performances du modèle ML puissent être améliorées. Ce processus parfois appelé optimisation des hyperparamètres et les paramètres de l'algorithme lui-même sont appelés hyperparamètres et les coefficients trouvés par l'algorithme ML sont appelés paramètres.
Ici, nous allons discuter de certaines méthodes de réglage des paramètres d'algorithme fournies par Python Scikit-learn.
Réglage des paramètres de recherche de grille
C'est une approche de réglage des paramètres. Le point clé du fonctionnement de cette méthode est qu'elle construit et évalue le modèle méthodiquement pour chaque combinaison possible de paramètre d'algorithme spécifié dans une grille. Par conséquent, nous pouvons dire que cet algorithme a un caractère de recherche.
Exemple
Dans la recette Python suivante, nous allons effectuer une recherche de grille en utilisant la classe GridSearchCV de sklearn pour évaluer diverses valeurs alpha pour l'algorithme de régression Ridge sur l'ensemble de données sur le diabète des Indiens Pima.
Tout d'abord, importez les packages requis comme suit -
import numpy
from pandas import read_csv
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCVMaintenant, nous devons charger l'ensemble de données sur le diabète Pima comme dans les exemples précédents -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Ensuite, évaluez les différentes valeurs alpha comme suit -
alphas = numpy.array([1,0.1,0.01,0.001,0.0001,0])
param_grid = dict(alpha=alphas)Maintenant, nous devons appliquer la recherche de grille sur notre modèle -
model = Ridge()
grid = GridSearchCV(estimator=model, param_grid=param_grid)
grid.fit(X, Y)Imprimez le résultat avec la ligne de script suivante -
print(grid.best_score_)
print(grid.best_estimator_.alpha)Production
0.2796175593129722
1.0Le résultat ci-dessus nous donne le score optimal et l'ensemble des paramètres de la grille qui ont atteint ce score. La valeur alpha dans ce cas est de 1,0.
Réglage des paramètres de recherche aléatoire
C'est une approche de réglage des paramètres. Le point clé du fonctionnement de cette méthode est qu'elle échantillonne les paramètres de l'algorithme à partir d'une distribution aléatoire pour un nombre fixe d'itérations.
Exemple
Dans la recette Python suivante, nous allons effectuer une recherche aléatoire en utilisant la classe RandomizedSearchCV de sklearn pour évaluer différentes valeurs alpha entre 0 et 1 pour l'algorithme de régression Ridge sur l'ensemble de données sur le diabète des Indiens Pima.
Tout d'abord, importez les packages requis comme suit -
import numpy
from pandas import read_csv
from scipy.stats import uniform
from sklearn.linear_model import Ridge
from sklearn.model_selection import RandomizedSearchCVMaintenant, nous devons charger l'ensemble de données sur le diabète Pima comme dans les exemples précédents -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Ensuite, évaluez les différentes valeurs alpha sur l'algorithme de régression Ridge comme suit -
param_grid = {'alpha': uniform()}
model = Ridge()
random_search = RandomizedSearchCV(estimator=model, param_distributions=param_grid, n_iter=50,
random_state=7)
random_search.fit(X, Y)Imprimez le résultat avec la ligne de script suivante -
print(random_search.best_score_)
print(random_search.best_estimator_.alpha)Production
0.27961712703051084
0.9779895119966027
0.9779895119966027La sortie ci-dessus nous donne le score optimal tout simplement similaire à la recherche de grille.