Raisonnement - Horloge
Les aiguilles d'une horloge peuvent avoir un angle maximum de 180 o entre elles. Lorsque cela se produit, les deux mains représentent une ligne droite.
Les aiguilles d'une horloge font des angles droits deux fois par heure lorsqu'elles sont à 15 minutes l'une de l'autre.
Les deux aiguilles d'une horloge coïncident une fois toutes les heures.
Une horloge est très essentielle pour que chaque être humain puisse planifier ses tâches quotidiennes. La théorie de l'horloge est liée à la vie quotidienne.
Une horloge est un instrument qui affiche l'heure en la divisant en heures, minutes et secondes.
Cadran
Il a un cadran circulaire numéroté de 1 à 12 qui indique les heures. La circonférence d'un cadran est divisée en 60 espaces égaux, appelés espaces des minutes.
1 heure = 60 minutes
1 minute = 60 secondes et
1 heure = 3600 secondes
Des trucs
Entre n et (n + 1) heures, les deux aiguilles d'une horloge coïncideront à $ \ left (\ frac {60n} {11} \ right) $ min après n.
Entre n et (n + 1) heures, les deux aiguilles d'une horloge feront mutuellement un angle droit à $ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} $ min après n .
Entre n et (n + 1) heures, les aiguilles d'une horloge seront en ligne droite (sans être ensemble) à
$ \ left (5n - 30 \ right) \ times \ frac {12} {11} $ min après n, (quand n> 6)
$ \ left (5n + 30 \ right) \ times \ frac {12} {11} $ min après n, (quand n <6)
Entre n et (n + 1) heures, les aiguilles d'une horloge sont espacées de $ x $ min à $ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $ min après n. Le signe «+» indique que l'aiguille des minutes est en avance et le signe «-» indique que l'aiguille des heures est en avance.
Si l'aiguille des minutes d'une horloge dépasse l'aiguille des heures à un intervalle de $ x $ min de l'heure correcte, alors l'horloge perd ou gagne de $ \ left (\ frac {720} {11} - x \ right) \ left (\ frac {60 \ times 24} {x} \ right) $ min.
1 - A quelle heure entre 7h15 et 8h15, les aiguilles d'une horloge coïncideront?
Options -
A - 39 $ \ frac {5} {11} $
B - 39 $ \ frac {4} {11} $
C - 38 $ \ frac {5} {11} $
D - 39 $ \ frac {4} {11} $
Answer - Un
Explanation -
$ \ frac {60 \ times n} {11} = \ frac {60} {11} \ times \ frac {29} {4} = 39 \ frac {5} {11} $
Où $ n = 7,15 = 7 \ frac {15} {60} = \ frac {29} {4} $
2 - A quelle heure particulière, entre 9 et 8 heures, les deux aiguilles seront à angle droit l'une par rapport à l'autre?
Options -
A - 65 $ \ frac {4} {11} $ et 32 $ \ frac {7} {11} $ min après 9
B - 65 $ \ frac {2} {11} $ et 32 $ \ frac {2} {11} $ min après 9
C - 65 $ \ frac {3} {11} $ et 32 $ \ frac {3} {11} $ min après 9
D - 65 $ \ frac {1} {11} $ et 32 $ \ frac {1} {11} $ min après 9
Answer - Un
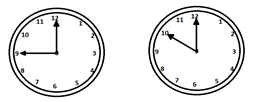
Explanation -
$ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} = \ left (5 \ times9 \ pm 15 \ right) \ times \ frac {12} {11} $
$ = 65 \ frac {4} {11} $ et $ 32 \ frac {7} {11} $ min après 9
3 - Entre 12 et 1 heures, quand les deux aiguilles d'une horloge formeront-elles une ligne droite?
Options -
A- $ \ frac {360} {11} $ min. 12 passé
B- $ \ frac {355} {11} $ min. 12 passé
C- $ \ frac {340} {11} $ min. 12 passé
D- $ \ frac {345} {11} $ min. 12 passé
Answer - D
Explanation -
$ \ left (5n-30 \ right) \ times \ frac {12} {11} $ min après n
$ \ left (6-30 \ right) \ times \ frac {12} {11} $ min. 12 passé
$ = \ frac {345} {11} $ min. 12 dernières (puisque n = 12)
4- Dans combien de temps, les aiguilles d'une horloge seront dans les 30 min. espace à part quand ils sont entre 12 et 13 heures le lundi?
Options -
A - $ \ frac {1080} {11} $ et $ \ frac {300} {11} $ min après 12
B - $ \ frac {1080} {12} $ et $ \ frac {360} {11} $ min après 12
C - $ \ frac {1080} {11} $ et $ \ frac {360} {11} $ min après 12
D - $ \ frac {1080} {12} $ et $ \ frac {300} {12} $ min après 12
Answer - C
Explanation -
$ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $
$ = \ left (5 \ times12 \ pm 30 \ right) \ times \ frac {12} {11} $
$ = \ frac {90 \ times12} {11} $ et $ \ frac {30 \ times12} {11} $ min après 12 = $ \ frac {1080} {11} $ et $ \ frac {360} {11} $ min après 12
5- L'aiguille des minutes d'une horloge dépasse l'aiguille des heures à intervalle de 61 min. puis l'horloge perd ou gagne de combien de temps?
Options -
A - 104 $ \ frac {4} {671} $ min.
B - 105 $ \ frac {1} {671} $ min.
C - 104 $ \ frac {3} {671} $ min.
D - 105 $ \ frac {4} {671} $ min.
Answer - B
Explanation -
$ \ left (\ frac {720} {11} -61 \ right) \ times \ left (\ frac {60 \ times24} {61} \ right) $
$ = 105 \ frac {1} {671} $ min.