Raisonnement - Nombres binaires codés
Le nombre qui a la base 2 est appelé nombre binaire. Le nombre binaire est composé de compléments de 0 et de 1. Ainsi, le nombre binaire codé se compose de deux processus. L'un est la conversion de binaire en décimal et un autre est de décimal en binaire.
Nombres décimaux
Savoir quoi binary numberest, nous devons d'abord connaître les nombres décimaux. Ainsi, le nombre décimal se compose de dix chiffres (c'est-à-dire 0,1,2,3,4,5,6,7,8,9). Tout système décimal peut être représenté en utilisant ces nombres. Par exemple, une séquence de chiffres est 2, 4, 6 et 8. Nous le faisons de la manière suivante -
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- On obtient la valeur des nombres dans ce cas en multipliant les différents chiffres de séquence par des puissances de 10 et en ajoutant. Ici, ce 10 est appelé base ou radix. Par conséquent, sous un système décimal, notre base est de 10.
Nombres binaires
Nous utilisons dix chiffres pour représenter un decimal number; comme ça, nous n'utilisons que deux chiffres pour représenter un nombre binaire. N'importe quel nombre peut être représenté en utilisant ces deux chiffres, c'est-à-dire 0 et 1.
Exemple de nombre binaire: 1101. Ici, 4 chiffres sont présents dans la séquence de chiffres - 1, 1, 0, 1. Nous obtenons la valeur de la manière suivante.
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
Ainsi, le nombre binaire représente treize en système décimal. La valeur peut être déterminée parmultiplying different digits de séquence par puissances de 2 et addition.
Conventional method - Dans l'exemple ci-dessus, nous voyons que pour obtenir la valeur de n'importe quel nombre binaire, nous utilisons la règle suivante -
Le premier chiffre à partir de la droite est multiplié par 2 0 = 1
Le deuxième chiffre à partir de la droite est multiplié par 2 1 = 2
Le troisième chiffre à partir de la droite est multiplié par 2 2 = 4
De même, le n ième chiffre à partir de la droite est multiplié par 2 n − 1
Enfin, tout cela est ajouté.
For Example - Convertissez les nombres binaires suivants en nombres décimaux.
A - 1010
B - 1111
C - 100
D - 10000
Solution -
A - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
B - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
C - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
D - 10000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
Méthode plus rapide
Step I- En partant du chiffre droit du nombre donné, écrivez 1, 2, 4, 8, 16, 32 ……. et ainsi de suite sous chaque chiffre tandis que vous avancez vers la gauche.
Step II- Ignorez les nombres inférieurs à 0. Additionnez tous les nombres inférieurs à 1.
Résolvons l'exemple 1 par cette méthode.
A - 1010
Nous utiliserons 1,2,4,8 car ici 4 chiffres sont présents.
On a,
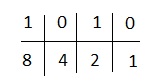
4 et 1 tombent sous les zéros. Nous les ignorons et ajoutons le reste. Nous obtenons 8 + 2 = 10
Comme ça, nous pouvons résoudre d'autres nombres.
Le nombre décimal peut être converti en binaire par la méthode de successive divisions. Chaque fois de division, le dividende est divisé par 2. Le rappel est noté et le quotient devient le dividende suivant, qui est à nouveau divisé par 2. Le processus est répété jusqu'à ce qu'il ne soit plus possible de division.
Par exemple - convertir 17 en nombre binaire -
Divisez 17 par 2 jusqu'à ce qu'il n'y ait plus de division possible.
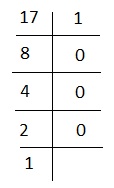
Ainsi, la forme binaire de 17 est 10001.
Direction (Q. 1-4) − Study the following question and give the answer.
Dans un certain code, le symbole pour 0 est + et pour 1 est #. Aucun nombre ou symbole n'est supérieur à 1. La valeur du symbole pour 1 se double à chaque fois qu'il se déplace d'une place vers la gauche.
'0' est représenté par +
'1' est représenté par #
'2' est représenté par # +
'3' est représenté par ##
'4' est représenté par # ++ et ainsi de suite
1 - Lequel des éléments suivants représentera 11?
Options -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - aucun d'eux
Answer - Option A
Explanation - Pour obtenir l'équivalent de 11, on utilise la méthode de division successive par 2.

La forme binaire sera donc 10111. En remplaçant 1 et 0 par # et +, nous obtiendrons # + ##.
2 - Lequel des éléments suivants représentera 8?
Options -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - aucun d'eux
Answer - Option E
Explanation - pour 8, nous avons-
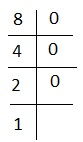
c'est-à-dire 1000 ou # +++. Le bon choix est 5.
3 - Lequel des éléments suivants sera représenté par ## + #?
Options -
A - 8
B - 11
C - 13
D - 12
E - aucun d'eux
Answer - Option E
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 15
4 - Lequel des nombres suivants sera représenté par # +++ #?
Options -
A - 22
B - 31
C - 14
D - 17
E - aucun d'eux
Answer - Option D
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
Les systèmes binaires ont la base 2, un système décimal a la base 10 et le système tertiaire a la base 3, tandis que le système octal a la base 8. Dans le cas du tertiaire, nous avons trois chiffres pour représenter les nombres. Ce sont 0, 1 et 2. Dans ce cas, les nombres seront convertis en nombres décimaux en multipliant avec les puissances appropriées de 3.
For Example -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3