Raisonnement - Syllogisme
Le sens du syllogisme donné par les Grecs est Deduction. C'est une sorte d'argumentation logique.
Définition de quelques termes importants
Il y a quelques termes donnés ci-dessous qui ont un rôle important dans la résolution de problèmes sur le syllogisme.
Proposition- la proposition est une phrase qui fait des déclarations. La proposition se compose de 3 parties: a) sujet, b) prédicat et c) relation entre sujet et prédicat. Quelques propositions sont données ci-dessous.
- Toutes les côtes sont des plages.
- Aucun étudiant n'est honnête.
- Certains documents sont secrets.
Subject and Predicate- Le sujet est cette partie sur laquelle quelque chose est dit. Par contre, le prédicat est la partie qui est liée au sujet. Par exemple - à partir des propositions ci-dessus, les côtes, les étudiants, les documents sont des sujets tandis que les plages, l'honnêteté et le secret sont des prédicats.
Types de proposition catégorielle
Universal Proposition- La proposition universelle est celle qui, soit inclut entièrement le sujet, soit l'exclut entièrement. Par exemple, aucun étudiant n'est intelligent. La proposition universelle est en outre classée comme suit -
Universal positive proposition - Lorsque le formulaire est all X are Yalors cela s'appelle proposition positive. Il est généralement désigné par lettreA.
Universal negative proposition - Lorsque le formulaire est no X are T, alors il est appelé comme proposition négative. Il est désigné parE.
Particular proposition- C'est la proposition qui montre le sujet partiellement ou l'exclut partiellement mais pas complètement. Par exemple, certains chats sont en coton. Il est également divisé en types suivants -
Particular positive proposition - Formulaires comme some X are Usont appelées proposition positive particulière. Ils sont codés commeI.
Particular negative proposition - Formulaires comme Some T are not P par exemple, some cats are not coils est appelée proposition négative particulière et codée comme O.
Mediate inference- Ici, la conclusion est tirée de deux déclarations. Exemple - «toutes les lèvres sont des bobines» et «toutes les balles sont des chauves-souris». La conclusion sera donc «toutes les lèvres sont des bobines».
Immediate inference- Ici, la conclusion sera tirée d'une seule proposition. Par exemple, si la déclaration est «tous les enseignants sont dieu», alors la conclusion sera «certains enseignants sont dieu».
Deux méthodes importantes d'inférence immédiate
Ces méthodes comprennent la conversion, la contraposition, etc.
Implications- Supposons que «tous les chats sont des plages», cela montre que la conclusion «certains chats sont des plages» est vraie. Donc, si une proposition donnée est de catégorie A, cela montre également que la conclusion de type I doit être vraie.
Conversion - Il se compose de 2 étapes.
Step 1 - Le sujet sera converti en prédicat et vice versa.
Step 2 - La proposition qui est donnée sera modifiée en conséquence.
For Example −
Statements- Tous les chats sont des casiers. Tous les sacs sont des étagères. Certains sacs à main sont des sacs.
Conclusions -
1. Certains chats sont des sacs.
2. Certains supports sont des chats.
3. Certains supports sont des sacs à main.
A - Seulement 1
B - Seulement 2 et 3
C - Seulement 1 et 2
D - Seulement 1 et 3
Solution −
Réponse - Option B
La manière picturale de représenter les propositions est formulée par Euler. La relation peut être établie de quatre manières selon quatre propositions.
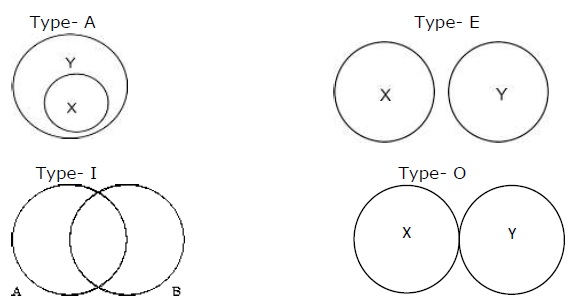
Type - A signifie «Tous les X sont Y», Type - E signifie «Aucun X n'est Y», Type - I signifie «Certains A sont B» et Type - O signifie «Certains X ne sont pas Y».
For Example −
Statements −Certains appareils photo sont des ordinateurs portables.
Certains ordinateurs portables sont des téléphones.
Certains téléphones sont des tablettes.
Conclusions −
I - Au moins certaines tablettes sont des caméras
II - Il est possible que toutes les tablettes soient des ordinateurs portables
III - Aucune des tablettes n'est un ordinateur portable
Solution −
Diagramme circulaire -
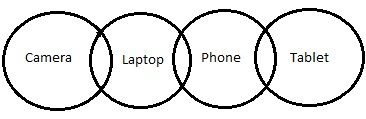
Selon le diagramme ci-dessus,
La conclusion III suit. Mais le mot «possibilité» a été mentionné dans la déclaration. Alors vérifions les possibilités.
Le nouveau diagramme sera -
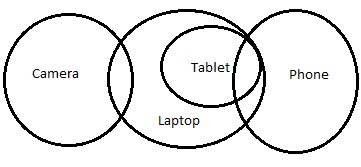
Mais dans ce cas, la conclusion III ne suit pas. La conclusion II ou la conclusion III suit.