Raisonnement - Cube et cuboïde
De nos jours, des questions basées sur les «cubes et cuboïdes» sont posées dans presque tous les concours. Ces problèmes sont très fréquents dans divers concours.
Les méthodes décrites ci-dessous sont simples mais élégantes. Ils devraient être très faciles à comprendre et avec un peu de pratique, vous devriez les maîtriser. Un cube est un solide tridimensionnel ayant 6 faces, 12 arêtes et coins. Tous les bords d'un cube sont égaux et toutes les faces sont de forme carrée. C'est une figure solide qui a 6 faces; chaque face étant un carré est appeléea cube. Si chacune des six faces est un rectangle, il est appelécuboid. Un cuboïde est également appelé unrectangular parallelepiped.
Les questions posées sur le cube et les cuboïdes peuvent être des types suivants.
Type I
Plusieurs vues d'un cube complet sont données et vous devez trouver quelle partie du cube se trouve exactement en dessous d'une partie particulière.
Type II
Un cube ouvert est donné et vous devez prédire à quoi il ressemblera lorsqu'il sera fermé dans un cube.
Type III
Un cube ne pouvait pas être verni sur ou certaines de ses faces avec la même couleur ou des couleurs différentes, puis découpé en un certain nombre spécifié de pièces identiques. Puis question de la forme - "combien de petits cubes ont 2 faces vernies?" "Combien de petits cubes ont une seule face vernie?" etc.
Il existe deux types de problèmes qui apparaissent à l'examen. Au début, vous obtenez plusieurs vues d'uncomplete cube, et vous devez indiquer quelle partie du cube se trouve exactement sous une partie particulière. Dans un autre type, on vous donne unopened-up cube, et vous devez prédire à quoi il ressemblera lorsqu'il sera fermé dans un cube.
For Example -
Plusieurs faces d'un cube sont illustrées ci-dessous -

Quel nombre serait opposé à 2?
A - 1
B - 6
C - 5
D - 4
L'approche fondamentale est la suivante -
Type I
A fundamental rule: Opposite cannot be together;
Chaque fois que nous voyons un cube, avec seulement trois de ses faces visibles pour nous, nous ne pouvons jamais voir deux faces opposées ensemble. Avec toutes ces règles, nous pouvons facilement résoudre le type de problème discuté ci-dessus. Dans la question ci-dessus où nous devons trouver la face opposée d'une face particulière, nous pouvons éliminer les faces qui se sont produites avec X dans n'importe quelle vue. Ainsi, nous pouvons éliminer tout autre choix et rester sera notre réponse.
À ce stade, vous devriez revoir le paragraphe précédent et voir que vous comprenez le concept. Après cela, vous devriez essayer de résoudre l'exemple ci-dessus et voir si vous pouvez appliquer le concept discuté ci-dessus. Cependant, vous constatez que vous n'avez pas entièrement compris le concept, pas de problème. Continuez à lire cette section. Les choses deviendront claires une fois que vous aurez terminé la section. Avec la règle fondamentale ci-dessus au fond de votre esprit, vous pouvez résoudre le type de question ci-dessus.
Pour la question, la règle suffit en elle-même. Après cela, vous pouvez le résoudre plus rapidement enthree secondary rules.
Solution for above example -
Dans l'exemple donné, nous devons trouver la face opposée 2. Maintenant, sur la première figure, 2 apparaît avec 1 et 3. Cela signifie que ni 1 ni 3 ne peuvent être opposés à 2. Cela signifie que l'opposé de 1 nous pouvons avoir 4 ou 5 ou 6. De même, en face de 3, nous pouvons avoir 4 ou 5 ou 6. Maintenant, regardez le deuxième chiffre. Ici, 3 et 1 se produisent en même temps que 5. Cela signifie que 5 est opposé à ni 3 ni 1. Donc, cela signifie que 4 ou 6 est opposé à 1 et l'autre est opposé à 3 donc 5 doit être opposé 2. Donc 5 est correct répondre.
Quelques règles plus rapides
Vous devez maintenant avoir compris l'astuce de base pour résoudre de telles questions. L'astuce est que vous devez éliminer les choix qui ne sont pas possibles. Pour cela, vous prenez l'aide de la règle fondamentale qui dit que si deux faces sont opposées l'une à l'autre, leur apparition simultanée dans une vue du cube n'est pas possible. Cependant, dans les compétitions d'aujourd'hui, dont le temps est précieux, le concept ne fera pas l'affaire. Vous devez être capable de résoudre une question rapidement. Il existe quelques règles secondaires pour résoudre les questions.
Rule I- Appelons ce chiffre X, dont il faut trouver l'opposé. Supposons que dans une vue quelconque du cube, X apparaisse avec Y et Z. Avec un troisième chiffre (disons A), alors X sera en face de A.
Ainsi, par exemple, vous devez trouver la face opposée 2. (C'est notre X). Maintenant, 2 apparaît sur une figure avec 1 et 3. (Y et Z). Aussi 1 et 3 apparaissent ensemble dans une autre figure, avec 5. (c'est-à-dire A). Donc 2 doit être opposé à 5.
Rule II- Nous devons trouver la face opposée de «X». Supposons que dans n'importe quelle vue du cube, X apparaisse avec Y et Z. Maintenant, supposons que Y et Z n'apparaissent pas ensemble dans d'autres vues, mais qu'ils apparaissent séparément dans deux ou plusieurs vues différentes. Ensuite, la figure commune entre les deux autres vues dans lesquelles Y et Z apparaissent séparément, sera la figure opposée à X.
Rule III- Appelons le chiffre X, dont vous devez trouver l'opposé. Maintenant, supposons que X apparaisse dans deux vues et que dans ces deux vues quatre figures différentes soient vues avec X. Alors la seule figure non vue avec X dans ces deux vues doit être opposée à X.
Summary- Vous devez garder la règle fondamentale au fond de votre esprit et ensuite appliquer trois règles secondaires pour des réponses rapides. L'approche entière peut être résumée par le diagramme suivant.
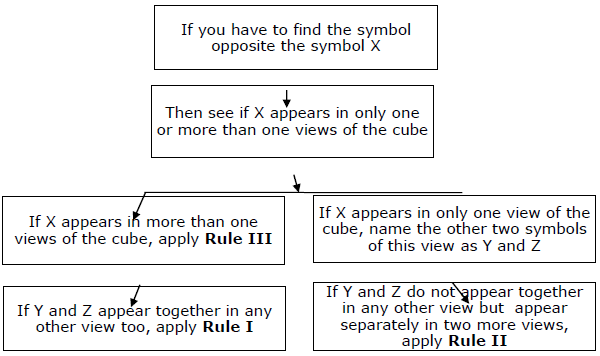
Type II
Dans ce type, nous utilisons la règle fondamentale. Cette règle nous aide à éliminer les combinaisons où les faces opposées sont affichées dans une seule vue. Cela conduira donc à l'élimination d'un choix à condition de savoir déterminer quel visage sera opposé l'un à l'autre, en regardant le "opened-up cube». À cette fin, il existe une règle très simple à l'aide de laquelle vous pouvez dire en regardant leopened-up cube, quels visages seront opposés l'un à l'autre simplement en le regardant.
La règle est donnée ci-dessous;
Third is opposite rule -
Lorsque vous voulez découvrir la face opposée d'un visage (disons X), dans la figure I, II, III; un cube ouvert est donné. Nous devons trouver quelles faces se font face lorsque le cube est fermé.
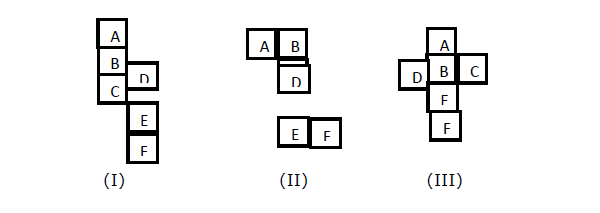
Explanation -
Dans la figure (I), le troisième chiffre de A est C. Donc A est opposé à C. Donc, D et F seront opposés. B et E seront opposés.
Dans la figure (II), B est le troisième de D, donc B sera opposé à D. De même, C sera opposé à E et A sera opposé à F.
Sur la figure (III), A est opposé à E, B est opposé à F.Donc, C est opposé à D.
Steps to solve problem
Nous pouvons maintenant résoudre des questions de ce type. On sait trouver le visage opposé en regardant unOpened-up cube. Nous savons également que dans n'importe quelle vue du cube, les faces opposées ne peuvent pas être ensemble. Par conséquent, en combinant deux règles, nous pouvons facilement résoudre des problèmes.
Sommaire
Avec cela, la discussion sur la façon de résoudre les questions de type II est terminée. Vous devez utiliser la troisième règle pour déterminer quelles faces sont opposées les unes aux autres. Le diagramme suivant donnera les informations complètes sur cette approche.

Type III
Counting of Cubes (when a varnished solid cube is cut);
Dans la section précédente, nous avons discuté du problème de trouver la face opposée d'un cube. Il y a un autre type de question liée aux cubes où un cube plus grand avec différentes couleurs vernies sur différents côtés, est divisé en plusieurs cubes plus petits et vous devez trouver le nombre de cubes ayant un seul côté verni ou deux faces vernis.
Format of this problem -
Example -
Un cube est verni avec trois couleurs vert, bleu et rouge sur ses côtés, chaque couleur étant vernie sur deux faces opposées du cube. Maintenant, le cube est divisé en 64 cubes de taille égale. Sur la base de ces informations, répondez aux questions suivantes -
1. Combien de cubes ont deux faces vernies et les faces restantes non vernies?
A - 18
B - 20
C - 22
D - 24
2. Combien de cubes ont un seul côté verni (avec une couleur verte ou bleue uniquement)
A - 4
B - 24
C - 16
D - 12
3. Combien de cubes n'ont pas de côtés vernis?
A - 0
B - 8
C - 12
D - 64