Surface d'un prisme rectangulaire constitué de cubes unitaires

Dans cette leçon, nous considérons des prismes rectangulaires constitués de cubes unitaires. On trouve la surface du prisme en comptant le nombre de faces des cubes unitaires qui composent le prisme.

Surface areadu prisme est la zone du papier qui peut être enroulée autour de la figure. Comptez le nombre de carrés ou de carrés unitaires sur les six faces. Ajoutez tous ces carrés pour obtenir la surface du prisme.

Trouvez la longueur, la largeur et la hauteur du prisme rectangulaire suivant. Trouvez ensuite sa surface.

Solution

Step 1:

Nombre de cubes unitaires sur la longueur, l = 4;

Nombre de cubes unitaires le long de la largeur, w = 3;

Nombre de cube unitaire le long de la hauteur, h = 2

Step 2:

La surface = 2 (l × w + w × h + l × h)

= 2 (4 × 3 + 4 × 2 + 2 × 3)

= 2 (12 + 8 + 6)

= 52 unités carrées

Trouvez la longueur, la largeur et la hauteur du prisme rectangulaire suivant. Trouvez ensuite sa surface.

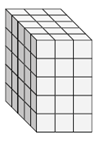
Solution

Step 1:

Nombre de cubes unitaires sur la longueur, l = 3;

Nombre de cubes unitaires le long de la largeur, w = 5;

Nombre de cube unitaire le long de la hauteur, h = 5

Step 2:

La surface = 2 (l × w + w × h + l × h)

= 2 (3 × 5 + 3 × 5 + 5 × 5)

= 2 (15 + 15 + 25)

= 110 unités carrées