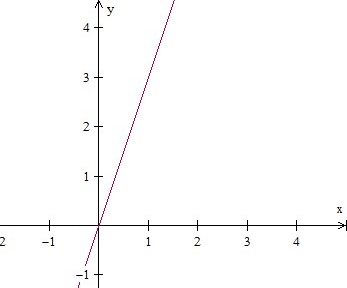
Représentation graphique d'une ligne dans le quadrant 1

introduction

On trace une ligne dont l'équation est donnée, disons par exemple y = 3x. Nous avons besoin d'au moins deux points ou paires ordonnées pour tracer la ligne. Nous choisissons d'abord des valeurs x. Ensuite, nous évaluons y = 3x pour chaque valeur de x.

Par exemple, pour x = 0, y = 3 (0) = 0; x = 1, y = 3 (1) = 3 et ainsi de suite. Nous mettons les valeurs x, y et la paire ordonnée (x, y) comme suit.

X	y	(x, y)
0	3 (0) = 0	(0,0)
1	3 (1) = 3	(1,3)
2	3 (2) = 6	(2,6)
3	3 (3) = 9	(3,9)
4	3 (4) = 12	(4,12)

On voit que les paires ordonnées se trouvent dans le quadrant 1. La jonction des points donnera le graphique de la droite dans le quadrant 1.

Exemple 1:

Tracez le graphique de la ligne dans le quadrant 1, dont l'équation est donnée ci-dessous.

2x - y = 3

Solution

Step 1:

Étant donné l'équation 2x - y = 3; pour y = 0, x = 3/2; pour x = 2, y = 2 (2) –3 = 4–3 = 1. Donc, deux paires ordonnées sont (3/2, 0) (2, 1)

Step 2:

Tracer les points et rejoindre une ligne que nous obtenons

Exemple 2:

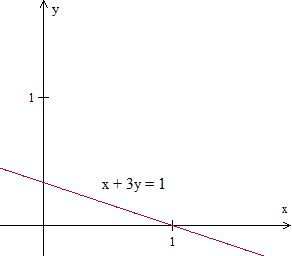
Tracez le graphique de la ligne dans le quadrant 1, dont l'équation est donnée ci-dessous.

x + 3y = 1

Solution

Step 1:

Étant donné l'équation x + 3y = 1; pour y = 0, x = 1; Pour x = 0, y = 1/3. Donc, deux paires ordonnées sont (1, 0) et (0, 1/3)

Step 2:

Tracer les points et rejoindre une ligne que nous obtenons