TensorFlow - Formation de graphiques

Une équation différentielle partielle (PDE) est une équation différentielle, qui implique des dérivées partielles avec une fonction inconnue de plusieurs variables indépendantes. En référence aux équations aux dérivées partielles, nous nous concentrerons sur la création de nouveaux graphiques.

Supposons qu'il y ait un étang de dimension 500 * 500 carré -

N = 500

Maintenant, nous allons calculer l'équation différentielle partielle et former le graphe respectif en l'utilisant. Considérez les étapes ci-dessous pour le calcul du graphe.

Step 1 - Importez des bibliothèques pour la simulation.

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

Step 2 - Inclut des fonctions pour la transformation d'un tableau 2D en un noyau de convolution et une opération de convolution 2D simplifiée.

def make_kernel(a):
   a = np.asarray(a)
   a = a.reshape(list(a.shape) + [1,1])
   return tf.constant(a, dtype=1)

def simple_conv(x, k):
   """A simplified 2D convolution operation"""
   x = tf.expand_dims(tf.expand_dims(x, 0), -1)
   y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME')
   return y[0, :, :, 0]

def laplace(x):
   """Compute the 2D laplacian of an array"""
   laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]])
   return simple_conv(x, laplace_k)
   
sess = tf.InteractiveSession()

Step 3 - Incluez le nombre d'itérations et calculez le graphique pour afficher les enregistrements en conséquence.

N = 500

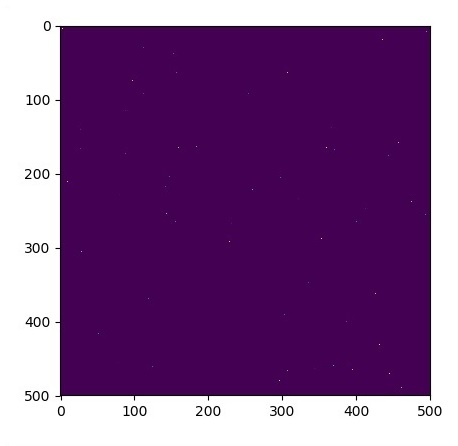
# Initial Conditions -- some rain drops hit a pond

# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)

# Some rain drops hit a pond at random points
for n in range(100):
   a,b = np.random.randint(0, N, 2)
   u_init[a,b] = np.random.uniform()

plt.imshow(u_init)
plt.show()

# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())

# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)

# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)

# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))

# Initialize state to initial conditions
tf.initialize_all_variables().run()

# Run 1000 steps of PDE
for i in range(1000):
   # Step simulation
   step.run({eps: 0.03, damping: 0.04})
   
   # Visualize every 50 steps
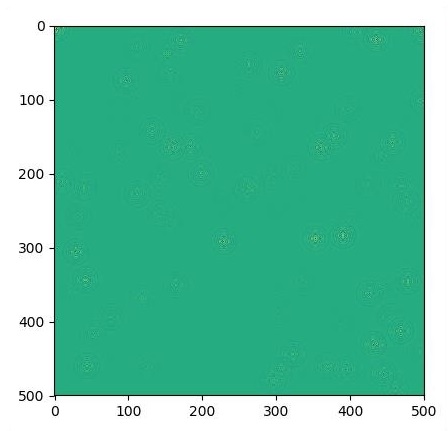
   if i % 500 == 0:
      plt.imshow(U.eval())
      plt.show()

Les graphiques sont tracés comme indiqué ci-dessous -