TensorFlow - Apprentissage de Perceptron multicouche
Le perceptron multi-couches définit l'architecture la plus compliquée des réseaux de neurones artificiels. Il est essentiellement formé de plusieurs couches de perceptron.
La représentation schématique de l'apprentissage du perceptron multicouche est illustrée ci-dessous -
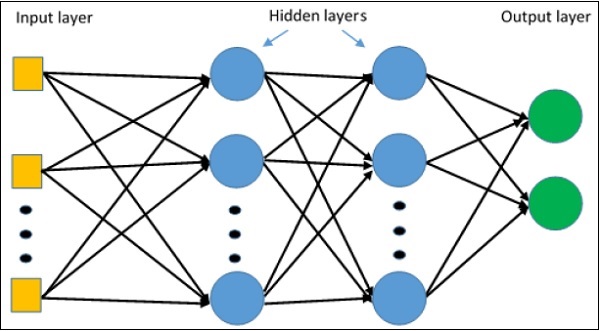
Les réseaux MLP sont généralement utilisés pour le format d'apprentissage supervisé. Un algorithme d'apprentissage typique pour les réseaux MLP est également appelé algorithme de propagation arrière.
Maintenant, nous allons nous concentrer sur l'implémentation avec MLP pour un problème de classification d'image.
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.001
training_epochs = 20
batch_size = 100
display_step = 1
# Network Parameters
n_hidden_1 = 256
# 1st layer num features
n_hidden_2 = 256 # 2nd layer num features
n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10
# MNIST total classes (0-9 digits)
# tf Graph input
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])
# weights layer 1
h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) # bias layer 1
bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1]))
# layer 1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, h), bias_layer_1))
# weights layer 2
w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2]))
# bias layer 2
bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2]))
# layer 2
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w), bias_layer_2))
# weights output layer
output = tf.Variable(tf.random_normal([n_hidden_2, n_classes]))
# biar output layer
bias_output = tf.Variable(tf.random_normal([n_classes])) # output layer
output_layer = tf.matmul(layer_2, output) + bias_output
# cost function
cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits = output_layer, labels = y))
#cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(output_layer, y))
# optimizer
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
# optimizer = tf.train.GradientDescentOptimizer(
learning_rate = learning_rate).minimize(cost)
# Plot settings
avg_set = []
epoch_set = []
# Initializing the variables
init = tf.global_variables_initializer()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples / batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss
avg_cost += sess.run(cost, feed_dict = {x: batch_xs, y: batch_ys}) / total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print
Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(avg_cost)
avg_set.append(avg_cost)
epoch_set.append(epoch + 1)
print
"Training phase finished"
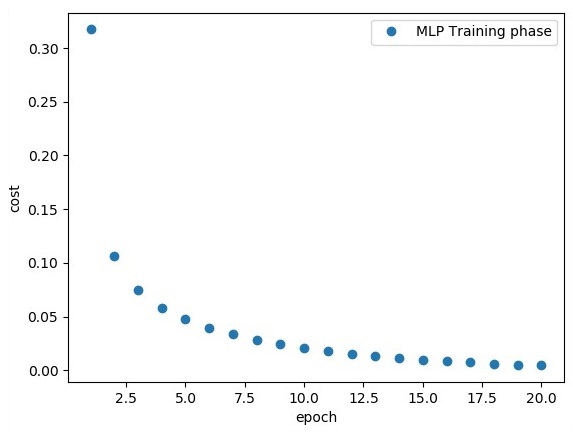
plt.plot(epoch_set, avg_set, 'o', label = 'MLP Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(output_layer, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print
"Model Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})La ligne de code ci-dessus génère la sortie suivante -