TensorFlow - Perceptron monocouche
Pour comprendre le perceptron monocouche, il est important de comprendre les réseaux de neurones artificiels (ANN). Les réseaux neuronaux artificiels sont le système de traitement de l'information dont le mécanisme s'inspire de la fonctionnalité des circuits neuronaux biologiques. Un réseau neuronal artificiel possède de nombreuses unités de traitement connectées les unes aux autres. Voici la représentation schématique du réseau neuronal artificiel -
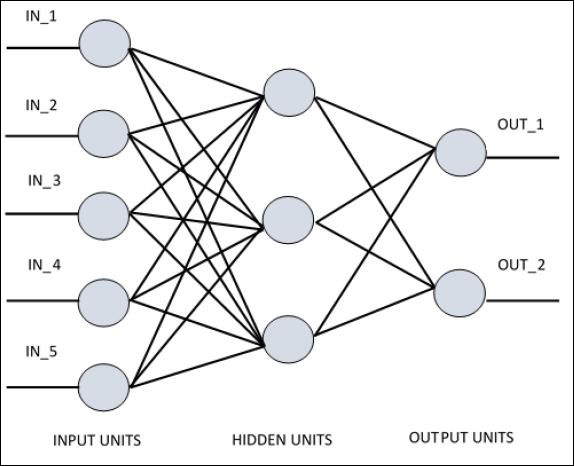
Le diagramme montre que les unités masquées communiquent avec la couche externe. Alors que les unités d'entrée et de sortie communiquent uniquement à travers la couche cachée du réseau.
Le schéma de connexion avec les nœuds, le nombre total de couches et le niveau de nœuds entre les entrées et les sorties avec le nombre de neurones par couche définissent l'architecture d'un réseau de neurones.
Il existe deux types d'architecture. Ces types se concentrent sur la fonctionnalité des réseaux de neurones artificiels comme suit -
- Perceptron monocouche
- Perceptron multicouche
Perceptron monocouche
Le perceptron monocouche est le premier modèle neuronal proposé créé. Le contenu de la mémoire locale du neurone est constitué d'un vecteur de poids. Le calcul d'un perceptron monocouche est effectué sur le calcul de la somme du vecteur d'entrée chacun avec la valeur multipliée par l'élément correspondant du vecteur des poids. La valeur affichée dans la sortie sera l'entrée d'une fonction d'activation.

Concentrons-nous sur l'implémentation du perceptron monocouche pour un problème de classification d'images utilisant TensorFlow. Le meilleur exemple pour illustrer le perceptron monocouche est la représentation de la «régression logistique».
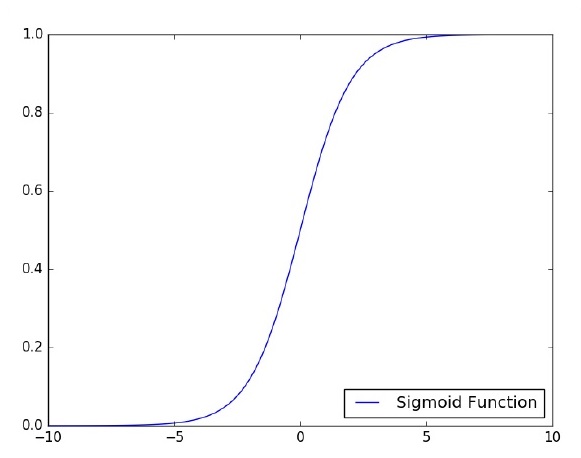
Maintenant, considérons les étapes de base suivantes de la régression logistique d'entraînement -
Les poids sont initialisés avec des valeurs aléatoires au début de la formation.
Pour chaque élément de l'ensemble d'apprentissage, l'erreur est calculée avec la différence entre la sortie souhaitée et la sortie réelle. L'erreur calculée est utilisée pour ajuster les poids.
Le processus est répété jusqu'à ce que l'erreur commise sur l'ensemble de l'apprentissage ne soit pas inférieure au seuil spécifié, jusqu'à ce que le nombre maximal d'itérations soit atteint.
Le code complet pour l'évaluation de la régression logistique est mentionné ci-dessous -
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1
# tf Graph Input
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes
# Create model
# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# Construct model
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
# Minimize error using cross entropy
cross_entropy = y*tf.log(activation)
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1))
optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost)
#Plot settings
avg_set = []
epoch_set = []
# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, \ feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
x: batch_xs, \ y: batch_ys})/total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
avg_set.append(avg_cost) epoch_set.append(epoch+1)
print ("Training phase finished")
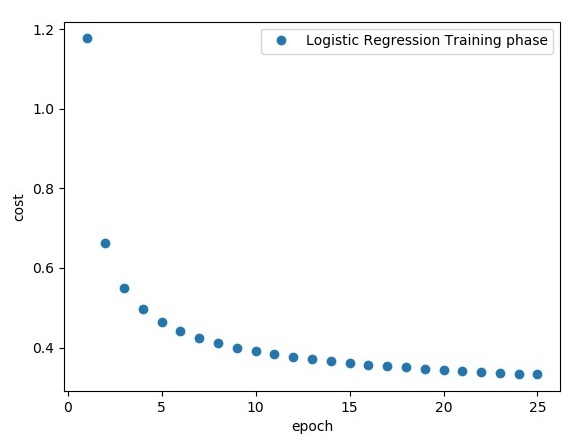
plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print
("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))Production
Le code ci-dessus génère la sortie suivante -
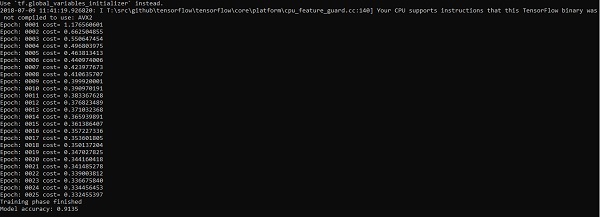
La régression logistique est considérée comme une analyse prédictive. La régression logistique est utilisée pour décrire les données et pour expliquer la relation entre une variable binaire dépendante et une ou plusieurs variables nominales ou indépendantes.