TensorFlow - Implémentation XOR

Dans ce chapitre, nous allons découvrir l'implémentation XOR à l'aide de TensorFlow. Avant de commencer avec l'implémentation XOR dans TensorFlow, voyons les valeurs de la table XOR. Cela nous aidera à comprendre le processus de cryptage et de décryptage.

UNE	B	UNE XOR B
0	0	0
0	1	1
1	0	1
1	1	0

La méthode de cryptage XOR Cipher est essentiellement utilisée pour crypter des données difficiles à craquer avec la méthode de la force brute, c'est-à-dire en générant des clés de cryptage aléatoires qui correspondent à la clé appropriée.

Le concept de mise en œuvre avec XOR Cipher consiste à définir une clé de chiffrement XOR, puis à effectuer une opération XOR sur les caractères de la chaîne spécifiée avec cette clé, qu'un utilisateur tente de chiffrer. Nous allons maintenant nous concentrer sur l'implémentation XOR à l'aide de TensorFlow, qui est mentionnée ci-dessous -

#Declaring necessary modules
import tensorflow as tf
import numpy as np
"""
A simple numpy implementation of a XOR gate to understand the backpropagation
algorithm
"""

x = tf.placeholder(tf.float64,shape = [4,2],name = "x")
#declaring a place holder for input x
y = tf.placeholder(tf.float64,shape = [4,1],name = "y")
#declaring a place holder for desired output y

m = np.shape(x)[0]#number of training examples
n = np.shape(x)[1]#number of features
hidden_s = 2 #number of nodes in the hidden layer
l_r = 1#learning rate initialization

theta1 = tf.cast(tf.Variable(tf.random_normal([3,hidden_s]),name = "theta1"),tf.float64)
theta2 = tf.cast(tf.Variable(tf.random_normal([hidden_s+1,1]),name = "theta2"),tf.float64)

#conducting forward propagation
a1 = tf.concat([np.c_[np.ones(x.shape[0])],x],1)
#the weights of the first layer are multiplied by the input of the first layer

z1 = tf.matmul(a1,theta1)
#the input of the second layer is the output of the first layer, passed through the 
   activation function and column of biases is added

a2 = tf.concat([np.c_[np.ones(x.shape[0])],tf.sigmoid(z1)],1)
#the input of the second layer is multiplied by the weights

z3 = tf.matmul(a2,theta2)
#the output is passed through the activation function to obtain the final probability

h3 = tf.sigmoid(z3)
cost_func = -tf.reduce_sum(y*tf.log(h3)+(1-y)*tf.log(1-h3),axis = 1)

#built in tensorflow optimizer that conducts gradient descent using specified 
   learning rate to obtain theta values

optimiser = tf.train.GradientDescentOptimizer(learning_rate = l_r).minimize(cost_func)

#setting required X and Y values to perform XOR operation
X = [[0,0],[0,1],[1,0],[1,1]]
Y = [[0],[1],[1],[0]]

#initializing all variables, creating a session and running a tensorflow session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

#running gradient descent for each iteration and printing the hypothesis 
   obtained using the updated theta values
for i in range(100000):
   sess.run(optimiser, feed_dict = {x:X,y:Y})#setting place holder values using feed_dict
   if i%100==0:
      print("Epoch:",i)
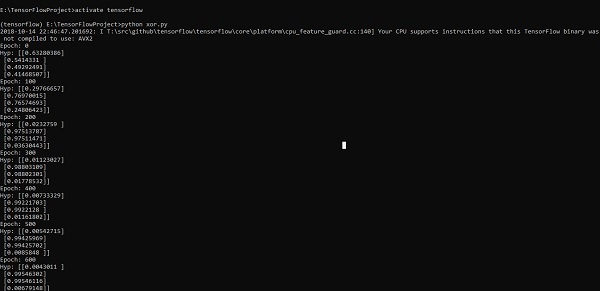
      print("Hyp:",sess.run(h3,feed_dict = {x:X,y:Y}))

La ligne de code ci-dessus génère une sortie comme indiqué dans la capture d'écran ci-dessous -