एनालॉग संचार - कोण मॉडुलन
निरंतर-तरंग मॉड्यूलेशन में अन्य प्रकार का मॉड्यूलेशन है Angle Modulation। एंगल मॉड्यूलेशन वह प्रक्रिया है जिसमें संदेश सिग्नल के अनुसार वाहक सिग्नल की आवृत्ति या चरण भिन्न होता है।
कोण संग्राहक तरंग का मानक समीकरण है
$ $ s \ बाएँ (t \ दाएँ) = A_c \ cos \ theta _i \ left (t \ दाएँ) $ $
कहाँ पे,
$ A_c $ संग्राहक तरंग का आयाम है, जो वाहक संकेत के आयाम के समान है
$ \ theta _i \ left (t \ right) $ मॉड्यूलेटेड तरंग का कोण है
कोण मॉड्यूलेशन को फ़्रीक्वेंसी मॉड्यूलेशन और फ़ेज़ मॉड्यूलेशन में विभाजित किया गया है।
Frequency Modulation संदेश सिग्नल के साथ वाहक सिग्नल की आवृत्ति को अलग-अलग करने की प्रक्रिया है।
Phase Modulation संदेश सिग्नल के साथ वाहक सिग्नल के चरण को अलग-अलग करने की प्रक्रिया है।
अब, इन पर विस्तार से चर्चा करते हैं।
आवृति का उतार - चढ़ाव
आयाम मॉडुलन में, वाहक संकेत का आयाम भिन्न होता है। जबकि, मेंFrequency Modulation (FM)वाहक सिग्नल की आवृत्ति मॉड्यूलेट सिग्नल के तात्कालिक आयाम के अनुसार भिन्न होती है।
इसलिए, आवृत्ति मॉड्यूलेशन में, आयाम और वाहक सिग्नल का चरण स्थिर रहता है। इसे निम्नलिखित आंकड़ों को देखकर बेहतर समझा जा सकता है।


मॉड्यूलेटेड तरंग की आवृत्ति बढ़ जाती है, जब मॉड्यूलेशन या संदेश सिग्नल का आयाम बढ़ जाता है। इसी तरह, मॉड्यूलेटेड तरंग की आवृत्ति कम हो जाती है, जब मॉड्यूलेट सिग्नल का आयाम कम हो जाता है। ध्यान दें कि, संग्राहक तरंग की आवृत्ति स्थिर रहती है और यह वाहक सिग्नल की आवृत्ति के बराबर होती है, जब मॉड्यूलेटिंग सिग्नल का आयाम शून्य होता है।
गणितीय प्रतिनिधित्व
एफएम मॉडुलन में तात्कालिक आवृत्ति $ f_i $ का समीकरण है
$ $ f_i = f_c + k_fm \ left (t \ right) $ $
कहाँ पे,
$ f_c $ वाहक आवृत्ति है
$ k_t $ आवृत्ति संवेदनशीलता है
$ m \ left (t \ right) $ संदेश संकेत है
हम कोणीय आवृत्ति $ \ omega_i $ और कोण $ \ theta _i \ left (t \ ") के बीच संबंध जानते हैं
$$ \ omega_i = \ frac {d \ theta _i \ left (t \ right)} {d \ _}
$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $
$ \ Rightarrow \ थीटा _i \ बाएँ (t \ दाएँ) = 2 \ pi \ int f_i
उपर्युक्त समीकरण में स्थानापन्न, $ f_i $ मूल्य।
$$ \ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ right) \ right) dt $ $
$ \ Rightarrow \ theta _i \ बाएँ (t \ दाएँ) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ बाएँ (t \ दाएँ) dt $
स्थानापन्न, कोण प्रतिरूपित तरंग के मानक समीकरण में $ \ theta_i \ left (t \ right) $ मूल्य।
$ $ s \ बाएँ (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct + 2 \ pi k_f \ int m \ बाएँ (t \ दाएँ) dt \ दाएँ) $ $
यह है equation of FM wave।
यदि मॉड्युलेटिंग सिग्नल $ m \ बाएँ (t \ दाएँ) = A_m \ cos \ बाएँ (2 \ pi f_mt \ right) $ है, तो FM तरंग का समीकरण होगा
$ $ s \ बाएँ (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct + \ beta \ sin \ बाएँ (2 \ pi f_mt \ दाएँ) \ दाएँ) $$
कहाँ पे,
$ \ बीटा $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $
एफएम संग्राहक आवृत्ति (तात्कालिक आवृत्ति) और सामान्य वाहक आवृत्ति के बीच अंतर को कहा जाता है Frequency Deviation। इसे $ \ Delta f $ द्वारा दर्शाया गया है, जो $ k_f $ और $ A_m $ के उत्पाद के बराबर है।
एफएम में विभाजित किया जा सकता है Narrowband FM तथा Wideband FM मॉड्यूलेशन इंडेक्स $ \ बीटा $ के मूल्यों के आधार पर।
नैरोबैंड एफएम
निम्नलिखित नैरोबैंड एफएम की विशेषताएं हैं।
इस आवृत्ति मॉड्यूलेशन में वाइडबैंड एफएम की तुलना में एक छोटा बैंडविड्थ होता है।
मॉड्यूलेशन इंडेक्स $ \ बीटा $ छोटा है, अर्थात, 1 से कम।
इसके स्पेक्ट्रम में वाहक, ऊपरी साइडबैंड और निचले साइडबैंड होते हैं।
इसका उपयोग मोबाइल संचार में किया जाता है जैसे पुलिस वायरलेस, एम्बुलेंस, टैक्सी, आदि।
वाइडबैंड FM
वाइडबैंड एफएम की विशेषताएं निम्नलिखित हैं।
इस आवृत्ति मॉडुलन में अनंत बैंडविड्थ है।
मॉड्यूलेशन इंडेक्स $ \ बीटा $ बड़ा है, अर्थात, 1 से अधिक है।
इसके स्पेक्ट्रम में एक वाहक और अनंत संख्या में साइडबैंड होते हैं, जो इसके आसपास स्थित होते हैं।
इसका उपयोग मनोरंजन, प्रसारण अनुप्रयोगों जैसे एफएम रेडियो, टीवी आदि में किया जाता है।
चरण मॉड्यूलेशन
आवृत्ति मॉडुलन में, वाहक की आवृत्ति भिन्न होती है। जबकि, मेंPhase Modulation (PM)वाहक सिग्नल का चरण मॉड्यूलेट सिग्नल के तात्कालिक आयाम के अनुसार बदलता रहता है।
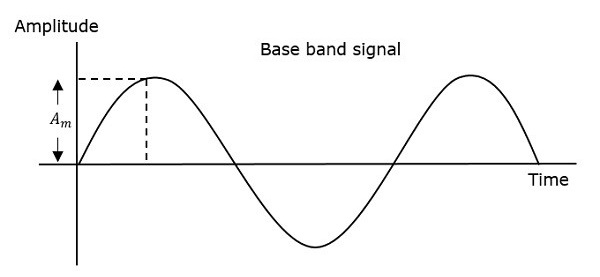
तो, चरण मॉड्यूलेशन में, आयाम और वाहक सिग्नल की आवृत्ति स्थिर रहती है। इसे निम्नलिखित आंकड़ों को देखकर बेहतर समझा जा सकता है।
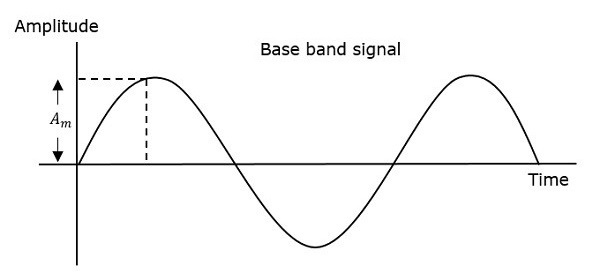

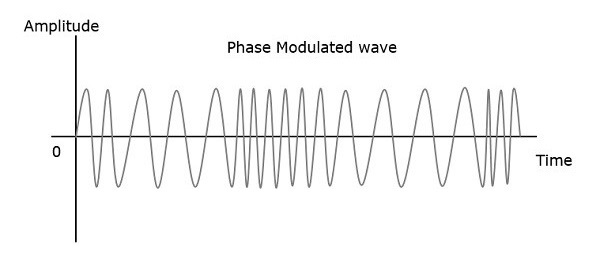
संग्राहक तरंग के चरण को अनंत बिंदु मिले हैं, जहां एक लहर में चरण परिवर्तन हो सकता है। मॉड्यूलेटिंग सिग्नल का तात्कालिक आयाम वाहक सिग्नल के चरण को बदल देता है। जब आयाम सकारात्मक होता है, तो चरण एक दिशा में बदल जाता है और यदि आयाम नकारात्मक होता है, तो चरण विपरीत दिशा में बदल जाता है।
गणितीय प्रतिनिधित्व
चरण मॉडुलन में तात्कालिक चरण $ \ phi_i $ के लिए समीकरण है
$$ \ phi _i = k_p m \ left (t \ right) $ $
कहाँ पे,
$ k_p $ चरण संवेदनशीलता है
$ m \ left (t \ right) $ संदेश संकेत है
कोण संग्राहक तरंग का मानक समीकरण है
$$ s \ बाएँ (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct + \ phi_i \ right) $$
उपर्युक्त समीकरण में स्थानापन्न, $ \ phi_i $ मूल्य।
$ $ s \ बाएँ (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct + k_p m \ बाएँ (t \ दाएँ) \ दाएँ) $$
यह है equation of PM wave।
यदि मॉड्यूलेटिंग सिग्नल, $ m \ बाएँ (t \ दाएँ) = A_m \ cos \ left (2 \ pi f_mt \ right) $ है, तो PM तरंग का समीकरण होगा
$ $ s \ बाएँ (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct + \ beta \ cos \ बाएँ (2 \ pi f_mt \ right) \ दाएँ) $$
कहाँ पे,
$ \ बीटा $ = modulation index = $ \ Delta \ phi = k_pA_m $
$ \ Delta \ phi $ चरण विचलन है
चरण संचार का उपयोग मोबाइल संचार प्रणालियों में किया जाता है, जबकि आवृत्ति मॉड्यूलेशन का उपयोग मुख्य रूप से एफएम प्रसारण के लिए किया जाता है।