एनालॉग कम्युनिकेशन - एफएम मॉड्यूलेटर
इस अध्याय में, हम उन मॉड्यूलेटर के बारे में चर्चा करते हैं जो NBFM और WBFM तरंगें उत्पन्न करते हैं। पहले, हम एनबीएफएम की पीढ़ी के बारे में चर्चा करते हैं।
एनबीएफएम की पीढ़ी
हम जानते हैं कि एफएम तरंग का मानक समीकरण है
$ $ s \ बाएँ (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct + 2 \ pi k_f \ int m \ बाएँ (t \ दाएँ) dt \ दाएँ) $ $
$ \ Rightarrow s \ left (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct \ दाएँ) \ cos \ बाएँ (2 \ pi k_f \ int m \ बाएँ (t \ दाएँ) dt का दाएँ) - $
$ A_c \ sin \ बाएँ (2 \ pi f_ct \ right) \ sin \ बाएँ (2 \ pi k_f \ int m \ बाएँ (t \ दाएँ) dt \ दाएँ) $
NBFM के लिए,
$ $ \ _ | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | <<1 $ $
हम जानते हैं कि $ \ cos \ थीटा $ 1 $ और $ \ sin \ थीटा $ 1 $ जब $ \ थीटा $ बहुत छोटा है।
उपरोक्त संबंधों का उपयोग करके, हम प्राप्त करेंगे NBFM equation जैसा
$ $ s \ बाएँ (t \ दाएँ) = A_c \ cos \ बाएँ (2 \ pi f_ct \ right) -A_c \ sin \ बाएँ (2 \ pi f_ct \ दाएँ) 2 \ pi k_f \ int \ बाएँ (t \) सही) $ $ $
एनबीएफएम मॉड्यूलेटर के ब्लॉक आरेख को निम्न आकृति में दिखाया गया है।
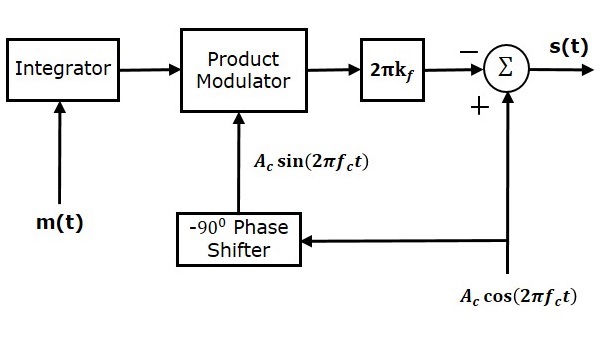
यहां, इंटीग्रेटर का उपयोग मॉड्यूलेटिंग सिग्नल $ m \ left (t \ right) $ को एकीकृत करने के लिए किया जाता है। वाहक सिग्नल $ A_c \ cos \ left (2 \ pi f_ct \ right) $ $ -90 द्वारा स्थानांतरित किया गया चरण है 0 $ $ $ A_c \ sin \ left (2 \ pi f_ct \ right) को $ $ $ $ $ $ $ -90 ^ 0 $ चरण शिफ्टर। उत्पाद मॉड्यूलेटर में दो इनपुट $ \ int m \ left (t \ दाएँ) dt $ और $ A_c \ sin \ बाएँ (2 \ pi f_ct \ right) $ हैं। यह एक आउटपुट का उत्पादन करता है, जो इन दोनों इनपुट का उत्पाद है।
यह आगे पथ में $ 2 \ pi k_f $ को अवरुद्ध करके $ 2 \ pi k_f $ के साथ गुणा किया जाता है। समर ब्लॉक में दो इनपुट होते हैं, जो एनबीएफएम समीकरण की दो शर्तों के अलावा और कुछ नहीं हैं। सकारात्मक और नकारात्मक संकेत वाहक संकेत और अन्य शब्द समर ब्लॉक के इनपुट पर दिए गए हैं। अंत में, ग्रीष्मकालीन ब्लॉक NBFM लहर का उत्पादन करता है।
डब्ल्यूबीएफएम की पीढ़ी
निम्नलिखित दो विधियाँ WBFM तरंग उत्पन्न करती हैं।
- सीधा तरीका
- अप्रत्यक्ष विधि
सीधा तरीका
इस विधि को प्रत्यक्ष विधि कहा जाता है क्योंकि हम सीधे एक विस्तृत बैंड एफएम तरंग उत्पन्न कर रहे हैं। इस विधि में WBFM को जेनरेट करने के लिए Voltage Controlled Oscillator (VCO) का उपयोग किया जाता है। VCO एक आउटपुट सिग्नल का उत्पादन करता है, जिसकी आवृत्ति इनपुट सिग्नल वोल्टेज के समानुपाती होती है। यह एफएम तरंग की परिभाषा के समान है। डब्ल्यूबीएफएम तरंग की पीढ़ी का ब्लॉक आरेख निम्नलिखित आकृति में दिखाया गया है।

यहां, वोल्ट सिग्नल कंट्रोल्ड ऑस्किलेटर (VCO) के इनपुट के रूप में मोडलिंग सिग्नल $ m \ left (t \ right) $ लगाया जाता है। VCO एक आउटपुट का उत्पादन करता है, जो WBFM के अलावा और कुछ नहीं है।
$ $ f_i \: \ Alpha \: m \ left (t \ right) $ $
$$ \ Rightarrow f_i = f_c + k_fm \ left (t \ right) $ $
कहाँ पे,
$ f_i $ WBFM तरंग की तात्कालिक आवृत्ति है।
अप्रत्यक्ष विधि
इस विधि को अप्रत्यक्ष विधि कहा जाता है क्योंकि हम अप्रत्यक्ष रूप से एक विस्तृत बैंड एफएम तरंग उत्पन्न कर रहे हैं। इसका मतलब है, पहले हम NBFM तरंग उत्पन्न करेंगे और फिर आवृत्ति गुणक की मदद से हम WBFM तरंग प्राप्त करेंगे। WBFM लहर की पीढ़ी का ब्लॉक आरेख निम्नलिखित आकृति में दिखाया गया है।

इस ब्लॉक आरेख में मुख्य रूप से दो चरण होते हैं। पहले चरण में NBFM न्यूनाधिक का उपयोग कर NBFM तरंग उत्पन्न की जाएगी। हमने इस अध्याय की शुरुआत में NBFM न्यूनाधिक के ब्लॉक आरेख को देखा है। हम जानते हैं कि NBFM तरंग का मॉड्यूलेशन इंडेक्स एक से कम है। इसलिए, एफएम तरंग की आवश्यक मॉड्यूलेशन इंडेक्स (एक से अधिक) प्राप्त करने के लिए, ठीक से आवृत्ति गुणक मूल्य चुनें।
Frequency multiplierएक गैर-रेखीय उपकरण है, जो एक आउटपुट सिग्नल का उत्पादन करता है जिसकी आवृत्ति इनपुट सिग्नल आवृत्ति का 'n' गुना है। जहां, 'n' गुणन कारक है।
यदि NBFM वेव जिसका मॉड्यूलेशन इंडेक्स $ \ बीटा $ 1 से कम है, आवृत्ति गुणक के इनपुट के रूप में लागू होता है, तो आवृत्ति गुणक एक आउटपुट सिग्नल उत्पन्न करता है, जिसका मॉड्यूलेशन इंडेक्स 'n' बार $ \ बीटा $ है और आवृत्ति भी 'n' है। 'WBFM तरंग की आवृत्ति।
कभी-कभी, हमें एफएम तरंग की आवृत्ति विचलन और मॉड्यूलेशन इंडेक्स को बढ़ाने के लिए आवृत्ति गुणक और मिक्सर के कई चरणों की आवश्यकता हो सकती है।