डेटा संरचना और एल्गोरिदम - एवीएल पेड़
क्या होगा यदि बाइनरी सर्च ट्री में इनपुट एक क्रमबद्ध (आरोही या अवरोही) तरीके से आता है? यह इस तरह दिखेगा -

यह देखा गया है कि BST का सबसे खराब प्रदर्शन रैखिक खोज एल्गोरिदम के सबसे करीब है, जो कि that (n) है। वास्तविक समय के डेटा में, हम डेटा पैटर्न और उनकी आवृत्तियों का अनुमान नहीं लगा सकते हैं। इसलिए, मौजूदा बीएसटी को संतुलित करने की आवश्यकता है।
उनके आविष्कारक के नाम पर रखा गया Adelson, Velski और Landis, AVL treesऊंचाई संतुलन बाइनरी सर्च ट्री हैं। एवीएल वृक्ष बाएं और दाएं उप-पेड़ों की ऊंचाई की जांच करता है और आश्वासन देता है कि अंतर 1 से अधिक नहीं है। इस अंतर को अंतर कहा जाता हैBalance Factor।
यहाँ हम देखते हैं कि पहला पेड़ संतुलित है और अगले दो पेड़ संतुलित नहीं हैं -
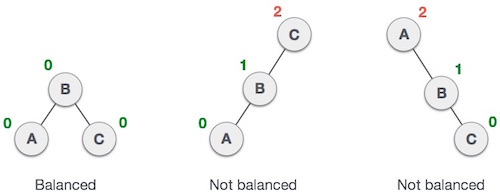
दूसरे पेड़ में, बाईं ओर के उपप्रकार C ऊँचाई 2 है और दायें सबट्री की ऊँचाई 0 है, इसलिए अंतर 2 है। तीसरे पेड़ में, दायें सबट्री का Aइसकी ऊंचाई 2 है और बाईं ओर गायब है, इसलिए यह 0 है, और अंतर फिर से 2 है। एवीएल ट्री केवल 1 होने के लिए अंतर (संतुलन कारक) की अनुमति देता है।
BalanceFactor = height(left-sutree) − height(right-sutree)यदि बाएं और दाएं उप-पेड़ों की ऊंचाई में अंतर 1 से अधिक है, तो पेड़ को कुछ रोटेशन तकनीकों का उपयोग करके संतुलित किया जाता है।
एवीएल रोटेशन
अपने आप को संतुलित करने के लिए, एक एवीएल वृक्ष निम्नलिखित चार प्रकार के चक्कर लगा सकता है -
- बायाँ घूमना
- सही रोटेशन
- बाएँ-दाएँ घूमना
- दाएं-बाएं घूमना
पहले दो घुमाव एकल घुमाव हैं और अगले दो घुमाव दोहरे घुमाव हैं। असंतुलित वृक्ष होने के लिए, हमें कम से कम ऊंचाई वाले वृक्ष की आवश्यकता होती है। 2. इस साधारण वृक्ष के साथ, आइए एक-एक करके उन्हें समझें।
वाम रोटेशन
यदि एक पेड़ असंतुलित हो जाता है, जब एक नोड को सही उपप्रकार के सही उपप्रकार में डाला जाता है, तो हम एक एकल बायां भाग बनाते हैं -

हमारे उदाहरण में, नोड Aके रूप में असंतुलित हो गया है एक नोड के सही उपशीर्षक में सही नोड में डाला जाता है। हम बाएं रोटेशन को बनाकर प्रदर्शन करते हैंA B के बाएँ उप-वर्ग
राइट रोटेशन
एवीएल पेड़ असंतुलित हो सकता है, अगर एक नोड को बाएं सबट्री के बाएं सबट्री में डाला जाता है। पेड़ को तब एक सही घुमाव की जरूरत होती है।

जैसा कि दर्शाया गया है, असंतुलित नोड दाएं घूमने से अपने बाएं बच्चे का दायां बच्चा बन जाता है।
बाएँ-दाएँ घूमना
डबल रोटेशन पहले से ही समझाया गया संस्करणों का थोड़ा जटिल संस्करण है। उन्हें बेहतर समझने के लिए, हमें रोटेशन के दौरान किए गए प्रत्येक कार्य पर ध्यान देना चाहिए। आइए पहले देखते हैं कि बाएं-दाएं रोटेशन कैसे करें। एक बाएं-दाएं रोटेशन बाएं रोटेशन का एक संयोजन है, जिसके बाद दाएं रोटेशन होता है।
| राज्य | कार्य |
|---|---|

|
एक नोड को बाएं सबट्री के दाहिने उपप्रकार में डाला गया है। यह बनाता हैCएक असंतुलित नोड। इन परिदृश्यों के कारण एवीएल पेड़ बाएं-दाएं रोटेशन का प्रदर्शन करता है। |

|
हम सबसे पहले बाईं ओर की बारीक बारीक बारी बारी से करते हैं C। यह बनाता हैAके बाएँ उपप्रकार B। |

|
नोड C अभी भी असंतुलित है, हालांकि अब, यह बाएं-उपप्रतिष्ठित के उप-वर्ग के कारण है। |

|
अब हम पेड़ को दायीं ओर घुमाएँगे B इस उपप्रकार का नया रूट नोड C अब अपने स्वयं के बाएं उपप्रकार के दाईं ओर सबट्री बन गई है। |

|
पेड़ अब संतुलित है। |
दाएं-बाएं घूमना
दूसरे प्रकार का दोहरा रोटेशन राइट-लेफ्ट रोटेशन है। यह दाएं रोटेशन का एक संयोजन है, जिसके बाद बाएं रोटेशन होता है।
| राज्य | कार्य |
|---|---|

|
एक नोड को दाईं ओर के उपप्रकार के बाएं उपप्रकार में डाला गया है। यह बनाता हैA, संतुलन कारक 2 के साथ एक असंतुलित नोड। |

|
सबसे पहले, हम साथ में सही रोटेशन करते हैं C नोड, बना रही है C अपने स्वयं के बाएँ उपशीर्षक के दाईं ओर सबट्री B। अभी,B का सही उपप्रकार बन जाता है A। |

|
नोड A अभी भी असंतुलित है क्योंकि इसके सही उपप्रकार के सही उपप्रकार और बाएं घुमाव की आवश्यकता है। |

|
एक बाएं घुमाव बनाकर प्रदर्शन किया जाता है B सबट्री की नई रूट नोड। A इसके दायें सबट्री के बाएं सबट्री बन जाता है B। |

|
पेड़ अब संतुलित है। |