संकल्पना का संकल्प
यह ट्यूटोरियल सिग्नल और सिस्टम की बहुत महत्वपूर्ण अवधारणा में से एक है। हम पूरी तरह से बातचीत पर चर्चा करेंगे। यह क्या है? क्यों यह है? हम इससे क्या हासिल कर सकते हैं?
हम छवि प्रसंस्करण की मूल बातें से दृढ़ संकल्प पर चर्चा शुरू करेंगे।
इमेज प्रोसेसिंग क्या है
जैसा कि हमने इमेज प्रोसेसिंग ट्यूटोरियल और सिग्नल और सिस्टम के परिचय में चर्चा की है कि इमेज प्रोसेसिंग सिग्नल या सिस्टम के अध्ययन को कम या ज्यादा करता है क्योंकि एक छवि एक दो आयामी सिग्नल के अलावा और कुछ नहीं है।
इसके अलावा हमने चर्चा की है कि इमेज प्रोसेसिंग में, हम एक ऐसी प्रणाली विकसित कर रहे हैं जिसका इनपुट एक छवि है और आउटपुट एक छवि होगी। यह सचित्र रूप में दर्शाया गया है।
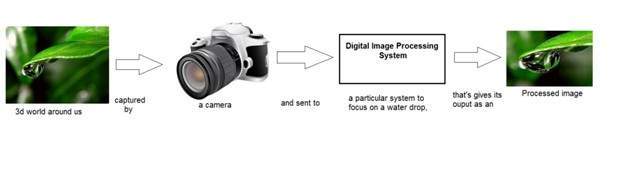
बॉक्स वह है जो "डिजिटल इमेज प्रोसेसिंग सिस्टम" के रूप में लेबल किए गए उपरोक्त आंकड़े में दिखाया गया है, जिसे ब्लैक बॉक्स के रूप में सोचा जा सकता है
इसे बेहतर रूप में प्रस्तुत किया जा सकता है:

हम अब तक कहां पहुंचे हैं
अब तक हमने छवियों में हेरफेर करने के लिए दो महत्वपूर्ण तरीकों पर चर्चा की है। या दूसरे शब्दों में हम कह सकते हैं कि, हमारा ब्लैक बॉक्स अब तक दो अलग-अलग तरीकों से काम करता है।
छवियों में हेरफेर करने के दो अलग-अलग तरीके थे
रेखांकन (हिस्टोग्राम)

इस विधि को हिस्टोग्राम प्रसंस्करण के रूप में जाना जाता है। हमने इसके विपरीत, छवि वृद्धि, चमक आदि बढ़ाने के लिए पिछले ट्यूटोरियल में विस्तार से चर्चा की है
परिवर्तन कार्य
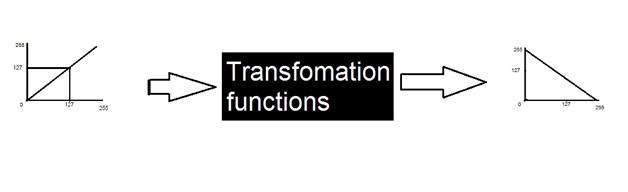
इस पद्धति को परिवर्तनों के रूप में जाना जाता है, जिसमें हमने विभिन्न प्रकार के परिवर्तनों और कुछ ग्रे स्तर के परिवर्तनों पर चर्चा की
छवियों से निपटने का दूसरा तरीका
यहां हम छवियों से निपटने के एक और तरीके पर चर्चा करने जा रहे हैं। इस अन्य विधि को दृढ़ संकल्प के रूप में जाना जाता है। आमतौर पर छवि प्रसंस्करण के लिए उपयोग किया जाने वाला ब्लैक बॉक्स (सिस्टम) एक LTI सिस्टम या रैखिक समय अक्रियाशील प्रणाली है। रैखिक से हमारा मतलब है कि ऐसी प्रणाली जहां उत्पादन हमेशा रैखिक होता है, न तो लॉग और न ही घातांक या कोई अन्य। और समय के साथ अपरिवर्तनीय का अर्थ है कि एक प्रणाली जो समय के दौरान समान रहती है।
तो अब हम इस तीसरी विधि का उपयोग करने जा रहे हैं। इसे इस रूप में दर्शाया जा सकता है।

इसे गणितीय रूप से दो तरीकों से दर्शाया जा सकता है
g(x,y) = h(x,y) * f(x,y)
इसे "मुखौटा एक छवि के साथ सजाया गया" के रूप में समझाया जा सकता है।
या
g(x,y) = f(x,y) * h(x,y)
इसे "मुखौटा के साथ चित्रित छवि" के रूप में समझाया जा सकता है।
इसे दर्शाने के दो तरीके हैं क्योंकि कनवल्शन ऑपरेटर (*) कम्यूटेटिव है। एच (एक्स, वाई) मुखौटा या फिल्टर है।
मास्क क्या है?
मास्क भी एक संकेत है। इसे दो आयामी मैट्रिक्स द्वारा दर्शाया जा सकता है। मुखौटा आमतौर पर 1x1, 3x3, 5x5, 7x7 के क्रम का होता है। एक मास्क हमेशा विषम संख्या में होना चाहिए, क्योंकि अन्य बुद्धिमान आपको मास्क के बीच में नहीं मिल सकते हैं। हमें मुखौटा के मध्य को खोजने की आवश्यकता क्यों है। इसका उत्तर नीचे दिया गया है, किस विषय में, कैसे किया जाता है?
कैसे करें कनवल्शन?
एक छवि पर दृढ़ विश्वास प्रदर्शन करने के लिए, निम्नलिखित कदम उठाए जाने चाहिए।
- केवल एक बार (क्षैतिज और लंबवत) मास्क को पलटें
- छवि पर मुखौटा स्लाइड।
- संबंधित तत्वों को गुणा करें और फिर उन्हें जोड़ें
- इस प्रक्रिया को तब तक दोहराएं जब तक कि छवि के सभी मूल्यों की गणना नहीं हो जाती।
सजा का उदाहरण
आइए कुछ दृढ़ संकल्प करते हैं। चरण 1 मास्क को फ्लिप करना है।
मुखौटा
चलो यह होने के लिए हमारा मुखौटा लें।
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
मुखौटा को क्षैतिज रूप से फ़्लिप करना
| 3 | 2 | 1 |
| 6 | 5 | 4 |
| 9 | 8 | 7 |
मुखौटा को लंबवत रूप से फ़्लिप करना
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 3 | 2 | 1 |
छवि
आइए इस तरह से एक छवि पर विचार करें
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
कनवल्शन
छवि पर मुखौटा का रूपांतरण। यह इस तरह से किया जाता है। छवि के प्रत्येक तत्व पर मास्क का केंद्र रखें। संबंधित तत्वों को गुणा करें और फिर उन्हें जोड़ें, और परिणाम को उस छवि के तत्व पर पेस्ट करें, जिस पर आप मास्क का केंद्र रखते हैं।
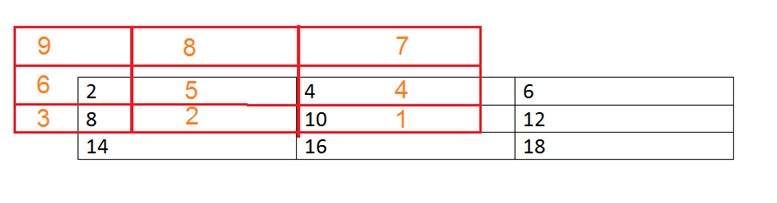
लाल रंग में बॉक्स मुखौटा है, और नारंगी में मूल्य मुखौटा के मूल्य हैं। काले रंग का बॉक्स और मान छवि के हैं। अब छवि के पहले पिक्सेल के लिए, मूल्य की गणना की जाएगी
पहला पिक्सेल = (5 * 2) + (4 * 4) + (2 * 8) + (1 * 10)
= 10 + 16 + 16 + 10
= ५२
पहली अनुक्रमणिका में मूल छवि में 52 रखें और छवि के प्रत्येक पिक्सेल के लिए इस प्रक्रिया को दोहराएं।
क्यों बातचीत
बातचीत से कुछ हासिल हो सकता है, कि छवियों को हेरफेर करने के पिछले दो तरीके हासिल नहीं कर सकते हैं। इनमें धुंधलापन, पैनापन, किनारे का पता लगाना, शोर कम करना आदि शामिल हैं