माइक्रोवेव इंजीनियरिंग - एच-प्लेन टी
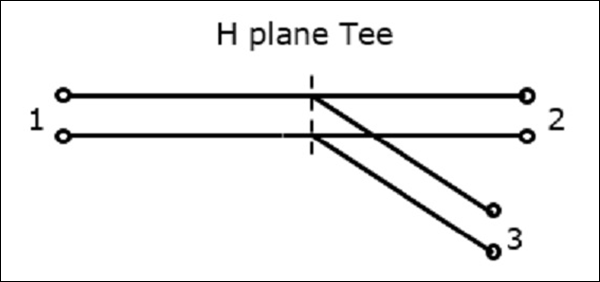
एक एच-प्लेन टी जंक्शन एक साधारण वेवगाइड को एक आयताकार वेवगाइड के साथ जोड़कर बनाया गया है जिसमें पहले से ही दो पोर्ट हैं। आयताकार वेवगाइड्स की भुजाएं दो पोर्ट बनाती हैंcollinear ports यानी, पोर्ट 1 और पोर्ट 2, जबकि नए वाले, पोर्ट 3 को साइड आर्म या कहा जाता है H-arm। इस एच-प्लेन टी को भी कहा जाता हैShunt Tee।
चूंकि साइड आर्म की धुरी चुंबकीय क्षेत्र के समानांतर होती है, इसलिए इस जंक्शन को एच-प्लेन टी जंक्शन कहा जाता है। इसे भी कहा जाता हैCurrent junction, क्योंकि चुंबकीय क्षेत्र खुद को हथियारों में विभाजित करता है। एच-प्लेन टी के क्रॉस-सेक्शनल विवरण को निम्न आकृति द्वारा समझा जा सकता है।

निम्नलिखित आंकड़ा धारावाहिक के रूप में द्वि-दिशात्मक तरंग द्वारा धारावाहिक बंदरगाह बनाने के लिए कनेक्शन को दर्शाता है।
एच-प्लेन टी के गुण
एच-प्लेन टी के गुणों को इसके $ \ _ [S \ right] _ {3 \ 3 3} $ मैट्रिक्स द्वारा परिभाषित किया जा सकता है।
यह एक 3 × 3 मैट्रिक्स है क्योंकि 3 संभावित इनपुट और 3 संभावित आउटपुट हैं।
$ [S] = \ start {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} और S_ {22} & S_ {23} \\ S_ {31} और #_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
बिखरे हुए गुणांक $ S_ {13} $ और $ S_ {23} $ यहां बराबर हैं क्योंकि जंक्शन सममित रूप से समतल है।
सममित संपत्ति से,
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} = S_ {13} \: \: S_ {13} = S_ {31} $
पोर्ट पूरी तरह से मेल खाता है
$ S_ {33} = 0 $
अब, $ [एस] $ मैट्रिक्स के रूप में लिखा जा सकता है,
$ [S] = \ start {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} और #_ {13 } & 0 \ end {bmatrix} $ ........ Equation 2
हम कह सकते हैं कि समरूपता संपत्ति को देखते हुए हमारे पास चार अज्ञात हैं।
एकात्मक संपत्ति से
$$ [S] [S] \ ast = [I] $ $
$$ \ start {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ [13] और 0 \ end {bmatrix} \: \ start {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} और S_ {13} ^ {*} \\ S_ {12} ^ {*} और S_ {22} ^ {*} & S_ {13} ^ {*} \\ S_ {13} ^ {*} & S_ {13} ^ {*} & 0 \ end {bmatrix} = \ _ {bmatrix} 1 और 0 & 0 \\ 0 & 1 और 0 \\ 0 & 0 & 1 \ अंत {bmatrix} $ $
हम प्राप्त गुणा,
(पंक्ति के रूप में नोटिंग R और कॉलम के रूप में C)
$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ _ बाएं | S_ {11} \ सही | ^ 2 + \ बाएँ | S_ {12} \ दाएँ | ^ 2 + \ बाएँ | S_ {13} \ right | ^ 2 = 1 $........ Equation 3
$ R_2C_2: \ left | S_ {12} \ दाएँ | ^ 2 + \ बाएँ | S_ {22} \ सही | ^ 2 + \ बाएँ | S_ {13} \ right | ^ 2 = 1 $......... Equation 4
$ R_3C_3: \ left | S_ {13} \ सही | ^ 2 + \ बाएँ | S_ {13} \ right | ^ 2 = 1 $......... Equation 5
$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 0 $ ......... Equation 6
$ 2 \ बाईं | S_ {13} \ right | ^ 2 = 1 \ quad या \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 7
$ \ _ बाएं | S_ {11} \ सही | ^ 2 = \ बाएँ | S_ {22} \ right | ^ 2 $
$ S_ {11} = S_ {22} $ ......... Equation 8
समीकरण 6 से, $ S_ {13} \ left (S_ {11} ^ {*} + S_ {12} ^ {*} \ right) = 0 $
चूँकि, $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: या \ _: S_ {11} ^ {*} -S_ {12} ^ {} $ *
या $ S_ {11} = -S_ {12} \: \: या \: \: S_ {12} = -S_ {11} $......... Equation 9
समीकरण 3 में इनका उपयोग करना,
चूँकि, $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: या \ _: S_ {11} ^ {*} -S_ {12} ^ {} $ *
$ \ _ बाएं | S_ {11} \ सही | ^ 2 + \ बाएँ | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 \ quad या \ quad 2 \ बाएँ | S_ {11} \ right | ^ 2 = \ frac {1} {2} \ quad या \ quad S_ {11} = \ frac {1} {2} $..... Equation 10
समीकरण 8 और 9 से,
$ S_ {12} = - \ frac {1} {2} $......... Equation 11
$ S_ {22} = \ frac {1} {2} $......... Equation 12
$ S_ {13} $, $ S_ {11} $, $ S_ {12} $ और $ S_ {22} $ समीकरण 7 और 10, 11 और 12 से समीकरण 2 में प्रतिस्थापित करना।
हमें मिला,
$ $ \ छोड़ दिया [S \ right] = \ start {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
हम जानते हैं कि $ [b] $ = $ [s] [a] $ है
$$ \ start {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ start {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & frac {1} { \ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt { 2}} & \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ start {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
यह एच-प्लेन टी के लिए बिखरने वाला मैट्रिक्स है, जो इसके बिखरने के गुणों की व्याख्या करता है।