माइक्रोवेव इंजीनियरिंग - माइक्रोवेव डिवाइस
अन्य प्रणालियों की तरह, माइक्रोवेव सिस्टम में कई माइक्रोवेव घटक होते हैं, मुख्य रूप से एक छोर पर स्रोत और दूसरे पर लोड होता है, जो सभी वेवगाइड्स या समाक्षीय केबल या ट्रांसमिशन लाइन सिस्टम से जुड़े होते हैं।
निम्नलिखित waveguides के गुण हैं।
- उच्च एस.एन.आर.
- कम क्षीणन
- कम प्रविष्टि नुकसान
वेवगाइड माइक्रोवेव फ़ंक्शंस
4 बंदरगाहों वाले एक वेवगाइड पर विचार करें। यदि बिजली एक बंदरगाह पर लागू होती है, तो यह कुछ अनुपातों में सभी 3 बंदरगाहों से गुजरती है, जहां कुछ इसे उसी बंदरगाह से वापस प्रतिबिंबित कर सकते हैं। इस अवधारणा को निम्नलिखित आकृति में स्पष्ट रूप से दर्शाया गया है।
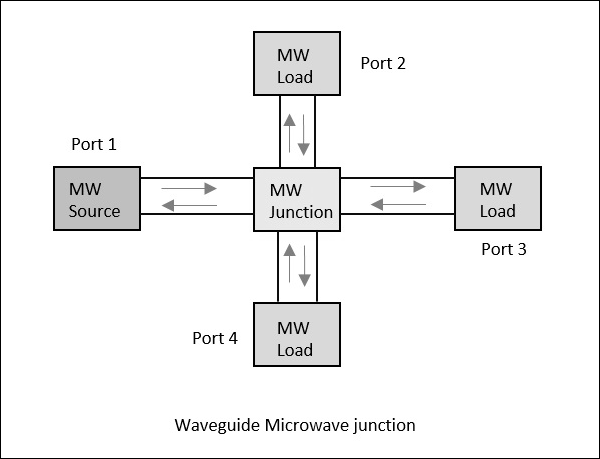
स्कैटरिंग पैरामीटर्स
दो-पोर्ट नेटवर्क के लिए, जैसा कि निम्नलिखित आंकड़े में दिखाया गया है, यदि बिजली एक बंदरगाह पर लागू होती है, जैसा कि हमने अभी चर्चा की है, अधिकांश शक्ति दूसरे बंदरगाह से बच जाती है, जबकि इसमें से कुछ उसी बंदरगाह पर वापस प्रतिबिंबित होती है। निम्नलिखित आकृति में, यदिV1 या V2 तब लागू किया जाता है I1 या I2 क्रमशः प्रवाह।
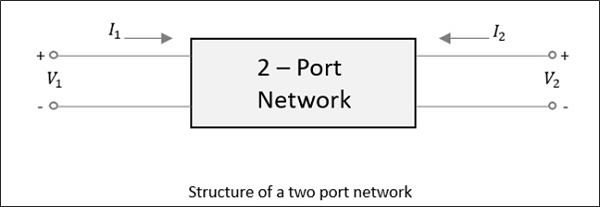
यदि स्रोत को विपरीत पोर्ट पर लागू किया जाता है, तो एक और दो संयोजनों पर विचार किया जाना है। तो, दो-पोर्ट नेटवर्क के लिए, 2 × 2 = 4 संयोजन होने की संभावना है।
संबंधित शक्तियों के साथ यात्रा तरंगें जब बंदरगाहों के माध्यम से बिखर जाती हैं, तो माइक्रोवेव जंक्शन को एस-पैरामीटर्स या द्वारा परिभाषित किया जा सकता है Scattering Parameters, जिसे मैट्रिक्स रूप में दर्शाया जाता है, जिसे "कहा जाता है"Scattering Matrix"।
बिखरे हुए मैट्रिक्स
यह एक वर्ग मैट्रिक्स है जो माइक्रोवेव जंक्शन के विभिन्न इनपुट और आउटपुट पोर्ट के बीच बिजली संबंधों के सभी संयोजन देता है। इस मैट्रिक्स के तत्वों को कहा जाता है"Scattering Coefficients" या "Scattering (S) Parameters"।
निम्नलिखित आकृति पर विचार करें।

यहाँ, स्रोत $ i ^ {th} $ लाइन से जुड़ा है जबकि $ a_1 $ घटना तरंग है और $ b_1 $ प्रतिबिंबित लहर है।
यदि कोई रिश्ता $ b_1 $ और $ a_1 $ के बीच दिया जाता है,
$ $ b_1 = (प्रतिबिंब \: \: गुणांक) a_1 = S_ {1i} a_1 $ $
कहाँ पे
$ S_ {1i} $ = $ 1 का परावर्तन गुणांक ^ {st} $ लाइन (जहां $ i $ इनपुट पोर्ट है और $ 1 $ आउटपुट पोर्ट है)
$ 1 $ = $ 1 ^ {सेंट} $ लाइन से प्रतिबिंब
$ i $ = स्रोत $ i ^ {th} $ लाइन पर जुड़ा हुआ है
यदि प्रतिबाधा मेल खाती है, तो बिजली लोड में स्थानांतरित हो जाती है। पूरी तरह से, अगर लोड प्रतिबाधा विशेषता प्रतिबाधा के साथ मेल नहीं खाती है। तब, प्रतिबिंब होता है। इसका मतलब है, अगर प्रतिबिंब होता है
$ $ Z_l \ neq Z_o $$
हालांकि, अगर यह बेमेल एक से अधिक पोर्ट के लिए है, उदाहरण के लिए $ 'n' $ पोर्ट, तो $ i = 1 $ से $ n $ (चूंकि $ i $ $ $ 1 से $ n $ तक कोई भी रेखा हो सकती है)।
इसलिए, हमारे पास है
$ $ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$
$ $ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$
$$। $$
$$। $$
$$। $$
$$। $$
$$। $$
$ $ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$
जब यह पूरी चीज मैट्रिक्स रूप में रखी जाती है,
$ $ \ _ {bmatrix} b_1 \\ b_2 \\ b_3 \\। \\। \\। \\। \\ b_n \ end {bmatrix} = \ start {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\। & ... & ... & ...। \\। &। & ... & ...। \\। &। & ... & ...। \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ टाइम्स \ bmatrix} a_1 \\ a_2 \ a_3 \\। \ _ शुरू करें। \ _। \\। \\ a_n \ end {bmatrix} $$
Column matrix $ [ख] $ Scattering matrix $ [एस] $Matrix $ [एक] $
कॉलम मैट्रिक्स $ \ छोड़ दिया [b \ right] $ प्रतिबिंबित तरंगों या आउटपुट से मेल खाता है, जबकि मैट्रिक्स $ \ left [a \ right] $ घटना तरंगों या इनपुट से मेल खाती है। प्रकीर्णन कॉलम मैट्रिक्स $ \ left [s \ right] $ जो $ n \ n n $ के क्रम का है, जिसमें प्रतिबिंब गुणांक और ट्रांसमिशन गुणांक होते हैं। इसलिए,
$ $ \ _ [b \ दाएँ] = \ बाएँ [S \ दाएँ] \ बाएँ [a \ दाएँ] $ $
[एस] मैट्रिक्स के गुण
बिखरने वाली मैट्रिक्स को $ [S] $ मैट्रिक्स के रूप में दर्शाया गया है। $ [S] $ मैट्रिक्स के लिए कुछ मानक गुण हैं। वे हैं -
-
$ [S] $ हमेशा ऑर्डर का एक वर्ग मैट्रिक्स होता है (nxn)
$ [S] _ {n \ टाइम्स n} $
-
$ [S] $ एक सममित मैट्रिक्स है
यानी, $ S_ {ij} = S_ {ji} $
-
$ [S] $ एक एकात्मक मैट्रिक्स है
यानी, $ [S] [S] ^ * = I $
किसी पंक्ति या स्तंभ के प्रत्येक शब्द के उत्पादों का योग किसी अन्य पंक्ति या स्तंभ के संबंधित शब्दों के जटिल संयुग्म द्वारा गुणा किया जाता है। अर्थात,
$$ \ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \: for \: k \ neq j $$
$ $ (k = 1,2,3, ... \: n) \: और \: (j = 1,2,3, ... \:) "%"
-
यदि कुछ $ k ^ {th} $ बंदरगाह और जंक्शन के बीच विद्युत दूरी $ \ बीटा _kI_k $ है, तो $ S_ {ij} $ $ k $ के गुणांक, कारक $ e ^ {से गुणा किया जाएगा। j \ Beta kIk} $
अगले कुछ अध्यायों में, हम विभिन्न प्रकार के माइक्रोवेव टी जंक्शनों पर एक नज़र डालेंगे।