माइक्रोवेव इंजीनियरिंग - ट्रांसमिशन लाइन्स
ए transmission lineएक कनेक्टर है जो ऊर्जा को एक बिंदु से दूसरे तक पहुंचाता है। ट्रांसमिशन लाइन सिद्धांत का अध्ययन शक्ति और उपकरणों के प्रभावी उपयोग में सहायक है।
मूल रूप से चार प्रकार की संचरण लाइनें हैं -
- दो-तार समानांतर ट्रांसमिशन लाइनें
- समाक्षीय रेखाएँ
- पट्टी प्रकार सब्सट्रेट ट्रांसमिशन लाइनों
- Waveguides
संचारित करते समय या प्राप्त करते समय, ऊर्जा के हस्तांतरण को प्रभावी ढंग से किया जाना चाहिए, शक्ति के अपव्यय के बिना। इसे प्राप्त करने के लिए, कुछ महत्वपूर्ण पैरामीटर हैं जिन पर विचार किया जाना है।
ट्रांसमिशन लाइन के मुख्य पैरामीटर
एक ट्रांसमिशन लाइन के महत्वपूर्ण पैरामीटर प्रतिरोध, प्रेरण, समाई और चालन हैं।
प्रतिरोध और अधिष्ठापन को एक साथ ट्रांसमिशन लाइन कहा जाता है impedance।
समाई और चालकता को एक साथ कहा जाता है admittance।
प्रतिरोध
सामग्री द्वारा प्रस्तुत प्रतिरोध, जिसमें से ट्रांसमिशन लाइनें बनाई जाती हैं, विशेष रूप से छोटी लाइनों के लिए, काफी मात्रा में होगी। जैसे ही लाइन करंट बढ़ता है, ओमिक लॉस $ \ लेफ्ट (I ^ {2} R \: loss \ right) $ भी बढ़ जाता है।
प्रतिरोध $R$ लंबाई का एक चालक "$l$" और क्रॉस-सेक्शन "$a$" के रूप में प्रतिनिधित्व किया है
$ $ R = \ rho \ frac {l} {a} $ $
कहाँ पे
Ѓ $ \ rho $ = कंडक्टर सामग्री की प्रतिरोधकता, जो निरंतर है।
तापमान और धारा की आवृत्ति मुख्य कारक हैं जो एक पंक्ति के प्रतिरोध को प्रभावित करते हैं। एक कंडक्टर का प्रतिरोध तापमान में परिवर्तन के साथ रैखिक रूप से भिन्न होता है। जबकि, यदि वर्तमान की आवृत्ति बढ़ती है, तो कंडक्टर की सतह के प्रति वर्तमान घनत्व भी बढ़ जाता है। अन्यथा, कंडक्टर के केंद्र की ओर वर्तमान घनत्व बढ़ जाता है।
इसका मतलब है, कंडक्टर की सतह की ओर अधिक धारा प्रवाहित होती है, यह केंद्र की ओर कम बहती है, जिसे इस रूप में जाना जाता है Skin Effect।
अधिष्ठापन
एक एसी ट्रांसमिशन लाइन में, प्रवाह साइनसोइड रूप से प्रवाहित होता है। यह करंट विद्युत क्षेत्र के लिए एक चुंबकीय क्षेत्र को प्रेरित करता है, जो साइनसॉइड रूप से भी भिन्न होता है। इसे फैराडे के कानून के रूप में जाना जाता है। फ़ील्ड को निम्न आकृति में दर्शाया गया है।

यह अलग-अलग चुंबकीय क्षेत्र कंडक्टर में कुछ ईएमएफ को प्रेरित करता है। अब यह प्रेरित वोल्टेज या ईएमएफ विपरीत दिशा में शुरू में बहने वाली दिशा में बहता है। विपरीत दिशा में बहने वाली यह ईएमएफ समकक्ष है जिसे एक पैरामीटर के रूप में जाना जाता हैInductance, जो वर्तमान में बदलाव का विरोध करने की संपत्ति है।
इसे "L"माप की इकाई है"Henry(H)"।
प्रवाहकत्त्व
ट्रांसमिशन लाइन और ग्राउंड के बीच लीकेज करंट होगा, और फेज कंडक्टरों के बीच भी। लीकेज करंट की यह छोटी मात्रा आमतौर पर इन्सुलेटर की सतह से बहती है। इस लीकेज करंट का उलटा ही कहा जाता हैConductance। इसे "G"।
लाइन करंट का प्रवाह अधिष्ठापन से जुड़ा होता है और दो बिंदुओं के बीच वोल्टेज का अंतर समाई से जुड़ा होता है। प्रेरण चुंबकीय क्षेत्र से जुड़ा होता है, जबकि धारिता विद्युत क्षेत्र से जुड़ा होता है।
समाई
के बीच वोल्टेज अंतर Phase conductorsकंडक्टरों के बीच एक विद्युत क्षेत्र को जन्म देता है। दो कंडक्टर समानांतर प्लेटों की तरह हैं और उनके बीच की हवा ढांकता हुआ बन जाती है। यह पैटर्न कंडक्टरों के बीच समाई प्रभाव को जन्म देता है।
विशेषता प्रतिबाधा
यदि एक समान दोषरहित संचरण रेखा मानी जाती है, तो एक दिशा में यात्रा करने वाली तरंग के लिए, उस रेखा के साथ वोल्टेज और करंट के आयामों का अनुपात, जिसमें कोई प्रतिबिंब नहीं होता है, इसे कहा जाता है Characteristic impedance।
इसे $ Z_0 $ द्वारा निरूपित किया जाता है
$$ Z_0 = \ sqrt {\ frac {वोल्टेज \: \: तरंग \: \: मान} {वर्तमान \: \: लहर \: \: मूल्य}} $ $
$ $ Z_0 = \ sqrt {\ frac {R + jwL} {G + jwC}} $ $
दोषरहित रेखा के लिए, $ R_0 = \ sqrt {\ frac {L} {C}} $
जहां $ L $ और $ C $ प्रति यूनिट लंबाई के लिए अधिष्ठापन और समाई हैं।
प्रतिबाधा मिलान
लोड को अधिकतम बिजली हस्तांतरण प्राप्त करने के लिए, प्रतिबाधा मिलान करना होगा। इस प्रतिबाधा मिलान को प्राप्त करने के लिए, निम्नलिखित शर्तों को पूरा करना है।
लोड का प्रतिरोध स्रोत के बराबर होना चाहिए।
$ $ R_L = R_S $ $
लोड की प्रतिक्रिया स्रोत के बराबर होनी चाहिए लेकिन साइन में विपरीत।
$ $ X_L = -X_S $ $
जिसका अर्थ है, यदि स्रोत आगमनात्मक है, तो लोड कैपेसिटिव होना चाहिए और इसके विपरीत।
परावर्तन सह-कुशल
ट्रांसमिशन लाइन में प्रतिबाधा बेमेल के कारण परिलक्षित ऊर्जा की मात्रा को व्यक्त करने वाले पैरामीटर को कहा जाता है Reflection coefficient। यह $ \ rho $ द्वारा इंगित किया गया है(rho)।
इसे "लोड टर्मिनलों पर घटना वोल्टेज में प्रतिबिंबित वोल्टेज के अनुपात" के रूप में परिभाषित किया जा सकता है।
$ $ \ rho = \ frac {प्रतिबिंबित \: वोल्टेज} {घटना \: वोल्टेज} = \ frac {V_r} {V_i} \: at \: लोड \: टर्मिनल $ $
यदि डिवाइस और ट्रांसमिशन लाइन के बीच की बाधा एक दूसरे से मेल नहीं खाती है, तो ऊर्जा परिलक्षित होती है। उच्च ऊर्जा परिलक्षित होती है, अधिक से अधिक $ \ rho $ प्रतिबिंब गुणांक का मूल्य होगा।
वोल्टेज स्टैंडिंग वेव अनुपात (VSWR)
खड़ी लहर तब बनती है जब घटना की लहर परिलक्षित होती है। खड़ी लहर जो बनती है, उसमें कुछ वोल्टेज होता है। खड़े तरंगों की परिमाण को तरंग तरंग अनुपात के संदर्भ में मापा जा सकता है।
एक खड़े लहर में न्यूनतम वोल्टेज के लिए अधिकतम वोल्टेज के अनुपात को वोल्टेज स्टैंडिंग वेव अनुपात (वीएसडब्ल्यूआर) के रूप में परिभाषित किया जा सकता है। इसे "$ S $" द्वारा दर्शाया गया है।
$ $ S = \ frac {\ left | V_ {max} \ right |} {\ left | V_ {{}} \ right |} \ quad 1 \: \ leq S \ leq \ infty $$
वीएसडब्ल्यूआर वोल्टेज स्टेंडिंग वेव पैटर्न का वर्णन करता है जो चरण जोड़ और घटना और प्रतिबिंबित तरंगों के घटाव के कारण ट्रांसमिशन लाइन में मौजूद है।
इसलिए, यह भी लिखा जा सकता है
$ $ S = \ frac {1 + \ rho} {1 - \ rho} $ $
प्रतिबाधा जितनी बड़ी बेमेल होगी, उतनी ही उंची लहर का आयाम होगा। इसलिए, यदि प्रतिबाधा पूरी तरह से मेल खाती है,
$ $ V_ {अधिकतम}: V_ {मिनट} = 1: 1 $ $
इसलिए, वीएसडब्ल्यूआर के लिए मूल्य एकता है, जिसका अर्थ है कि संचरण एकदम सही है।
ट्रांसमिशन लाइन्स की क्षमता
ट्रांसमिशन लाइनों की दक्षता को आउटपुट पावर के इनपुट पावर के अनुपात के रूप में परिभाषित किया गया है।
$ \% \: दक्षता \: की: \: ट्रांसमिशन \: लाइन \: \ eta = \ frac {पावर \: दिया \: at \: रिसेप्शन} {पावर \: भेजा \: from \: the \: ट्रांसमिशन \: अंत} \ 100 बार $
वोल्टेज अधिनियम
वोल्टेज विनियमन को ट्रांसमिशन लाइन के भेजने और प्राप्त करने वाले छोरों के बीच वोल्टेज के परिमाण में परिवर्तन के रूप में परिभाषित किया गया है।
$ \% \: वोल्टेज \: नियमन = \ frac {भेजने वाला: अंत \: वोल्टेज - \: प्राप्त करना: \: अंत \: वोल्टेज} {भेजना: अंत \: वोल्टेज} \ 100 बार $
प्रतिबाधा बेमेल के कारण नुकसान
ट्रांसमिशन लाइन, यदि एक मिलान लोड के साथ समाप्त नहीं हुई है, तो नुकसान में होती है। ये नुकसान कई प्रकार के होते हैं जैसे क्षीणन हानि, परावर्तन हानि, संचरण हानि, वापसी हानि, सम्मिलन हानि, आदि।
क्षीणन हानि
ट्रांसमिशन लाइन में सिग्नल के अवशोषण के कारण होने वाली हानि को एटनरेशन लॉस कहा जाता है, जिसे प्रतिनिधित्व किया जाता है
$ $ Attenuation \: नुकसान (dB) = 10 \: log_ {10} \ left [\ frac {E_i - E_r} {E_t} \ right] $$
कहाँ पे
$ E_i $ = इनपुट ऊर्जा
$ E_r $ = भार से इनपुट तक परिलक्षित ऊर्जा
$ E_t $ = भार को प्रेषित ऊर्जा
परावर्तन हानि
ट्रांसमिशन लाइन के प्रतिबाधा बेमेल के कारण सिग्नल के प्रतिबिंब के कारण होने वाली हानि को परावर्तन हानि के रूप में कहा जाता है, जिसे इस रूप में दर्शाया गया है
$ $ परावर्तन \: नुकसान (dB) = 10 \: log_ {10} \ left [\ frac {E_i} {E_i - E_r} \ right] $$
कहाँ पे
$ E_i $ = इनपुट ऊर्जा
$ E_r $ = भार से परिलक्षित ऊर्जा
ट्रांसमिशन हानि
ट्रांसमिशन लाइन के माध्यम से संचरण करते समय होने वाली हानि को ट्रांसमिशन हानि के रूप में कहा जाता है, जिसे इस रूप में दर्शाया गया है
$ $ ट्रांसमिशन \: नुकसान (डीबी) = 10 \: लॉग_ {10} \: \ frac {E_i} {E_t} $ $
कहाँ पे
$ E_i $ = इनपुट ऊर्जा
$ E_t $ = संचरित ऊर्जा
हारकर लौटा
ट्रांसमिशन लाइन द्वारा परिलक्षित शक्ति की माप को रिटर्न लॉस कहा जाता है, जिसे इस रूप में दर्शाया गया है
$ $ रिटर्न \: नुकसान (डीबी) = 10 \: लॉग_ {10} \: \ frac {E_i} {E_r} $ $
कहाँ पे
$ E_i $ = इनपुट ऊर्जा
$ E_r $ = परिलक्षित ऊर्जा
निविष्टी की हानि
ट्रांसमिशन लाइन के बिना ऊर्जा हस्तांतरण की तुलना में ट्रांसमिशन लाइन का उपयोग करके ऊर्जा हस्तांतरण के कारण होने वाली हानि को सम्मिलन हानि के रूप में कहा जाता है, जिसे निम्न के रूप में प्रस्तुत किया जाता है।
$ $ प्रविष्टि \: नुकसान (डीबी) = 10 \: लॉग_ {10} \: \ frac {E_1} {E_2} $ $
कहाँ पे
$ E_1 $ = लोड द्वारा प्राप्त ऊर्जा जब सीधे ट्रांसमिशन लाइन के बिना स्रोत से जुड़ी होती है।
$ E_2 $ = लोड द्वारा प्राप्त ऊर्जा जब ट्रांसमिशन लाइन लोड और स्रोत के बीच जुड़ी होती है।
ठूंठ मिलान
यदि लोड प्रतिबाधा स्रोत प्रतिबाधा को बेमेल कर देती है, तो "स्टब मैचिंग" नामक एक विधि का उपयोग कभी-कभी मिलान प्राप्त करने के लिए किया जाता है।
खुले या शॉर्ट सर्किट लाइनों के वर्गों को जोड़ने की प्रक्रिया कहा जाता है stubs कुछ बिंदु या बिंदुओं पर मुख्य लाइन के साथ शंट, के रूप में कहा जा सकता है Stub Matching।
उच्चतर माइक्रोवेव आवृत्तियों पर, मूल रूप से दो स्टब मिलान तकनीक कार्यरत हैं।
एकल ठूंठ मिलान
सिंगल स्टब मैचिंग में, निश्चित निश्चित लंबाई के एक स्टब को लोड से कुछ दूरी पर रखा जाता है। इसका उपयोग केवल एक निश्चित आवृत्ति के लिए किया जाता है, क्योंकि आवृत्ति में किसी भी परिवर्तन के लिए, स्टब का स्थान बदलना पड़ता है, जो नहीं किया जाता है। यह विधि समाक्षीय लाइनों के लिए उपयुक्त नहीं है।
डबल स्टब मिलान
डबल स्टड मिलान में, कुछ स्थितियों पर चर लंबाई के दो स्टब्स तय किए जाते हैं। जैसे ही भार बदलता है, मिलान प्राप्त करने के लिए केवल स्टब्स की लंबाई समायोजित की जाती है। यह एक एकल आवृत्ति मिलान उपकरण के रूप में प्रयोगशाला अभ्यास में व्यापक रूप से उपयोग किया जाता है।
निम्नलिखित आंकड़े बताते हैं कि स्टब मिलान कैसे दिखते हैं।
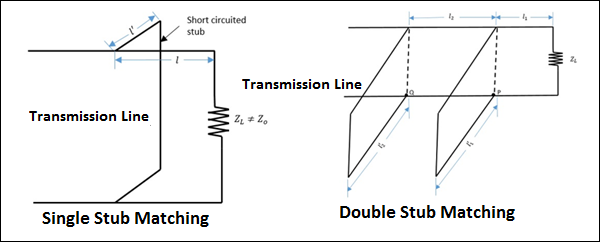
एकल स्टब मिलान और डबल स्टब मिलान, जैसा कि उपरोक्त आंकड़ों में दिखाया गया है, प्रतिबाधा मिलान प्राप्त करने के लिए ट्रांसमिशन लाइनों में किया जाता है।