माइक्रोवेव इंजीनियरिंग - वेवगाइड्स
आमतौर पर, यदि सिग्नल की आवृत्ति या किसी विशेष बैंड की सिग्नल अधिक होती है, तो बैंडविड्थ का उपयोग अधिक होता है क्योंकि सिग्नल अन्य सिग्नलों को संचित होने के लिए अधिक स्थान प्रदान करता है। हालाँकि, हाई फ्रीक्वेंसी सिग्नल बिना अटैच किए लंबी दूरी की यात्रा नहीं कर सकते हैं। हमने अध्ययन किया है कि ट्रांसमिशन लाइनें लंबी दूरी की यात्रा करने में संकेतों की मदद करती हैं।
माइक्रोवेव माइक्रोवेव सर्किट, घटकों और उपकरणों के माध्यम से प्रचार करते हैं, जो माइक्रोवेव ट्रांसमिशन लाइनों के एक हिस्से के रूप में कार्य करते हैं, जिसे मोटे तौर पर वेवगाइड्स कहा जाता है।
ट्यूब की आंतरिक दीवारों से क्रमिक प्रतिबिंबों द्वारा विद्युत चुम्बकीय तरंगों को संचारित करने के लिए एक समान क्रॉस-सेक्शन का एक खोखला धात्विक ट्यूब एक कहलाता है Waveguide।
निम्नलिखित आंकड़ा एक वेवगाइड का एक उदाहरण दिखाता है।
माइक्रोवेव संचार में एक वेवगाइड आमतौर पर पसंद किया जाता है। वेवगाइड ट्रांसमिशन लाइन का एक विशेष रूप है, जो एक खोखली धातु की नली है। ट्रांसमिशन लाइन के विपरीत, एक वेवगाइड में कोई केंद्र कंडक्टर नहीं है।
वेवगाइड की मुख्य विशेषताएं हैं -
ट्यूब दीवार वितरित अधिष्ठापन प्रदान करता है।
ट्यूब की दीवारों के बीच की खाली जगह वितरित समाई प्रदान करती है।
ये भारी और महंगे हैं।
वेवगाइड्स के लाभ
वेवगाइड्स के कुछ फायदे निम्नलिखित हैं।
वेवगाइड्स का निर्माण आसान है।
वे बहुत बड़ी शक्ति (किलो वाट में) संभाल सकते हैं।
वेवगाइड्स में बिजली की हानि बहुत नगण्य है।
वे बहुत कम नुकसान (अल्फा-क्षीणन का कम मूल्य) प्रदान करते हैं।
जब माइक्रोवेव ऊर्जा वेवगाइड के माध्यम से यात्रा करती है, तो यह एक समाक्षीय केबल की तुलना में कम नुकसान का अनुभव करती है।
वेवगाइड्स के प्रकार
पांच प्रकार के वेवगाइड हैं।
- आयताकार तरंग
- वृताकार तरंग
- अण्डाकार तरंग
- एकल-सवार तरंग
- डबल-राइडेड वेवगाइड
निम्नलिखित आंकड़े तरंगों के प्रकार को दर्शाते हैं।
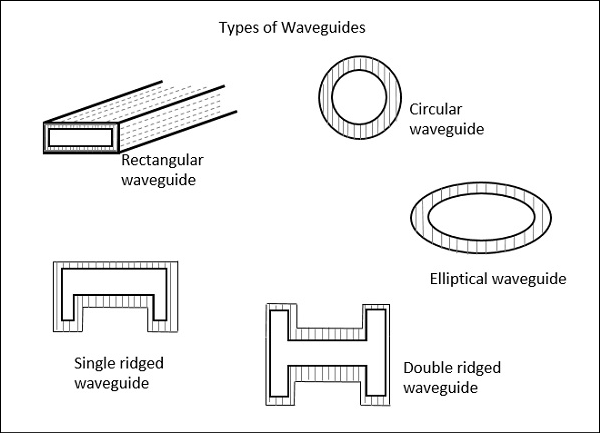
ऊपर दिखाए गए वेवगाइड के प्रकार केंद्र में खोखले होते हैं और तांबे की दीवारों से बने होते हैं। इनकी भीतरी सतह पर Au या Ag की एक पतली परत होती है।
आइए अब हम ट्रांसमिशन लाइनों और वेवगाइड की तुलना करें।
ट्रांसमिशन लाइन्स बनाम वेवगाइड्स
ट्रांसमिशन लाइन और वेव गाइड के बीच मुख्य अंतर है -
ए two conductor structure जो TEM तरंग का समर्थन कर सकता है वह एक ट्रांसमिशन लाइन है।
ए one conductor structure जो TE तरंग या TM तरंग का समर्थन कर सकते हैं लेकिन TEM तरंग को वेवगाइड नहीं कहा जाता है।
निम्न तालिका ट्रांसमिशन लाइनों और वेवगाइड्स के बीच के अंतर को सामने लाती है।
| पारेषण रेखाएँ | waveguides |
|---|---|
| मंदिर तरंग का समर्थन करता है | TEM तरंग का समर्थन नहीं कर सकता |
| सभी आवृत्तियों से गुजर सकते हैं | केवल वे आवृत्तियाँ जो कट-ऑफ़ फ़्रीक्वेंसी से अधिक होती हैं, गुजर सकती हैं |
| दो कंडक्टर ट्रांसमिशन | एक कंडक्टर ट्रांसमिशन |
| प्रतिबिंब कम हैं | एक लहर वेवगाइड की दीवारों से प्रतिबिंब के माध्यम से यात्रा करती है |
| इसकी एक विशेषता प्रतिबाधा है | इसमें तरंग प्रतिबाधा है |
| तरंगों का प्रसार "सर्किट सिद्धांत" के अनुसार है | तरंगों का प्रसार "फील्ड सिद्धांत" के अनुसार है |
| इसमें पृथ्वी पर एक रिटर्न कंडक्टर है | रिटर्न कंडक्टर की आवश्यकता नहीं है क्योंकि वेवगाइड का शरीर पृथ्वी के रूप में कार्य करता है |
| बैंडविड्थ सीमित नहीं है | बैंडविड्थ सीमित है |
| तरंगें फैलती नहीं हैं | लहरें बिखर जाती हैं |
चरण वेग
फेज वेलोसिटी वह दर है, जिस पर तरंग अपने चरण को बदल देती है ताकि फेज शिफ्ट हो सके 2πरेडियंस। इसे एक साइन लहर के तरंग घटकों के वेग में परिवर्तन के रूप में समझा जा सकता है, जब इसे संशोधित किया जाता है।
चरण वेग के लिए एक समीकरण प्राप्त करते हैं।
परिभाषा के अनुसार, चरण की दर पर परिवर्तन होता है 2π रेडियंस पर विचार किया जाना है।
जिसका मतलब है, $λ$ / $T$ इसलिये,
$ $ V = \ frac {\ lambda} {T} $$
कहाँ पे,
$ λ $ = तरंग दैर्ध्य और $ T $ = समय
$ $ V = \ frac {\ lambda} {T} = \ lambda f $$
चूंकि $ f = \ frac {1} {T} $
यदि हम अंश और हर को गुणा करते हैं 2π तो हमारे पास हैं
$ $ V = \ lambda f = \ frac {2 \ pi \ lambda f} {2 \ pi} 5%
हम जानते हैं कि $ \ omega = 2 \ pi f $ है and $ \ बीटा = \ frac {2 \ pi} {f} $
उपरोक्त समीकरण के रूप में लिखा जा सकता है,
$ $ V = \ frac {2 \ pi f} {\ frac {2 \ pi} {\ lambda}} = = \ frac {\ _ omega} {\ beta} $ $
इसलिए, चरण वेग के समीकरण को इस रूप में दर्शाया गया है
$ $ V_p = \ frac {\ omega} {\ beta} $ $
समूह वेग
ग्रुप वेलोसिटी को उस दर के रूप में परिभाषित किया जा सकता है जिस पर तरंग वेवगाइड के माध्यम से फैलती है। इसे उस दर के रूप में समझा जा सकता है जिस पर एक संशोधित लिफाफा अकेले वाहक की तुलना में यात्रा करता है। यह संग्राहक तरंग वेवगाइड के माध्यम से यात्रा करता है।
समूह वेग के समीकरण को इस रूप में दर्शाया गया है
$ $ V_g = \ frac {d \ omega} {d \ beta} $ $
संग्राहक लिफाफे का वेग आमतौर पर वाहक संकेत की तुलना में धीमा होता है।