अभिसरण क्षेत्र (ROC)
The की भिन्नता, जिसके लिए लाप्लास रूपांतरित होता है, अभिसरण का क्षेत्र कहलाता है।
लाप्लास ट्रांसफ़ॉर्म के आरओसी के गुण
आरओसी में एस-प्लेन में j in अक्ष के समानांतर पट्टी रेखाएँ होती हैं।

यदि x (t) बिल्कुल अभिन्न है और यह परिमित अवधि का है, तो ROC संपूर्ण s- समतल है।
यदि x (t) एक सही पक्षीय अनुक्रम है तो ROC: Re {s}> t o ।
यदि x (t) एक बाएं तरफा अनुक्रम है तो ROC: Re {s} <t o ।
यदि x (t) दो तरफा अनुक्रम है तो ROC दो क्षेत्रों का संयोजन है।
नीचे दिए गए उदाहरणों का उपयोग करके आरओसी की व्याख्या की जा सकती है:
Example 1: Find the Laplace transform and ROC of $x(t) = e-^{at}u(t)$
$L.T[x(t)] = L.T[e-^{at}u(t)] = {1 \over S+a}$
$ Re{} \gt -a $
$ ROC:Re{s} \gt >-a$

Example 2: Find the Laplace transform and ROC of $x(t) = e^{at}u(-t)$
$ L.T[x(t)] = L.T[e^{at}u(t)] = {1 \over S-a} $
$ Re{s} < a $
$ ROC: Re{s} < a $

Example 3: Find the Laplace transform and ROC of $x(t) = e^{-at}u(t)+e^{at}u(-t)$
$L.T[x(t)] = L.T[e^{-at}u(t)+e^{at}u(-t)] = {1 \over S+a} + {1 \over S-a}$
के लिये ${1 \over S+a} Re\{s\} \gt -a $
के लिये ${1 \over S-a} Re\{s\} \lt a $

उपरोक्त आरेख का उल्लेख करते हुए, संयोजन क्षेत्र से-ए तक निहित है। इसलिये,
$ ROC: -a < Re{s} < a $
कारण और स्थिरता
एक कार्य-प्रणाली के कारण, इसके स्थानांतरण कार्य के सभी खंभे s- समतल के ठीक आधे होने चाहिए।

एक प्रणाली को स्थिर कहा जाता है जब इसके स्थानांतरण फ़ंक्शन के सभी पोल एस-प्लेन के बाईं ओर स्थित होते हैं।

किसी सिस्टम को अस्थिर तब कहा जाता है जब उसके ट्रांसफ़र फ़ंक्शन के कम से कम एक पोल को एस-प्लेन के दाहिने आधे हिस्से में स्थानांतरित कर दिया जाता है।
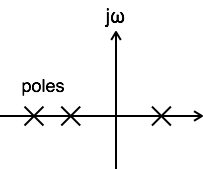
किसी सिस्टम को उस समय स्थिर कहा जाता है जब उसके स्थानांतरण फ़ंक्शन का कम से कम एक ध्रुव एस-प्लेन के said अक्ष पर होता है।

बेसिक फंक्शंस का आर.ओ.सी.
| च (टी) | एफ (रों) | रूह |
|---|---|---|
| $u(t)$ | $${1\over s}$$ | ROC: Re {s}> 0 |
| $ t\, u(t) $ | $${1\over s^2} $$ | ROC: Re {s}> 0 |
| $ t^n\, u(t) $ | $$ {n! \over s^{n+1}} $$ | ROC: Re {s}> 0 |
| $ e^{at}\, u(t) $ | $$ {1\over s-a} $$ | ROC: Re {s}> a |
| $ e^{-at}\, u(t) $ | $$ {1\over s+a} $$ | ROC: Re {s}> -a |
| $ e^{at}\, u(t) $ | $$ - {1\over s-a} $$ | ROC: Re {s} <a |
| $ e^{-at}\, u(-t) $ | $$ - {1\over s+a} $$ | ROC: Re {s} <-a |
| $ t\, e^{at}\, u(t) $ | $$ {1 \over (s-a)^2} $$ | ROC: Re {s}> a |
| $ t^{n} e^{at}\, u(t) $ | $$ {n! \over (s-a)^{n+1}} $$ | ROC: Re {s}> a |
| $ t\, e^{-at}\, u(t) $ | $$ {1 \over (s+a)^2} $$ | ROC: Re {s}> -a |
| $ t^n\, e^{-at}\, u(t) $ | $${n! \over (s+a)^{n+1}} $$ | ROC: Re {s}> -a |
| $ t\, e^{at}\, u(-t) $ | $$ - {1 \over (s-a)^2} $$ | ROC: Re {s} <a |
| $ t^n\, e^{at}\, u(-t) $ | $$ - {n! \over (s-a)^{n+1}} $$ | ROC: Re {s} <a |
| $ t\, e^{-at}\,u(-t) $ | $$ - {1 \over (s+a)^2} $$ | ROC: Re {s} <-a |
| $ t^n\, e^{-at}\, u(-t) $ | $$ - {n! \over (s+a)^{n+1}} $$ | ROC: Re {s} <-a |
| $ e^{-at} \cos \, bt $ | $$ {s+a \over (s+a)^2 + b^2 } $$ | |
| $ e^{-at} \sin\, bt $ | $$ {b \over (s+a)^2 + b^2 } $$ |