जेड-ट्रांसफॉर्म गुण
Z- ट्रांसफॉर्म में निम्नलिखित गुण होते हैं:
रैखिकता संपत्ति
यदि $ \ _, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
और $ $, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
फिर रैखिकता संपत्ति कहती है कि
$ a, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a a, X (Z) + b \ _, Y (Z) $
समय स्थानांतरण संपत्ति
यदि $ \ _, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
फिर टाइम शिफ्टिंग प्रॉपर्टी बताती है कि
$ x (nm) \ stackrel {\ _ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $
घातीय अनुक्रम संपत्ति द्वारा गुणन
यदि $ \ _, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
फिर एक घातीय अनुक्रम गुण द्वारा गुणन बताता है कि
$ a ^ n \ _। x (n) \ stackrel {\ _ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $
समय उत्क्रमण संपत्ति
यदि $ \ _, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
तब समय उलट संपत्ति बताता है कि
$ x (एन) \ स्टैकेल {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $
Z संपत्ति में Z- डोमेन या गुणन में अंतर
यदि $ \ _, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
फिर z-domain प्रॉपर्टी में n या विभेदन द्वारा गुणा करना बताता है कि
$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ over dZ ^ K} $
कनवल्शन प्रॉपर्टी
यदि $ \ _, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
और $ $, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
फिर दोषी संपत्ति बताते हैं कि
$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $।
सहसंबंध संपत्ति
यदि $ \ _, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
और $ $, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
तब सहसंबंध संपत्ति बताती है कि
$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $।
प्रारंभिक मूल्य और अंतिम मूल्य सिद्धांत
Z- परिवर्तन के प्रारंभिक मूल्य और अंतिम मूल्य प्रमेय कार्य-संकेत के लिए परिभाषित किए गए हैं।
प्रारंभिक मूल्य प्रमेय
एक कारण संकेत x (n) के लिए, प्रारंभिक मूल्य प्रमेय बताता है कि
$ x (0) = \ lim_ {z \ to to infty} zX (z) $
इसका उपयोग उलटा जेड-ट्रांसफ़ॉर्म लेने के बिना सिग्नल के प्रारंभिक मूल्य को खोजने के लिए किया जाता है
अंतिम मूल्य प्रमेय
कारण संकेत x (n) के लिए, अंतिम मान प्रमेय बताता है कि
$ x (\ infty) = \ lim_ {z \ to 1} [z-1] (X (z) $
इसका उपयोग उलटा जेड-ट्रांसफ़ॉर्म किए बिना सिग्नल के अंतिम मूल्य को खोजने के लिए किया जाता है।
Z- ट्रांसफॉर्म का कन्वर्जेंस (ROC) क्षेत्र
Z की भिन्नता की सीमा, जिसके लिए z- रूपांतरित रूपांतरों को z- रूपान्तरण के अभिसरण का क्षेत्र कहा जाता है।
जेड-ट्रांसफॉर्म के आरओसी के गुण
जेड-ट्रांसफॉर्मेशन के आरओसी को जेड-प्लेन में सर्कल के साथ दर्शाया गया है।
आरओसी में कोई पोल नहीं है।
यदि x (n) एक परिमित अवधि कारण अनुक्रम या दाएं तरफा अनुक्रम है, तो ROC केवल 0 = 0 को छोड़कर संपूर्ण z- समतल है।
यदि x (n) एक परिमित अवधि विरोधी कारण अनुक्रम या बाएं तरफा अनुक्रम है, तो ROC, z = ∞ को छोड़कर संपूर्ण z- समतल है।
यदि x (n) एक अनंत अवधि कारण अनुक्रम है, तो ROC त्रिज्या aie के साथ सर्कल के बाहरी है। z | > ए।
यदि x (n) एक अनंत अवधि विरोधी कारण अनुक्रम है, तो ROC त्रिज्या aie-z के साथ वृत्त का आंतरिक भाग है। <क।
यदि x (n) एक परिमित अवधि दो तरफा अनुक्रम है, तो ROC, z = 0 & z = at को छोड़कर संपूर्ण z- समतल है।
आरओसी की अवधारणा को निम्नलिखित उदाहरण द्वारा समझाया जा सकता है:
Example 1: Z- परिवर्तन और $ a ^ nu [n] + a ^ {-} nu [-n-1] $ का ROC खोजें
$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ over Za} + {Z \ over Z {-1 \ over a}} $
$ $ आरओसी: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ a} $ $
ROC के कथानक में दो शर्तें हैं> 1 और <1, जैसा कि आप नहीं जानते हैं।

इस मामले में, कोई संयोजन आरओसी नहीं है।
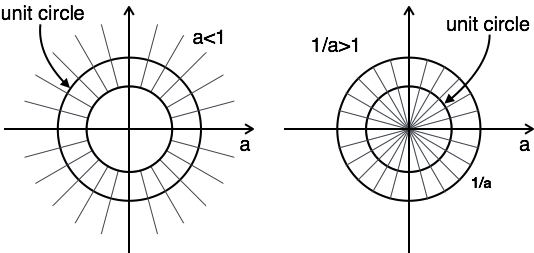
यहाँ, ROC का संयोजन $ a \ lt | z | \ lt {1 \ a} $
इसलिए इस समस्या के लिए, z- परिवर्तन संभव है जब एक <1।
कारण और स्थिरता
असतत समय एलटीआई प्रणाली के लिए कारणों की स्थिति इस प्रकार है:
एक असतत समय LTI प्रणाली जब कारण है
ROC सबसे बाहरी ध्रुव के बाहर है।
ट्रांसफर फ़ंक्शन H [Z] में, अंश का क्रम हर के क्रम से कम नहीं हो सकता है।
असतत समय एलटीआई सिस्टम के लिए स्थिरता की स्थिति
एक असतत समय एलटीआई प्रणाली स्थिर है जब
इसका सिस्टम फंक्शन H [Z] में यूनिट सर्कल शामिल है | z = = 1 |
ट्रांसफर फ़ंक्शन के सभी पोल यूनिट सर्कल के अंदर रखे जाते हैं | z | = 1।
बेसिक सिग्नल का Z- ट्रांसफॉर्म
| एक्स (टी) | एक्स [Z] |
|---|---|
| \ डेल्टा $ $ | 1 |
| यू $ (एन) $ | $ {Z \ ओवर Z-1} $ |
| यू $ (-n -1) $ | $ - {Z \ over Z-1} $ |
| $ \ डेल्टा (एनएम) $ | $ Z ^ {- मीटर} $ |
| एक ^ न्यू [n] $ $ | $ {Z \ _ ज़रा} $ |
| एक ^ न्यू $ [-n-1] $ | $ - {Z \ over Za} $ |
| $ N \, एक ^ न्यू [n] $ | $ {aZ \ over | Za | ^ 2} $ |
| $ n \ _, ए ^ नु [-n-1] $ | $ - {aZ \ over | ज़ा | ^ 2} $ |
| $ a ^ n \ cos \ omega nu [n] $ | $ {Z ^ 2-aZ \ cos \ omega \ ओवर Z ^ 2-2aZ \ cos \ omega + a ^ 2} $ |
| $ a ^ n \ sin \ omega nu [n] $ | $ {aZ \ sin \ omega \ _ Z ^ 2 -2aZ \ cos \ omega + a ^ 2 2% |