वृत्त का चतुर्थ भाग में रेखांकन 1

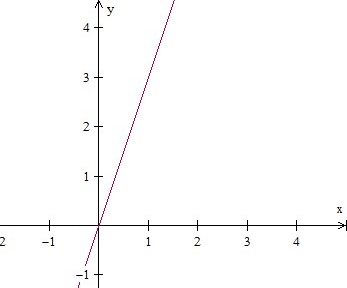
हम एक पंक्ति का रेखांकन करते हैं जिसका समीकरण दिया गया है, उदाहरण के लिए y = 3x कहें। हमें लाइन को रेखांकन करने के लिए कम से कम दो अंक चाहिए या जोड़े का आदेश देना चाहिए। पहले हम कुछ x मान चुनते हैं। तब हम x के प्रत्येक मान के लिए y = 3x का मूल्यांकन करते हैं।

उदाहरण के लिए x = 0, y = 3 (0) = 0; x = 1, y = 3 (1) = 3 और इसी तरह। हमने एक्स, वाई और आदेशित जोड़ी (एक्स, वाई) मूल्यों को निम्नानुसार रखा।

एक्स	y	(एक्स, वाई)
0	३ (०) = ०	(0,0)
1	3 (1) = 3	(1,3)
2	3 (2) = 6	(2,6)
3	३ (३) = ९	(3,9)
4	3 (4) = 12	(4,12)

हम देखते हैं कि आदेशित जोड़े चतुर्भुज में झूठ बोलते हैं। 1. बिंदुओं में शामिल होने से चतुर्थांश 1 में रेखा का ग्राफ मिलेगा।

चतुष्कोण 1 में रेखा का रेखांकन करें, जिसका समीकरण नीचे दिया गया है।

2x - y = 3

उपाय

Step 1:

दिए गए समीकरण 2x - y = 3; y = 0, x = 3/2 के लिए; x = 2, y = 2 (2) –3 = 4–3 = 1. के लिए दो आर्डर किए गए जोड़े हैं (3/2, 0) (2, 1)

Step 2:

बिंदुओं को प्लॉट करना और हमें मिलने वाली रेखा के साथ जुड़ना

चतुष्कोण 1 में रेखा का रेखांकन करें, जिसका समीकरण नीचे दिया गया है।

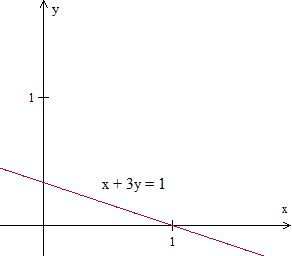
x + 3y = 1

उपाय

Step 1:

दिया गया समीकरण x + 3y = 1; y = 0, x = 1 के लिए; X = 0 के लिए, y = 1/3। तो दो आदेशित जोड़े हैं (1, 0) और (0, 1/3)

Step 2:

बिंदुओं को प्लॉट करना और हमें मिलने वाली रेखा के साथ जुड़ना