Struktur Data dan Algoritma - Array

Array adalah wadah yang dapat menampung sejumlah item tetap dan item ini harus berjenis sama. Sebagian besar struktur data menggunakan array untuk mengimplementasikan algoritme mereka. Berikut adalah istilah-istilah penting untuk memahami konsep Array.

Element - Setiap item yang disimpan dalam array disebut elemen.
Index - Setiap lokasi elemen dalam array memiliki indeks numerik, yang digunakan untuk mengidentifikasi elemen.

Representasi Array

Array dapat dideklarasikan dengan berbagai cara dalam berbagai bahasa. Sebagai ilustrasi, mari kita ambil deklarasi array C.

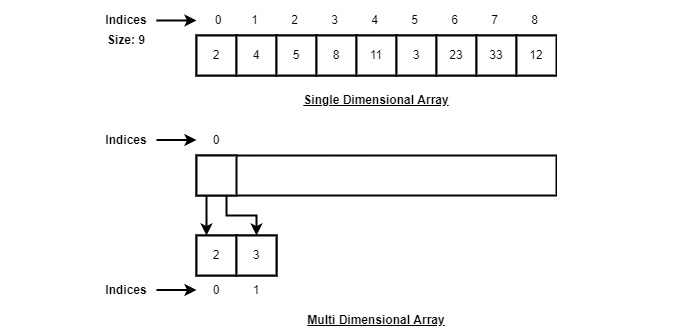
Sesuai ilustrasi di atas, berikut adalah poin-poin penting yang harus diperhatikan.

Indeks dimulai dengan 0.
Panjang larik adalah 10 yang artinya dapat menyimpan 10 elemen.
Setiap elemen dapat diakses melalui indeksnya. Misalnya, kita dapat mengambil elemen di indeks 6 sebagai 9.

Operasi Dasar

Berikut adalah operasi dasar yang didukung oleh sebuah array.

Traverse - cetak semua elemen array satu per satu.
Insertion - Menambahkan elemen pada indeks yang diberikan.
Deletion - Menghapus elemen pada indeks yang diberikan.
Search - Mencari elemen menggunakan indeks yang diberikan atau berdasarkan nilainya.
Update - Memperbarui elemen pada indeks yang diberikan.

Di C, ketika sebuah array diinisialisasi dengan ukuran, maka itu memberikan nilai default ke elemennya dalam urutan berikut.

Tipe data	Nilai Default
bool	Salah
arang	0
int	0
mengapung	0.0
dua kali lipat	0.0f
kosong
wchar_t	0

Operasi Traverse

Operasi ini untuk melintasi elemen-elemen array.

Contoh

Program berikut melintasi dan mencetak elemen dari sebuah array:

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;   
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Ketika kita mengkompilasi dan menjalankan program di atas, hasilnya adalah sebagai berikut:

Keluaran

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

Operasi Penyisipan

Operasi sisipkan adalah memasukkan satu atau lebih elemen data ke dalam larik. Berdasarkan persyaratan, elemen baru dapat ditambahkan di awal, akhir, atau indeks larik apa pun.

Di sini, kita melihat implementasi praktis dari operasi penyisipan, di mana kita menambahkan data di akhir larik -

Contoh

Berikut adalah implementasi dari algoritma di atas -

#include <stdio.h>

main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   
   printf("The original array elements are :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }

   n = n + 1;
	
   while( j >= k) {
      LA[j+1] = LA[j];
      j = j - 1;
   }

   LA[k] = item;

   printf("The array elements after insertion :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Ketika kita mengkompilasi dan menjalankan program di atas, hasilnya adalah sebagai berikut:

Keluaran

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after insertion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 10 
LA[4] = 7 
LA[5] = 8

Untuk variasi lain dari operasi penyisipan larik, klik di sini

Operasi Penghapusan

Penghapusan mengacu pada penghapusan elemen yang ada dari larik dan mengatur ulang semua elemen larik.

Algoritma

Mempertimbangkan LA adalah array linier dengan N elemen dan K adalah bilangan bulat positif sehingga K<=N. Berikut adalah algoritma untuk menghapus elemen yang tersedia di K ^th posisi LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

Contoh

Berikut adalah implementasi dari algoritma di atas -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   j = k;
	
   while( j < n) {
      LA[j-1] = LA[j];
      j = j + 1;
   }
	
   n = n -1;
   
   printf("The array elements after deletion :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Ketika kita mengkompilasi dan menjalankan program di atas, hasilnya adalah sebagai berikut:

Keluaran

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after deletion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 7 
LA[3] = 8

Operasi Pencarian

Anda dapat melakukan pencarian elemen array berdasarkan nilainya atau indeksnya.

Algoritma

Mempertimbangkan LA adalah array linier dengan N elemen dan K adalah bilangan bulat positif sehingga K<=N. Berikut algoritma untuk mencari elemen dengan nilai ITEM menggunakan pencarian sekuensial.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Contoh

Berikut adalah implementasi dari algoritma di atas -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   while( j < n){
      if( LA[j] == item ) {
         break;
      }
		
      j = j + 1;
   }
	
   printf("Found element %d at position %d\n", item, j+1);
}

Ketika kita mengkompilasi dan menjalankan program di atas, hasilnya adalah sebagai berikut:

Keluaran

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
Found element 5 at position 3

Perbarui Operasi

Operasi pembaruan mengacu pada pembaruan elemen yang ada dari larik pada indeks tertentu.

Algoritma

Mempertimbangkan LA adalah array linier dengan N elemen dan K adalah bilangan bulat positif sehingga K<=N. Berikut adalah algoritma untuk memperbarui elemen yang tersedia di K ^th posisi LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Contoh

Berikut adalah implementasi dari algoritma di atas -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   LA[k-1] = item;

   printf("The array elements after updation :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Ketika kita mengkompilasi dan menjalankan program di atas, hasilnya adalah sebagai berikut:

Keluaran

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after updation :
LA[0] = 1 
LA[1] = 3 
LA[2] = 10 
LA[3] = 7 
LA[4] = 8