Struktur Data dan Algoritma - Pohon AVL

Bagaimana jika masukan ke pohon pencarian biner datang dengan cara yang diurutkan (menaik atau menurun)? Kemudian akan terlihat seperti ini -

Teramati bahwa kinerja kasus terburuk BST paling dekat dengan algoritma pencarian linier, yaitu Ο (n). Dalam data real-time, kita tidak dapat memprediksi pola data dan frekuensinya. Jadi, muncul kebutuhan untuk mengimbangi BST yang ada.

Dinamai menurut penemunya Adelson, Velski & Landis, AVL treesadalah pohon pencarian biner penyeimbang ketinggian. Pohon AVL memeriksa ketinggian sub-pohon kiri dan kanan dan memastikan bahwa perbedaannya tidak lebih dari 1. Perbedaan ini disebutBalance Factor.

Di sini kita melihat bahwa pohon pertama seimbang dan dua pohon berikutnya tidak seimbang -

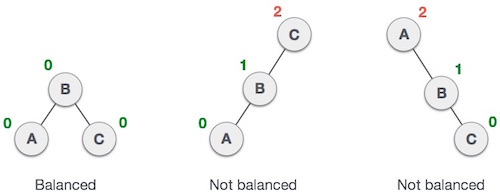
Di pohon kedua, subtree kiri dari C memiliki tinggi 2 dan subtree kanan memiliki tinggi 0, jadi selisihnya adalah 2. Pada pohon ketiga, subtree kanan Amemiliki tinggi 2 dan kiri hilang, jadi 0, dan perbedaannya adalah 2 lagi. Pohon AVL mengizinkan perbedaan (faktor keseimbangan) menjadi hanya 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Jika selisih ketinggian sub-pohon kiri dan kanan lebih dari 1, pohon tersebut diimbangi dengan beberapa teknik rotasi.

Rotasi AVL

Untuk menyeimbangkan dirinya sendiri, pohon AVL dapat melakukan empat jenis rotasi berikut -

• Rotasi kiri
• Rotasi yang tepat
• Rotasi Kiri-Kanan
• Rotasi Kanan-Kiri

Dua rotasi pertama adalah rotasi tunggal dan dua rotasi berikutnya adalah rotasi ganda. Untuk memiliki pohon yang tidak seimbang, paling tidak kita membutuhkan pohon dengan tinggi 2. Dengan pohon sederhana ini mari kita pahami satu persatu.

Rotasi Kiri

Jika sebuah pohon menjadi tidak seimbang, ketika sebuah simpul dimasukkan ke dalam sub-pohon kanan dari sub-pohon kanan, maka kami melakukan satu rotasi kiri -

Dalam contoh kami, node Atelah menjadi tidak seimbang saat sebuah node disisipkan di subpohon kanan dari subpohon kanan A. Kami melakukan rotasi kiri dengan membuatA sub-pohon kiri dari B.

Rotasi Kanan

Pohon AVL mungkin menjadi tidak seimbang, jika sebuah node disisipkan di subpohon kiri dari subpohon kiri. Pohon itu kemudian membutuhkan rotasi yang tepat.

Seperti yang digambarkan, simpul yang tidak seimbang menjadi anak kanan dari anak kirinya dengan melakukan rotasi ke kanan.

Rotasi Kiri-Kanan

Rotasi ganda adalah versi yang agak rumit dari versi rotasi yang sudah dijelaskan. Untuk memahaminya dengan lebih baik, kita harus mencatat setiap tindakan yang dilakukan saat rotasi. Pertama mari kita periksa bagaimana melakukan rotasi Kiri-Kanan. Rotasi kiri-kanan adalah kombinasi dari rotasi kiri diikuti dengan rotasi kanan.

Negara	Tindakan
	Sebuah node telah disisipkan ke sub pohon kanan dari sub pohon kiri. Ini membuatCnode yang tidak seimbang. Skenario ini menyebabkan pohon AVL melakukan rotasi kiri-kanan.
	Kami pertama kali melakukan rotasi kiri di subpohon kiri C. Ini membuatA, subtree kiri dari B.
	Node C masih tidak seimbang, namun sekarang, itu karena subtree kiri dari subtree kiri.
	Sekarang kita akan memutar pohon ke kanan, membuatnya B simpul akar baru dari subpohon ini. C sekarang menjadi subtree kanan dari subtree kirinya sendiri.
	Pohon itu sekarang seimbang.

Rotasi Kanan-Kiri

Jenis rotasi ganda kedua adalah Rotasi Kanan-Kiri. Ini adalah kombinasi dari rotasi kanan diikuti dengan rotasi kiri.

Negara	Tindakan
	Sebuah node telah disisipkan ke subpohon kiri dari subpohon kanan. Ini membuatA, simpul tidak seimbang dengan faktor keseimbangan 2.
	Pertama, kami melakukan rotasi yang benar C simpul, membuat C subtree kanan dari subtree kirinya sendiri B. Sekarang,B menjadi subtree kanan dari A.
	Node A masih tidak seimbang karena subtree kanan dari subtree kanan dan membutuhkan rotasi kiri.
	Rotasi kiri dilakukan dengan membuat B simpul akar baru dari subpohon. A menjadi subtree kiri dari subtree kanannya B.
	Pohon itu sekarang seimbang.