Jembatan AC
Pada bab ini, mari kita bahas tentang jembatan AC, yang dapat digunakan untuk mengukur induktansi. Jembatan AC beroperasi hanya dengan sinyal tegangan AC. Itucircuit diagram Jembatan AC ditunjukkan pada gambar di bawah ini.
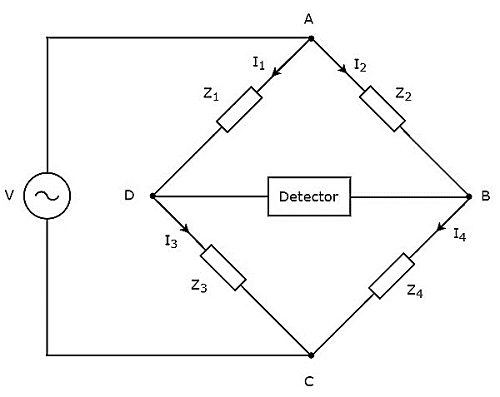
Seperti yang ditunjukkan pada gambar di atas, jembatan AC terutama terdiri dari empat lengan, yang dihubungkan dalam belah ketupat atau square shape. Semua lengan ini terdiri dari beberapa impedansi.
Detektor dan sumber tegangan AC juga diperlukan untuk menemukan nilai impedansi yang tidak diketahui. Oleh karena itu, salah satu dari keduanya ditempatkan pada satu diagonal jembatan AC dan yang lainnya ditempatkan pada diagonal jembatan AC lainnya. Kondisi keseimbangan jembatan Wheatstone sebagai -
$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
Kami akan mendapatkan balancing condition of AC bridge, hanya dengan mengganti R dengan Z pada persamaan di atas.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $
Di sini, $ Z_ {1} $ dan $ Z_ {2} $ adalah impedansi tetap. Padahal, $ Z_ {3} $ adalah impedansi variabel standar dan $ Z_ {4} $ adalah impedansi yang tidak diketahui.
Note - Kita dapat memilih dua dari empat impedansi tersebut sebagai impedansi tetap, satu impedansi sebagai impedansi variabel standar & impedansi lainnya sebagai impedansi yang tidak diketahui berdasarkan aplikasi.
Berikut dua jembatan AC yang bisa digunakan untuk mengukur inductance.
- Jembatan Maxwell
- Jembatan Hay
Nah, mari kita bahas tentang dua jembatan AC ini satu per satu.
Jembatan Maxwell
Jembatan Maxwell adalah jembatan AC yang memiliki empat lengan, yang dihubungkan dalam bentuk belah ketupat atau square shape. Dua lengan jembatan ini terdiri dari satu resistor, satu lengan terdiri dari rangkaian rangkaian resistor dan induktor & lengan lainnya terdiri dari kombinasi paralel resistor dan kapasitor.
Detektor AC dan sumber tegangan AC digunakan untuk mencari nilai impedansi yang tidak diketahui. Oleh karena itu, salah satu dari keduanya ditempatkan di satu diagonal jembatan Maxwell dan yang lainnya ditempatkan di diagonal lain jembatan Maxwell.
Jembatan Maxwell digunakan untuk mengukur nilai induktansi sedang. Itucircuit diagram Jembatan Maxwell ditunjukkan pada gambar di bawah ini.
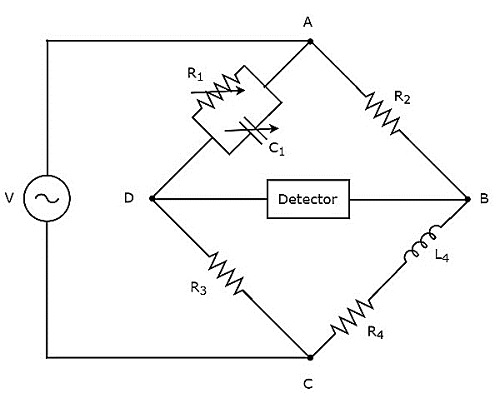
Pada rangkaian di atas, lengan AB, BC, CD dan DA bersama-sama membentuk belah ketupat atau persegi. Lengan AB dan CD masing-masing terdiri dari resistor, $ R_ {2} $ dan $ R_ {3} $. Lengan, BC terdiri dari kombinasi seri resistor, $ R_ {4} $ dan induktor, $ L_ {4} $. Lengan, DA terdiri dari kombinasi paralel resistor, $ R_ {1} $ dan kapasitor, $ C_ {1} $.
Misalkan, $ Z_ {1}, Z_ {2}, Z_ {3} $ dan $ Z_ {4} $ masing-masing adalah impedansi lengan DA, AB, CD dan BC. Ituvalues of these impedances akan
$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$
$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute Nilai impedansi ini dalam kondisi balancing AC jembatan berikut.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ kiri ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ kanan)} $$
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $
Oleh comparing masing-masing suku nyata dan imajiner persamaan di atas, kita akan mendapatkan
$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ Persamaan 1
$ L_ {4} = C_ {1} R_ {2} R_ {3} $ Persamaan 2
Dengan mengganti nilai resistor $ R_ {1} $, $ R_ {2} $ dan $ R_ {3} $ pada Persamaan 1, kita akan mendapatkan nilai resistor $ R_ {4} $. Demikian pula dengan mengganti nilai kapasitor, $ C_ {1} $ dan nilai resistor, $ R_ {2} $ dan $ R_ {3} $ pada Persamaan 2, kita akan mendapatkan nilai induktor, $ L_ {4 } $.
Itu advantage jembatan Maxwell adalah bahwa kedua nilai resistor, $ R_ {4} $ dan induktor, $ L_ {4} $ tidak tergantung pada nilai frekuensi.
Jembatan Hay
Jembatan Hay adalah versi modifikasi dari jembatan Maxwell, yang kita dapatkan dengan memodifikasi lengan, yang terdiri dari kombinasi paralel resistor dan kapasitor ke lengan, yang terdiri dari rangkaian kombinasi resistor dan kapasitor di jembatan Maxwell.
Jembatan Hay digunakan untuk mengukur nilai induktansi tinggi. Itucircuit diagram jembatan Hay ditunjukkan pada gambar di bawah ini.
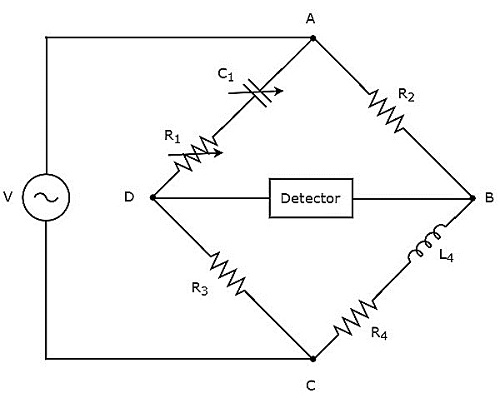
Pada rangkaian di atas, lengan AB, BC, CD dan DA bersama-sama membentuk belah ketupat atau persegi. Lengan, AB dan CD masing-masing terdiri dari resistor, $ R_ {2} $ dan $ R_ {3} $. Lengan, BC terdiri dari kombinasi seri resistor, $ R_ {4} $ dan induktor, $ L_ {4} $. Lengan, DA terdiri dari rangkaian kombinasi resistor, $ R_ {1} $ dan kapasitor, $ C_ {1} $.
Misalkan, $ Z_ {1}, Z_ {2}, Z_ {3} $ dan $ Z_ {4} $ masing-masing adalah impedansi lengan DA, AB, CD dan BC. Ituvalues of these impedances akan
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute Nilai impedansi ini dalam kondisi balancing AC jembatan berikut.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ kiri (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ kanan)} $
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ kiri (1 + j \ omega R_ {1} C_ {1} \ benar)} $
Kalikan pembilang dan penyebut suku ruas kanan persamaan di atas dengan $ 1 - j \ omega R_ {1} C_ {1} $.
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ kiri (1 + j \ omega R_ {1} C_ { 1} \ kanan)} \ times \ frac {\ kiri (1 - j \ omega R_ {1} C_ {1} \ kanan)} {\ kiri (1 - j \ omega R_ {1} C_ {1} \ kanan )} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ omega R_ {2} R_ {3} C_ {1}} {\ kiri (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ kanan)} $
Oleh comparing masing-masing suku nyata dan imajiner persamaan di atas, kita akan mendapatkan
$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ kiri (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Persamaan 3
$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ tersisa (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ kanan)} $ Persamaan 4
Dengan mengganti nilai $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ dan $ \ omega $ pada Persamaan 3 dan Persamaan 4, kita akan mendapatkan nilai resistor, $ R_ {4 } $ dan induktor, $ L_ {4} $.