Jembatan AC Lainnya
Pada bab sebelumnya, kita telah membahas tentang dua jembatan AC yang dapat digunakan untuk mengukur induktansi. Dalam bab ini, mari kita bahas tentang yang berikut initwo AC bridges.
- Jembatan Schering
- Jembatan Wien
Kedua jembatan ini masing-masing dapat digunakan untuk mengukur kapasitansi dan frekuensi.
Jembatan Schering
Jembatan Schering merupakan jembatan AC yang memiliki empat lengan, yang dihubungkan dalam bentuk belah ketupat atau square shape, yang satu lengannya terdiri dari resistor tunggal, satu lengan terdiri dari rangkaian kombinasi resistor dan kapasitor, satu lengan terdiri dari kapasitor tunggal & lengan lainnya terdiri dari kombinasi paralel resistor dan kapasitor.
Detektor AC dan sumber tegangan AC juga digunakan untuk mencari nilai impedansi yang tidak diketahui, maka salah satunya ditempatkan pada satu diagonal jembatan Schering dan satu lagi ditempatkan pada diagonal jembatan Schering yang lain.
Jembatan Schering digunakan untuk mengukur nilai kapasitansi. Itucircuit diagram Jembatan Schering ditunjukkan pada gambar di bawah ini.
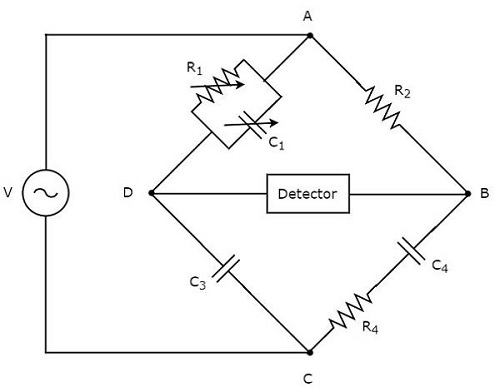
Di sirkuit di atas, lengan AB, BC, CD dan DA bersama-sama membentuk belah ketupat atau square shape. Lengan AB terdiri dari resistor, $ R_ {2} $. Lengan BC terdiri dari kombinasi seri resistor, $ R_ {4} $ dan kapasitor, $ C_ {4} $. CD lengan terdiri dari sebuah kapasitor, $ C_ {3} $. Lengan DA terdiri dari kombinasi paralel resistor, $ R_ {1} $ dan kapasitor, $ C_ {1} $.
Misalkan, $ Z_ {1} $, $ Z_ {2} $, $ Z_ {3} $ dan $ Z_ {4} $ masing-masing adalah impedansi lengan DA, AB, CD, dan BC. Ituvalues of these impedances akan
$ Z_ {1} = \ frac {R_ {1} \ kiri (\ frac {1} {j \ omega C_ {1}} \ kanan)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $
$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $
$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $
$ \ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $
Substitute Nilai impedansi ini dalam kondisi balancing AC jembatan berikut.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ kiri (\ frac {1} {j \ omega C_ { 3}} \ kanan)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ kiri (1 + j \ omega R_ {1} C_ {1} \ kanan)} {j \ omega R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ kanan)} {R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $
Oleh comparing masing-masing suku nyata dan imajiner persamaan di atas, kita akan mendapatkan
$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $ Persamaan 1
$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $ Persamaan 2
Dengan mengganti nilai $ R_ {1}, R_ {2} $ dan $ C_ {3} $ pada Persamaan 1, kita akan mendapatkan nilai kapasitor, $ C_ {4} $. Demikian pula, dengan mengganti nilai $ R_ {2}, C_ {1} $ dan $ C_ {3} $ pada Persamaan 2, kita akan mendapatkan nilai resistor, $ R_ {4} $.
Itu advantage Jembatan Schering adalah bahwa nilai resistor, $ R_ {4} $ dan kapasitor, $ C_ {4} $ tidak tergantung pada nilai frekuensi.
Jembatan Wien
Wien’s bridgemerupakan jembatan AC yang memiliki empat lengan, yang dihubungkan dalam bentuk belah ketupat atau persegi. Diantara dua lengan terdiri dari satu resistor, satu lengan terdiri dari kombinasi paralel resistor dan kapasitor & lengan lainnya terdiri dari rangkaian kombinasi resistor dan kapasitor.
Detektor AC dan sumber tegangan AC juga diperlukan untuk mengetahui nilai frekuensinya. Oleh karena itu, salah satu dari keduanya ditempatkan pada satu diagonal jembatan Wien dan yang lainnya ditempatkan pada diagonal jembatan Wien yang lain.
Itu circuit diagram Jembatan Wien ditunjukkan pada gambar di bawah ini.
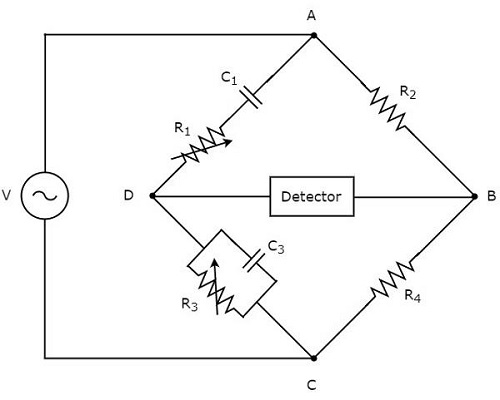
Di sirkuit di atas, lengan AB, BC, CD dan DA bersama-sama membentuk belah ketupat atau square shape. Lengan, AB dan BC masing-masing terdiri dari resistor, $ R_ {2} $ dan $ R_ {4} $. Lengan, CD terdiri dari kombinasi paralel resistor, $ R_ {3} $ dan kapasitor, $ C_ {3} $. Lengan, DA terdiri dari rangkaian kombinasi resistor, $ R_ {1} $ dan kapasitor, $ C_ {1} $.
Misalkan, $ Z_ {1}, Z_ {2}, Z_ {3} $ dan $ Z_ {4} $ masing-masing adalah impedansi lengan DA, AB, CD dan BC. Ituvalues of these impedances akan
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$
$ Z_ {2} = R_ {2} $
$$ Z_ {3} = \ frac {R_ {3} \ kiri (\ frac {1} {j \ omega C_ {3}} \ kanan)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$
$$ \ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$
$ Z_ {4} = R_ {4} $
Substitute Nilai impedansi ini dalam kondisi balancing AC jembatan berikut.
$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$
$$ \ kiri (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ kanan) R_ {4} = R_ {2} \ kiri (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ kanan) $$
$ \ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow \ left (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ kanan) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow R_ {4} \ kiri (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ kanan) + j \ omega R_ {4} \ kiri (R_ {3} C_ {3} + R_ {1} C_ {1} \ kanan) = j \ omega C_ {1} R_ {2} R_ {3} $
Equate masing-masing real terms dari persamaan di atas.
$$ R_ {4} \ kiri (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ kanan) = 0 $$
$ \ Rightarrow 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $
$ \ Rightarrow 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $
$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
Substitute, $ \ omega = 2 \ pi f $ dalam persamaan di atas.
$$ \ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$
$ \ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
Kita dapat mencari nilai frekuensi $ f $ sumber tegangan AC dengan mengganti nilai $ R_ {1}, R_ {3}, C_ {1} $ dan $ C_ {3} $ pada persamaan di atas.
Jika $ R_ {1} = R_ {3} = R $ dan $ C_ {1} = C_ {3} = C $, maka kita dapat mencari nilai frekuensi $ f $ dari sumber tegangan AC dengan menggunakan rumus berikut .
$$ f = \ frac {1} {2 \ pi RC} $$
Jembatan Wein terutama digunakan untuk menemukan frequency value kisaran AF.