Jembatan DC
DC bridgesdapat dioperasikan hanya dengan sinyal tegangan DC. Jembatan DC berguna untuk mengukur nilai hambatan yang tidak diketahui, yang ada di jembatan. Jembatan Wheatstone adalah contoh jembatan DC.
Sekarang, mari kita bahas Wheatstone’s Bridge untuk menemukan nilai resistansi yang tidak diketahui.
Jembatan Wheatstone
Jembatan Wheatstone adalah jembatan DC sederhana, yang sebagian besar memiliki empat lengan. Keempat lengan ini membentuk belah ketupat atau persegi dan masing-masing lengan terdiri dari satu resistor.
Untuk mengetahui nilai resistansi yang belum diketahui, diperlukan galvanometer dan sumber tegangan DC. Oleh karena itu, salah satu dari keduanya ditempatkan di satu diagonal jembatan Wheatstone dan yang lainnya ditempatkan di diagonal lain jembatan Wheatstone.
Jembatan Wheatstone digunakan untuk mengukur nilai hambatan sedang. Itucircuit diagram Jembatan Wheatstone ditunjukkan pada gambar di bawah ini.
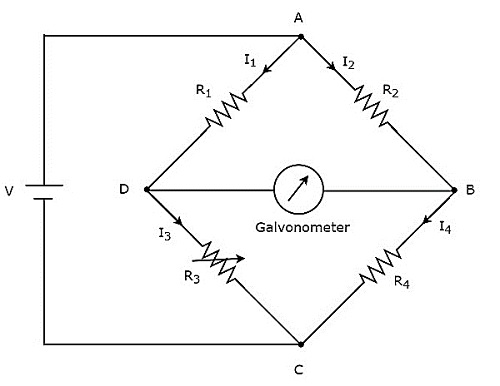
Di sirkuit di atas, lengan AB, BC, CD dan DA bersama-sama membentuk a rhombusatau bentuk persegi. Mereka terdiri dari resistor $ R_ {2} $, $ R_ {4} $, $ R_ {3} $ dan $ R_ {1} $. Biarkan arus yang mengalir melalui lengan resistor ini masing-masing adalah $ I_ {2} $, $ I_ {4} $, $ I_ {3} $ dan $ I_ {1} $ dan arah arus ini ditunjukkan pada gambar.
Lengan diagonal DB dan AC terdiri dari sumber tegangan galvanometer dan DC masing-masing V volt. Di sini, resistor, $ R_ {3} $ adalah resistor variabel standar dan resistor, $ R_ {4} $ adalah resistor yang tidak diketahui. Kita dapatbalance the bridge, dengan memvariasikan nilai resistansi resistor, $ R_ {3} $.
Rangkaian jembatan di atas seimbang ketika tidak ada arus yang mengalir melalui lengan diagonal, DB. Artinya, adano deflection di galvanometer, saat jembatan seimbang.
Jembatan itu akan seimbang, bila berikut ini two conditions puas.
Tegangan di lengan AD sama dengan tegangan di lengan AB. yaitu,
$$ V_ {AD} = V_ {AB} $$
$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $ Persamaan 1
Tegangan di lengan DC sama dengan tegangan di lengan BC. yaitu,
$$ V_ {DC} = V_ {BC} $$
$ \ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4} $ Persamaan 2
Dari dua kondisi keseimbangan di atas, kita akan mendapatkan yang berikut ini two conclusions.
Arus yang mengalir melalui lengan AD akan sama dengan arus yang mengalir melalui lengan DC. yaitu,
$$ I_ {1} = I_ {3} $$
Arus yang mengalir melalui lengan AB akan sama dengan arus yang mengalir melalui lengan BC. yaitu,
$$ I_ {2} = I_ {4} $$
Ambil rasio Persamaan 1 dan Persamaan 2.
$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $ Persamaan 3
Pengganti, $ I_ {1} = I_ {3} $ dan $ I_ {2} = I_ {4} $ pada Persamaan 3.
$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$
$$ \ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$
$$ \ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
Dengan mengganti nilai resistor yang diketahui $ R_ {1} $, $ R_ {2} $ dan $ R_ {3} $ dalam persamaan di atas, kita akan mendapatkan value of resistor,$R_{4}$.