Sosok Lissajous
Lissajous figureadalah pola yang ditampilkan di layar, ketika sinyal sinusoidal diterapkan ke pelat defleksi horizontal & vertikal CRO. Pola ini akan bervariasi berdasarkan amplitudo, frekuensi, dan perbedaan fasa dari sinyal sinusoidal, yang diterapkan pada pelat defleksi horizontal & vertikal CRO.
Gambar berikut menunjukkan example sosok Lissajous.
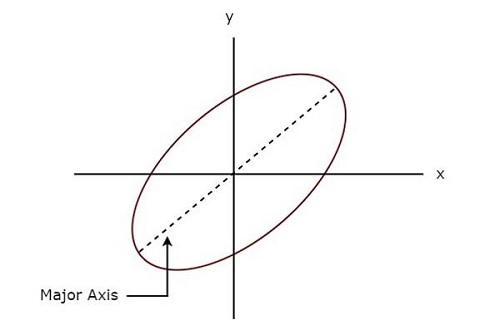
Sosok Lissajous di atas ada elliptical shape dan sumbu utamanya memiliki beberapa sudut kemiringan dengan sumbu x positif.
Pengukuran menggunakan Angka Lissajous
Kami dapat melakukan hal berikut two measurements dari sosok Lissajous.
- Frekuensi sinyal sinusoidal
- Perbedaan fasa antara dua sinyal sinusoidal
Sekarang, mari kita bahas tentang kedua pengukuran ini satu per satu.
Pengukuran Frekuensi
Sosok lissajous akan ditampilkan di layar, ketika sinyal sinusoidal diterapkan ke pelat defleksi horizontal & vertikal CRO. Oleh karena itu, terapkan sinyal sinusoidal yang memiliki standarknown frequencyke pelat defleksi horizontal CRO. Demikian pula, terapkan sinyal sinusoidal, yangfrequency adalah unknown ke pelat defleksi vertikal CRO
Misalkan, $ f_ {H} $ dan $ f_ {V} $ adalah frekuensi sinyal sinusoidal, yang masing-masing diterapkan pada pelat defleksi horizontal & vertikal CRO. Hubungan antara $ f_ {H} $ dan $ f_ {V} $ bisa jadimathematically direpresentasikan seperti di bawah ini.
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
Dari hubungan di atas, kita akan mendapatkan frekuensi sinyal sinusoidal, yang diterapkan pada pelat defleksi vertikal CRO sebagai
$ f_ {V} = \ kiri (\ frac {n_ {H}} {n_ {V}} \ kanan) f_ {H} $ (Persamaan 1)
Dimana,
$ n_ {H} $ adalah jumlah garis singgung horizontal
$ n_ {V} $ adalah jumlah garis singgung vertikal
Kita dapat menemukan nilai $ n_ {H} $ dan $ n_ {V} $ dari figur Lissajous. Jadi, dengan mengganti nilai $ n_ {H} $, $ n_ {V} $ dan $ f_ {H} $ pada Persamaan 1, kita akan mendapatkan nilai$f_{V}$, yaitu frequency of sinusoidal signal yang diterapkan pada pelat defleksi vertikal CRO.
Pengukuran Perbedaan Fase
Sosok Lissajous ditampilkan di layar ketika sinyal sinusoidal diterapkan ke pelat defleksi horizontal & vertikal CRO. Oleh karena itu, terapkan sinyal sinusoidal, yang memilikisame amplitude and frequency ke pelat defleksi horizontal dan vertikal CRO.
Untuk beberapa figur Lissajous berdasarkan bentuknya, kita dapat langsung mengetahui perbedaan fasa antara dua sinyal sinusoidal.
Jika sosok Lissajous adalah a straight line dengan kemiringan $ 45 ^ {\ circ} $ dengan sumbu x positif, maka phase differenceantara dua sinyal sinusoidal akan menjadi $ 0 ^ {\ circ} $. Artinya, tidak ada perbedaan fasa antara kedua sinyal sinusoidal tersebut.
Jika sosok Lissajous adalah a straight line dengan kemiringan $ 135 ^ {\ circ} $ dengan sumbu x positif, maka phase differenceantara dua sinyal sinusoidal akan menjadi $ 180 ^ {\ circ} $. Artinya, kedua sinyal sinusoidal tersebut berada di luar fase.
Jika sosok Lissajous masuk circular shape, maka perbedaan fase antara dua sinyal sinusoidal adalah $ 90 ^ {\ circ} $ atau $ 270 ^ {\ circ} $.
Kita dapat menghitung perbedaan fasa antara dua sinyal sinusoidal dengan menggunakan rumus, jika angka Lissajous adalah elliptical shape.
Jika sumbu utama dari bentuk elips Sosok Lissajous yang memiliki sudut kemiringan terletak antara $ 0 ^ {\ circ} $ dan $ 90 ^ {\ circ} $ dengan sumbu x positif, maka perbedaan fasa antara kedua sinyal sinusoidal adalah.
$$ \ phi = \ sin ^ {- 1} \ kiri (\ frac {x_ {1}} {x_ {2}} \ kanan) = \ sin ^ {- 1} \ kiri (\ frac {y_ {1} } {y_ {2}} \ kanan) $$
Jika sumbu utama dari bentuk elips Angka Lissajous yang memiliki sudut kemiringan terletak antara $ 90 ^ {\ circ} $ dan $ 180 ^ {\ circ} $ dengan sumbu x positif, maka perbedaan fase antara kedua sinyal sinusoidal adalah.
$$ \ phi = 180 - \ sin ^ {- 1} \ kiri (\ frac {x_ {1}} {x_ {2}} \ kanan) = 180 - \ sin ^ {- 1} \ kiri (\ frac { y_ {1}} {y_ {2}} \ kanan) $$
Where,
$ x_ {1} $ adalah jarak dari titik asal ke titik pada sumbu x, tempat perpotongan angka Lissajous berbentuk elips
$ x_ {2} $ adalah jarak dari titik asal ke garis singgung vertikal bentuk elips Angka Lissajous
$ y_ {1} $ adalah jarak dari titik asal ke titik pada sumbu y, di mana bentuk elips berpotongan dengan sosok Lissajous
$ y_ {2} $ adalah jarak dari titik asal ke garis singgung horizontal bentuk elips Angka Lissajous
Pada bab ini, kami akan mempelajari cara mencari frekuensi sinyal sinusoidal yang tidak diketahui dan perbedaan fasa antara dua sinyal sinusoidal dari gambar Lissajous dengan menggunakan rumus.