SymPy - Panduan Cepat
SymPy adalah pustaka Python untuk melakukan komputasi simbolik. Ini adalah sebuahcomputer algebra system(CAS) yang dapat digunakan baik sebagai aplikasi mandiri, sebagai pustaka untuk aplikasi lain. Sesi live-nya juga tersedia dihttps://live.sympy.org/. Karena ini adalah pustaka Python murni, ini dapat digunakan sebagai mode interaktif dan sebagai aplikasi terprogram. SymPy sekarang telah menjadi pustaka simbolik populer untuk ekosistem Python ilmiah.
SymPy memiliki berbagai fitur yang dapat diterapkan di bidang aritmatika simbolik dasar, kalkulus, aljabar, matematika diskrit, fisika kuantum, dll. SymPy mampu memformat hasil dalam berbagai format termasuk LaTeX, MathML, dll. SymPy didistribusikan di bawah Lisensi BSD Baru. Sebuah tim pengembang yang dipimpin olehOndřej Čertík dan Aaron Meurer menerbitkan versi pertama SymPy pada tahun 2007. Versi saat ini adalah 1.5.1.
Beberapa area aplikasi SymPy adalah -
- Polynomials
- Calculus
- Matematika diskrit
- Matrices
- Geometry
- Plotting
- Physics
- Statistics
- Combinatorics
SymPy memiliki satu pustaka prasyarat penting bernama mpmath. Ini adalah pustaka Python untuk aritmatika floating-point nyata dan kompleks dengan presisi yang sewenang-wenang. Namun, PIP penginstal paket Python menginstalnya secara otomatis ketika SymPy diinstal sebagai berikut -
pip install sympyDistribusi Python lain seperti Anaconda, Enthought Canopy, dll., Mungkin memiliki SymPy yang sudah digabungkan di dalamnya. Untuk memverifikasi, Anda dapat mengetik berikut ini di prompt Python -
>>> import sympy
>>> sympy.__version__Dan Anda mendapatkan output di bawah ini sebagai versi sympy saat ini -
'1.5.1'
Kode sumber paket SymPy tersedia di https://github.com/sympy/sympy.
Perhitungan simbolik mengacu pada pengembangan algoritma untuk memanipulasi ekspresi matematika dan objek matematika lainnya. Komputasi simbolik mengintegrasikan matematika dengan ilmu komputer untuk menyelesaikan ekspresi matematika menggunakan simbol matematika. Sistem Aljabar Komputer (CAS) seperti SymPy mengevaluasi ekspresi aljabar secara tepat (bukan perkiraan) menggunakan simbol yang sama yang digunakan dalam metode manual tradisional. Misalnya, kami menghitung akar kuadrat dari sebuah angka menggunakan modul matematika Python seperti yang diberikan di bawah ini -
>>> import math
>>> print (math.sqrt(25), math.sqrt(7))Output dari potongan kode di atas adalah sebagai berikut -
5.0 2.6457513110645907
Seperti yang Anda lihat, akar kuadrat dari 7 dihitung kira-kira. Tetapi dalam akar kuadrat SymPy dari angka-angka yang bukan kuadrat sempurna dibiarkan tidak dievaluasi secara default seperti yang diberikan di bawah ini -
>>> import sympy
>>> print (sympy.sqrt(7))Output dari potongan kode di atas adalah sebagai berikut -
sqrt(7)
Dimungkinkan untuk menyederhanakan dan menampilkan hasil ekspresi secara simbolis dengan potongan kode di bawah ini -
>>> import math
>>> print (math.sqrt(12))Output dari potongan kode di atas adalah sebagai berikut -
3.4641016151377544
Anda perlu menggunakan potongan kode di bawah ini untuk menjalankan hal yang sama menggunakan sympy -
##sympy output
>>> print (sympy.sqrt(12))Dan outputnya adalah sebagai berikut -
2*sqrt(3)
Kode SymPy, saat dijalankan di notebook Jupyter, menggunakan pustaka MathJax untuk merender simbol matematika dalam bentuk LatEx. Ini ditunjukkan pada potongan kode di bawah ini -
>>> from sympy import *
>>> x=Symbol ('x')
>>> expr = integrate(x**x, x)
>>> exprSaat menjalankan perintah di atas dalam shell python, output berikut akan dihasilkan -
Integral(x**x, x)Yang mana setara dengan
$\int \mathrm{x}^{x}\,\mathrm{d}x$
Akar kuadrat dari kuadrat tidak sempurna dapat diwakili oleh Lateks sebagai berikut menggunakan simbol tradisional -
>>> from sympy import *
>>> x=7
>>> sqrt(x)Output dari potongan kode di atas adalah sebagai berikut -
$\sqrt7$
Sistem komputasi simbolik seperti SymPy melakukan semua jenis komputasi (seperti turunan, integral, dan batas, menyelesaikan persamaan, bekerja dengan matriks) secara simbolis. Paket SymPy memiliki modul berbeda yang mendukung plotting, pencetakan (seperti LATEX), fisika, statistik, kombinatorik, teori bilangan, geometri, logika, dll.
Modul inti dalam paket SymPy berisi kelas Nomor yang mewakili nomor atom. Kelas ini memiliki dua subclass: kelas Float dan Rational. Kelas rasional selanjutnya diperluas dengan kelas Integer.
Kelas float merepresentasikan jumlah floating point presisi arbitrer.
>>> from sympy import Float
>>> Float(6.32)Output dari potongan kode di atas adalah sebagai berikut -
6.32
SymPy dapat mengubah integer atau string menjadi float.
>>> Float(10)10.0
Float('1.33E5')# scientific notation133000.0
Saat mengonversi menjadi float, dimungkinkan juga untuk menentukan jumlah digit untuk presisi seperti yang diberikan di bawah ini -
>>> Float(1.33333,2)Output dari potongan kode di atas adalah sebagai berikut -
1.3
Representasi bilangan (p / q) direpresentasikan sebagai objek kelas Rasional dengan q sebagai bilangan bukan nol.
>>> Rational(3/4)Output dari potongan kode di atas adalah sebagai berikut -
$\frac{3}{4}$
Jika bilangan floating point diteruskan ke konstruktor Rational (), ia mengembalikan nilai yang mendasari representasi binernya
>>> Rational(0.2)Output dari potongan kode di atas adalah sebagai berikut -
$\frac{3602879701896397}{18014398509481984}$
Untuk representasi yang lebih sederhana, tentukan batasan penyebut.
>>> Rational(0.2).limit_denominator(100)Output dari potongan kode di atas adalah sebagai berikut -
$\frac{1}{5}$
Saat string diteruskan ke konstruktor Rational (), sejumlah rasional presisi arbitrer dikembalikan.
>>> Rational("3.65")Output dari potongan kode di atas adalah sebagai berikut -
$\frac{73}{20}$
Objek rasional juga dapat diperoleh jika dua argumen angka dilewatkan. Bagian pembilang dan penyebut tersedia sebagai properti.
>>> a=Rational(3,5)
>>> print (a)
>>> print ("numerator:{}, denominator:{}".format(a.p, a.q))Output dari potongan kode di atas adalah sebagai berikut -
3/5
numerator:3, denominator:5
>>> aOutput dari potongan kode di atas adalah sebagai berikut -
$\frac{3}{5}$
Kelas integer di SymPy mewakili bilangan bulat dengan ukuran berapa pun. Konstruktor dapat menerima bilangan Float atau Rasional, tetapi bagian pecahannya dibuang
>>> Integer(10)Output dari potongan kode di atas adalah sebagai berikut -
10
>>> Integer(3.4)Output dari potongan kode di atas adalah sebagai berikut -
3
>>> Integer(2/7)Output dari potongan kode di atas adalah sebagai berikut -
0
SymPy memiliki file RealNumberkelas yang bertindak sebagai alias untuk Float. SymPy juga mendefinisikan Zero dan One sebagai kelas tunggal yang masing-masing dapat diakses dengan S.Zero dan S.One seperti yang ditunjukkan di bawah ini -
>>> S.ZeroOutputnya adalah sebagai berikut -
0
>>> S.OneOutputnya adalah sebagai berikut -
1
Objek nomor Singleton standar lainnya adalah Half, NaN, Infinity dan ImaginaryUnit
>>> from sympy import S
>>> print (S.Half)Outputnya adalah sebagai berikut -
½
>>> print (S.NaN)Outputnya adalah sebagai berikut -
nan
Infinity tersedia sebagai objek simbol oo atau S.Infinity
>>> from sympy import oo
>>> ooOutput dari potongan kode di atas adalah sebagai berikut -
$\infty$
>>> S.InfinityOutput dari potongan kode di atas adalah sebagai berikut -
$\infty$
Nomor ImaginaryUnit dapat diimpor sebagai simbol I atau diakses sebagai S. ImaginaryUnit dan mewakili akar kuadrat -1
>>> from sympy import I
>>> ISaat Anda menjalankan cuplikan kode di atas, Anda mendapatkan output berikut -
i
>>> S.ImaginaryUnitOutput dari potongan di atas adalah sebagai berikut -
i
>>> from sympy import sqrt
>>> i=sqrt(-1)
>>> i*iSaat Anda menjalankan cuplikan kode di atas, Anda mendapatkan output berikut -
-1
Symboladalah kelas paling penting di perpustakaan symPy. Seperti disebutkan sebelumnya, perhitungan simbolik dilakukan dengan simbol. Variabel SymPy adalah objek dari kelas Symbols.
Argumen fungsi Symbol () adalah string yang berisi simbol yang dapat ditempatkan ke variabel.
>>> from sympy import Symbol
>>> x=Symbol('x')
>>> y=Symbol('y')
>>> expr=x**2+y**2
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^2 + y^2$
Sebuah simbol bisa lebih dari satu huruf.
>>> s=Symbol('side')
>>> s**3Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$side^3$
SymPy juga memiliki file Symbols()fungsi yang dapat mendefinisikan banyak simbol sekaligus. String berisi nama variabel yang dipisahkan dengan koma atau spasi.
>>> from sympy import symbols
>>> x,y,z=symbols("x,y,z")Dalam modul abc SymPy, semua huruf Latin dan Yunani didefinisikan sebagai simbol. Karenanya, alih-alih membuat instance objek Simbol, metode ini lebih mudah.
>>> from sympy.abc import x,y,zNamun, namanya C, O, S, I, N, E dan Qadalah simbol yang telah ditentukan sebelumnya. Selain itu, simbol dengan lebih dari satu huruf tidak ditentukan dalam modul abc, di mana Anda harus menggunakan objek Simbol seperti di atas. Modul abc mendefinisikan nama khusus yang dapat mendeteksi definisi di namespace SymPy default. clash1 berisi satu huruf dan clash2 memiliki simbol bentrok multi huruf
>>> from sympy.abc import _clash1, _clash2
>>> _clash1Output dari potongan di atas adalah sebagai berikut -
{'C': C, 'O': O, 'Q': Q, 'N': N, 'I': I, 'E': E, 'S': S}
>>> _clash2Output dari potongan di atas adalah sebagai berikut -
{'beta': beta, 'zeta': zeta, 'gamma': gamma, 'pi': pi}
Simbol yang diindeks dapat didefinisikan menggunakan sintaks yang mirip dengan fungsi range (). Rentang ditunjukkan oleh titik dua. Jenis rentang ditentukan oleh karakter di sebelah kanan titik dua. Jika itr adalah sebuah digit, semua digit yang bersebelahan ke kiri diambil sebagai nilai awal nonnegatif. Semua angka yang berdekatan di sebelah kanan diambil 1 lebih besar dari nilai akhir.
>>> from sympy import symbols
>>> symbols('a:5')Output dari potongan di atas adalah sebagai berikut -
(a0, a1, a2, a3, a4)
>>> symbols('mark(1:4)')Output dari potongan di atas adalah sebagai berikut -
(mark1, mark2, mark3)
Salah satu operasi paling dasar yang harus dilakukan pada ekspresi matematika adalah substitusi. Fungsi subs () di SymPy menggantikan semua kemunculan parameter pertama dengan yang kedua.
>>> from sympy.abc import x,a
>>> expr=sin(x)*sin(x)+cos(x)*cos(x)
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\sin^2(x)+\cos^2(x)$
>>> expr.subs(x,a)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\sin^2(a)+\cos^2(a)$
Fungsi ini berguna jika kita ingin mengevaluasi ekspresi tertentu. Misalnya, kami ingin menghitung nilai ekspresi berikut dengan mengganti a dengan 5.
>>> expr=a*a+2*a+5
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$a^2 + 2a + 5$
expr.subs(a,5)Potongan kode di atas memberikan output berikut -
40
>>> from sympy.abc import x
>>> from sympy import sin, pi
>>> expr=sin(x)
>>> expr1=expr.subs(x,pi)
>>> expr1Potongan kode di atas memberikan output berikut -
0
Fungsi ini juga digunakan untuk mengganti subekspresi dengan subekspresi lain. Dalam contoh berikut, b diganti dengan a + b.
>>> from sympy.abc import a,b
>>> expr=(a+b)**2
>>> expr1=expr.subs(b,a+b)
>>> expr1Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$(2a + b)^2$
Fungsi sympify () digunakan untuk mengonversi ekspresi sembarang apa pun sehingga dapat digunakan sebagai ekspresi SymPy. Objek Python normal seperti objek integer diubah dalam SymPy. Integer, dll .., string juga diubah menjadi ekspresi SymPy.
>>> expr="x**2+3*x+2"
>>> expr1=sympify(expr)
>>> expr1
>>> expr1.subs(x,2)Potongan kode di atas memberikan output berikut -
12
Objek Python apa pun dapat diubah dalam objek SymPy. Namun, karena konversi secara internal menggunakan fungsi eval (), ekspresi unsanitized tidak boleh digunakan, jika tidak SympifyError dimunculkan.
>>> sympify("x***2")
---------------------------------------------------------------------------SympifyError: Sympify of expression 'can't parse' x *** 2 '' gagal, karena pengecualian dimunculkan.
Fungsi sympify () mengambil argumen berikut: * strict: default is False. Jika disetel ke True, hanya jenis yang konversi eksplisitnya telah ditentukan yang dikonversi. Jika tidak, SympifyError akan dimunculkan. * evaluasi: Jika disetel ke False, aritmatika dan operator akan diubah menjadi padanan SymPy mereka tanpa mengevaluasi ekspresi.
>>> sympify("10/5+4/2")Potongan kode di atas memberikan output berikut -
4
>>> sympify("10/5+4/2", evaluate=False)Potongan kode di atas memberikan output berikut -
$\frac{10}{5}+\frac{4}{2}$
Fungsi ini mengevaluasi ekspresi numerik tertentu hingga presisi floating point tertentu hingga 100 digit. Fungsi ini juga mengambil sub parameter objek kamus dari nilai numerik untuk simbol. Pertimbangkan ekspresi berikut
>>> from sympy.abc import r
>>> expr=pi*r**2
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\Pi{r^2}$
Untuk mengevaluasi ekspresi di atas menggunakan fungsi evalf () dengan mengganti r dengan 5
>>> expr.evalf(subs={r:5})Potongan kode di atas memberikan output berikut -
78.5398163397448
Secara default, presisi floating point adalah hingga 15 digit yang dapat diganti dengan angka apapun hingga 100. Ekspresi berikut dievaluasi hingga presisi 20 digit.
>>> expr=a/b
>>> expr.evalf(20, subs={a:100, b:3})Potongan kode di atas memberikan output berikut -
33.333333333333333333
Fungsi lambdify menerjemahkan ekspresi SymPy menjadi fungsi Python. Jika ekspresi akan dievaluasi pada rentang nilai yang besar, fungsi evalf () tidak efisien. lambdify bertindak seperti fungsi lambda, kecuali itu mengubah nama SymPy menjadi nama perpustakaan numerik yang diberikan, biasanya NumPy. Secara default, lambdify pada implementasi di pustaka standar matematika.
>>> expr=1/sin(x)
>>> f=lambdify(x, expr)
>>> f(3.14)Potongan kode di atas memberikan output berikut -
627.8831939138764
Ekspresi tersebut mungkin memiliki lebih dari satu variabel. Dalam kasus tersebut, argumen pertama ke fungsi lambdify () adalah daftar variabel, diikuti dengan ekspresi yang akan dievaluasi.
>>> expr=a**2+b**2
>>> f=lambdify([a,b],expr)
>>> f(2,3)Potongan kode di atas memberikan output berikut -
13
Namun, untuk memanfaatkan pustaka numpy sebagai backend numerik, kita harus mendefinisikan yang sama sebagai argumen untuk fungsi lambdify ().
>>> f=lambdify([a,b],expr, "numpy")Kami menggunakan dua array numpy untuk dua argumen a dan b dalam fungsi di atas. Waktu eksekusi sangat cepat jika ada array numpy.
>>> import numpy
>>> l1=numpy.arange(1,6)
>>> l2=numpy.arange(6,11)
>>> f(l1,l2)Potongan kode di atas memberikan output berikut -
array([ 37, 53, 73, 97, 125], dtype=int32)
Fungsi Boolean didefinisikan dalam sympy.basic.booleanarg module. Dimungkinkan untuk membangun ekspresi Boolean dengan operator python standar & (And), | (Atau), ~ (Not) serta dengan >> dan <<. Ekspresi Boolean mewarisi dari kelas Basic yang didefinisikan dalam modul inti SymPy.
Fungsi BooleanTrue
Fungsi ini setara dengan True seperti pada inti Python. Ini mengembalikan singleton yang bisa diambil oleh S.true.
>>> from sympy import *
>>> x=sympify(true)
>>> x, S.truePotongan kode di atas memberikan output berikut -
(Betul betul)
Fungsi BooleanFalse
Demikian pula, fungsi ini setara dengan Boolean False di Python dan dapat diakses oleh S.false
>>> from sympy import *
>>> x=sympify(false)
>>> x, S.falsePotongan kode di atas memberikan output berikut -
(Salah, Salah)
Dan fungsinya
Fungsi logika AND mengevaluasi dua argumennya dan mengembalikan False jika salah satunya adalah False. Fungsi mengemulasi & operator.
>>> from sympy import *
>>> from sympy.logic.boolalg import And
>>> x,y=symbols('x y')
>>> x=True
>>> y=True
>>> And(x,y), x"&"yPotongan kode di atas memberikan output berikut -
(Betul betul)
>>> y=False
>>> And(x,y), x"&"yPotongan kode di atas memberikan output berikut -
(Salah, Salah)
Atau fungsi
Fungsi ini mengevaluasi dua argumen Boolean dan mengembalikan True jika salah satunya adalah True. The | operator dengan mudah meniru perilakunya.
>>> from sympy import *
>>> from sympy.logic.boolalg import Or
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Or(x,y), x|yPotongan kode di atas memberikan output berikut -
(Betul betul)
>>> x=False
>>> y=False
>>> Or(x,y), x|yPotongan kode di atas memberikan output berikut -
(Salah, Salah)
Tidak berfungsi
Fungsi Logical Not menghasilkan negasi dari argumen Boolean. Ia mengembalikan True jika argumennya False dan mengembalikan False jika True. Operator ~ melakukan operasi yang mirip dengan Not function. Itu ditunjukkan pada contoh di bawah ini -
>>> from sympy import *
>>> from sympy.logic.boolalg import Or, And, Not
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Not(x), Not(y)Potongan kode di atas memberikan output berikut -
(Salah benar)
>>> Not(And(x,y)), Not(Or(x,y))Potongan kode di atas memberikan output berikut -
(Benar salah)
Fungsi Xor
Fungsi Logical XOR (eksklusif OR) mengembalikan True jika bilangan ganjil dari argumen adalah True dan sisanya adalah False dan mengembalikan False jika bilangan genap dari argumen adalah Benar dan sisanya adalah False. Operasi serupa dilakukan oleh operator ^.
>>> from sympy import *
>>> from sympy.logic.boolalg import Xor
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Xor(x,y), x^yPotongan kode di atas memberikan output berikut -
(Betul betul)
>>> a,b,c,d,e=symbols('a b c d e')
>>> a,b,c,d,e=(True, False, True, True, False)
>>> Xor(a,b,c,d,e)Potongan kode di atas memberikan output berikut -
Benar
Dalam kasus di atas, tiga argumen (angka ganjil) adalah True, maka Xor mengembalikan true. Namun, jika jumlah argumen True genap, itu menghasilkan Salah, seperti yang ditunjukkan di bawah ini -
>>> a,b,c,d,e=(True, False, False, True, False)
>>> Xor(a,b,c,d,e)Potongan kode di atas memberikan output berikut -
Salah
Fungsi Nand
Fungsi ini menjalankan operasi Logical NAND. Ini mengevaluasi argumennya dan mengembalikan True jika ada di antaranya Salah, dan Salah jika semuanya Benar.
>>> from sympy import *
>>> from sympy.logic.boolalg import Nand
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Nand(a,b,c), Nand(a,c)Potongan kode di atas memberikan output berikut -
(Benar salah)
Atau Fungsi
Fungsi ini menjalankan operasi Logical NOR. Ini mengevaluasi argumennya dan mengembalikan False jika ada yang Benar, dan Benar jika semuanya Salah.
>>> from sympy import *
>>> from sympy.logic.boolalg import Nor
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Nor(a,b,c), Nor(a,c)Potongan kode di atas memberikan output berikut -
(Salah, Salah)
Perhatikan bahwa meskipun SymPy menyediakan operator ^ untuk Xor, ~ untuk Not, | untuk Or dan & untuk And berfungsi sebagai kenyamanan, penggunaan normalnya di Python adalah sebagai operator bitwise. Oleh karena itu, jika operan adalah bilangan bulat, hasilnya akan berbeda.
Fungsi yang setara
Fungsi ini mengembalikan relasi ekivalen. Ekuivalen (A, B) adalah True jika dan hanya jika A dan B keduanya Benar atau keduanya Salah. Fungsi mengembalikan True jika semua argumen secara logis setara. Mengembalikan False sebaliknya.
>>> from sympy import *
>>> from sympy.logic.boolalg import Equivalent
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Equivalent(a,b), Equivalent(a,c)Potongan kode di atas memberikan output berikut -
(Salah benar)
Fungsi ITE
Fungsi ini bertindak sebagai klausa If then else dalam bahasa pemrograman. TITIK (A, B, C) mengevaluasi dan mengembalikan hasil dari B jika A benar, jika tidak ia mengembalikan hasil C. Semua argumen harus berupa Boolean.
>>> from sympy import * >>> from sympy.logic.boolalg import ITE >>> a,b,c=symbols('a b c') >>> a,b,c=(True, False, True)
>>> ITE(a,b,c), ITE(a,c,b)Potongan kode di atas memberikan output berikut -
(Salah benar)
Modul asumsi dalam paket SymPy berisi alat untuk mengekstrak informasi tentang ekspresi. Modul ini mendefinisikan fungsi ask () untuk tujuan ini.
sympy.assumptions.ask(property)Properti berikut memberikan informasi yang berguna tentang ekspresi -
algebraic(x)
Untuk menjadi aljabar, angka harus merupakan akar dari persamaan polinomial bukan nol dengan koefisien rasional. √2 karena √2 adalah solusi dari x2 - 2 = 0, jadi aljabar.
complex(x)
Predikat bilangan kompleks. Benar jika dan hanya jika x termasuk dalam himpunan bilangan kompleks.
composite(x)
Predikat bilangan komposit yang dikembalikan oleh ask (Q.composite (x)) bernilai benar jika dan hanya jika x adalah bilangan bulat positif dan memiliki setidaknya satu pembagi positif selain 1 dan bilangan itu sendiri.
even, odd
Ask () mengembalikan true dari x dalam himpunan bilangan genap dan himpunan bilangan ganjil masing-masing.
imaginary
Properti ini mewakili predikat bilangan imajiner. Memang benar jika x dapat ditulis sebagai bilangan real dikalikan dengan unit imajiner I.
integer
Properti ini dikembalikan oleh Q. integer (x) mengembalikan nilai benar dari x milik kumpulan bilangan genap.
rational, irrational
Q.irasional (x) adalah benar jika dan hanya jika x adalah bilangan real apa pun yang tidak dapat dinyatakan sebagai rasio bilangan bulat. Misalnya, pi adalah bilangan irasional.
positive, negative
Predikat untuk memeriksa apakah angka itu positif atau negatif
zero, nonzero
Predikat untuk memeriksa apakah suatu angka nol atau tidak
>>> from sympy import *
>>> x=Symbol('x')
>>> x=10
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)
>>> x,y=symbols("x y")
>>> x,y=5,10
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(False, True)
>>> x,y= 2*I, 4+5*I
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> x,y=5,10
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)
>>> x,y=5,-5
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)Sympy memiliki kemampuan yang kuat untuk menyederhanakan ekspresi matematika. Ada banyak fungsi di SymPy untuk melakukan berbagai macam penyederhanaan. Fungsi umum yang disebut simplify () ada yang mencoba untuk sampai pada bentuk ekspresi yang paling sederhana.
menyederhanakan
Fungsi ini didefinisikan dalam modul sympy.simplify. simplify () mencoba menerapkan heuristik cerdas untuk membuat ekspresi input "lebih sederhana". Kode berikut menunjukkan menyederhanakan ekspresi$sin^2(x)+cos^2(x)$.
>>> from sympy import *
>>> x=Symbol('x')
>>> expr=sin(x)**2 + cos(x)**2
>>> simplify(expr)Potongan kode di atas memberikan output berikut -
1
memperluas
Expand () adalah salah satu fungsi penyederhanaan yang paling umum di SymPy, digunakan dalam memperluas ekspresi polinomial. Misalnya -
>>> a,b=symbols('a b')
>>> expand((a+b)**2)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$a^2 + 2ab + b^2$
>>> expand((a+b)*(a-b))Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$a^2 - b^2$
Fungsi expand () membuat ekspresi lebih besar, bukan lebih kecil. Biasanya demikian, tetapi sering kali ekspresi akan menjadi lebih kecil saat memanggil expand () padanya.
>>> expand((x + 1)*(x - 2) - (x - 1)*x)Potongan kode di atas memberikan output berikut -
-2
faktor
Fungsi ini mengambil polinomial dan memfaktorkannya menjadi faktor tak tersederhanakan di atas bilangan rasional.
>>> x,y,z=symbols('x y z')
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor(expr)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$z(x + 2y)^2$
>>> factor(x**2+2*x+1)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$(x + 1)^2$
Fungsi faktor () adalah kebalikan dari expand (). Setiap faktor yang dikembalikan oleh faktor () dijamin tidak dapat direduksi. Fungsi factor_list () mengembalikan keluaran yang lebih terstruktur.
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor_list(expr)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
(1, [(z, 1), (x + 2*y, 2)])
mengumpulkan
Fungsi ini mengumpulkan istilah tambahan dari suatu ekspresi sehubungan dengan daftar ekspresi hingga pangkat dengan eksponen rasional.
>>> expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^3 + x^2z + 2x^2 + xy + x - 3$
Fungsi collect () pada ekspresi ini menghasilkan sebagai berikut -
>>> collect(expr,x)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^3 + x^2(2 - z) + x(y + 1) - 3$
>>> expr=y**2*x + 4*x*y*z + 4*y**2*z+y**3+2*x*y
>>> collect(expr,y)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$Y^3+Y^2(x+4z)+y(4xz+2x)$
membatalkan
Fungsi cancel () akan menggunakan fungsi rasional dan memasukkannya ke dalam bentuk kanonik standar, p / q, di mana p dan q adalah polinomial yang diperluas tanpa faktor persekutuan. Koefisien utama p dan q tidak memiliki penyebut, yaitu bilangan bulat.
>>> expr1=x**2+2*x+1
>>> expr2=x+1
>>> cancel(expr1/expr2)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x+1$
>>> expr = 1/x + (3*x/2 - 2)/(x - 4)
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{\frac{3x}{2} - 2}{x - 4} + \frac{1}{x}$
>>> cancel(expr)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{3x^2 - 2x - 8}{2x^2 - 8}$
>>> expr=1/sin(x)**2
>>> expr1=sin(x)
>>> cancel(expr1*expr)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{1}{\sin(x)}$
trigsimp
Fungsi ini digunakan untuk menyederhanakan identitas trigonometri. Perlu diperhatikan bahwa konvensi penamaan untuk fungsi trigonometri terbalik adalah dengan menambahkan a di depan nama fungsi. Misalnya, invers cosinus, atau arc cosine, disebut acos ().
>>> from sympy import trigsimp, sin, cos
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2
>>> trigsimp(expr)2
Fungsi trigsimp menggunakan heuristik untuk menerapkan identitas trigonometri yang paling sesuai.
PowerSimp
Fungsi ini mengurangi ekspresi yang diberikan dengan menggabungkan pangkat dengan basis dan eksponen yang serupa.
>>> expr=x**y*x**z*y**z
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^y x^z y^z$
>>> powsimp(expr)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^{y+z} y^z$
Anda dapat membuat powsimp () hanya menggabungkan basa atau hanya menggabungkan eksponen dengan mengubah gabung = 'basis' atau gabung = 'exp'. Secara default, gabungkan = 'semua', yang melakukan keduanya. Jika gaya True maka basis akan digabungkan tanpa memeriksa asumsi.
>>> powsimp(expr, combine='base', force=True)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^y(xy)^z$
combsimp
Ekspresi kombinatorial yang melibatkan faktorial dan binomial dapat disederhanakan dengan menggunakan fungsi combsimp (). SymPy menyediakan fungsi faktorial ()
>>> expr=factorial(x)/factorial(x - 3)
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{x!}{(x - 3)!}$
Untuk menyederhanakan ekspresi kombinatorial di atas kita menggunakan fungsi combsimp () sebagai berikut -
>>> combsimp(expr)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x(x-2)(x-1)$
Binomial (x, y) adalah banyaknya cara untuk memilih y item dari sekumpulan x item yang berbeda. Itu juga sering ditulis sebagai xCy.
>>> binomial(x,y)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$(\frac{x}{y})$
>>> combsimp(binomial(x+1, y+1)/binomial(x, y))Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{x + 1}{y + 1}$
logcombine.dll
Fungsi ini mengambil logaritma dan menggabungkannya menggunakan aturan berikut -
- log (x) + log (y) == log (x * y) jika keduanya positif
- a * log (x) == log (x ** a) jika x positif dan a nyata
>>> logcombine(a*log(x) + log(y) - log(z))Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$a\log(x) + \log(y) - \log(z)$
Jika parameter gaya dari fungsi ini disetel ke True, maka asumsi di atas akan dianggap berlaku jika tidak ada asumsi yang diterapkan pada suatu kuantitas.
>>> logcombine(a*log(x) + log(y) - log(z), force=True)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\log\frac{x^a y}{z}$
Turunan dari suatu fungsi adalah laju perubahan seketika terhadap salah satu variabelnya. Ini setara dengan mencari kemiringan garis singgung fungsi pada suatu titik. Kita dapat mencari diferensiasi ekspresi matematika dalam bentuk variabel dengan menggunakan fungsi diff () dalam paket SymPy.
diff(expr, variable)
>>> from sympy import diff, sin, exp
>>> from sympy.abc import x,y
>>> expr=x*sin(x*x)+1 >>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x\sin(x^2) + 1$
>>> diff(expr,x)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$2x^2\cos(x^2) + \sin(x^2)$
>>> diff(exp(x**2),x)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
2xex2
Untuk mengambil beberapa turunan, berikan variabel sebanyak yang ingin Anda bedakan, atau berikan angka setelah variabel.
>>> diff(x**4,x,3)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$24x$
>>> for i in range(1,4): print (diff(x**4,x,i))Potongan kode di atas memberikan ekspresi di bawah ini -
4*x**3
12*x**2
24*x
Dimungkinkan juga untuk memanggil metode diff () dari sebuah ekspresi. Ia bekerja sama seperti fungsi diff ().
>>> expr=x*sin(x*x)+1
>>> expr.diff(x)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$2x^2\cos(x^2) + \sin(x^2)$
Turunan yang tidak dievaluasi dibuat dengan menggunakan kelas Derivatif. Ini memiliki sintaks yang sama dengan fungsi diff (). Untuk mengevaluasi turunan yang tidak dievaluasi, gunakan metode doit.
>>> from sympy import Derivative
>>> d=Derivative(expr)
>>> dPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{d}{dx}(x\sin(x^2)+1)$
>>> d.doit()Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$2x^2\cos(x^2) + \sin(x^2)$
Paket SymPy berisi modul integral. Ini mengimplementasikan metode untuk menghitung integral ekspresi pasti dan tak terbatas. Metode integratif () digunakan untuk menghitung integral pasti dan tak tentu. Untuk menghitung integral tak tentu atau primitif, cukup teruskan variabel setelah ekspresi.
Misalnya -
integrate(f, x)Untuk menghitung integral tertentu, berikan argumen sebagai berikut -
(integration_variable, lower_limit, upper_limit)>>> from sympy import *
>>> x,y = symbols('x y')
>>> expr=x**2 + x + 1
>>> integrate(expr, x)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{x^3}{3} + \frac{x^2}{2} + x$
>>> expr=sin(x)*tan(x)
>>> expr
>>> integrate(expr,x)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$-\frac{\log(\sin(x) - 1)}{2} + \frac{\log(\sin(x) + 1)}{2} - \sin(x)$
Contoh integral pasti diberikan di bawah ini -
>>> expr=exp(-x**2)
>>> integrate(expr,(x,0,oo) )Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{\sqrt\pi}{2}$
Anda dapat melewatkan beberapa tupel batas untuk melakukan beberapa integral. Contoh diberikan di bawah ini -
>>> expr=exp(-x**2 - y**2)
>>> integrate(expr,(x,0,oo),(y,0,oo))Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{\pi}{4}$
Anda bisa membuat integral yang tidak dievaluasi menggunakan objek Integral, yang bisa dievaluasi dengan memanggil metode doit ().
>>> expr = Integral(log(x)**2, x)
>>> exprPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\int \mathrm\log(x)^2 \mathrm{d}x$
>>> expr.doit()Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x\log(x)^2 - 2xlog(x) + 2x$
Transformasi Integral
SymPy mendukung berbagai jenis transformasi integral sebagai berikut -
- laplace_transform
- fourier_transform
- sine_transform
- cosine_transform
- hankel_transform
Fungsi-fungsi ini didefinisikan dalam modul sympy.integrals.transforms. Contoh berikut menghitung transformasi Fourier dan transformasi Laplace masing-masing.
Example 1
>>> from sympy import fourier_transform, exp
>>> from sympy.abc import x, k
>>> expr=exp(-x**2)
>>> fourier_transform(expr, x, k)Saat menjalankan perintah di atas dalam shell python, output berikut akan dihasilkan -
sqrt(pi)*exp(-pi**2*k**2)Yang setara dengan -
$\sqrt\pi * e^{\pi^2k^2}$
Example 2
>>> from sympy.integrals import laplace_transform
>>> from sympy.abc import t, s, a
>>> laplace_transform(t**a, t, s)Saat menjalankan perintah di atas dalam shell python, output berikut akan dihasilkan -
(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)Dalam Matematika, matriks adalah larik dua dimensi dari angka, simbol, atau ekspresi. Teori manipulasi matriks berkaitan dengan melakukan operasi aritmatika pada objek matriks, tunduk pada aturan tertentu.
Transformasi linier adalah salah satu aplikasi penting dari matriks. Banyak bidang keilmuan, khususnya yang berkaitan dengan Fisika menggunakan aplikasi terkait matriks.
Paket SymPy memiliki modul matriks yang menangani penanganan matriks. Ini termasuk kelas Matrix yang objeknya mewakili matriks.
Note: If you want to execute all the snippets in this chapter individually, you need to import the matrix module as shown below −
>>> from sympy.matrices import MatrixExample
>>> from sympy.matrices import Matrix
>>> m=Matrix([[1,2,3],[2,3,1]])
>>> m
$\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 3 & 1\end{matrix}\right]$Saat menjalankan perintah di atas dalam shell python, output berikut akan dihasilkan -
[1 2 3 2 3 1]
Matriks dibuat dari objek List dengan ukuran yang sesuai. Anda juga bisa mendapatkan matriks dengan mendistribusikan item daftar dalam jumlah baris dan kolom yang ditentukan.
>>> M=Matrix(2,3,[10,40,30,2,6,9])
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$Saat menjalankan perintah di atas dalam shell python, output berikut akan dihasilkan -
[10 40 30 2 6 9]
Matriks adalah objek yang bisa berubah. Modul matriks juga menyediakan kelas ImmutableMatrix untuk mendapatkan matriks yang tidak dapat diubah.
Manipulasi dasar
Itu shape properti objek Matrix mengembalikan ukurannya.
>>> M.shapeOutput untuk kode di atas adalah sebagai berikut -
(2,3)
Metode row () dan col () masing-masing mengembalikan baris atau kolom dari nomor yang ditentukan.
>>> M.row(0)
$\displaystyle \left[\begin{matrix}10 & 40 & 30\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[10 40 30]
>>> M.col(1)
$\displaystyle \left[\begin{matrix}40\\6\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[40 6]
Gunakan operator slice Python untuk mengambil satu atau lebih item milik baris atau kolom.
>>> M.row(1)[1:3]
[6, 9]Kelas matriks memiliki metode row_del () dan col_del () yang menghapus baris / kolom tertentu dari matriks yang diberikan -
>>> M=Matrix(2,3,[10,40,30,2,6,9])
>>> M.col_del(1)
>>> MSaat menjalankan perintah di atas dalam shell python, output berikut akan dihasilkan -
Matrix([[10, 30],[ 2, 9]])Anda dapat menerapkan gaya ke output menggunakan perintah berikut -
$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
[10 30 2 9]
>>> M.row_del(0)
>>> M
$\displaystyle \left[\begin{matrix}2 & 9\end{matrix}\right]$Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
[2 9]
Demikian pula, metode row_insert () dan col_insert () menambahkan baris atau kolom pada indeks baris atau kolom tertentu
>>> M1=Matrix([[10,30]])
>>> M=M.row_insert(0,M1)
>>> M
$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
[10 40 30 2 9]
>>> M2=Matrix([40,6])
>>> M=M.col_insert(1,M2)
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
[10 40 30 6 9]
Operasi Aritmatika
Operator biasa +, - dan * ditentukan untuk melakukan penjumlahan, pengurangan, dan perkalian.
>>> M1=Matrix([[1,2,3],[3,2,1]])
>>> M2=Matrix([[4,5,6],[6,5,4]])
>>> M1+M2
$\displaystyle \left[\begin{matrix}5 & 7 & 9\\9 & 7 & 5\end{matrix}\right]$Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
[5 7 9 9 7 5]
>>> M1-M2
$\displaystyle \left[\begin{matrix}-3 & -3 & -3\\-3 & -3 & -3\end{matrix}\right]$Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
[- 3 -3 -3 -3 -3 -3]
Perkalian matriks hanya mungkin jika - Jumlah kolom dari matriks ke-1 harus sama dengan jumlah baris matriks ke-2. - Dan hasilnya akan memiliki jumlah baris yang sama dengan matriks pertama, dan jumlah kolom yang sama dengan matriks ke-2.
>>> M1=Matrix([[1,2,3],[3,2,1]])
>>> M2=Matrix([[4,5],[6,6],[5,4]])
>>> M1*M2
$\displaystyle \left[\begin{matrix}31 & 29\\29 & 31\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[31 29 29 31]
>>> M1.T
$\displaystyle \left[\begin{matrix}1 & 3\\2 & 2\\3 & 1\end{matrix}\right]$Output berikut diperoleh setelah menjalankan kode -
[1 3 2 2 3 1]
Untuk menghitung determinan matriks, gunakan metode det (). Determinan adalah nilai skalar yang dapat dihitung dari elemen-elemen matriks persegi
>>> M=Matrix(3,3,[10,20,30,5,8,12,9,6,15])
>>> M
$\displaystyle \left[\begin{matrix}10 & 20 & 30\\5 & 8 & 12\\9 & 6 & 15\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[10 20 30 5 8 12 9 6 15]
>>> M.det()Output untuk kode di atas adalah sebagai berikut -
-120
Pembangun Matriks
SymPy menyediakan banyak jenis kelas matriks khusus. Misalnya, matriks Identitas, matriks dari semua nol dan satu, dll. Kelas-kelas ini masing-masing dinamai mata, nol dan satu. Matriks identitas adalah matriks bujursangkar dengan elemen-elemen yang jatuh pada diagonal diatur ke 1, elemen lainnya adalah 0.
Example
from sympy.matrices import eye eye(3)Output
Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[1 0 0 0 1 0 0 0 1]
Dalam matriks diag, elemen pada diagonal diinisialisasi sesuai argumen yang diberikan.
>>> from sympy.matrices import diag
>>> diag(1,2,3)
$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 2 & 0\\0 & 0 & 3\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[1 0 0 0 2 0 0 0 3]
Semua elemen dalam matriks nol diinisialisasi ke 0.
>>> from sympy.matrices import zeros
>>> zeros(2,3)
$\displaystyle \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[0 0 0 0 0 0]
Demikian pula, satuan adalah matriks dengan semua elemen disetel ke 1.
>>> from sympy.matrices import ones
>>> ones(2,3)
$\displaystyle \left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]$Output untuk kode di atas adalah sebagai berikut -
[1 1 1 1 1 1]
Paket Sympy memiliki kelas Fungsi, yang didefinisikan dalam modul sympy.core.function. Ini adalah kelas dasar untuk semua fungsi matematika yang diterapkan, juga sebagai konstruktor untuk kelas fungsi yang tidak ditentukan.
Kategori fungsi berikut diwarisi dari kelas Fungsi -
- Fungsi untuk bilangan kompleks
- Fungsi trigonometri
- Fungsi untuk bilangan bulat
- Fungsi kombinatorial
- Fungsi lain-lain
Fungsi untuk bilangan kompleks
Kumpulan fungsi ini didefinisikan di sympy.functions.elementary.complexes modul.
re
Fungsi ini mengembalikan bagian nyata dari ekspresi -
>>> from sympy import *
>>> re(5+3*I)Output untuk potongan kode di atas diberikan di bawah ini -
5
>>> re(I)Output dari potongan kode di atas adalah -
0
Im
Fungsi ini mengembalikan bagian imajiner dari sebuah ekspresi -
>>> im(5+3*I)Output untuk potongan kode di atas diberikan di bawah ini -
3
>>> im(I)Output untuk potongan kode di atas diberikan di bawah ini -
1
sign
Fungsi ini mengembalikan tanda kompleks dari sebuah ekspresi.
Untuk ekspresi nyata, tandanya adalah -
- 1 jika ekspresi positif
- 0 jika ekspresi sama dengan nol
- -1 jika ekspresi negatif
Jika ekspresi imajiner, tanda yang dikembalikan adalah -
- Saya jika im (ekspresi) positif
- -Aku jika im (ekspresi) negatif
>>> sign(1.55), sign(-1), sign(S.Zero)Output untuk potongan kode di atas diberikan di bawah ini -
(1, -1, 0)
>>> sign (-3*I), sign(I*2)Output untuk potongan kode di atas diberikan di bawah ini -
(-I, I)
Abs
Fungsi ini mengembalikan nilai absolut dari bilangan kompleks. Ini didefinisikan sebagai jarak antara titik asal (0,0) dan titik (a, b) di bidang kompleks. Fungsi ini merupakan perpanjangan dari fungsi built-in abs () untuk menerima nilai simbolik.
>>> Abs(2+3*I)Output untuk potongan kode di atas diberikan di bawah ini -
$\sqrt13$
conjugate
Fungsi ini mengembalikan konjugasi dari bilangan kompleks. Untuk mencari konjugat kompleks kita mengubah tanda dari bagian imajiner.
>>> conjugate(4+7*I)Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
4 - 7i
Fungsi trigonometri
SymPy memiliki definisi untuk semua rasio trigonometri - sin cos, tan dll serta kebalikannya seperti asin, acos, atan dll. Fungsi ini menghitung nilai masing-masing untuk sudut tertentu yang dinyatakan dalam radian.
>>> sin(pi/2), cos(pi/4), tan(pi/6)Output untuk potongan kode di atas diberikan di bawah ini -
(1, sqrt(2)/2, sqrt(3)/3)
>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)Output untuk potongan kode di atas diberikan di bawah ini -
(pi/2, pi/4, pi/6)
Fungsi pada Bilangan Bulat
Ini adalah sekumpulan fungsi untuk melakukan berbagai operasi pada bilangan bulat.
ceiling
Ini adalah fungsi univariate yang mengembalikan nilai integer terkecil tidak kurang dari argumennya. Dalam kasus bilangan kompleks, plafon bagian nyata dan imajiner terpisah.
>>> ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)Output untuk potongan kode di atas diberikan di bawah ini -
(4, 7, 3 + 4*I)
floor
Fungsi ini mengembalikan nilai integer terbesar yang tidak lebih besar dari argumennya. Dalam kasus bilangan kompleks, fungsi ini juga mengambil dasar bagian nyata dan imajiner secara terpisah.
>>> floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)Output untuk potongan kode di atas diberikan di bawah ini -
(3, 16, 6 - 6*I)
frac
Fungsi ini mewakili bagian pecahan dari x.
>>> frac(3.99), frac(Rational(10,3)), frac(10)Output untuk potongan kode di atas diberikan di bawah ini -
(0.990000000000000, 1/3, 0)
Fungsi kombinatorial
Kombinatorika adalah bidang matematika yang berkaitan dengan masalah pemilihan, pengaturan, dan operasi dalam sistem terbatas atau diskrit.
factorial
Faktorial sangat penting dalam kombinatorika di mana ia memberikan jumlah cara di mana n objek dapat diubah. Ini secara simbolis direpresentasikan sebagai ð ?? '¥! Fungsi ini merupakan implementasi fungsi faktorial di atas bilangan bulat nonnegatif, faktorial dari bilangan bulat negatif adalah kompleks tak terhingga.
>>> x=Symbol('x')
>>> factorial(x)Output untuk potongan kode di atas diberikan di bawah ini -
x!
>>> factorial(5)Output untuk potongan kode di atas diberikan di bawah ini -
120
>>> factorial(-1)Output untuk potongan kode di atas diberikan di bawah ini -
$\infty\backsim$
binomium
Fungsi ini jumlah cara kita dapat memilih k elemen dari himpunan n elemen.
>>> x,y=symbols('x y')
>>> binomial(x,y)Output untuk potongan kode di atas diberikan di bawah ini -
$(\frac{x}{y})$
>>> binomial(4,2)Output untuk potongan kode di atas diberikan di bawah ini -
6
Barisan segitiga Pascal dapat dibuat dengan fungsi binomial.
>>> for i in range(5): print ([binomial(i,j) for j in range(i+1)])Anda mendapatkan output berikut setelah menjalankan cuplikan kode di atas -
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
fibonacci
Bilangan Fibonacci adalah deret bilangan bulat yang ditentukan oleh suku awal F0 = 0, F1 = 1 dan relasi pengulangan dua suku Fn = Fnâˆ'1 + Fnâˆ'2.
>>> [fibonacci(x) for x in range(10)]Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
tribonacci
Angka-angka Tribonacci adalah urutan bilangan bulat yang ditentukan oleh istilah awal F0 = 0, F1 = 1, F2 = 1 dan hubungan pengulangan tiga istilah Fn = Fn-1 + Fn-2 + Fn-3.
>>> tribonacci(5, Symbol('x'))Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^8 + 3x^5 + 3x^2$
>>> [tribonacci(x) for x in range(10)]Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]
Fungsi Miscellaneous
Berikut adalah daftar beberapa fungsi yang sering digunakan -
Min- Mengembalikan nilai minimum daftar. Ini dinamai Min untuk menghindari konflik dengan fungsi built-in min.
Max- Mengembalikan nilai maksimum daftar. Ini dinamai Max untuk menghindari konflik dengan fungsi max built-in.
root - Mengembalikan akar ke n dari x.
sqrt - Mengembalikan akar kuadrat utama dari x.
cbrt - Fungsi ini menghitung akar pangkat tiga utama dari x, (pintasan untuk x ++ Rasional (1,3)).
Berikut ini adalah contoh dari fungsi miscellaneous di atas dan keluarannya masing-masing -
>>> Min(pi,E)e
>>> Max(5, Rational(11,2))$\frac{11}{2}$
>>> root(7,Rational(1,2))49
>>> sqrt(2)$\sqrt2$
>>> cbrt(1000)10
Dalam matematika, sistem bilangan kuarter merupakan perpanjangan dari bilangan kompleks. Setiap objek Kuarter berisi empat variabel skalar dan empat dimensi, satu dimensi nyata dan tiga dimensi imajiner.
Quaternion diwakili oleh ekspresi berikut -
q = a + bi + cj + dk
dimana a, b, c dan d adalah bilangan real dan i, j, k adalah unit kuarternasi sehingga, i2 == j2 == k2 == ijk
Itu sympy.algebras.quaternion modul memiliki kelas Quaternion.
>>> from sympy.algebras.quaternion import Quaternion
>>> q=Quaternion(2,3,1,4)
>>> qPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$2 + 3i + 1j + 4k$
Kuarter digunakan dalam matematika murni, serta dalam matematika terapan, grafik komputer, visi komputer, dll.
>>> from sympy import *
>>> x=Symbol('x')
>>> q1=Quaternion(x**2, x**3, x) >>> q1Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$x^2 + x^3i + xj + 0k$
Objek kuarter juga dapat memiliki koefisien imajiner
>>> q2=Quaternion(2,(3+2*I), x**2, 3.5*I)
>>> q2Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$2 + (3 + 2i)i + x2j + 3.5ik$
Menambahkan()
Metode yang tersedia di kelas Quaternion ini melakukan penambahan dua objek Quaternion.
>>> q1=Quaternion(1,2,3,4)
>>> q2=Quaternion(4,3,2,1)
>>> q1.add(q2)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$5 + 5i + 5j + 5k$
Dimungkinkan untuk menambahkan angka atau simbol dalam objek Quaternion.
>>> q1+2Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
$3 + 2i + 3j + 4k$
>>> q1+xOutput berikut diperoleh setelah menjalankan cuplikan kode di atas -
$(x + 1) + 2i + 3j + 4k$
mul ()
Metode ini melakukan perkalian dua objek angka empat.
>>> q1=Quaternion(1,2,1,2)
>>> q2=Quaternion(2,4,3,1)
>>> q1.mul(q2)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$(-11) + 3i + 11j + 7k$
terbalik()
Metode ini mengembalikan invers dari objek quaternion.
>>> q1.inverse()Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{1}{10} + (-\frac{1}{5})i + (-\frac{1}{10})j + (-\frac{1}{5})k$
pow ()
Metode ini mengembalikan kekuatan objek quaternion.
>>> q1.pow(2)Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
$(-8) + 4i + 2j + 4k$
exp ()
Metode ini menghitung eksponensial dari objek Kuarter yaitu persamaan
>>> q=Quaternion(1,2,4,3)
>>> q.exp()Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
$e\cos(\sqrt29) + \frac{2\sqrt29e\sin(\sqrt29)}{29}i + \frac{4\sqrt29e\sin(\sqrt29)}{29}j + \frac{3\sqrt29e\sin}{29}k$
Karena simbol = dan == didefinisikan sebagai penugasan dan operator persamaan di Python, mereka tidak dapat digunakan untuk merumuskan persamaan simbolik. SymPy menyediakan fungsi Persamaan () untuk menyiapkan persamaan.
>>> from sympy import *
>>> x,y=symbols('x y')
>>> Eq(x,y)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
x = y
Karena x = y dimungkinkan jika dan hanya jika xy = 0, persamaan di atas dapat ditulis sebagai -
>>> Eq(x-y,0)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
x − y = 0
Modul solver di SymPy menyediakan fungsi soveset () yang prototipe-nya adalah sebagai berikut -
solveset(equation, variable, domain)Domain secara default adalah S.Complexes. Menggunakan fungsi solveset (), kita dapat menyelesaikan persamaan aljabar sebagai berikut -
>>> solveset(Eq(x**2-9,0), x)Output berikut diperoleh -
{−3, 3}
>>> solveset(Eq(x**2-3*x, -2),x)Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
{1,2}
Output dari solveset adalah FiniteSet dari solusi. Jika tidak ada solusi, EmptySet dikembalikan
>>> solveset(exp(x),x)Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
$\varnothing$
Persamaan linier
Kita harus menggunakan fungsi linsolve () untuk menyelesaikan persamaan linier.
Misalnya persamaannya adalah sebagai berikut -
xy = 4
x + y = 1
>>> from sympy import *
>>> x,y=symbols('x y')
>>> linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$
Fungsi linsolve () juga dapat menyelesaikan persamaan linier yang dinyatakan dalam bentuk matriks.
>>> a,b=symbols('a b')
>>> a=Matrix([[1,-1],[1,1]])
>>> b=Matrix([4,1])
>>> linsolve([a,b], (x,y))Kami mendapatkan output berikut jika kami menjalankan cuplikan kode di atas -
$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$
Persamaan non-linier
Untuk tujuan ini, kami menggunakan fungsi nonlinsolve (). Persamaan untuk contoh ini -
a 2 + a = 0 ab = 0
>>> a,b=symbols('a b')
>>> nonlinsolve([a**2 + a, a - b], [a, b])Kami mendapatkan output berikut jika kami menjalankan cuplikan kode di atas -
$\lbrace(-1, -1),(0,0)\rbrace$
persamaan diferensial
Pertama, buat fungsi tak terdefinisi dengan meneruskan cls = Fungsi ke fungsi simbol. Untuk menyelesaikan persamaan diferensial, gunakan dsolve.
>>> x=Symbol('x')
>>> f=symbols('f', cls=Function)
>>> f(x)Output berikut diperoleh setelah menjalankan cuplikan kode di atas -
f(x)
Di sini f (x) adalah fungsi yang tidak dievaluasi. Turunannya adalah sebagai berikut -
>>> f(x).diff(x)Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$\frac{d}{dx}f(x)$
Pertama kita buat objek Persamaan yang sesuai dengan persamaan diferensial berikut
>>> eqn=Eq(f(x).diff(x)-f(x), sin(x))
>>> eqnPotongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$-f(x) + \frac{d}{dx}f(x)= \sin(x)$
>>> dsolve(eqn, f(x))Potongan kode di atas memberikan keluaran yang setara dengan ekspresi di bawah ini -
$f(x)=(c^1-\frac{e^-xsin(x)}{2}-\frac{e^-xcos(x)}{2})e^x$
SymPy menggunakan pustaka Matplotlib sebagai backend untuk merender plot 2-D dan 3-D fungsi matematika. Pastikan Matplotlib tersedia dalam instalasi Python saat ini. Jika tidak, instal yang sama menggunakan perintah berikut -
pip install matplotlibDukungan plotting didefinisikan dalam modul sympy.plotting. Fungsi-fungsi berikut hadir dalam modul plotting -
plot - Plot garis 2D
plot3d - Plot garis 3D
plot_parametric - Plot parametrik 2D
plot3d_parametric - Plot parametrik 3D
Fungsi plot () mengembalikan turunan dari kelas Plot. Gambar plot mungkin memiliki satu atau lebih ekspresi SymPy. Meskipun mampu menggunakan Matplotlib sebagai backend, backend lain seperti texplot, pyglet, atau API bagan Google juga dapat digunakan.
plot(expr, range, kwargs)di mana expr adalah ekspresi symPy yang valid. Jika tidak disebutkan, range menggunakan default sebagai (-10, 10).
Contoh berikut memplot nilai x2 untuk setiap nilai dalam rentang (-10,10) -
>>> from sympy.plotting import plot
>>> from sympy import *
>>> x=Symbol('x')
>>> plot(x**2, line_color='red')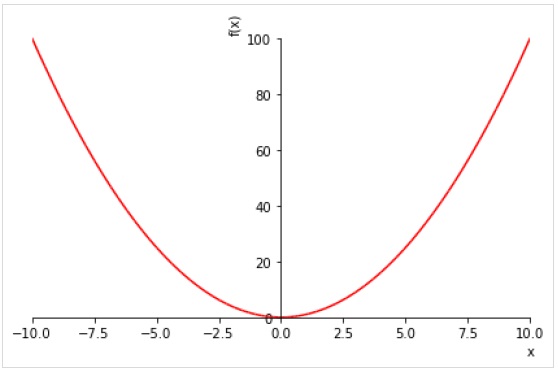
Untuk menggambar beberapa plot untuk rentang yang sama, berikan beberapa ekspresi sebelum tupel rentang.
>>> plot( sin(x),cos(x), (x, -pi, pi))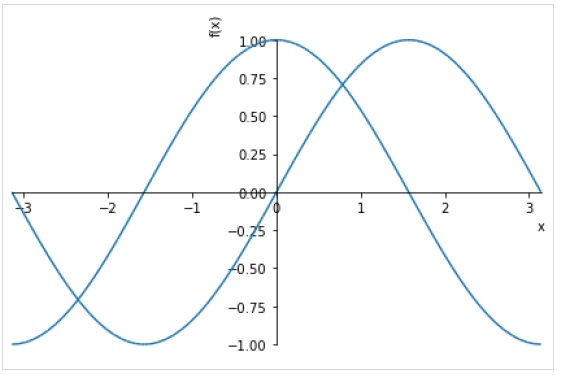
Anda juga dapat menentukan rentang terpisah untuk setiap ekspresi.
plot((expr1, range1), (expr2, range2))Gambar berikut memplot sin (x) dan cos (x) pada rentang yang berbeda.
>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)))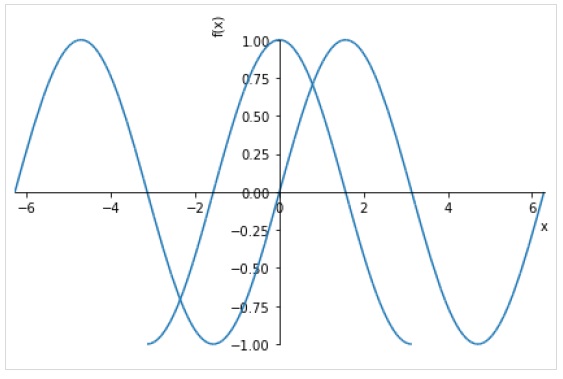
Argumen kata kunci opsional berikut mungkin ditentukan dalam fungsi plot ().
line_color - menentukan warna garis plot.
title - string untuk ditampilkan sebagai judul
xlabel - string yang akan ditampilkan sebagai label untuk sumbu X.
ylabel - string yang akan ditampilkan sebagai label untuk sumbu y
>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)), line_color='red', title='SymPy plot example')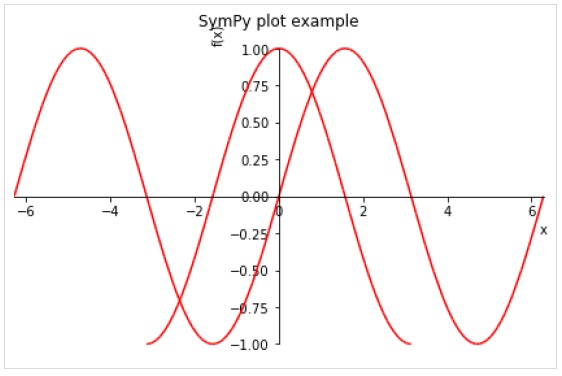
Fungsi plot3d () menampilkan plot tiga dimensi.
plot3d(expr, xrange, yrange, kwargs)Contoh berikut menggambar plot permukaan 3D -
>>> from sympy.plotting import plot3d
>>> x,y=symbols('x y')
>>> plot3d(x*y, (x, -10,10), (y, -10,10))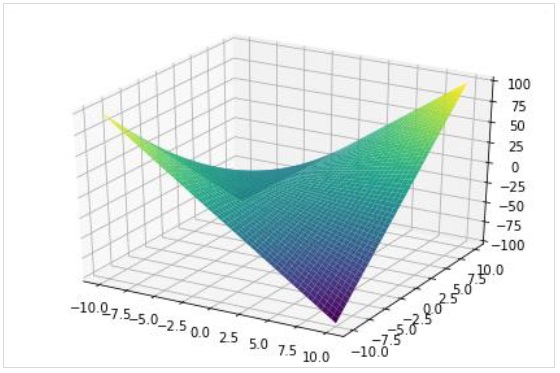
Seperti pada plot 2D, plot tiga dimensi juga dapat memiliki beberapa plot yang masing-masing memiliki jarak yang berbeda.
>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))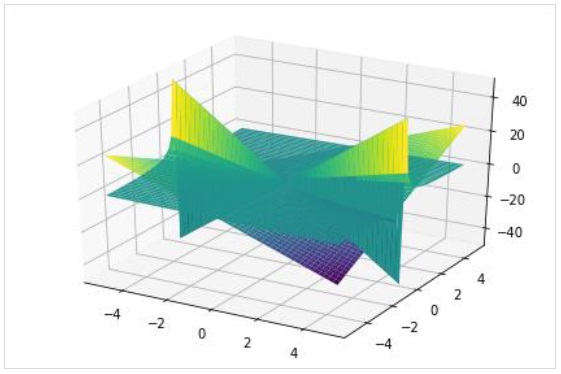
Fungsi plot3d_parametric_line () membuat plot garis parametrik 3 dimensi.
>>> from sympy.plotting import plot3d_parametric_line
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))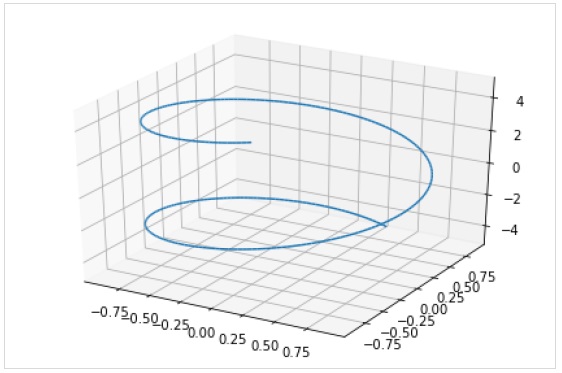
Untuk menggambar plot permukaan parametrik, gunakan fungsi plot3d_parametric_surface ().
plot3d_parametric_surface(xexpr, yexpr, zexpr, rangex, rangey, kwargs)
>>> from sympy.plotting import plot3d_parametric_surface
>>> plot3d_parametric_surface(cos(x+y), sin(x-y), x-y, (x, -5, 5), (y, -5, 5))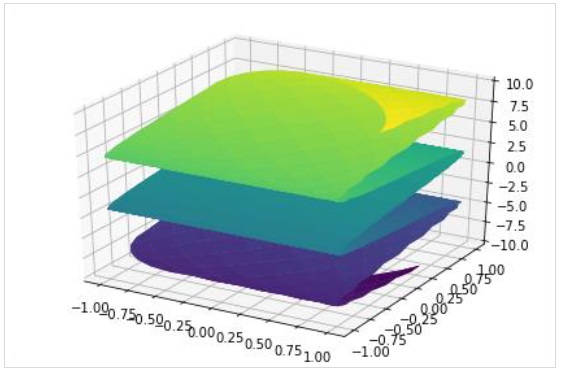
Modul geometri di SymPy memungkinkan pembuatan entitas dua dimensi seperti garis, lingkaran, dll. Kemudian kita dapat memperoleh informasi tentangnya seperti memeriksa kolinearitas atau menemukan persimpangan.
Titik
Kelas titik mewakili satu titik dalam ruang Euclidean. Contoh berikut memeriksa collinearity poin -
>>> from sympy.geometry import Point
>>> from sympy import *
>>> x=Point(0,0)
>>> y=Point(2,2)
>>> z=Point(4,4)
>>> Point.is_collinear(x,y,z)Output
True
>>> a=Point(2,3)
>>> Point.is_collinear(x,y,a)Output
False
Metode jarak () kelas Titik menghitung jarak antara dua titik
>>> x.distance(y)Output
$2\sqrt2$
Jarak juga dapat direpresentasikan dalam bentuk simbol.
Garis
Entitas garis diperoleh dari dua objek Titik. Metode intersection () mengembalikan titik perpotongan jika dua garis saling berpotongan.
>>> from sympy.geometry import Point, Line
>>> p1, p2=Point(0,5), Point(5,0)
>>> l1=Line(p1,p2)
>>> l2=Line(Point(0,0), Point(5,5))
>>> l1.intersection(l2)Output
[Point2D(5/2, 5/2)]
>>> l1.intersection(Line(Point(0,0), Point(2,2)))Output
[Point2D(5/2, 5/2)]
>>> x,y=symbols('x y')
>>> p=Point(x,y)
>>> p.distance(Point(0,0))Output
$\sqrt{x^2 + y^2}$
Segi tiga
Fungsi ini membangun entitas segitiga dari objek tiga titik.
Triangle(a,b,c)
>>> t=Triangle(Point(0,0),Point(0,5), Point(5,0))
>>> t.areaOutput
$-\frac{25}{2}$
Elips
Entitas geometri elips dibangun dengan melewatkan objek Titik yang sesuai dengan pusat dan dua angka masing-masing untuk jari-jari horizontal dan vertikal.
ellipse(center, hradius, vradius)
>>> from sympy.geometry import Ellipse, Line
>>> e=Ellipse(Point(0,0),8,3)
>>> e.areaOutput
$24\pi$
Vradius dapat diberikan secara tidak langsung dengan menggunakan parameter eksentrisitas.
>>> e1=Ellipse(Point(2,2), hradius=5, eccentricity=Rational(3,4))
>>> e1.vradiusOutput
$\frac{5\sqrt7}{4}$
Itu apoapsis elips adalah jarak terjauh antara fokus dan kontur.
>>> e1.apoapsisOutput
$\frac{35}{4}$
Pernyataan berikut menghitung keliling elips -
>>> e1.circumferenceOutput
$20E(\frac{9}{16})$
Itu equation metode persamaan pengembalian elips dari elips.
>>> e1.equation(x,y)Output
$(\frac{x}{5}-\frac{2}{5})^2 + \frac{16(y-2)2}{175} - 1$
Dalam matematika, himpunan adalah kumpulan objek berbeda yang terdefinisi dengan baik yang mungkin berupa angka, orang, huruf alfabet, atau bahkan himpunan lainnya. Set juga merupakan salah satu tipe bawaan di Python. SymPy menyediakan modul set. Ini berisi definisi berbagai jenis himpunan dan memiliki fungsionalitas untuk melakukan operasi himpunan seperti persimpangan, penyatuan, dll.
Set adalah kelas dasar untuk jenis set lainnya di SymPy. Perhatikan bahwa ini berbeda dari tipe data set bawaan Python. Kelas interval mewakili interval nyata dan properti batasnya mengembalikan aFiniteSet obyek.
>>> from sympy import Interval
>>> s=Interval(1,10).boundary
>>> type(s)sympy.sets.sets.FiniteSet
FiniteSet adalah kumpulan nomor diskrit. Itu dapat diperoleh dari objek sekuens apa pun seperti daftar atau string.
>>> from sympy import FiniteSet
>>> FiniteSet(range(5))Output
$\lbrace\lbrace0,1,...,4\rbrace\rbrace$
>>> numbers=[1,3,5,2,8]
>>> FiniteSet(*numbers)Output
$\lbrace1,2,3,5,8\rbrace$
>>> s="HelloWorld"
>>> FiniteSet(*s)Output
{H,W,d,e,l,o,r}
Perhatikan bahwa, seperti pada set bawaan, Kumpulan SymPy juga merupakan kumpulan objek yang berbeda.
ConditionSet adalah sekumpulan elemen yang memenuhi kondisi tertentu
>>> from sympy import ConditionSet, Eq, Symbol
>>> x=Symbol('x')
>>> s=ConditionSet(x, Eq(x**2-2*x,0), Interval(1,10)) >>> sOutput
$\lbrace x\mid x\in[1,10]∧x^2 - 2x =0\rbrace$
Unionadalah himpunan gabungan. Ini mencakup semua elemen dalam dua set. Perhatikan bahwa elemen yang ditemukan di keduanya, hanya akan muncul sekali di Union.
>>> from sympy import Union
>>> l1=[3,1,5,7]
>>> l2=[9,7,2,1]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> Union(a,b)Intersection di sisi lain hanya berisi elemen-elemen yang ada di keduanya.
>>> from sympy import Intersection
>>> Intersection(a,b)ProductSet objek mewakili produk Kartesius dari elemen di kedua set.
>>> from sympy import ProductSet
>>> l1=[1,2]
>>> l2=[2,3]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> set(ProductSet(a,b))Complement(a,b) mempertahankan elemen dalam elemen pengecualian yang sama dengan himpunan b.
>>> from sympy import Complement
>>> l1=[3,1,5,7]
>>> l2=[9,7,2,1]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> Complement(a,b), Complement(b,a)SymmetricDifference set hanya berisi elemen yang tidak umum di kedua set.
>>> from sympy import SymmetricDifference
>>> l1=[3,1,5,7]
>>> l2=[9,7,2,1]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> SymmetricDifference(a,b)Output
{2,3,5,9}
Ada beberapa printer yang tersedia di SymPy. Berikut ini adalah sebagian daftar -
- str
- srepr
- Printer cantik ASCII
- Unicode printer cantik
- LaTeX
- MathML
- Dot
Objek SymPy juga dapat dikirim sebagai output ke kode berbagai bahasa, seperti C, Fortran, Javascript, Theano, dan Python.
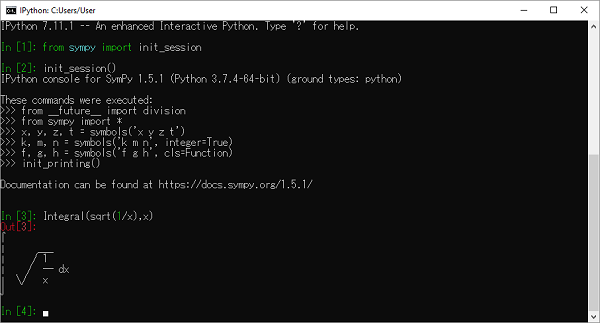
SymPy menggunakan karakter Unicode untuk membuat keluaran dalam bentuk cetakan cantik. Jika Anda menggunakan konsol Python untuk menjalankan sesi SymPy, lingkungan pencetakan terbaik yang cantik diaktifkan dengan memanggil fungsi init_session ().
>>> from sympy import init_session
>>> init_session()Konsol IPython untuk SymPy 1.5.1 (Python 3.7.4-64-bit) (tipe dasar: python).
Perintah-perintah ini dijalankan -
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()Dokumentasi dapat ditemukan di https://docs.sympy.org/1.5.1/.
>>> Integral(sqrt(1/x),x)$\int \sqrt\frac{1}{x} dx$
Jika LATEX tidak diinstal, tetapi Matplotlib diinstal, itu akan menggunakan mesin rendering Matplotlib. Jika Matplotlib tidak diinstal, ia menggunakan printer cantik Unicode. Namun, notebook Jupyter menggunakan MathJax untuk merender LATEX.
Di terminal yang tidak mendukung Unicode, printer cantik ASCII digunakan.
Untuk menggunakan printer ASCII gunakan fungsi pprint () dengan properti use_unicode disetel ke False
>>> pprint(Integral(sqrt(1/x),x),use_unicode=False)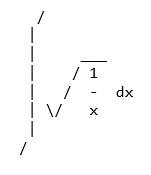
Printer cantik Unicode juga diakses dari pprint () dan pretty (). Jika terminal mendukung Unicode, itu digunakan secara otomatis. Jika pprint () tidak dapat mendeteksi bahwa terminal mendukung unicode, Anda dapat meneruskan use_unicode = True untuk memaksanya menggunakan Unicode.
Untuk mendapatkan bentuk LATEX dari sebuah ekspresi, gunakan fungsi latex ().
>>> print(latex(Integral(sqrt(1/x),x)))\int \sqrt{\frac{1}{x}}\, dx
Anda juga dapat menggunakan printer mathml. untuk tujuan itu, impor fungsi print_mathml. Versi string diperoleh dengan fungsi mathml ().
>>> from sympy.printing.mathml import print_mathml
>>> print_mathml(Integral(sqrt(1/x),x))<apply>
<int/>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<root/>
<apply>
<power/>
<ci>x</ci>
<cn>-1</cn>
</apply>
</apply>
</apply>
>>>mathml(Integral(sqrt(1/x),x))'<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn>-1</cn></apply></apply></apply>'