Collegamenti del circuito nei resistori
Un resistore quando collegato in un circuito, tale connessione può essere in serie o in parallelo. Facci ora sapere cosa accadrà ai valori totali di corrente, tensione e resistenza se sono collegati anche in serie, se collegati in parallelo.
Resistori in serie
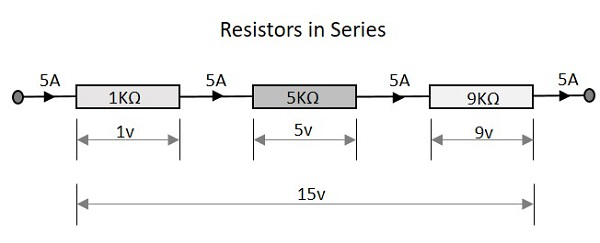
Osserviamo cosa succede quando poche resistenze sono collegate in serie. Consideriamo tre resistori con valori diversi, come mostrato nella figura sotto.
Resistenza
La resistenza totale di un circuito con resistenze in serie è uguale alla somma delle singole resistenze. Ciò significa che nella figura sopra ci sono tre resistori con i valori 1KΩ, 5KΩ e 9KΩ rispettivamente.
Il valore di resistenza totale della rete di resistori è -
$$ R \: \: = \: \: R_ {1} \: + \: R_ {2} \: + \: R_ {3} $$
Il che significa che 1 + 5 + 9 = 15KΩ è la resistenza totale.
Dove R 1 è la resistenza del 1 ° resistore, R 2 è la resistenza del 2 ° resistore e R 3 è la resistenza del 3 ° resistore in rete resistore sopra.
Voltaggio
La tensione totale che appare su una rete di resistori in serie è l'aggiunta delle cadute di tensione a ogni singola resistenza. Nella figura sopra abbiamo tre diversi resistori che hanno tre diversi valori di cadute di tensione in ogni fase.
Tensione totale che appare attraverso il circuito -
$$ V \: \: = \: \: V_ {1} \: + \: V_ {2} \: + \: V_ {3} $$
Il che significa che 1v + 5v + 9v = 15v è la tensione totale.
Dove V 1 è la caduta di tensione di 1 ° resistore, V 2 è la caduta di tensione di 2 ° resistore e V 3 è la caduta di tensione del 3 ° resistore in rete resistore sopra.
attuale
La quantità totale di corrente che scorre attraverso un set di resistori collegati in serie è la stessa in tutti i punti della rete di resistori. Quindi la corrente è la stessa 5A quando misurata all'ingresso o in qualsiasi punto tra le resistenze o anche all'uscita.
Corrente attraverso la rete -
$$ I \: \: = \: \: I_ {1} \: = \: I_ {2} \: = \: I_ {3} $$
Il che significa che la corrente in tutti i punti è 5A.
Dove I 1 è la corrente attraverso il 1 ° resistore, ho 2 è la corrente attraverso il 2 ° resistore e 3 è la corrente attraverso il 3 ° resistore in rete resistore sopra.
Resistenze in parallelo
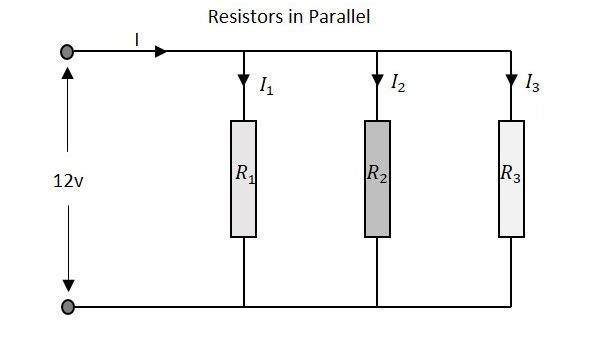
Osserviamo cosa succede quando poche resistenze sono collegate in Parallelo. Consideriamo tre resistori con valori diversi, come mostrato nella figura sotto.
Resistenza
La resistenza totale di un circuito con resistori in parallelo viene calcolata in modo diverso dal metodo della rete di resistori in serie. Qui, il valore reciproco (1 / R) delle resistenze individuali viene aggiunto con l'inverso della somma algebrica per ottenere il valore della resistenza totale.
Il valore di resistenza totale della rete di resistori è -
$$ \ frac {1} {R} \: \: = \: \: \ frac {1} {R_ {1}} \: \: + \: \: \ frac {1} {R_ {2}} \: \: + \ frac {1} {R_ {3}} $$
Dove R 1 è la resistenza del 1 ° resistore, R 2 è la resistenza del 2 ° resistore e R 3 è la resistenza del 3 ° resistore in rete resistore sopra.
Ad esempio, se si considerano i valori di resistenza dell'esempio precedente, ciò significa R 1 = 1KΩ, R 2 = 5KΩ e R 3 = 9KΩ. La resistenza totale della rete di resistori paralleli sarà:
$$ \ frac {1} {R} \: \: = \: \: \ frac {1} {1} \: \: + \: \: \ frac {1} {5} \: \: + \ frac {1} {9} $$
$$ = \: \: \ frac {45 \: \: + \: \: 9 \: \: + \: \: 5} {45} \: \: = \: \: \ frac {59} { 45} $$
$$ R \: \: = \: \: \ frac {45} {59} \: \: = \: \: 0.762K \ Omega \: \: = \: \: 76.2 \ Omega $$
Dal metodo che abbiamo per calcolare la resistenza parallela, possiamo derivare una semplice equazione per una rete parallela a due resistori. È -
$$ R \: \: = \: \: \ frac {R_ {1} \: \: \ times \: \: R_ {2}} {R_ {1} \: \: + \: \: R_ { 2}} \: $$
Voltaggio
La tensione totale che appare su una rete di resistori paralleli è la stessa delle cadute di tensione su ogni singola resistenza.
La tensione che appare attraverso il circuito -
$$ V \: \: = \: \: V_ {1} \: = \: V_ {2} \: = \: V_ {3} $$
Dove V 1 è la caduta di tensione di 1 ° resistore, V 2 è la caduta di tensione di 2 ° resistore e V 3 è la caduta di tensione del 3 ° resistore in rete resistore sopra. Quindi la tensione è la stessa in tutti i punti di una rete di resistori paralleli.
attuale
La quantità totale di corrente che entra in una rete resistiva parallela è la somma di tutte le singole correnti che fluiscono in tutti i rami paralleli. Il valore di resistenza di ogni ramo determina il valore della corrente che lo attraversa. La corrente totale attraverso la rete è
$$ I \: \: = \: \: I_ {1} \: + \: I_ {2} \: + \: I_ {3} $$
Dove I 1 è la corrente attraverso il 1 ° resistore, ho 2 è la corrente attraverso il 2 ° resistore e 3 è la corrente attraverso il 3 ° resistore in rete resistore sopra. Quindi la somma delle singole correnti in diversi rami ottiene la corrente totale in una rete resistiva parallela.
Un resistore è particolarmente utilizzato come carico nell'uscita di molti circuiti. Se il carico resistivo non viene utilizzato, viene posizionato un resistore prima di un carico. Il resistore è solitamente un componente di base in qualsiasi circuito.