Elettronica di base - Induttanza
La proprietà di un induttore di ottenere la tensione indotta dalla variazione del flusso di corrente è definita Induttanza. L'induttanza è il rapporto tra la tensione e la velocità di variazione della corrente.
La velocità di variazione della corrente produce un cambiamento nel campo magnetico, che induce un EMF in direzione opposta alla sorgente di tensione. Questa proprietà di induzione dell'EMF è chiamata comeInductance.
La formula per l'induttanza è
$$ Induttanza \: \: = \: \: \ frac {volatge} {rate \: of \: change \: of \: current} $$
Units −
L'unità di induttanza è Henry. È indicato daL.
Gli induttori sono per lo più disponibili in mH (milli Henry) e μH (micro Henry).
Si dice che una bobina abbia un'induttanza di one Henry quando un EMF di one volt è autoindotto nella bobina in cui la corrente che scorre è cambiata a una velocità di one ampere per second.
Autoinduttanza
Se si considera una bobina in cui scorre una certa corrente, ha un campo magnetico, perpendicolare al flusso di corrente. Quando questa corrente continua a variare, cambia anche il campo magnetico e questo campo magnetico mutevole, induce un EMF, opposto alla tensione della sorgente. Questo EMF opposto prodotto è ilself-induced voltage e questo metodo è chiamato come self-inductance.
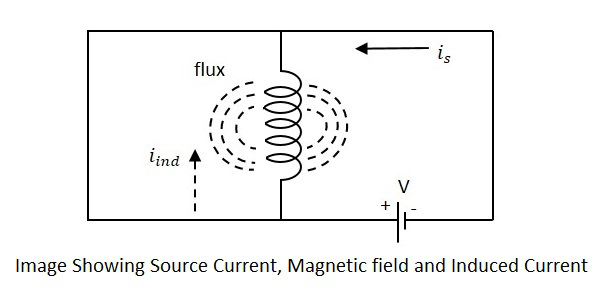
Il corrente is in figura indicare la sorgente di corrente while iindindica la corrente indotta. Il flusso rappresenta il flusso magnetico creato attorno alla bobina. Con l'applicazione della tensione, la correnteisflussi e flusso vengono creati. Quando la correnteis varia, il flusso viene variato producendo iind.
Questo EMF indotto attraverso la bobina è proporzionale alla velocità di variazione della corrente. Maggiore è il tasso di variazione della corrente, maggiore è il valore dell'EMF indotto.
Possiamo scrivere l'equazione sopra come
$$ E \: \: \ alpha \: \: \ frac {dI} {dt} $$
$$ E \: \: = \: \: L \: \: \ frac {dI} {dt} $$
Dove,
E è l'EMF prodotto
dI/dt indica la velocità di variazione della corrente
L indica il coefficiente di induttanza.
L'autoinduttanza o il coefficiente di autoinduttanza possono essere definiti come
$$ L \: \: = \: \: \ frac {E} {\ frac {dI} {dt}} $$
L'equazione effettiva è scritta come
$$ E \: \: = \: \: - L \: \: \ frac {dI} {dt} $$
Il meno nell'equazione precedente lo indica the EMF is induced in opposite direction to the voltage source secondo la legge di Lenz.
Induttanza reciproca
Poiché la bobina che trasporta corrente produce un campo magnetico attorno ad essa, se un'altra bobina viene avvicinata a questa bobina, in modo tale che si trovi nella regione del flusso magnetico del primario, il flusso magnetico variabile induce un EMF nella seconda bobina. Se questa prima bobina è chiamata comePrimary coil, il secondo può essere chiamato come file Secondary coil.
Quando l'EMF è indotto nella bobina secondaria a causa del campo magnetico variabile della bobina primaria, allora tale fenomeno è chiamato come il Mutual Inductance.
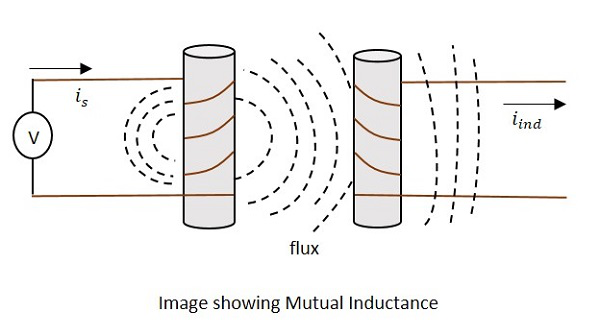
Il corrente is in figura indicare la sorgente di corrente while iindindica la corrente indotta. Il flusso rappresenta il flusso magnetico creato attorno alla bobina. Questo si diffonde anche alla bobina secondaria.
Con l'applicazione della tensione, la corrente isflussi e flusso vengono creati. Quando la correnteis varia, il flusso viene variato producendo iind nella bobina secondaria, a causa della proprietà di mutua induttanza.
Il cambiamento è avvenuto così.
$$ V_ {p} \: \: I_ {p} \ rightarrow \: \: B \: \: \ rightarrow \: \: V_ {s} \: \: I_ {s} $$
Dove,
Vp ip Indicare rispettivamente la tensione e la corrente nella bobina primaria
B Indica il flusso magnetico
Vs is Indicare rispettivamente la tensione e la corrente nella bobina secondaria
Mutua induttanza M dei due circuiti descrive la quantità di tensione nel secondario indotta dalle variazioni di corrente del primario.
$$ V (Secondario) \: \: = \: \: - M \ frac {\ Delta I} {\ Delta t} $$
Dove $ \ frac {\ Delta I} {\ Delta t} $ il tasso di variazione della corrente con il tempo e Mè il coefficiente di mutua induttanza. Il segno meno indica che la direzione della corrente è opposta alla sorgente.
Units −
Le unità di mutua induttanza sono
$$ volt \: \: = \: \: M \ frac {amps} {sec} $$
(Dall'equazione precedente)
$$ M \: \: = \: \: \ frac {volt. \: Sec} {amp} $$
$$ = \: \: Henry (H) $$
A seconda del numero di spire delle bobine primaria e secondaria, il collegamento del flusso magnetico e la quantità di EMF indotta variano. Il numero di turni nella primaria è indicato con N1 e nel secondario con N2. Il coefficiente di accoppiamento è il termine che specifica la mutua induttanza delle due bobine.
Fattori che influenzano l'induttanza
Ci sono alcuni fattori che influenzano le prestazioni di un induttore. I principali sono discussi di seguito.
Lunghezza della bobina
La lunghezza della bobina dell'induttore è inversamente proporzionale all'induttanza della bobina. Se la lunghezza della bobina è maggiore, l'induttanza offerta da quell'induttore diminuisce e viceversa.
Area della sezione trasversale della bobina
L'area della sezione trasversale della bobina è direttamente proporzionale all'induttanza della bobina. Maggiore è l'area della bobina, maggiore sarà l'induttanza.
Numero di giri
Con il numero di giri, la bobina influenza direttamente l'induttanza. Il valore dell'induttanza diventa quadrato al numero di spire della bobina. Quindi maggiore è il numero di spire, quadrato di esso sarà il valore dell'induttanza della bobina.
Permeabilità del nucleo
Il permeability (μ)del materiale del nucleo dell'induttore indica il supporto che il nucleo fornisce per la formazione di un campo magnetico al suo interno. Ilhigher la permeabilità del materiale di base, il higher sarà l'induttanza.
Coefficiente di accoppiamento
Questo è un fattore importante da conoscere per il calcolo dell'induttanza reciproca di due bobine. Consideriamo rispettivamente due spire vicine di N1 e N2.
La corrente che attraversa la prima bobina i 1 produce un flusso Ψ 1 . La quantità di collegamenti di flusso magnetico è compresa dalle svolte weber.
Lasciare la quantità di flusso magnetico collegamento alla seconda bobina, a causa della corrente unità di i 1 BE
$$ \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Questo può essere inteso come il coefficiente di mutua induttanza, il che significa
$$ M \: \: = \: \: \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Quindi il coefficiente di induttanza reciproca tra due bobine o circuiti è inteso come il weber si trasforma in una bobina a causa di 1A di corrente nell'altra bobina.
Se l'autoinduttanza della prima bobina è L 1 , allora
$$ L_ {1} i_ {1} \: \: = \: \: {N_ {1} \ varphi_ {1}} \: \: => \: \: \ frac {L_ {1}} {N_ {1}} \: \: \ frac {\ varphi_ {1}} {i_ {1}} $$
$$ M \: \: = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} $$
Allo stesso modo, il coefficiente di mutua induttanza dovuta alla corrente i 2 nella seconda bobina è
$$ M \: \: = \: \: \ frac {N_ {1} \ varphi_ {2}} {i_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \ : 1 $$
Se l'autoinduttanza della seconda bobina è L 2
$$ L_ {2} i_ {2} \: \: = \: \: N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \: \: = \: \: \ frac {\ varphi_ {2}} {i_ {2}} $$
Perciò,
$$ M \: \: = \: \: \ frac {N_ {1} L_ {2}} {N_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \: 2 $$
Moltiplicando 1 e 2, otteniamo
$$ M \: \: \ times \: \: M = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} \: \: \ times \: \: \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ M ^ {2} \: \: = \: \: L_ {1} L_ {2} \: \: => \: \: M \: \: = \: \: \ sqrt {L_ {1 } L_ {2}} $$
L'equazione di cui sopra è vera quando l'intero flusso mutevole della bobina primaria si collega con la bobina secondaria, che è un caso ideale. Ma in pratica non è così. Quindi, possiamo scrivere come
$$ M \: \: \ neq \: \: \ sqrt {L_ {1} L_ {2}} $$
$$ e \ frac {M} {\ sqrt {L_ {1} L_ {2}}} \: \: = \: \: K \: \: \ neq \: \: 1 $$
Dove K è noto come coefficiente di accoppiamento.
Il Coefficient of coupling K può essere definito come il rapporto tra il coefficiente effettivo di mutua induttanza e il coefficiente ideale (massimo) di mutua induttanza.
Se il valore di k è vicino all'unità, allora si dice che le bobine sono strettamente accoppiate e se il valore di k = 0, allora le bobine si dice che siano accoppiate in modo lasco.
Applicazioni degli induttori
Esistono molte applicazioni degli induttori, come:
Gli induttori vengono utilizzati nei circuiti del filtro per rilevare i componenti ad alta frequenza e sopprimere i segnali di rumore
Per isolare il circuito da segnali HF indesiderati.
Gli induttori sono utilizzati nei circuiti elettrici per formare un trasformatore e isolare i circuiti dai picchi.
Gli induttori sono utilizzati anche nei motori.