Elaborazione del segnale digitale - Guida rapida

Definizione

Tutto ciò che trasporta informazioni può essere chiamato come segnale. Può anche essere definita come una grandezza fisica che varia con il tempo, la temperatura, la pressione o con qualsiasi variabile indipendente come il segnale vocale o il segnale video.

Il processo di funzionamento in cui le caratteristiche di un segnale (ampiezza, forma, fase, frequenza, ecc.) Subiscono un cambiamento è noto come elaborazione del segnale.

Note- Qualsiasi segnale indesiderato che interferisce con il segnale principale viene definito rumore. Quindi, anche il rumore è un segnale ma non desiderato.

In base alla loro rappresentazione ed elaborazione, i segnali possono essere classificati in varie categorie, i cui dettagli sono discussi di seguito.

Segnali temporali continui

I segnali a tempo continuo sono definiti lungo un continuum di tempo e sono quindi rappresentati da una variabile continua indipendente. I segnali a tempo continuo vengono spesso definiti segnali analogici.

Questo tipo di segnale mostra continuità sia in ampiezza che in tempo. Questi avranno valori in ogni istante di tempo. Le funzioni seno e coseno sono il miglior esempio di segnale orario continuo.

Il segnale mostrato sopra è un esempio di segnale temporale continuo perché possiamo ottenere il valore del segnale in ogni istante di tempo.

Segnali temporali discreti

I segnali, che sono definiti a tempi discreti, sono noti come segnali discreti. Pertanto, ogni variabile indipendente ha un valore distinto. Pertanto, sono rappresentati come sequenza di numeri.

Sebbene i segnali vocali e video abbiano il privilegio di essere rappresentati sia in formato temporale continuo che discreto; in determinate circostanze, sono identici. Le ampiezze mostrano anche caratteristiche discrete. Un perfetto esempio di ciò è un segnale digitale; la cui ampiezza e tempo sono entrambi discreti.

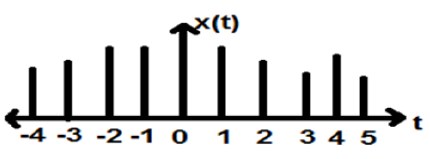
La figura sopra mostra la caratteristica di ampiezza discreta di un segnale discreto in un periodo di tempo. Matematicamente, questi tipi di segnali possono essere formulati come;

$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$

Dove, n è un numero intero.

È una sequenza di numeri x, dove n- ^esimo numero nella sequenza è rappresentato come x [n].

Per testare un sistema, generalmente, vengono utilizzati segnali standard o di base. Questi segnali sono gli elementi costitutivi di base di molti segnali complessi. Quindi, svolgono un ruolo molto importante nello studio di segnali e sistemi.

Impulso unità o funzione delta

Un segnale, che soddisfa la condizione, $\delta(t) = \lim_{\epsilon \to \infty} x(t)$è noto come segnale di impulso unitario. Questo segnale tende all'infinito quando t = 0 e tende a zero quando t ≠ 0 tale che l'area sotto la sua curva è sempre uguale a uno. La funzione delta ha ampiezza zero ovunque excunit_impulse.jpgept at = 0.

Proprietà del segnale di impulso dell'unità

• δ (t) è un segnale uniforme.
• δ (t) è un esempio di segnale né energia né potenza (NENP).
• L'area del segnale di impulso dell'unità può essere scritta come;
$$A = \int_{-\infty}^{\infty} \delta (t)dt = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} x(t) dt = \lim_{\epsilon \to 0} \int_{-\infty}^{\infty} [x(t)dt] = 1$$
• Il peso o la forza del segnale possono essere scritti come;
$$y(t) = A\delta (t)$$
• L'area del segnale di impulso ponderato può essere scritta come:
$$y (t) = \int_{-\infty}^{\infty} y (t)dt = \int_{-\infty}^{\infty} A\delta (t) = A[\int_{-\infty}^{\infty} \delta (t)dt ] = A = 1 = Wigthedimpulse$$

Segnale di passo dell'unità

Un segnale, che soddisfa le seguenti due condizioni:

• $U(t) = 1(when\quad t \geq 0 )and$
• $U(t) = 0 (when\quad t < 0 )$

è noto come segnale di passo unitario.

Ha la proprietà di mostrare discontinuità at = 0. Nel punto di discontinuità, il valore del segnale è dato dalla media del valore del segnale. Questo segnale è stato preso subito prima e dopo il punto di discontinuità (secondo i fenomeni di Gibb).

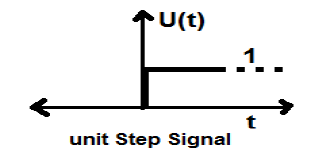
Se aggiungiamo un segnale graduale a un altro segnale graduale scalato nel tempo, il risultato sarà l'unità. È un segnale del tipo di alimentazione e il valore della potenza è 0,5. Il valore RMS (Root mean square) è 0,707 e anche il suo valore medio è 0,5

Segnale di rampa

L'integrazione del segnale di gradino produce un segnale di rampa. È rappresentato da r (t). Anche il segnale di rampa soddisfa la condizione$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$. Non è un segnale di tipo energia né potenza (NENP).

Segnale parabolico

L'integrazione del segnale Ramp porta al segnale parabolico. È rappresentato da p (t). Il segnale parabolico soddisfa anche la condizione$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$. Non è un segnale di tipo Energy né Power (NENP).

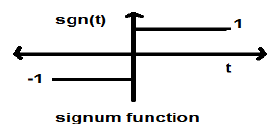
Funzione Signum

Questa funzione è rappresentata come

$$sgn(t) = \begin{cases}1 & for\quad t >0\\-1 & for\quad t<0\end{cases}$$

È un segnale del tipo di alimentazione. Il suo valore di potenza e il valore RMS (Root mean square) sono entrambi 1. Il valore medio della funzione signum è zero.

Funzione Sinc

È anche una funzione del seno ed è scritto come:

$$SinC(t) = \frac{Sin\Pi t}{\Pi T} = Sa(\Pi t)$$

Proprietà della funzione Sinc

• È un segnale di tipo energetico.

• $Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$

• $Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$ (L'intervallo di sinπ∞ varia da -1 a +1 ma qualsiasi cosa divisa per infinito è uguale a zero)

• Se $ \sin c(t) = 0 => \sin \Pi t = 0$

  $\Rightarrow \Pi t = n\Pi$

  $\Rightarrow t = n (n \neq 0)$

Segnale sinusoidale

Un segnale di natura continua è noto come segnale continuo. Il formato generale di un segnale sinusoidale è

$$x(t) = A\sin (\omega t + \phi )$$

Qui,

A = ampiezza del segnale

ω = Frequenza angolare del segnale (misurata in radianti)

φ = Angolo di fase del segnale (misurato in radianti)

La tendenza di questo segnale è di ripetersi dopo un certo periodo di tempo, quindi è chiamato segnale periodico. Il periodo di tempo del segnale è dato come;

$$T = \frac{2\pi }{\omega }$$

Di seguito è mostrata la vista schematica del segnale sinusoidale.

Funzione rettangolare

Si dice che un segnale sia di tipo funzione rettangolare se soddisfa la seguente condizione:

$$\pi(\frac{t}{\tau}) = \begin{cases}1, & for\quad t\leq \frac{\tau}{2}\\0, & Otherwise\end{cases}$$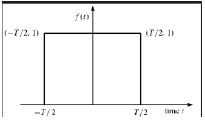

Essendo simmetrico rispetto all'asse Y, questo segnale è definito come segnale uniforme.

Segnale di impulso triangolare

Qualsiasi segnale, che soddisfa la seguente condizione, è noto come segnale triangolare.

$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & for|t|<\frac{\tau}{2}\\0 & for|t|>\frac{\tau}{2}\end{cases}$$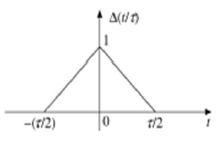

Questo segnale è simmetrico rispetto all'asse Y. Quindi, è anche definito come segnale uniforme.

Abbiamo visto come i segnali di base possono essere rappresentati nel dominio del tempo continuo. Vediamo come i segnali di base possono essere rappresentati nel Discrete Time Domain.

Sequenza di impulsi dell'unità

È indicato come δ (n) nel dominio del tempo discreto e può essere definito come;

$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$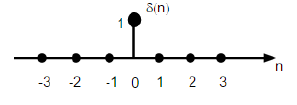

Segnale di passo dell'unità

Il segnale graduale dell'unità di tempo discreto è definito come;

$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$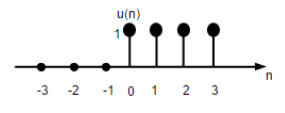

La figura sopra mostra la rappresentazione grafica di una funzione passo discreto.

Funzione di rampa dell'unità

Una funzione di rampa di unità discreta può essere definita come:

$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$

La figura sopra mostra la rappresentazione grafica di un segnale di rampa discreto.

Funzione parabolica

La funzione parabolica dell'unità discreta è indicata come p (n) e può essere definita come;

$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$

In termini di funzione di passo unitario può essere scritto come;

$$P(n) = \frac{n^{2}}{2}U(n)$$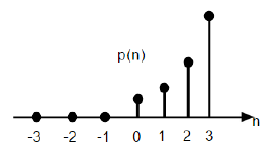

La figura sopra mostra la rappresentazione grafica di una sequenza parabolica.

Segnale sinusoidale

Tutti i segnali a tempo continuo sono periodici. Le sequenze sinusoidali a tempo discreto possono o non possono essere periodiche. Dipendono dal valore di ω. Perché un segnale temporale discreto sia periodico, la frequenza angolare ω deve essere un multiplo razionale di 2π.

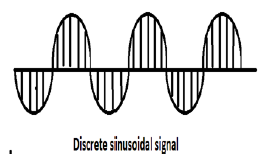
Un segnale sinusoidale discreto è mostrato nella figura sopra.

La forma discreta di un segnale sinusoidale può essere rappresentata nel formato -

$$x(n) = A\sin(\omega n + \phi)$$

Qui A, ω e φ hanno il loro significato usuale e n è l'intero. Il periodo di tempo del segnale sinusoidale discreto è dato da -

$$N =\frac{2\pi m}{\omega}$$

Dove, N e m sono numeri interi.

I segnali temporali continui possono essere classificati in base a diverse condizioni o operazioni eseguite sui segnali.

Segnali pari e dispari

Even Signal

Si dice che un segnale sia anche se soddisfa la seguente condizione;

$$x(-t) = x(t)$$

L'inversione del tempo del segnale non implica alcuna variazione dell'ampiezza qui. Ad esempio, considera l'onda triangolare mostrata di seguito.

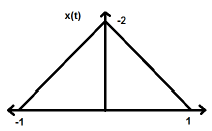
Il segnale triangolare è un segnale uniforme. Poiché è simmetrico rispetto all'asse Y. Possiamo dire che è un'immagine speculare sull'asse Y.

Considera un altro segnale come mostrato nella figura sotto.

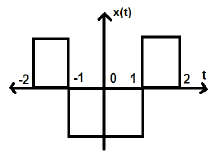
Possiamo vedere che il segnale di cui sopra è uniforme poiché è simmetrico rispetto all'asse Y.

Segnale strano

Si dice che un segnale sia strano se soddisfa la seguente condizione

$$x(-t) = -x(t)$$

Qui, sia l'inversione del tempo che il cambio di ampiezza avvengono simultaneamente.

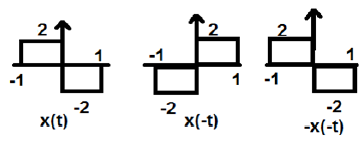
Nella figura sopra, possiamo vedere un segnale di gradino x (t). Per verificare se si tratta di un segnale dispari o meno, prima eseguiamo l'inversione temporale, cioè x (-t) e il risultato è come mostrato in figura. Quindi invertiamo l'ampiezza del segnale risultante cioè –x (-t) e otteniamo il risultato come mostrato in figura.

Se confrontiamo la prima e la terza forma d'onda, possiamo vedere che sono uguali, cioè x (t) = -x (-t), che soddisfa i nostri criteri. Pertanto, il segnale di cui sopra è un segnale dispari.

Di seguito vengono forniti alcuni risultati importanti relativi ai segnali pari e dispari.

• Pari × Pari = Pari
• Dispari × Dispari = Pari
• Pari × Dispari = Dispari
• Pari ± Pari = Pari
• Dispari ± Dispari = Dispari
• Pari ± Dispari = Né pari né dispari

Rappresentazione di qualsiasi segnale in forma pari o dispari

Alcuni segnali non possono essere classificati direttamente in tipo pari o dispari. Questi sono rappresentati come una combinazione di segnali pari e dispari.

$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$

Dove x _e (t) rappresenta il segnale pari e x _o (t) rappresenta il segnale dispari

$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$

E

$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$

Esempio

Trova le parti pari e dispari del segnale $x(n) = t+t^{2}+t^{3}$

Solution - Dall'inversione di x (n), otteniamo

$$x(-n) = -t+t^{2}-t^{3}$$

Ora, secondo la formula, la parte pari

$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$

$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$

$$= t^{2}$$

Allo stesso modo, secondo la formula la parte dispari è

$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$

$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$

$$= t+t^{3}$$

Segnali periodici e non periodici

Segnali periodici

Il segnale periodico si ripete dopo un certo intervallo di tempo. Possiamo mostrarlo in forma di equazione come -

$$x(t) = x(t)\pm nT$$

Dove, n = un numero intero (1,2,3 ……)

T = periodo di tempo fondamentale (FTP) ≠ 0 e ≠ ∞

Il periodo di tempo fondamentale (FTP) è il più piccolo valore di tempo positivo e fisso per il quale il segnale è periodico.

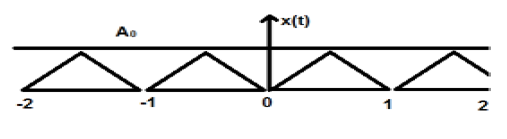
Un segnale triangolare è mostrato nella figura sopra di ampiezza A. Qui, il segnale si ripete ogni 1 sec. Pertanto, possiamo dire che il segnale è periodico e il suo FTP è di 1 sec.

Segnale non periodico

Semplicemente, possiamo dire, i segnali, che non sono periodici, sono di natura non periodica. Come ovvio, questi segnali non si ripetono dopo alcun intervallo di tempo.

I segnali non periodici non seguono un certo formato; pertanto nessuna equazione matematica particolare può descriverli.

Segnali di energia e potenza

Si dice che un segnale sia un segnale di Energia, se e solo se l'energia totale contenuta è finita e diversa da zero (0 <E <∞). Pertanto, per qualsiasi segnale di tipo energetico, il segnale normalizzato totale è finito e diverso da zero.

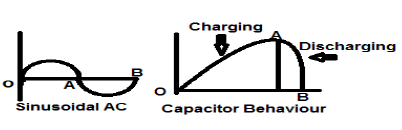
Un segnale di corrente CA sinusoidale è un perfetto esempio di segnale di tipo Energy perché è in un mezzo ciclo positivo in un caso e poi è negativo nel mezzo ciclo successivo. Pertanto, la sua potenza media diventa zero.

Un condensatore lossless è anche un perfetto esempio di segnale di tipo Energy perché quando è collegato a una sorgente si carica fino al suo livello ottimale e quando la sorgente viene rimossa, dissipa quella stessa quantità di energia attraverso un carico e rende la sua potenza media a zero.

Per ogni segnale finito x (t) l'energia può essere simbolizzata come E ed è scritta come;

$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$

La densità spettrale dei segnali di tipo energetico fornisce la quantità di energia distribuita a vari livelli di frequenza.

Segnali di tipo di alimentazione

Si dice che un segnale sia un segnale del tipo di potenza, se e solo se, la potenza media normalizzata è finita e diversa da zero cioè (0 <p <∞). Per il segnale di tipo power, la potenza media normalizzata è finita e diversa da zero. Quasi tutti i segnali periodici sono segnali di potenza e la loro potenza media è finita e diversa da zero.

In forma matematica, la potenza di un segnale x (t) può essere scritta come;

$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$

Differenza tra segnali di energia e potenza

La tabella seguente riassume le differenze dei segnali di energia e potenza.

Segnale di potenza	Segnale di energia
I segnali periodici pratici sono segnali di potenza.	I segnali non periodici sono segnali energetici.
Qui, la potenza media normalizzata è finita e diversa da zero.	Qui, l'energia totale normalizzata è finita e diversa da zero.
Matematicamente, $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$	Matematicamente, $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$
L'esistenza di questi segnali è infinita nel tempo.	Questi segnali esistono per un periodo di tempo limitato.
L'energia del segnale di potenza è infinita nel tempo infinito.	La potenza del segnale energetico è zero nel tempo infinito.

Esempi risolti

Example 1 - Trova la potenza di un segnale $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$

Solution- I due segnali di cui sopra sono ortogonali tra loro perché i loro termini di frequenza sono identici tra loro, inoltre hanno la stessa differenza di fase. Quindi, il potere totale sarà la somma dei poteri individuali.

Permettere $z(t) = x(t)+y(t)$

Dove $x(t) = 2\cos (3\Pi t+30^{o})$ e $y(t) = 4\sin(3\Pi +30^{o})$

Potere di $x(t) = \frac{2^{2}}{2} = 2$

Potere di $y(t) = \frac{4^{2}}{2} = 8$

Perciò, $P(z) = p(x)+p(y) = 2+8 = 10$... Ans.

Example 2 - Verifica se il segnale fornito $x(t) = t^{2}+j\sin t$ è coniugato o no?

Solution- Qui, la parte reale che è t ² è la parte pari e dispari (immaginario)$\sin t$è strano. Quindi il segnale di cui sopra è il segnale coniugato.

Example 3 - Verifica se $X(t)= \sin \omega t$ è un segnale dispari o un segnale pari.

Solution - Dato $X(t) = \sin \omega t$

Con l'inversione del tempo, otterremo $\sin (-\omega t)$

Ma questo lo sappiamo $\sin(-\phi) = -\sin \phi$.

Perciò,

$$\sin (-\omega t) = -\sin \omega t$$

Ciò soddisfa la condizione affinché un segnale sia dispari. Perciò,$\sin \omega t$ è un segnale strano.

Proprio come i segnali temporali continui, i segnali temporali discreti possono essere classificati in base alle condizioni o alle operazioni sui segnali.

Segnali pari e dispari

Even Signal

Un segnale si dice pari o simmetrico se soddisfa la seguente condizione;

$$x(-n) = x(n)$$

Qui possiamo vedere che x (-1) = x (1), x (-2) = x (2) e x (-n) = x (n). Quindi, è un segnale uniforme.

Segnale strano

Un segnale si dice strano se soddisfa la seguente condizione;

$$x(-n) = -x(n)$$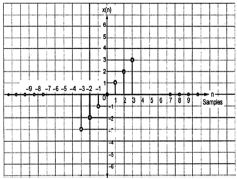

Dalla figura possiamo vedere che x (1) = -x (-1), x (2) = -x (2) e x (n) = -x (-n). Quindi, è un segnale strano e antisimmetrico.

Segnali periodici e non periodici

Un segnale orario discreto è periodico se e solo se soddisfa la seguente condizione:

$$x(n+N) = x(n)$$

Qui, il segnale x (n) si ripete dopo N periodo. Questo può essere meglio compreso considerando un segnale coseno -

$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$

Affinché il segnale diventi periodico, deve essere soddisfatta la seguente condizione;

$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$

cioè $2\pi f_{0}N$ è un multiplo integrale di $2\pi$

$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$

Le frequenze dei segnali sinusoidali discreti sono separate dal multiplo integrale di $2\pi$.

Segnali di energia e potenza

Segnale di energia

L'energia di un segnale temporale discreto è indicata come E. Matematicamente, può essere scritta come;

$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$

Se ogni singolo valore di $x(n)$sono al quadrato e sommati, otteniamo il segnale di energia. Qui$x(n)$ è il segnale di energia e la sua energia è finita nel tempo, cioè $ 0 <E <\ infty $

Segnale di alimentazione

La potenza media di un segnale discreto è rappresentata come P. Matematicamente, questo può essere scritto come;

$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$

Qui, la potenza è finita, cioè 0 <P <∞. Tuttavia, ci sono alcuni segnali, che non appartengono né a un segnale di tipo energia né a potenza.

Ci sono altri segnali, che sono il risultato dell'operazione eseguita su di essi. Alcuni tipi comuni di segnali sono discussi di seguito.

Segnali coniugati

Segnali, che soddisfano la condizione $x(t) = x*(-t)$ sono chiamati segnali coniugati.

Permettere $x(t) = a(t)+jb(t)$... eqn. 1

Così, $x(-t) = a(-t)+jb(-t)$

E $x*(-t) = a(-t)-jb(-t)$... eqn. 2

Per condizione, $x(t) = x*(-t)$

Se confrontiamo entrambe le equazioni derivate 1 e 2, possiamo vedere che la parte reale è pari, mentre la parte immaginaria è dispari. Questa è la condizione affinché un segnale sia di tipo coniugato.

Segnali antisimmetrici coniugati

Segnali che soddisfano la condizione $x(t) = -x*(-t)$ sono chiamati segnali antisimmetrici coniugati

Permettere $x(t) = a(t)+jb(t)$... eqn. 1

Così $x(-t) = a(-t)+jb(-t)$

E $x*(-t) = a(-t)-jb(-t)$

$-x*(-t) = -a(-t)+jb(-t)$... eqn. 2

Per condizione $x(t) = -x*(-t)$

Ora, confronta di nuovo entrambe le equazioni proprio come abbiamo fatto per i segnali coniugati. Qui scopriremo che la parte reale è strana e la parte immaginaria è pari. Questa è la condizione perché un segnale diventi di tipo antisimmetrico coniugato.

Esempio

Lascia che sia il segnale dato $x(t) = \sin t+jt^{2}$.

Qui, la parte reale è $\sin t$ è strano e la parte immaginaria è $t^2$è anche. Quindi, questo segnale può essere classificato come segnale antisimmetrico coniugato.

Ogni funzione può essere divisa in due parti. Una parte è coniugata simmetria e l'altra parte è coniugata antisimmetrica. Quindi qualsiasi segnale x (t) può essere scritto come

$$x(t) = xcs(t)+xcas(t)$$

Dove $xcs(t)$ è il segnale simmetrico coniugato e $xcas(t)$ è un segnale anti simmetrico coniugato

$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$

E

$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$

Segnali simmetrici a mezza onda

Quando un segnale soddisfa la condizione $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$, è chiamato segnale simmetrico a semionda. In questo caso, l'inversione di ampiezza e lo spostamento temporale del segnale avvengono a metà tempo. Per il segnale simmetrico a semionda, il valore medio sarà zero ma questo non è il caso quando la situazione è invertita.

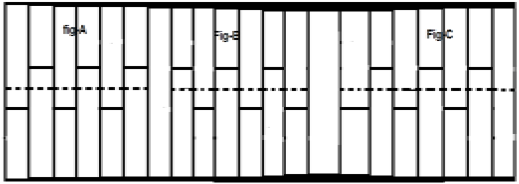
Considera un segnale x (t) come mostrato nella figura A sopra. Il primo passo è spostare il segnale nel tempo e farlo$x[t-(\frac{T}{2})]$. Quindi, il nuovo segnale viene modificato come mostrato nella figura B. Successivamente, invertiamo l'ampiezza del segnale, cioè lo facciamo$-x[t-(\frac{T}{2})]$ come mostrato nella figura C. Poiché questo segnale si ripete dopo lo spostamento a metà tempo e l'inversione di ampiezza, è un segnale simmetrico a semionda.

Segnale ortogonale

Si dice che due segnali x (t) e y (t) siano ortogonali se soddisfano le seguenti due condizioni.

Condition 1 - $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [per segnale non periodico]

Condition 2 - $\int x(t)y(t) = 0$ [Per segnale periodico]

I segnali che contengono armoniche dispari (3 ^rd , 5 ^th , 7 ^th ... ecc.) Ed hanno differenti frequenze, sono reciprocamente ortogonali fra loro.

Nei segnali di tipo trigonometrico, anche le funzioni seno e coseno sono ortogonali tra loro; purché abbiano la stessa frequenza e siano nella stessa fase. Allo stesso modo anche i segnali DC (segnali in corrente continua) e sinusoidali sono ortogonali tra loro. Se x (t) ey (t) sono due segnali ortogonali e$z(t) = x(t)+y(t)$ quindi la potenza e l'energia di z (t) possono essere scritte come;

$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$

Esempio

Analizza il segnale: $z(t) = 3+4\sin(2\pi t+30^0)$

Qui, il segnale comprende un segnale DC (3) e una funzione seno. Quindi, per proprietà questo segnale è un segnale ortogonale ei due sottosegnali in esso sono mutuamente ortogonali tra loro.

Spostamento significa movimento del segnale, nel dominio del tempo (attorno all'asse Y) o nel dominio dell'ampiezza (attorno all'asse X). Di conseguenza, possiamo classificare lo spostamento in due categorie denominate Spostamento del tempo e Spostamento dell'ampiezza, che vengono successivamente discusse di seguito.

Tempo di spostamento

Time shifting significa spostamento dei segnali nel dominio del tempo. Matematicamente, può essere scritto come

$$x(t) \rightarrow y(t+k)$$

Questo valore K può essere positivo o negativo. In base al segno del valore k, abbiamo due tipi di spostamento denominati spostamento a destra e spostamento a sinistra.

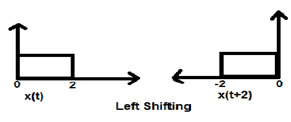
Caso 1 (K> 0)

Quando K è maggiore di zero, lo spostamento del segnale avviene verso "sinistra" nel dominio del tempo. Pertanto, questo tipo di spostamento è noto come spostamento a sinistra del segnale.

Example

Caso 2 (K <0)

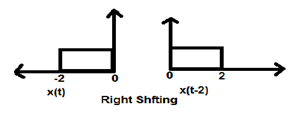
Quando K è minore di zero, lo spostamento del segnale avviene verso destra nel dominio del tempo. Pertanto, questo tipo di spostamento è noto come spostamento a destra.

Example

La figura sotto mostra lo spostamento a destra di un segnale di 2.

Variazione dell'ampiezza

Spostamento di ampiezza significa spostamento del segnale nel dominio dell'ampiezza (attorno all'asse X). Matematicamente, può essere rappresentato come:

$$x(t) \rightarrow x(t)+K$$

Questo valore K può essere positivo o negativo. Di conseguenza, abbiamo due tipi di spostamento di ampiezza che vengono successivamente discussi di seguito.

Caso 1 (K> 0)

Quando K è maggiore di zero, lo spostamento del segnale avviene verso l'alto nell'asse x. Pertanto, questo tipo di spostamento è noto come spostamento verso l'alto.

Example

Consideriamo un segnale x (t) che è dato come;

$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

Abbiamo preso K = + 1 in modo che il nuovo segnale possa essere scritto come -

$y(t) \rightarrow x(t)+1$ Quindi, y (t) può finalmente essere scritto come;

$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$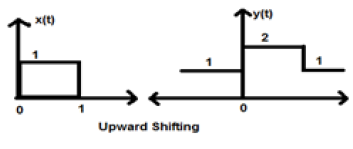

Caso 2 (K <0)

Quando K è minore di zero, lo spostamento del segnale avviene verso il basso nell'asse X. Pertanto, è chiamato spostamento verso il basso del segnale.

Example

Consideriamo un segnale x (t) che è dato come;

$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

Abbiamo preso K = -1 in modo che il nuovo segnale possa essere scritto come;

$y(t)\rightarrow x(t)-1$ Quindi, y (t) può finalmente essere scritto come;

$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$

Scalare un segnale significa che una costante viene moltiplicata per il tempo o l'ampiezza del segnale.

Scala temporale

Se una costante viene moltiplicata per l'asse del tempo, è nota come scala temporale. Questo può essere rappresentato matematicamente come;

$x(t) \rightarrow y(t) = x(\alpha t)$ o $x(\frac{t}{\alpha})$; dove α ≠ 0

Quindi, essendo l'asse y stesso, l'intensità dell'asse x diminuisce o aumenta in base al segno della costante (sia positiva che negativa). Pertanto, il ridimensionamento può anche essere suddiviso in due categorie come discusso di seguito.

Compressione del tempo

Ogni volta che alfa è maggiore di zero, l'ampiezza del segnale viene divisa per alfa mentre il valore dell'asse Y rimane lo stesso. Questo è noto come compressione temporale.

Example

Consideriamo un segnale x (t), che è mostrato come nella figura sotto. Prendiamo il valore di alfa come 2. Quindi, y (t) sarà x (2t), come illustrato nella figura data.

Chiaramente, possiamo vedere dalle figure precedenti che l'ampiezza temporale sull'asse y rimane la stessa ma l'ampiezza sull'asse x si riduce da 4 a 2. Pertanto, è un caso di compressione temporale.

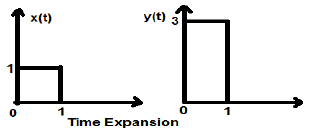
Espansione del tempo

Quando il tempo viene diviso per la costante alfa, l'ampiezza dell'asse Y del segnale viene moltiplicata per alfa volte, mantenendo l'ampiezza dell'asse X così com'è. Pertanto, questo è chiamato segnale del tipo di espansione temporale.

Example

Consideriamo un segnale quadrato x (t), di magnitudine 1. Quando lo abbiamo scalato nel tempo di una costante 3, in modo tale che $x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$, quindi l'ampiezza del segnale viene modificata di 3 volte, come mostrato nella figura sotto.

Scala dell'ampiezza

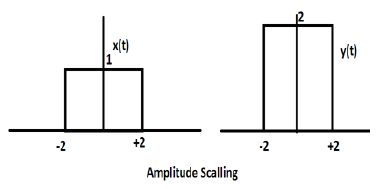
La moltiplicazione di una costante per l'ampiezza del segnale causa un ridimensionamento dell'ampiezza. A seconda del segno della costante, può trattarsi di ridimensionamento o attenuazione dell'ampiezza. Consideriamo un segnale ad onda quadra x (t) = Π (t / 4).

Supponiamo di definire un'altra funzione y (t) = 2 Π (t / 4). In questo caso, il valore dell'asse y sarà raddoppiato, mantenendo il valore dell'asse temporale così com'è. Il è illustrato nella figura sotto riportata.

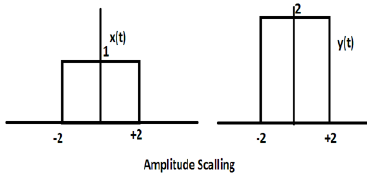
Considera un'altra funzione d'onda quadra definita come z (t) dove z (t) = 0,5 Π (t / 4). Qui, l'ampiezza della funzione z (t) sarà la metà di quella di x (t), cioè l'asse del tempo rimanendo lo stesso, l'asse dell'ampiezza sarà dimezzato. Ciò è illustrato dalla figura riportata di seguito.

Ogni volta che il tempo in un segnale viene moltiplicato per -1, il segnale viene invertito. Produce la sua immagine speculare sull'asse Y o X. Questo è noto come inversione del segnale.

L'inversione può essere classificata in due tipi in base alla condizione se il tempo o l'ampiezza del segnale vengono moltiplicati per -1.

Inversione temporale

Ogni volta che il tempo del segnale viene moltiplicato per -1, è noto come inversione temporale del segnale. In questo caso, il segnale produce la sua immagine speculare attorno all'asse Y. Matematicamente, questo può essere scritto come;

$$x(t) \rightarrow y(t) \rightarrow x(-t)$$

Questo può essere meglio compreso dal seguente esempio.

Nell'esempio sopra, possiamo vedere chiaramente che il segnale è stato invertito attorno al suo asse Y. Quindi, è anche un tipo di scala temporale, ma qui la quantità di scala è sempre (-1).

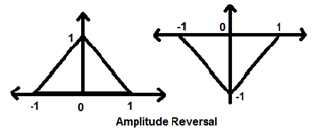
Inversione di ampiezza

Ogni volta che l'ampiezza di un segnale viene moltiplicata per -1, si parla di inversione di ampiezza. In questo caso, il segnale produce la sua immagine speculare attorno all'asse X. Matematicamente, questo può essere scritto come;

$$x(t)\rightarrow y(t)\rightarrow -x(t)$$

Considera il seguente esempio. L'inversione di ampiezza può essere vista chiaramente.

Due operazioni molto importanti eseguite sui segnali sono la differenziazione e l'integrazione.

Differenziazione

Differenziazione di qualsiasi segnale x (t) significa rappresentazione della pendenza di quel segnale rispetto al tempo. Matematicamente, è rappresentato come;

$$x(t)\rightarrow \frac{dx(t)}{dt}$$

Nel caso della differenziazione OPAMP, questa metodologia è molto utile. Possiamo facilmente differenziare un segnale graficamente piuttosto che usare la formula. Tuttavia, la condizione è che il segnale debba essere di tipo rettangolare o triangolare, cosa che accade nella maggior parte dei casi.

Segnale originale	Segnale differenziato
Rampa	Passo
Passo	Impulso
Impulso	1

La tabella sopra mostra la condizione del segnale dopo essere stato differenziato. Ad esempio, un segnale di rampa si converte in un segnale di gradino dopo la differenziazione. Allo stesso modo, un segnale di passo unitario diventa un segnale di impulso.

Esempio

Lascia che sia il segnale che ci viene dato $x(t) = 4[r(t)-r(t-2)]$. Quando questo segnale viene tracciato, apparirà come quello sul lato sinistro della figura sotto riportata. Ora, il nostro scopo è differenziare il segnale dato.

Per cominciare, inizieremo a differenziare l'equazione data. Sappiamo che il segnale di rampa dopo la differenziazione fornisce un segnale di passo unitario.

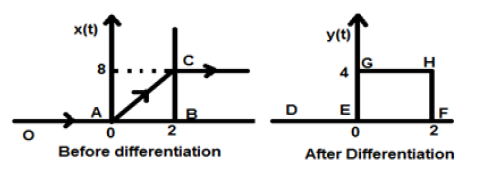
Quindi il nostro segnale risultante y (t) può essere scritto come;

$y(t) = \frac{dx(t)}{dt}$

$= \frac{d4[r(t)-r(t-2)]}{dt}$

$= 4[u(t)-u(t-2)]$

Ora questo segnale è finalmente tracciato, che è mostrato nella parte destra della figura sopra.

L'integrazione di qualsiasi segnale significa la somma di quel segnale in un particolare dominio del tempo per ottenere un segnale modificato. Matematicamente, questo può essere rappresentato come:

$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$

Anche qui, nella maggior parte dei casi, possiamo fare l'integrazione matematica e trovare il segnale risultante, ma l'integrazione diretta in rapida successione è possibile per i segnali che sono rappresentati graficamente in formato rettangolare. Come per la differenziazione, anche qui faremo riferimento a una tabella per ottenere rapidamente il risultato.

Segnale originale	Segnale integrato
1	impulso
Impulso	passo
Passo	Rampa

Esempio

Consideriamo un segnale $x(t) = u(t)-u(t-3)$. È mostrato in Fig-1 sotto. Chiaramente, possiamo vedere che è un segnale di passo. Ora lo integreremo. Facendo riferimento alla tabella, sappiamo che l'integrazione del segnale di gradino produce un segnale di rampa.

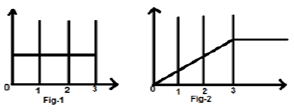
Tuttavia, lo calcoleremo matematicamente,

$y(t) = \int_{-\infty}^{t}x(t)dt$

$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$

$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$

$= r(t)-r(t-3)$

Lo stesso è tracciato come mostrato in fig-2,

La convoluzione di due segnali nel dominio del tempo è equivalente alla moltiplicazione della loro rappresentazione nel dominio della frequenza. Matematicamente, possiamo scrivere la convoluzione di due segnali come

$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$

Passaggi per la convoluzione

• Prendi il segnale x ₁ (t) e metti t = p in modo che sia x ₁ (p).
• Prendi il segnale x ₂ (t) e fai il passaggio 1 e rendilo x ₂ (p).
• Effettua il ripiegamento del segnale cioè x ₂ (-p).
• Effettua lo spostamento temporale del segnale precedente x ₂ [- (pt)]
• Quindi fai la moltiplicazione di entrambi i segnali. cioè$x_{1}(p).x_{2}[−(p−t)]$

Esempio

Facciamo la convoluzione di un segnale a gradino u (t) con il suo genere.

$y(t) = u(t)*u(t)$

$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$

Ora questo t può essere maggiore o minore di zero, come mostrato nelle figure seguenti

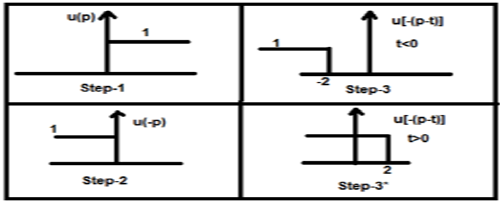
Quindi, con il caso precedente, il risultato si presenta con le seguenti possibilità

$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$

$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$

Proprietà della convoluzione

Commutativo

Afferma che l'ordine di convoluzione non ha importanza, il che può essere mostrato matematicamente come

$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$

Associativo

Afferma che l'ordine di convoluzione che coinvolge tre segnali può essere qualsiasi cosa. Matematicamente, può essere mostrato come;

$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$

Distributivo

Prima possono essere aggiunti due segnali, quindi la loro convoluzione può essere effettuata al terzo segnale. Ciò equivale alla convoluzione di due segnali individualmente con il terzo segnale e alla fine aggiunti. Matematicamente, questo può essere scritto come;

$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$

La zona

Se un segnale è il risultato della convoluzione di due segnali, l'area del segnale è la moltiplicazione di quei segnali individuali. Matematicamente questo può essere scritto

Se $y(t) = x_{1}*x_{2}(t)$

Quindi, Area di y (t) = Area di x ₁ (t) X Area di x ₂ (t)

Ridimensionamento

Se due segnali vengono scalati su una costante sconosciuta "a" e viene eseguita la convoluzione, anche il segnale risultante verrà convoluto alla stessa costante "a" e sarà diviso per quella quantità come mostrato di seguito.

Se, $x_{1}(t)*x_{2}(t) = y(t)$

Poi, $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$

Ritardo

Supponiamo che un segnale y (t) sia il risultato della convoluzione di due segnali x1 (t) e x2 (t). Se i due segnali sono ritardati rispettivamente del tempo t1 e t2, il segnale risultante y (t) sarà ritardato di (t1 + t2). Matematicamente, può essere scritto come -

Se, $x_{1}(t)*x_{2}(t) = y(t)$

Poi, $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$

Esempi risolti

Example 1 - Trova la convoluzione dei segnali u (t-1) eu (t-2).

Solution- I segnali dati sono u (t-1) eu (t-2). La loro convoluzione può essere eseguita come mostrato di seguito:

$y(t) = u(t-1)*u(t-2)$

$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$

$= r(t-1)+r(t-2)$

$= r(t-3)$

Example 2 - Trova la convoluzione di due segnali data da

$x_{1}(n) = \lbrace 3,-2, 2\rbrace $

$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$

Solution -

x ₂ (n) può essere decodificato come$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$

x ₁ (n) è dato in precedenza$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$

Allo stesso modo, $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

Segnale risultante,

$X(Z) = X_{1}(Z)X_{2}(z)$

$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$

Prendendo la trasformazione Z inversa di quanto sopra, otterremo il segnale risultante come

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ Origine al primo

Example 3 - Determina la convoluzione dei seguenti 2 segnali -

$x(n) = \lbrace 2,1,0,1\rbrace$

$h(n) = \lbrace 1,2,3,1\rbrace$

Solution -

Prendendo la trasformazione Z dei segnali, otteniamo,

$x(z) = 2+2Z^{-1}+2Z^{-3}$

E $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$

Ora la convoluzione di due segnali significa moltiplicazione delle loro trasformazioni Z.

Questo è $Y(Z) = X(Z) \times h(Z)$

$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$

$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$

Prendendo la trasformazione Z inversa, il segnale risultante può essere scritto come;

$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$

Alcuni sistemi hanno feedback e altri no. Quelli che non hanno sistemi di feedback, il loro output dipende solo dai valori attuali dell'input. Il valore passato dei dati non è presente in quel momento. Questi tipi di sistemi sono noti come sistemi statici. Non dipende anche dai valori futuri.

Poiché questi sistemi non hanno alcun record passato, quindi non hanno anche alcuna memoria. Pertanto, diciamo che tutti i sistemi statici sono sistemi senza memoria. Facciamo un esempio per capire molto meglio questo concetto.

Esempio

Verifichiamo se i seguenti sistemi sono statici o meno.

• $y(t) = x(t)+x(t-1)$
• $y(t) = x(2t)$
• $y(t) = x = \sin [x(t)]$

un) $y(t) = x(t)+x(t-1)$

Qui, x (t) è il valore attuale. Non ha alcuna relazione con i valori passati del tempo. Quindi, è un sistema statico. Tuttavia, nel caso di x (t-1), se mettiamo t = 0, si ridurrà ax (-1) che dipende da un valore passato. Quindi, non è statico. Quindi qui y (t) non è un sistema statico.

b) $y(t) = x(2t)$

Se sostituiamo t = 2, il risultato sarà y (t) = x (4). Di nuovo, dipende dal valore futuro. Quindi, non è nemmeno un sistema statico.

c) $y(t) = x = \sin [x(t)]$

In questa espressione, abbiamo a che fare con la funzione seno. L'intervallo della funzione seno è compreso tra -1 e +1. Quindi, qualunque siano i valori che sostituiamo per x (t), andremo tra -1 e +1. Pertanto, possiamo dire che non dipende da alcun valore passato o futuro. Quindi, è un sistema statico.

Dagli esempi precedenti, possiamo trarre le seguenti conclusioni:

• Qualsiasi sistema con spostamento del tempo non è statico.
• Anche qualsiasi sistema con spostamento di ampiezza non è statico.
• Anche i casi di integrazione e differenziazione non sono statici.

Se un sistema dipende dal valore passato e futuro del segnale in qualsiasi istante del tempo, allora è noto come sistema dinamico. A differenza dei sistemi statici, questi non sono sistemi senza memoria. Memorizzano valori passati e futuri. Pertanto, richiedono un po 'di memoria. Cerchiamo di comprendere meglio questa teoria attraverso alcuni esempi.

Esempi

Scopri se i seguenti sistemi sono dinamici.

a) $y(t) = x(t+1)$

In questo caso, se mettiamo t = 1 nell'equazione, verrà convertito in x (2), che è un valore dipendente futuro. Perché qui stiamo dando input come 1 ma mostra il valore per x (2). Poiché è un segnale dipendente dal futuro, è chiaro che è un sistema dinamico.

b) $y(t) = Real[x(t)]$

$$= \frac{[x(t)+x(t)^*]}{2}$$

In questo caso, qualunque sia il valore che inseriremo, mostrerà quel segnale del valore reale del tempo. Non dipende da valori futuri o passati. Pertanto, non è un sistema dinamico, piuttosto è un sistema statico.

c) $y(t) = Even[x(t)]$

$$= \frac{[x(t)+x(-t)]}{2}$$

Qui, se sostituiamo t = 1, un segnale mostra x (1) e un altro mostrerà x (-1) che è un valore passato. Allo stesso modo, se mettiamo t = -1, un segnale mostrerà x (-1) e un altro mostrerà x (1) che è un valore futuro. Quindi, chiaramente è un caso di sistema dinamico.

d) $y(t) = \cos [x(t)]$

In questo caso, poiché il sistema è una funzione del coseno, ha un certo dominio di valori compreso tra -1 e +1. Pertanto, qualunque sia il valore che inseriremo, otterremo il risultato entro il limite specificato. Pertanto, è un sistema statico

Dagli esempi precedenti, possiamo trarre le seguenti conclusioni:

• Tutti i segnali dei casi di time shifting sono segnali dinamici.
• Anche in caso di scala temporale, tutti i segnali sono segnali dinamici.
• I segnali dei casi di integrazione sono segnali dinamici.

In precedenza, abbiamo visto che il sistema deve essere indipendente dai valori futuri e passati per diventare statico. In questo caso, la condizione è quasi la stessa con poche modifiche. Qui, affinché il sistema sia causale, dovrebbe essere indipendente solo dai valori futuri. Ciò significa che la dipendenza passata non causerà alcun problema al sistema dal diventare causale.

I sistemi causali sono sistemi realizzabili praticamente o fisicamente. Consideriamo alcuni esempi per capirlo molto meglio.

Esempi

Consideriamo i seguenti segnali.

a) $y(t) = x(t)$

Qui, il segnale dipende solo dai valori attuali di x. Ad esempio, se sostituiamo t = 3, il risultato verrà visualizzato solo per quell'istante di tempo. Pertanto, poiché non ha dipendenza dal valore futuro, possiamo chiamarlo un sistema causale.

b) $y(t) = x(t-1)$

Qui, il sistema dipende dai valori passati. Ad esempio, se sostituiamo t = 3, l'espressione si ridurrà ax (2), che è un valore passato rispetto al nostro input. In nessun caso, dipende da valori futuri. Pertanto, questo sistema è anche un sistema causale.

c) $y(t) = x(t)+x(t+1)$

In questo caso, il sistema ha due parti. La parte x (t), come abbiamo discusso in precedenza, dipende solo dai valori presenti. Quindi, non ci sono problemi con esso. Tuttavia, se prendiamo il caso di x (t + 1), dipende chiaramente dai valori futuri perché se mettiamo t = 1, l'espressione si ridurrà a x (2) che è il valore futuro. Pertanto, non è causale.

Un sistema non causale è esattamente opposto a quello del sistema causale. Se un sistema dipende dai valori futuri dell'input in qualsiasi istante del tempo, si dice che il sistema è un sistema non causale.

Esempi

Facciamo alcuni esempi e cerchiamo di capirlo in modo migliore.

a) $y(t) = x(t+1)$

Abbiamo già discusso questo sistema anche nel sistema causale. Per qualsiasi input, ridurrà il sistema al suo valore futuro. Ad esempio, se mettiamo t = 2, si ridurrà ax (3), che è un valore futuro. Pertanto, il sistema è non causale.

b) $y(t) = x(t)+x(t+2)$

In questo caso, x (t) è puramente una funzione dipendente dal valore attuale. Abbiamo già discusso che la funzione x (t + 2) dipende dal futuro perché per t = 3 darà valori per x (5). Pertanto, non è causale.

c) $y(t) = x(t-1)+x(t)$

In questo sistema, dipende dai valori presenti e passati dell'input fornito. Qualunque siano i valori che sostituiamo, non mostrerà mai alcuna dipendenza futura. Chiaramente, non è un sistema non causale; piuttosto è un sistema causale.

Un sistema anti-causale è solo una versione leggermente modificata di un sistema non causale. Il sistema dipende solo dai valori futuri dell'input. Non ha alcuna dipendenza né dal presente né dai valori passati.

Esempi

Scopri se i seguenti sistemi sono anti-causali.

a) $y(t) = x(t)+x(t-1)$

Il sistema ha due sotto-funzioni. Una sottofunzione x (t + 1) dipende dal valore futuro dell'ingresso, ma un'altra sottofunzione x (t) dipende solo dal presente. Poiché il sistema dipende dal valore presente anche oltre al valore futuro, questo sistema non è anti-causale.

b) $y(t) = x(t+3)$

Se analizziamo il sistema di cui sopra, possiamo vedere che il sistema dipende solo dai valori futuri del sistema, ovvero se mettiamo t = 0, si ridurrà ax (3), che è un valore futuro. Questo sistema è un perfetto esempio di sistema anti-causale.

Un sistema lineare segue le leggi di sovrapposizione. Questa legge è condizione necessaria e sufficiente per dimostrare la linearità del sistema. Oltre a questo, il sistema è una combinazione di due tipi di leggi:

• Legge di additività
• Legge di omogeneità

Sia la legge dell'omogeneità che la legge dell'additività sono mostrate nelle figure precedenti. Tuttavia, esistono altre condizioni per verificare se il sistema è lineare o meno.

The conditions are -

• L'output dovrebbe essere zero per zero input.
• Non dovrebbe essere presente alcun operatore non lineare nel sistema.

Esempi di operatori non lineari -

(a) Operatori trigonometrici: Sin, Cos, Tan, Cot, Sec, Cosec ecc.

(b) Esponenziale, logaritmico, modulo, quadrato, cubo ecc.

(c) sa (i / p), Sinc (i / p), Sqn (i / p) ecc.

Sia l'input x sia l'output y non dovrebbero avere questi operatori non lineari.

Esempi

Cerchiamo di scoprire se i seguenti sistemi sono lineari.

a) $y(t) = x(t)+3$

Questo sistema non è un sistema lineare perché viola la prima condizione. Se mettiamo l'input come zero, rendendo x (t) = 0, allora l'output non è zero.

b) $y(t) = \sin tx(t)$

In questo sistema, se diamo input come zero, l'output diventerà zero. Quindi, la prima condizione è chiaramente soddisfatta. Anche in questo caso, non esiste alcun operatore non lineare applicato a x (t). Quindi, anche la seconda condizione è soddisfatta. Pertanto, il sistema è un sistema lineare.

c) $y(t) = \sin (x(t))$

Nel sistema sopra, la prima condizione è soddisfatta perché se mettiamo x (t) = 0, l'uscita sarà anche sin (0) = 0. Tuttavia, la seconda condizione non è soddisfatta, poiché esiste un operatore non lineare che opera x (t). Quindi, il sistema non è lineare.

Se vogliamo definire questo sistema, possiamo dire che i sistemi, che non sono lineari, sono sistemi non lineari. Chiaramente, in questo caso dovrebbero essere soddisfatte tutte le condizioni che vengono violate nei sistemi lineari.

Condizioni

• L'output non dovrebbe essere zero quando l'input applicato è zero.

• Qualsiasi operatore non lineare può essere applicato all'ingresso o all'uscita per rendere il sistema non lineare.

Esempi

Per scoprire se i sistemi dati sono lineari o non lineari.

a) $y(t) = e^{x(t)}$

Nel sistema di cui sopra, la prima condizione è soddisfatta perché se rendiamo zero l'ingresso, l'uscita è 1. Inoltre, all'ingresso viene applicato un operatore esponenziale non lineare. Chiaramente, è un caso di sistema non lineare.

b) $y(t) = x(t+1)+x(t-1)$

Il tipo di sistema di cui sopra si occupa di valori passati e futuri. Tuttavia, se rendiamo zero il suo input, non esiste nessuno dei suoi valori. Pertanto, possiamo dire che se l'input è zero, anche la versione di input scalata e spostata nel tempo sarà zero, il che viola la nostra prima condizione. Di nuovo, non è presente alcun operatore non lineare. Pertanto, viene violata anche la seconda condizione. Chiaramente, questo sistema non è un sistema non lineare; piuttosto è un sistema lineare.

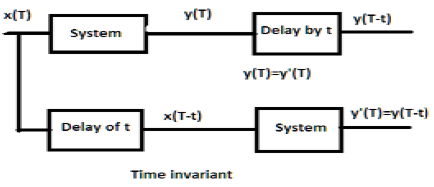
Per un sistema invariante nel tempo, l'uscita e l'input dovrebbero essere ritardati di qualche unità di tempo. Qualsiasi ritardo fornito nell'input deve riflettersi nell'output per un sistema invariante nel tempo.

Esempi

a) $y(T) = x(2T)$

Se l'espressione sopra, viene prima passata attraverso il sistema e poi attraverso il ritardo temporale (come mostrato nella parte superiore della figura); quindi l'uscita diventerà$x(2T-2t)$. Ora, la stessa espressione viene fatta passare prima attraverso un ritardo temporale e poi attraverso il sistema (come mostrato nella parte inferiore della figura). L'output diventerà$x(2T-t)$.

Quindi, il sistema non è un sistema invariante nel tempo.

b) $y(T) = \sin [x(T)]$

Se il segnale viene prima passato attraverso il sistema e poi attraverso il processo di ritardo, l'uscita sarà $\sin x(T-t)$. Allo stesso modo, se il sistema passa prima attraverso il ritardo di tempo e poi attraverso il sistema, l'output sarà$\sin x(T-t)$. Possiamo vedere chiaramente che entrambe le uscite sono le stesse. Quindi, il sistema è invariante nel tempo.

Per un sistema con variante temporale, inoltre, l'uscita e l'ingresso dovrebbero essere ritardati di una certa costante di tempo, ma il ritardo all'ingresso non dovrebbe riflettersi sull'uscita. Tutti i casi di scala temporale sono esempi di sistema di varianti temporali. Allo stesso modo, quando il coefficiente nella relazione di sistema è una funzione del tempo, allora anche il sistema è una variante temporale.

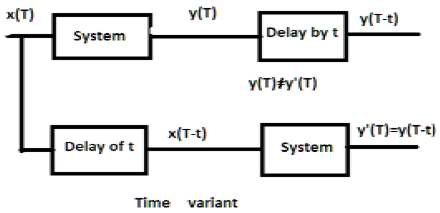
Esempi

a) $y(t) = x[\cos T]$

Se il segnale di cui sopra viene prima fatto passare attraverso il sistema e poi attraverso il ritardo, l'uscita sarà $x\cos (T-t)$. Se è passato prima attraverso il ritardo temporale e poi attraverso il sistema, lo sarà$x(\cos T-t)$. Poiché le uscite non sono le stesse, il sistema è variante temporale.

b) $y(T) = \cos T.x(T)$

Se l'espressione di cui sopra viene prima passata attraverso il sistema e poi attraverso il ritardo, l'output sarà $\cos(T-t)x(T-t)$. Tuttavia, se l'espressione viene passata prima attraverso il ritardo di tempo e poi attraverso il sistema, l'output sarà$\cos T.x(T-t)$. Poiché le uscite non sono le stesse, chiaramente il sistema è una variante temporale.

Un sistema stabile soddisfa la condizione BIBO (ingresso limitato per uscita limitata). Qui, limitato significa finito in ampiezza. Per un sistema stabile, l'output dovrebbe essere limitato o finito, per un input finito o limitato, in ogni istante di tempo.

Alcuni esempi di ingressi limitati sono funzioni di seno, coseno, CC, segno e passo unitario.

Esempi

a) $y(t) = x(t)+10$

Qui, per un input limitato definito, possiamo ottenere output limitato definito, ad esempio se mettiamo $x(t) = 2, y(t) = 12$che è delimitato in natura. Pertanto, il sistema è stabile.

b) $y(t) = \sin [x(t)]$

Nell'espressione data, sappiamo che le funzioni seno hanno un confine definito di valori, che si trova tra -1 e +1. Quindi, qualunque valore sostituiremo in x (t), otterremo i valori all'interno del nostro confine. Pertanto, il sistema è stabile.

I sistemi instabili non soddisfano le condizioni BIBO. Pertanto, per un input limitato, non possiamo aspettarci un output limitato in caso di sistemi instabili.

Esempi

a) $y(t) = tx(t)$

Qui, per un input finito, non possiamo aspettarci un output finito. Ad esempio, se metteremo$x(t) = 2 \Rightarrow y(t) = 2t$. Questo non è un valore finito perché non conosciamo il valore di t. Quindi, può essere variato da qualsiasi luogo. Pertanto, questo sistema non è stabile. È un sistema instabile.

b) $y(t) = \frac{x(t)}{\sin t}$

Abbiamo discusso in precedenza, che la funzione seno ha un intervallo definito da -1 a +1; ma qui è presente nel denominatore. Quindi, nel peggiore dei casi, se mettiamo t = 0 e la funzione seno diventa zero, allora l'intero sistema tenderà all'infinito. Pertanto, questo tipo di sistema non è affatto stabile. Ovviamente, questo è un sistema instabile.

Example 1 - Controlla se $y(t) = x*(t)$ è lineare o non lineare.

Solution- La funzione rappresenta il coniugato di input. Può essere verificato dalla prima legge di omogeneità e legge di additività o dalle due regole. Tuttavia, la verifica attraverso le regole è molto più semplice, quindi lo faremo.

Se l'ingresso al sistema è zero, anche l'uscita tende a zero. Pertanto, la nostra prima condizione è soddisfatta. Non vi è alcun operatore non lineare utilizzato né in ingresso né in uscita. Pertanto, il sistema è lineare.

Example 2 - Controlla se $y(t)=\begin{cases}x(t+1), & t > 0\\x(t-1), & t\leq 0\end{cases}$ è lineare o non lineare

Solution- Chiaramente, possiamo vedere che quando il tempo diventa minore o uguale a zero l'ingresso diventa zero. Quindi, possiamo dire che a zero input anche l'output è zero e la nostra prima condizione è soddisfatta.

Anche in questo caso, non vi è alcun operatore non lineare utilizzato in ingresso né in uscita. Pertanto, il sistema è lineare.

Example 3 - Controlla se $y(t) = \sin t.x(t)$ è stabile o no.

Solution - Supponiamo di aver preso il valore di x (t) come 3. Qui, la funzione seno è stata moltiplicata con essa e il valore massimo e minimo della funzione seno varia tra -1 e +1.

Pertanto, anche il valore massimo e minimo dell'intera funzione varierà tra -3 e +3. Pertanto, il sistema è stabile perché qui stiamo ottenendo un input limitato per un output limitato.

Discrete Time Fourier Transform (DTFT) esiste per i segnali di energia e potenza. La trasformata Z non esiste anche per segnali di tipo energia o potenza (NENP), solo fino a un certo punto. Il rimpiazzo$z=e^{jw}$ viene utilizzato per la conversione da trasformazione Z a DTFT solo per segnali assolutamente sommabili.

Quindi, la trasformata Z del segnale temporale discreto x (n) in una serie di potenze può essere scritta come -

$$X(z) = \sum_{n-\infty}^\infty x(n)Z^{-n}$$

L'equazione sopra rappresenta un'equazione di trasformazione Z bilaterale.

Generalmente, quando un segnale viene trasformato in Z, può essere rappresentato come:

$$X(Z) = Z[x(n)]$$

O $x(n) \longleftrightarrow X(Z)$

Se si tratta di un segnale temporale continuo, le trasformate Z non sono necessarie perché vengono utilizzate le trasformazioni di Laplace. Tuttavia, i segnali di tempo discreto possono essere analizzati solo tramite trasformate Z.

Regione di Convergenza

La regione di convergenza è l'intervallo della variabile complessa Z nel piano Z. La trasformazione Z del segnale è finita o convergente. Quindi, ROC rappresenta quell'insieme di valori di Z, per cui X (Z) ha un valore finito.

Proprietà di ROC

• ROC non include alcun palo.
• Per il segnale del lato destro, ROC sarà fuori dal cerchio nel piano Z.
• Per il segnale sul lato sinistro, ROC sarà all'interno del cerchio nel piano Z.
• Per la stabilità, ROC include il cerchio unitario nel piano Z.
• Per il segnale su entrambi i lati, ROC è un anello nel piano Z.
• Per il segnale di durata finita, ROC è l'intero piano Z.

La trasformata Z è caratterizzata in modo univoco da:

• Espressione di X (Z)
• ROC di X (Z)

Segnali e loro ROC

x (n)	X (Z)	ROC
$\delta(n)$	$1$	Intero piano Z.
$U(n)$	$1/(1-Z^{-1})$	Mod (Z)> 1
$a^nu(n)$	$1/(1-aZ^{-1})$	Mod (Z)> Mod (a)
$-a^nu(-n-1)$	$1/(1-aZ^{-1})$	Mod (Z) <Mod (a)
$na^nu(n)$	$aZ^{-1}/(1-aZ^{-1})^2$	Mod (Z)> Mod (a)
$-a^nu(-n-1)$	$aZ^{-1}/(1-aZ^{-1})^2$	Mod (Z) <Mod (a)
$U(n)\cos \omega n$	$(Z^2-Z\cos \omega)/(Z^2-2Z \cos \omega +1)$	Mod (Z)> 1
$U(n)\sin \omega n$	$(Z\sin \omega)/(Z^2-2Z \cos \omega +1)$	Mod (Z)> 1

Esempio

Cerchiamo di trovare la trasformata Z e il ROC di un segnale dato come $x(n) = \lbrace 7,3,4,9,5\rbrace$, dove l'origine della serie è 3.

Solution - Applicando la formula che abbiamo -

$X(z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-1}^3 x(n)Z^{-n}$

$= x(-1)Z+x(0)+x(1)Z^{-1}+x(2)Z^{-2}+x(3)Z^{-3}$

$= 7Z+3+4Z^{-1}+9Z^{-2}+5Z^{-3}$

ROC è l'intero piano Z escludendo Z = 0, ∞, -∞

In questo capitolo, comprenderemo le proprietà di base delle trasformate Z.

Linearità

Afferma che quando due o più segnali discreti individuali vengono moltiplicati per costanti, anche le rispettive trasformate Z verranno moltiplicate per le stesse costanti.

Matematicamente,

$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$

Proof - Lo sappiamo,

$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$

$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$

$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= a_1X_1(z)+a_2X_2(z)$ (Quindi dimostrato)

Qui, il ROC è $ROC_1\bigcap ROC_2$.

Tempo di spostamento

La proprietà Time shifting descrive come il cambiamento nel dominio del tempo nel segnale discreto influenzerà il dominio Z, che può essere scritto come;

$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$

O $x(n-1)\longleftrightarrow Z^{-1}X(Z)$

Proof -

Permettere $y(P) = X(P-K)$

$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$

$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$

Sia s = pk

$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$

$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$

$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$

$= Z^{-k}X(Z)$ (Quindi dimostrato)

Qui, ROC può essere scritto come Z = 0 (p> 0) o Z = ∞ (p <0)

Esempio

U (n) e U (n-1) possono essere tracciati come segue

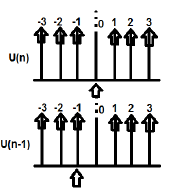
La trasformazione Z di U (n) cabina deve essere scritta come;

$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$

La trasformazione Z di U (n-1) può essere scritta come;

$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$

Ecco $x(n-n_0) = Z^{-n_0}X(Z)$ (Quindi dimostrato)

Scala temporale

La proprietà Time Scaling ci dice quale sarà il dominio Z del segnale quando il tempo viene scalato nella sua forma discreta, che può essere scritta come;

$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$

Proof -

Permettere $y(p) = a^{p}x(p)$

$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$

$= X(a^{-1}Z)$(Quindi dimostrato)

ROC: = Mod (ar1) <Mod (Z) <Mod (ar2) dove Mod = Modulo

Esempio

Determiniamo la trasformazione Z di $x(n) = a^n \cos \omega n$ utilizzando la proprietà Time scaling.

Solution -

Sappiamo già che la trasformazione Z del segnale $\cos (\omega n)$ è dato da -

$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$

Ora, applicando la proprietà Time scaling, la trasformazione Z di $a^n \cos \omega n$ può essere scritto come;

$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$

$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$

$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$

Differenziazione successiva

La proprietà Successive Differentiation mostra che la trasformata Z avrà luogo quando differenziamo il segnale discreto nel dominio del tempo, rispetto al tempo. Questo è mostrato come sotto.

$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$

Proof -

Considera l'LHS dell'equazione: $\frac{dx(n)}{dn}$

$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$

$= x(n)-X(n-1)$

$= x(Z)-Z^{-1}x(Z)$

$= (1-Z^{-1})x(Z)$ (Quindi dimostrato)

ROC: R1 <Mod (Z) <R2

Esempio

Cerchiamo di trovare la trasformata Z di un segnale dato da $x(n) = n^2u(n)$

Per proprietà possiamo scrivere

$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$

$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$

$= Z/((Z-1)^2$

$= y(let)$

Ora, Z [ny] può essere scoperto applicando nuovamente la proprietà,

$Z(n,y) = -Z\frac{dy}{dz}$

$= -Z\frac{d[Z/(Z-1)^3]}{dz}$

$= Z(Z+1)/(Z-1)^2$

Convoluzione

Questo rappresenta il cambiamento nel dominio Z del sistema quando si verifica una convoluzione nella forma del segnale discreto, che può essere scritta come:

$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$

Proof -

$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$

Sia nk = l, quindi l'equazione precedente cab sia scritta come -

$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$

$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$

$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$

$= X_1(Z).X_2(Z)$ (Quindi dimostrato)

ROC:$ROC\bigcap ROC2$

Esempio

Troviamo la convoluzione data da due segnali

$x_1(n) = \lbrace 3,-2,2\rbrace$ ... (eq.1)

$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ... (eq. 2)

La trasformazione Z della prima equazione può essere scritta come;

$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$

$= 3-2Z^{-1}+2Z^{-2}$

La trasformazione Z del secondo segnale può essere scritta come;

$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

Quindi, la convoluzione dei due segnali precedenti è data da:

$X(Z) = [x_1(Z)^*x_2(Z)]$

$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$

Prendendo la trasformazione Z inversa che otteniamo,

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$

Teorema del valore iniziale

Se x (n) è una successione causale, che ha la sua trasformazione Z come X (z), allora il teorema del valore iniziale può essere scritto come;

$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$

Proof - Lo sappiamo,

$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$

Espandendo la serie di cui sopra, otteniamo;

$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

Nel caso precedente se Z → ∞ allora $Z^{-n}\rightarrow 0$ (Perché n> 0)

Pertanto, possiamo dire;

$\lim_{z \to \infty}X(z) = X(0)$ (Quindi dimostrato)

Teorema del valore finale

Il Teorema del valore finale afferma che se la trasformata Z di un segnale è rappresentata come X (Z) ei poli sono tutti all'interno del cerchio, il suo valore finale è indicato come x (n) o X (∞) e può essere scritto come -

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$

Conditions -

• È applicabile solo per i sistemi causali.
• $X(Z)(1-Z^{-1})$ dovrebbe avere poli all'interno del cerchio unitario nel piano Z.

Proof - Lo sappiamo

$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$

Qui possiamo applicare la proprietà avanzata della trasformazione Z unilaterale. Quindi, l'equazione sopra può essere riscritta come;

$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$

Ora mettendo z = 1 nell'equazione sopra, possiamo espandere l'equazione sopra -

$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$

Questo può essere formulato come;

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(Quindi dimostrato)

Esempio

Troviamo il valore Iniziale e Finale di x (n) il cui segnale è dato da

$X(Z) = 2+3Z^{-1}+4Z^{-2}$

Solution - Per prima cosa, troviamo il valore iniziale del segnale applicando il teorema

$x(0) = \lim_{z \to \infty}X(Z)$

$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$

$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$

Cerchiamo ora di trovare il valore finale del segnale applicando il teorema

$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$

$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$

$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$

$= 2+1+1-4 = 0$

Some other properties of Z-transform are listed below -

Differenziazione in frequenza

Fornisce la variazione nel dominio Z del segnale, quando il suo segnale discreto è differenziato rispetto al tempo.

$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$

Il suo ROC può essere scritto come;

$r_2< Mod(Z)< r_1$

Esempio

Troviamo il valore di x (n) tramite Differenziazione in frequenza, il cui segnale discreto nel dominio Z è dato da $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$

Per proprietà, possiamo scriverlo

$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$

$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$

$= (aZ^{-1})/(1+aZ^{-1})$

$= 1-1/(1+aZ^{-1})$

$nx(n) = \delta(n)-(-a)^nu(n)$

$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$

Moltiplicazione nel tempo

Fornisce la variazione nel dominio Z del segnale quando la moltiplicazione avviene a livello di segnale discreto.

$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$

Coniugazione nel tempo

Questo raffigura la rappresentazione del segnale discreto coniugato nel dominio Z.

$X^*(n)\longleftrightarrow X^*(Z^*)$

Un sistema, che ha una funzione di sistema, può essere stabile solo se tutti i poli si trovano all'interno del cerchio unitario. In primo luogo, controlliamo se il sistema è causale o meno. Se il sistema è causale, allora andiamo per la sua determinazione della stabilità BIBO; dove la stabilità BIBO si riferisce all'ingresso limitato per la condizione di uscita limitata.

Questo può essere scritto come;

$Mod(X(Z))< \infty$

$= Mod(\sum x(n)Z^{-n})< \infty$

$= \sum Mod(x(n)Z^{-n})< \infty$

$= \sum Mod[x(n)(re^{jw})^{-n}]< 0$

$= \sum Mod[x(n)r^{-n}]Mod[e^{-jwn}]< \infty$

$= \sum_{n = -\infty}^\infty Mod[x(n)r^{-n}]< \infty$

L'equazione precedente mostra la condizione per l'esistenza della trasformata Z.

Tuttavia, la condizione per l'esistenza del segnale DTFT è

$$\sum_{n = -\infty}^\infty Mod(x(n)< \infty$$

Esempio 1

Proviamo a scoprire la trasformata Z del segnale, che è data come

$x(n) = -(-0.5)^{-n}u(-n)+3^nu(n)$

$= -(-2)^nu(n)+3^nu(n)$

Solution - Qui, per $-(-2)^nu(n)$ il ROC è Left sided e Z <2

Per $3^nu(n)$ ROC è lato destro e Z> 3

Quindi, qui la trasformata Z del segnale non esisterà perché non esiste una regione comune.

Esempio 2

Cerchiamo di scoprire la trasformata Z del segnale dato da

$x(n) = -2^nu(-n-1)+(0.5)^nu(n)$

Solution - Qui, per $-2^nu(-n-1)$ Il ROC del segnale è Left sided e Z <2

Per segnale $(0.5)^nu(n)$ ROC è lato destro e Z> 0,5

Quindi, il ROC comune formato come 0,5 <Z <2

Pertanto, la trasformazione Z può essere scritta come;

$X(Z) = \lbrace\frac{1}{1-2Z^{-1}}\rbrace+\lbrace\frac{1}{(1-0.5Z)^{-1}}\rbrace$

Esempio 3

Proviamo a scoprire la trasformata Z del segnale, che è data come $x(n) = 2^{r(n)}$

Solution- r (n) è il segnale di rampa. Quindi il segnale può essere scritto come;

$x(n) = 2^{nu(n)}\lbrace 1, n<0 (u(n)=0)\quad and\quad2^n, n\geq 0(u(n) = 1)\rbrace$

$= u(-n-1)+2^nu(n)$

Ecco, per il segnale $u(-n-1)$ e ROC Z <1 e per $2^nu(n)$ con ROC è Z> 2.

Quindi, la trasformazione Z del segnale non esisterà.

Z-Trasforma per il sistema causale

Il sistema causale può essere definito come $h(n) = 0,n<0$. Per il sistema causale, ROC sarà al di fuori del cerchio nel piano Z.

$H(Z) = \displaystyle\sum\limits_{n = 0}^{\infty}h(n)Z^{-n}$

Espandendo l'equazione di cui sopra,

$H(Z) = h(0)+h(1)Z^{-1}+h(2)Z^{-2}+...\quad...\quad...$

$= N(Z)/D(Z)$

Per i sistemi causali, l'espansione della funzione di trasferimento non include i poteri positivi di Z. Per il sistema causale, l'ordine del numeratore non può superare l'ordine del denominatore. Questo può essere scritto come-

$\lim_{z \rightarrow \infty}H(Z) = h(0) = 0\quad or\quad Finite$

Per la stabilità del sistema causale, i poli della funzione di trasferimento dovrebbero essere all'interno del cerchio unitario nel piano Z.

Trasformata Z per il sistema anti-causale

Il sistema anti-causale può essere definito come $h(n) = 0, n\geq 0$. Per il sistema anti-causale, i poli della funzione di trasferimento dovrebbero trovarsi al di fuori del cerchio unitario nel piano Z. Per il sistema anti-causale, ROC sarà all'interno del cerchio nel piano Z.

Se vogliamo analizzare un sistema, che è già rappresentato nel dominio della frequenza, come segnale temporale discreto, allora andiamo per la trasformazione Z inversa.

Matematicamente, può essere rappresentato come;

$$x(n) = Z^{-1}X(Z)$$

dove x (n) è il segnale nel dominio del tempo e X (Z) è il segnale nel dominio della frequenza.

Se vogliamo rappresentare l'equazione di cui sopra in formato integrale, possiamo scriverla come

$$x(n) = (\frac{1}{2\Pi j})\oint X(Z)Z^{-1}dz$$

Qui, l'integrale è su un percorso chiuso C. Questo percorso è all'interno del ROC della x (z) e contiene l'origine.

Metodi per trovare la trasformazione Z inversa

Quando l'analisi è necessaria in formato discreto, convertiamo nuovamente il segnale nel dominio della frequenza in formato discreto tramite trasformazione Z inversa. Seguiamo i seguenti quattro modi per determinare la trasformazione Z inversa.

• Metodo di divisione lunga
• Metodo di espansione della frazione parziale
• Metodo del residuo o del contorno integrale

Metodo di divisione lunga

In questo metodo, la trasformata Z del segnale x (z) può essere rappresentata come il rapporto del polinomio come mostrato di seguito;

$$x(z)=N(Z)/D(Z)$$

Ora, se continuiamo a dividere il numeratore per denominatore, otterremo una serie come mostrato di seguito

$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...\quad...\quad...$$

La sequenza di cui sopra rappresenta la serie di trasformata Z inversa del segnale dato (per n≥0) e il sistema di cui sopra è causale.

Tuttavia per n <0 la serie può essere scritta come;

$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...\quad...\quad...$$

Metodo di espansione della frazione parziale

Anche qui il segnale viene espresso prima nella forma N (z) / D (z).

Se è una frazione razionale sarà rappresentata come segue;

$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...\quad...\quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...\quad...\quad...+a_nZ^{-N})$

Quello sopra è improprio quando m <ne un ≠ 0

Se il rapporto non è corretto (cioè improprio), dobbiamo convertirlo nella forma corretta per risolverlo.

Metodo del residuo o del contorno integrale

In questo metodo, otteniamo la trasformata Z inversa x (n) sommando i residui di $[x(z)Z^{n-1}]$a tutti i poli. Matematicamente, questo può essere espresso come

$$x(n) = \displaystyle\sum\limits_{all\quad poles\quad X(z)}residues\quad of[x(z)Z^{n-1}]$$

Qui, il residuo per qualsiasi polo di ordine m $z = \beta$ è

$$Residues = \frac{1}{(m-1)!}\lim_{Z \rightarrow \beta}\lbrace \frac{d^{m-1}}{dZ^{m-1}}\lbrace (z-\beta)^mX(z)Z^{n-1}\rbrace$$

Esempio 1

Trova la risposta del sistema $s(n+2)-3s(n+1)+2s(n) = \delta (n)$, quando tutte le condizioni iniziali sono zero.

Solution - Prendendo la trasformazione Z su entrambi i lati dell'equazione precedente, otteniamo

$$S(z)Z^2-3S(z)Z^1+2S(z) = 1$$

$\Rightarrow S(z)\lbrace Z^2-3Z+2\rbrace = 1$

$\Rightarrow S(z) = \frac{1}{\lbrace z^2-3z+2\rbrace}=\frac{1}{(z-2)(z-1)} = \frac{\alpha _1}{z-2}+\frac{\alpha _2}{z-1}$

$\Rightarrow S(z) = \frac{1}{z-2}-\frac{1}{z-1}$

Prendendo la trasformata Z inversa dell'equazione precedente, otteniamo

$S(n) = Z^{-1}[\frac{1}{Z-2}]-Z^{-1}[\frac{1}{Z-1}]$

$= 2^{n-1}-1^{n-1} = -1+2^{n-1}$

Esempio 2

Trova la funzione di sistema H (z) e la risposta campionaria h (n) del sistema la cui equazione alle differenze è descritta come sotto

$y(n) = \frac{1}{2}y(n-1)+2x(n)$

dove, y (n) e x (n) sono rispettivamente l'uscita e l'input del sistema.

Solution - Prendendo la trasformata Z dell'equazione alle differenze sopra, otteniamo

$y(z) = \frac{1}{2}Z^{-1}Y(Z)+2X(z)$

$= Y(Z)[1-\frac{1}{2}Z^{-1}] = 2X(Z)$

$= H(Z) = \frac{Y(Z)}{X(Z)} = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$

Questo sistema ha un polo a $Z = \frac{1}{2}$ e $Z = 0$ e $H(Z) = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$

Quindi, prendendo la trasformata Z inversa di quanto sopra, otteniamo

$h(n) = 2(\frac{1}{2})^nU(n)$

Esempio 3

Determina Y (z), n≥0 nel caso seguente:

$y(n)+\frac{1}{2}y(n-1)-\frac{1}{4}y(n-2) = 0\quad given\quad y(-1) = y(-2) = 1$

Solution - Applicando la trasformata Z all'equazione precedente, otteniamo

$Y(Z)+\frac{1}{2}[Z^{-1}Y(Z)+Y(-1)]-\frac{1}{4}[Z^{-2}Y(Z)+Z^{-1}Y(-1)+4(-2)] = 0$

$\Rightarrow Y(Z)+\frac{1}{2Z}Y(Z)+\frac{1}{2}-\frac{1}{4Z^2}Y(Z)-\frac{1}{4Z}-\frac{1}{4} = 0$

$\Rightarrow Y(Z)[1+\frac{1}{2Z}-\frac{1}{4Z^2}] =\frac{1}{4Z}-\frac{1}{2}$

$\Rightarrow Y(Z)[\frac{4Z^2+2Z-1}{4Z^2}] = \frac{1-2Z}{4Z}$

$\Rightarrow Y(Z) = \frac{Z(1-2Z)}{4Z^2+2Z-1}$

Come la trasformata di Fourier del segnale temporale continuo, la trasformata di Fourier a tempo discreto può essere utilizzata per rappresentare una sequenza discreta nella sua rappresentazione nel dominio della frequenza equivalente e nel sistema temporale discreto LTI e per sviluppare vari algoritmi di calcolo.

X (jω) in FT continua, è una funzione continua di x (n). Tuttavia, DFT si occupa di rappresentare x (n) con campioni del suo spettro X (ω). Quindi, questo strumento matematico ha molta importanza dal punto di vista computazionale nella rappresentazione conveniente. Tramite questo strumento è possibile elaborare sia sequenze periodiche che non periodiche. Le sequenze periodiche devono essere campionate estendendo il periodo all'infinito.

Campionamento nel dominio della frequenza

Dall'introduzione, è chiaro che abbiamo bisogno di sapere come procedere attraverso il campionamento nel dominio della frequenza, cioè il campionamento X (ω). Quindi, la relazione tra trasformata di Fourier campionata e DFT viene stabilita nel modo seguente.

Allo stesso modo, le sequenze periodiche possono adattarsi a questo strumento estendendo il periodo N all'infinito.

Sia una sequenza Non periodica, $X(n) = \lim_{N \to \infty}x_N(n)$

Definendo la sua trasformata di Fourier,

$X(\omega ) = \sum_{n=-\infty}^\infty x(n)e^{-jwn}X(K\delta \omega)$

Qui, X (ω) viene campionato periodicamente, ad ogni δω intervallo di radianti.

Poiché X (ω) è periodico in 2π radianti, richiediamo campioni solo nell'intervallo fondamentale. I campioni vengono prelevati dopo intervalli equidistanti nella gamma di frequenza 0≤ω≤2π. La spaziatura tra gli intervalli equivalenti è$\delta \omega = \frac{2\pi }{N}k$ radiante.

Ora valutando, $\omega = \frac{2\pi}{N}k$

$X(\frac{2\pi}{N}k) = \sum_{n = -\infty}^\infty x(n)e^{-j2\pi nk/N},$ ... eq (2)

dove k = 0,1, …… N-1

Dopo aver suddiviso quanto sopra e scambiato l'ordine di sommatoria

$X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}[\displaystyle\sum\limits_{l = -\infty}^\infty x(n-Nl)]e^{-j2\pi nk/N}$ ... eq (3)

$\sum_{l=-\infty}^\infty x(n-Nl) = x_p(n) = a\quad periodic\quad function\quad of\quad period\quad N\quad and\quad its\quad fourier\quad series\quad = \sum_{k = 0}^{N-1}C_ke^{j2\pi nk/N}$

dove, n = 0,1,… .., N-1; 'p' sta per entità o funzione periodica

I coefficienti di Fourier sono,

$C_k = \frac{1}{N}\sum_{n = 0}^{N-1}x_p(n)e^{-j2\pi nk/N}$k = 0,1,…, N-1 ... eq (4)

Confrontando le equazioni 3 e 4, otteniamo;

$NC_k = X(\frac{2\pi}{N}k)$k = 0,1,…, N-1 ... eq (5)

$NC_k = X(\frac{2\pi}{N}k) = X(e^{jw}) = \displaystyle\sum\limits_{n = -\infty}^\infty x_p(n)e^{-j2\pi nk/N}$... eq (6)

Dall'espansione della serie di Fourier,

$x_p(n) = \frac{1}{N}\displaystyle\sum\limits_{k = 0}^{N-1}NC_ke^{j2\pi nk/N} = \frac{1}{N}\sum_{k = 0}^{N-1}X(\frac{2\pi}{N}k)e^{j2\pi nk/N}$... eq (7)

Dove n = 0,1,…, N-1

Qui, abbiamo ottenuto il segnale periodico da X (ω). $x(n)$ può essere estratto da $x_p(n)$ solo se non sono presenti alias nel dominio del tempo. $N\geq L$

N = periodo di $x_p(n)$ L = periodo di $x(n)$

$x(n) = \begin{cases}x_p(n), & 0\leq n\leq N-1\\0, & Otherwise\end{cases}$

La mappatura si ottiene in questo modo.

Proprietà di DFT

Linearità

Afferma che la DFT di una combinazione di segnali è uguale alla somma della DFT dei singoli segnali. Prendiamo due segnali x ₁ (n) e x ₂ (n), i cui DFT sono rispettivamente X ₁ (ω) e X ₂ (ω). Quindi se

$x_1(n)\rightarrow X_1(\omega)$e$x_2(n)\rightarrow X_2(\omega)$

Poi $ax_1(n)+bx_2(n)\rightarrow aX_1(\omega)+bX_2(\omega)$

dove a e b sono costanti.

Symmetry

The symmetry properties of DFT can be derived in a similar way as we derived DTFT symmetry properties. We know that DFT of sequence x(n) is denoted by X(K). Now, if x(n) and X(K) are complex valued sequence, then it can be represented as under

$x(n) = x_R(n)+jx_1(n),0\leq n\leq N-1$

And $X(K) = X_R(K)+jX_1(K),0\leq K\leq N-1$

Duality Property

Let us consider a signal x(n), whose DFT is given as X(K). Let the finite duration sequence be X(N). Then according to duality theorem,

If, $x(n)\longleftrightarrow X(K)$

Then, $X(N)\longleftrightarrow Nx[((-k))_N]$

So, by using this theorem if we know DFT, we can easily find the finite duration sequence.

Complex Conjugate Properties

Suppose, there is a signal x(n), whose DFT is also known to us as X(K). Now, if the complex conjugate of the signal is given as x*(n), then we can easily find the DFT without doing much calculation by using the theorem shown below.

If, $x(n)\longleftrightarrow X(K)$

Then, $x*(n)\longleftrightarrow X*((K))_N = X*(N-K)$

Circular Frequency Shift

The multiplication of the sequence x(n) with the complex exponential sequence $e^{j2\Pi kn/N}$ is equivalent to the circular shift of the DFT by L units in frequency. This is the dual to the circular time shifting property.

If, $x(n)\longleftrightarrow X(K)$

Then, $x(n)e^{j2\Pi Kn/N}\longleftrightarrow X((K-L))_N$

Multiplication of Two Sequence

If there are two signal x₁(n) and x₂(n) and their respective DFTs are X₁(k) and X₂(K), then multiplication of signals in time sequence corresponds to circular convolution of their DFTs.

If, $x_1(n)\longleftrightarrow X_1(K)\quad\&\quad x_2(n)\longleftrightarrow X_2(K)$

Then, $x_1(n)\times x_2(n)\longleftrightarrow X_1(K)© X_2(K)$

Parseval’s Theorem

For complex valued sequences x(n) and y(n), in general

If, $x(n)\longleftrightarrow X(K)\quad \&\quad y(n)\longleftrightarrow Y(K)$

Then, $\sum_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\sum_{k = 0}^{N-1}X(K)Y^*(K)$

We know that when $\omega = 2\pi K/N$ and $N\rightarrow \infty,\omega$ becomes a continuous variable and limits summation become $-\infty$ to $+\infty$.

Therefore,

$$NC_k = X(\frac{2\pi}{N}k) = X(e^{j\omega}) = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{\frac{-j2\pi nk}{N}} = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{-j\omega n}$$

Discrete Time Fourier Transform (DTFT)

We know that, $X(e^{j\omega}) = \sum_{n = -\infty}^\infty x(n)e^{-j\omega n}$

Where, $X(e^{j\omega})$ is continuous and periodic in ω and with period 2π.…eq(1)

Now,

$x_p(n) = \sum_{k = 0}^{N-1}NC_ke^{j2 \pi nk/N}$ … From Fourier series

$x_p(n) = \frac{1}{2\pi}\sum_{k=0}^{N-1}NC_ke^{j2\pi nk/N}\times \frac{2\pi}{N}$

ω becomes continuous and $\frac{2\pi}{N}\rightarrow d\omega$, because of the reasons cited above.

$x(n) = \frac{1}{2\pi}\int_{n = 0}^{2\pi}X(e^{j\omega})e^{j\omega n}d\omega$…eq(2)

Inverse Discrete Time Fourier Transform

Symbolically,

$x(n)\Longleftrightarrow x(e^{j\omega})$(The Fourier Transform pair)

Necessary and sufficient condition for existence of Discrete Time Fourier Transform for a non-periodic sequence x(n) is absolute summable.

i.e.$\sum_{n = -\infty}^\infty|x(n)|<\infty$

Properties of DTFT

• Linearity : $a_1x_1(n)+a_2x_2(n)\Leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$

• Time shifting − $x(n-k)\Leftrightarrow e^{-j\omega k}.X(e^{j\omega})$

• Time Reversal − $x(-n)\Leftrightarrow X(e^{-j\omega})$

• Frequency shifting − $e^{j\omega _0n}x(n)\Leftrightarrow X(e^{j(\omega -\omega _0)})$

• Differentiation frequency domain − $nx(n) = j\frac{d}{d\omega}X(e^{j\omega})$

• Convolution − $x_1(n)*x_2(n)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$

• Multiplication − $x_1(n)\times x_2(n)\Leftrightarrow X_1(e^{j\omega})*X_2(e^{j\omega})$

• Co-relation − $y_{x_1\times x_2}(l)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$

• Modulation theorem − $x(n)\cos \omega _0n = \frac{1}{2}[X_1(e^{j(\omega +\omega _0})*X_2(e^{jw})$

• Symmetry −$x^*(n)\Leftrightarrow X^*(e^{-j\omega})$ ;

  $x^*(-n)\Leftrightarrow X^*(e^{j\omega})$ ;

  $Real[x(n)]\Leftrightarrow X_{even}(e^{j\omega})$ ;

  $Imag[x(n)]\Leftrightarrow X_{odd}(e^{j\omega})$ ;

  $x_{even}(n)\Leftrightarrow Real[x(e^{j\omega})]$ ;

  $x_{odd}(n)\Leftrightarrow Imag[x(e^{j\omega})]$ ;

• Parseval’s theorem − $\sum_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$

Earlier, we studied sampling in frequency domain. With that basic knowledge, we sample $X(e^{j\omega})$ in frequency domain, so that a convenient digital analysis can be done from that sampled data. Hence, DFT is sampled in both time and frequency domain. With the assumption $x(n) = x_p(n)$

Hence, DFT is given by −

$X(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{-\frac{j2\pi nk}{N}}$,k=0,1,….,N−1…eq(3)

And IDFT is given by −

$X(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k)e^{\frac{j2\pi nk}{N}}$,n=0,1,….,N−1…eq(4)

$\therefore x(n)\Leftrightarrow X(k)$

Twiddle Factor

It is denoted as $W_N$ and defined as $W_N = e^{-j2\pi /N}$ . Its magnitude is always maintained at unity. Phase of $W_N = -2\pi /N$ . It is a vector on unit circle and is used for computational convenience. Mathematically, it can be shown as −

$W_N^r = W_N^{r\pm N} = W_N^{r\pm 2N} = ...$

• It is function of r and period N.

  Consider N = 8, r = 0,1,2,3,….14,15,16,….

  $\Longleftrightarrow W_8^0 = W_8^8 = W_8^{16} = ... = ... = W_8^{32} = ... =1= 1\angle 0$

• $W_8^1 = W_8^9 = W_8^{17} = ... = ... = W_8^{33} = ... =\frac{1}{\sqrt 2}= j\frac{1}{\sqrt 2} = 1\angle-\frac{\pi}{4}$

Linear Transformation

Let us understand Linear Transformation −

We know that,

$DFT(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \sum_{n = 0}^{N-1}x(n).W_n^{-nk};\quad k = 0,1,….,N−1$

$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k).W_N^{-nk};\quad n = 0,1,….,N−1$

Note − Computation of DFT can be performed with N² complex multiplication and N(N-1) complex addition.

$x_N = \begin{bmatrix}x(0)\\x(1)\\.\\.\\x(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad x_N$

$X_N = \begin{bmatrix}X(0)\\X(1)\\.\\.\\X(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad X_N$

$\begin{bmatrix}1 & 1 & 1 & ... & ... & 1\\1 & W_N & W_N^2 & ... & ... & W_N^{N-1}\\. & W_N^2 & W_N^4 & ... & ... & W_N^{2(N-1)}\\.\\1 & W_N^{N-1} & W_N^{2(N-1)} & ... & ... & W_N^{(N-1)(N-1)} \end{bmatrix}$

N - point DFT in matrix term is given by - $X_N = W_Nx_N$

$W_N\longmapsto$ Matrix of linear transformation

$Now,\quad x_N = W_N^{-1}X_N$

IDFT in Matrix form is given by

$$x_N = \frac{1}{N}W_N^*X_N$$

Comparing both the expressions of $x_N,\quad W_N^{-1} = \frac{1}{N}W_N^*$ and $W_N\times W_N^* = N[I]_{N\times N}$

Therefore, $W_N$ is a linear transformation matrix, an orthogonal (unitary) matrix.

From periodic property of $W_N$ and from its symmetric property, it can be concluded that, $W_N^{k+N/2} = -W_N^k$

Circular Symmetry

N-point DFT of a finite duration x(n) of length N≤L, is equivalent to the N-point DFT of periodic extension of x(n), i.e. $x_p(n)$ of period N. and $x_p(n) = \sum_{l = -\infty}^\infty x(n-Nl)$ . Now, if we shift the sequence, which is a periodic sequence by k units to the right, another periodic sequence is obtained. This is known as Circular shift and this is given by,

$$x_p^\prime (n) = x_p(n-k) = \sum_{l = -\infty}^\infty x(n-k-Nl)$$

The new finite sequence can be represented as

$$x_p^\prime (n) = \begin{cases}x_p^\prime(n), & 0\leq n\leq N-1\\0 & Otherwise\end{cases}$$

Example − Let x(n)= {1,2,4,3}, N = 4,

$x_p^\prime (n) = x(n-k,modulo\quad N)\equiv x((n-k))_N\quad;ex-if\quad k=2i.e\quad 2\quad unit\quad right\quad shift\quad and\quad N = 4,$

Assumed clockwise direction as positive direction.

We got, $x\prime(n) = x((n-2))_4$

$x\prime(0) = x((-2))_4 = x(2) = 4$

$x\prime(1) = x((-1))_4 = x(3) = 3$

$x\prime(2) = x((-2))_4 = x(0) = 1$

$x\prime(3) = x((1))_4 = x(1) = 2$

Conclusion − Circular shift of N-point sequence is equivalent to a linear shift of its periodic extension and vice versa.

Circularly even sequence − $x(N-n) = x(n),\quad 1\leq n\leq N-1$

$i.e.x_p(n) = x_p(-n) = x_p(N-n)$

Conjugate even −$x_p(n) = x_p^*(N-n)$

Circularly odd sequence − $x(N-n) = -x(n),\quad 1\leq n\leq N-1$

$i.e.x_p(n) = -x_p(-n) = -x_p(N-n)$

Conjugate odd − $x_p(n) = -x_p^*(N-n)$

Now, $x_p(n) = x_{pe}+x_{po}(n)$, where,

$x_{pe}(n) = \frac{1}{2}[x_p(n)+x_p^*(N-n)]$

$x_{po}(n) = \frac{1}{2}[x_p(n)-x_p^*(N-n)]$

For any real signal x(n),$X(k) = X^*(N-k)$

$X_R(k) = X_R(N-k)$

$X_l(k) = -X_l(N-k)$

$\angle X(k) = -\angle X(N-K)$

Time reversal − reversing sample about the 0^th sample. This is given as;

$x((-n))_N = x(N-n),\quad 0\leq n\leq N-1$

Time reversal is plotting samples of sequence, in clockwise direction i.e. assumed negative direction.

Some Other Important Properties

Other important IDFT properties $x(n)\longleftrightarrow X(k)$

• Time reversal − $x((-n))_N = x(N-n)\longleftrightarrow X((-k))_N = X(N-k)$

• Circular time shift − $x((n-l))_N \longleftrightarrow X(k)e^{j2\pi lk/N}$

• Circular frequency shift − $x(n)e^{j2\pi ln/N} \longleftrightarrow X((k-l))_N$

• Complex conjugate properties −

  $x^*(n)\longleftrightarrow X^*((-k))_N = X^*(N-k)\quad and$

  $x^*((-n))_N = x^*(N-n)\longleftrightarrow X^*(-k)$

• Multiplication of two sequence −

  $x_1(n)\longleftrightarrow X_1(k)\quad and\quad x_2(n)\longleftrightarrow X_2(k)$

  $\therefore x_1(n)x_2(n)\longleftrightarrow X_1(k)\quadⓃ X_2(k)$

• Circular convolution − and multiplication of two DFT

  $x_1(k)\quad Ⓝ x_2(k) =\sum_{k = 0}^{N-1}x_1(n).x_2((m-n))_n,\quad m = 0,1,2,... .,N-1 $

  $x_1(k)\quad Ⓝ x_2(k)\longleftrightarrow X_1(k).X_2(k)$

• Circular correlation − If $x(n)\longleftrightarrow X(k)$ and $y(n)\longleftrightarrow Y(k)$ , then there exists a cross correlation sequence denoted as $\bar Y_{xy}$ such that $\bar Y_{xy}(l) = \sum_{n = 0}^{N-1}x(n)y^*((n-l))_N = X(k).Y^*(k)$

• Parseval’s Theorem − If $x(n)\longleftrightarrow X(k)$ and $y(n)\longleftrightarrow Y(k)$;

  $\displaystyle\sum\limits_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\displaystyle\sum\limits_{n =0}^{N-1}X(k).Y^*(k)$

Let us take two finite duration sequences x₁(n) and x₂(n), having integer length as N. Their DFTs are X₁(K) and X₂(K) respectively, which is shown below −

$$X_1(K) = \sum_{n = 0}^{N-1}x_1(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$ $$X_2(K) = \sum_{n = 0}^{N-1}x_2(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$

Now, we will try to find the DFT of another sequence x₃(n), which is given as X₃(K)

$X_3(K) = X_1(K)\times X_2(K)$

By taking the IDFT of the above we get

$x_3(n) = \frac{1}{N}\displaystyle\sum\limits_{n = 0}^{N-1}X_3(K)e^{\frac{j2\Pi kn}{N}}$

After solving the above equation, finally, we get

$x_3(n) = \displaystyle\sum\limits_{m = 0}^{N-1}x_1(m)x_2[((n-m))_N]\quad m = 0,1,2...N-1$

Comparison points	Linear Convolution	Circular Convolution
Shifting	Linear shifting	Circular shifting
Samples in the convolution result	$N_1+N_2−1$	$Max(N_1,N_2)$
Finding response of a filter	Possible	Possible with zero padding

Methods of Circular Convolution

Generally, there are two methods, which are adopted to perform circular convolution and they are −

• Concentric circle method,
• Matrix multiplication method.

Concentric Circle Method

Let $x_1(n)$ and $x_2(n)$ be two given sequences. The steps followed for circular convolution of $x_1(n)$ and $x_2(n)$ are

• Take two concentric circles. Plot N samples of $x_1(n)$ on the circumference of the outer circle (maintaining equal distance successive points) in anti-clockwise direction.

• For plotting $x_2(n)$, plot N samples of $x_2(n)$ in clockwise direction on the inner circle, starting sample placed at the same point as 0^th sample of $x_1(n)$

• Multiply corresponding samples on the two circles and add them to get output.

• Rotate the inner circle anti-clockwise with one sample at a time.

Matrix Multiplication Method

Matrix method represents the two given sequence $x_1(n)$ and $x_2(n)$ in matrix form.

• One of the given sequences is repeated via circular shift of one sample at a time to form a N X N matrix.

• The other sequence is represented as column matrix.

• The multiplication of two matrices give the result of circular convolution.

DFT provides an alternative approach to time domain convolution. It can be used to perform linear filtering in frequency domain.

Thus,$Y(\omega) = X(\omega).H(\omega)\longleftrightarrow y(n)$.

The problem in this frequency domain approach is that $Y(\omega)$, $X(\omega)$ and $H(\omega)$ are continuous function of ω, which is not fruitful for digital computation on computers. However, DFT provides sampled version of these waveforms to solve the purpose.

Il vantaggio è che, avendo conoscenza di tecniche DFT più veloci come FFT, un algoritmo computazionalmente più efficiente può essere sviluppato per il calcolo digitale del computer rispetto all'approccio nel dominio del tempo.

Considera una sequenza di durata finita, $[x(n) = 0,\quad for,n<0\quad and\quad n\geq L]$ (equazione generalizzata), eccita un filtro lineare con risposta all'impulso $[h(n) = 0,\quad forn<0\quad and\quad n\geq M]$.

$$x(n)y(n)$$ $$output = y(n) = \sum_{k = 0}^{M-1}h(k).x(n-k)$$

Dall'analisi di convoluzione, è chiaro che la durata di y (n) è L + M − 1.

Nel dominio della frequenza,

$$Y(\omega) = X(\omega).H(\omega)$$

Adesso, $Y(\omega)$ è una funzione continua di ω ed è campionata ad un insieme di frequenze discrete con numero di campioni distinti che deve essere uguale o superiore $L+M-1$.

$$DFT\quad size = N\geq L+M-1$$

Con $\omega = \frac{2\pi}{N}k$,

$Y(\omega) = X(k).H(k)$, dove k = 0,1,…., N-1

Dove, X (k) e H (k) sono DFT a N punti di x (n) e h (n) rispettivamente. $x(n)\& h(n)$ sono riempiti con zeri fino alla lunghezza N. Non distorce gli spettri continui $X(\omega)$ e $H(\omega)$. Da$N\geq L+M-1$, N punti DFT della sequenza di output y (n) è sufficiente per rappresentare y (n) nel dominio della frequenza e questi fatti inferiscono che la moltiplicazione di N punti DFT di X (k) e H (k), seguita dal calcolo di N punti IDFT deve fornire y (n).

Ciò implica, convoluzione circolare in N punti di x (n) e H (n) con riempimento zero, uguale alla convoluzione lineare di x (n) e h (n).

Pertanto, DFT può essere utilizzato per il filtraggio lineare.

Caution - N dovrebbe sempre essere maggiore o uguale a $L+M-1$. Altrimenti, l'effetto di aliasing danneggerebbe la sequenza di output.

Supponiamo che la sequenza di input x (n) di lunga durata debba essere elaborata con un sistema avente una risposta all'impulso di durata finita convolgendo le due sequenze. Poiché il filtraggio lineare eseguito tramite DFT implica l'operazione su un blocco dati di dimensione fissa, la sequenza di input è suddivisa in diversi blocchi dati di dimensione fissa prima dell'elaborazione.

I blocchi successivi vengono quindi elaborati uno alla volta ei risultati vengono combinati per produrre il risultato netto.

Poiché la convoluzione viene eseguita dividendo la lunga sequenza di input in diverse sezioni di dimensioni fisse, viene chiamata convoluzione sezionata. Una lunga sequenza di input viene segmentata in blocchi di dimensioni fisse, prima dell'elaborazione del filtro FIR.

Vengono utilizzati due metodi per valutare la convoluzione discreta:

• Overlap-save method

• Overlap-add method

Metodo di salvataggio sovrapposto

Overlap-save è il nome tradizionale di un modo efficiente per valutare la convoluzione discreta tra un segnale molto lungo x (n) e un filtro a risposta all'impulso finito (FIR) h (n). Di seguito sono riportati i passaggi del metodo di salvataggio Sovrapposizione:

Sia la lunghezza del blocco dati di ingresso = N = L + M-1. Pertanto, lunghezza DFT e IDFT = N. Ciascun blocco di dati trasporta i punti dati M-1 del blocco precedente seguito da L nuovi punti dati per formare una sequenza di dati di lunghezza N = L + M-1.

• Innanzitutto, viene calcolato il DFT a N punti per ciascun blocco di dati.

• Aggiungendo (L-1) zeri, la risposta all'impulso del filtro FIR viene aumentata in lunghezza e il punto N DFT viene calcolato e memorizzato.

• Moltiplicazione di due DFT a N punti H (k) e X _m (k): Y ′ _m (k) = H (k). X _m (k), dove K = 0,1,2,… N-1

• Quindi, IDFT [Y ′ _m ((k)] = y ′ ((n) = [y ′ _m (0), y ′ _m (1), y ′ _m (2), ....... y ' _m (m-1), y' _m (m), ....... y ' _m (N-1)]

  (qui, N-1 = L + M-2)

• I primi punti M-1 sono danneggiati a causa dell'aliasing e quindi vengono scartati perché il record di dati è di lunghezza N.

• Gli ultimi punti L sono esattamente gli stessi come risultato della convoluzione, quindi

  y ′ _m (n) = y _m (n) dove n = M, M + 1,…. N-1

• Per evitare l'aliasing, gli ultimi elementi M-1 di ciascun record di dati vengono salvati e questi punti vengono riportati al record successivo e diventano i ^primi elementi M-1.

• Il risultato di IDFT, dove vengono evitati i primi M-1 Punti, per annullare l'aliasing ei restanti punti L costituiscono il risultato desiderato come quello di una convoluzione lineare.

Metodo di aggiunta sovrapposizione

Di seguito sono riportati i passaggi per scoprire la convoluzione discreta utilizzando il metodo Overlap -

Lascia che la dimensione del blocco di dati di input sia L. Pertanto, la dimensione di DFT e IDFT: N = L + M-1

• Ogni blocco di dati viene aggiunto all'ultimo con zeri M-1.

• Calcola DFT a N punti.

• Si moltiplicano due DFT a N punti: Y _m (k) = H (k). X _m (k), dove k = 0 ,, 1,2,…., N-1

• IDFT [Y _m (k)] produce blocchi di lunghezza N che non sono influenzati dall'aliasing poiché la dimensione di DFT è N = L + M-1 e aumenta la lunghezza delle sequenze a N punti aggiungendo M-1 zeri a ciascuno bloccare.

• Gli ultimi punti M-1 di ogni blocco devono essere sovrapposti e aggiunti ai primi punti M-1 del blocco successivo.

  (motivo: ogni blocco dati termina con M-1 zeri)

  Quindi, questo metodo è noto come metodo di sovrapposizione-aggiunta. Quindi, otteniamo -

  y (n) = {y ₁ (0), y ₁ (1), y ₁ (2), ... .., y ₁ (L-1), y ₁ (L) + y ₂ (0), y ₁ (L + 1) + y ₂ (1), ... ... .., y ₁ (N-1) + y ₂ (M-1), y ₂ (M), ... .. . ... ... ...}

DCT (Discrete Cosine Transform) è una sequenza di input N x (n), 0≤n≤N-1, come trasformazione lineare o combinazione di esponenziali complessi. Di conseguenza, i coefficienti DFT sono in generale complessi anche se x (n) è reale.

Supponiamo di provare a trovare una trasformazione ortogonale che ha una struttura N × N che esprime una sequenza reale x (n) come combinazione lineare della sequenza del coseno. Lo sappiamo già -

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$

E $x(n) = \frac{1}{N}\sum_{k = 0}^{N-1}x(k)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$

Ciò è possibile se la sequenza di N punti x (n) è reale e pari. Quindi,$x(n) = x(N-n),0\leq n \leq (N-1)$. La stessa DFT risultante è reale e uniforme. Queste cose rendono chiaro che potremmo eventualmente congegnare una trasformata discreta del coseno, per qualsiasi sequenza reale di N punti, prendendo il punto 2N DFT di una "estensione pari" della sequenza.

DCT è, fondamentalmente, utilizzato nell'elaborazione di immagini e parlato. Viene anche utilizzato per la compressione di immagini e segnali vocali.

$DFT[s(n)] = S(k) = \sum_{n = 0}^{2N-1}s(n)W_{2N}^{nk},\quad where\quad 0\leq k \leq 2N-1$

$S(k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)W_{2N}^{nk}+\displaystyle\sum\limits_{n = N}^{2N-1}x(2N-n-1)W_{2N}^{nk};\quad where\quad 0\leq k\leq 2N-1$

$\Rightarrow S(k) = W_{2N}^{-k/2}+\sum_{n = 0}^{N-1}x(n) [W_{2N}^{nk}W_{2N}^{k/2}+W_{2N}^{-nk}W_{2N}^{-k/2}];\quad where\quad 0\leq k\leq 2N-1$

$\Rightarrow S(k) = W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{N}(n+\frac{1}{2})k];\quad where\quad 0\leq k\leq 2N-1$

DCT è definito da,

$V(k) = 2\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{2}(n+\frac{1}{2})k]\quad where\quad 0\leq k\leq N-1$

$\Rightarrow V(k) = W_{2N}^{\frac{k}{2}}S(k)\quad or\quad S(k) = W_{2N}^{\frac{k}{2}}V(k),\quad where\quad 0\leq k\leq N-1$

$\Rightarrow V(k) = 2R[W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)W_{2N}^{nk}],\quad where\quad 0\leq k\leq N-1$

Esempio 1

Verifica il teorema di Parseval della sequenza $x(n) = \frac{1^n}{4}u(n)$

Solution - $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$

LHS $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2$

$= \displaystyle\sum\limits_{-\infty}^{\infty}x(n)x^*(n)$

$= \displaystyle\sum\limits_{-\infty}^\infty(\frac{1}{4})^{2n}u(n) = \frac{1}{1-\frac{1}{16}} = \frac{16}{15}$

RHS $X(e^{j\omega}) = \frac{1}{1-\frac{1}{4}e-j\omega} = \frac{1}{1-0.25\cos \omega+j0.25\sin \omega}$

$\Longleftrightarrow X^*(e^{j\omega}) = \frac{1}{1-0.25\cos \omega-j0.25\sin \omega}$

Calcolare, $X(e^{j\omega}).X^*(e^{j\omega})$

$= \frac{1}{(1-0.25\cos \omega)^2+(0.25\sin \omega)^2} = \frac{1}{1.0625-0.5\cos \omega}$

$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega$

$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega = 16/15$

Possiamo vederlo, LHS = RHS. (Quindi dimostrato)

Esempio 2

Calcola il DFT a N punti di $x(n) = 3\delta (n)$

Solution - Lo sappiamo,

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$

$= \displaystyle\sum\limits_{n = 0}^{N-1}3\delta(n)e^{\frac{j2\Pi kn}{N}}$

$ = 3\delta (0)\times e^0 = 1$

Così,$x(k) = 3,0\leq k\leq N-1$... Ans.

Esempio 3

Calcola il DFT a N punti di $x(n) = 7(n-n_0)$

Solution - Lo sappiamo,

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$

Sostituendo il valore di x (n),

$\displaystyle\sum\limits_{n = 0}^{N-1}7\delta (n-n_0)e^{-\frac{j2\Pi kn}{N}}$

$= e^{-kj14\Pi kn_0/N}$... Ans

Nei metodi DFT precedenti, abbiamo visto che la parte computazionale è troppo lunga. Vogliamo ridurlo. Questo può essere fatto tramite FFT o trasformata di Fourier veloce. Quindi, possiamo dire che FFT non è altro che il calcolo della trasformata di Fourier discreta in un formato algoritmico, in cui la parte computazionale sarà ridotta.

Il vantaggio principale di avere FFT è che attraverso di esso, possiamo progettare i filtri FIR. Matematicamente, la FFT può essere scritta come segue;

$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$

Facciamo un esempio per capirlo meglio. Abbiamo considerato otto punti denominati da$x_0\quad to\quad x_7$. Sceglieremo i termini pari in un gruppo e i termini dispari nell'altro. La vista schematica di quanto sopra è stata mostrata di seguito:

Qui, i punti x ₀ , x ₂ , x ₄ e x ₆ sono stati raggruppati in una categoria e, analogamente, i punti x ₁ , x ₃ , x ₅ e x ₇ sono stati inseriti in un'altra categoria. Ora possiamo crearli ulteriormente in un gruppo di due e procedere con il calcolo. Ora, vediamo come questi due ulteriori due aiutano nel calcolo.

$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$

$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$

$= G[k]+H[k]\times W_N^k$

Inizialmente, abbiamo preso una sequenza di otto punti, ma in seguito l'abbiamo divisa in due parti G [k] e H [k]. G [k] sta per la parte pari mentre H [k] sta per la parte dispari. Se vogliamo realizzarlo attraverso un diagramma, allora può essere mostrato come di seguito -

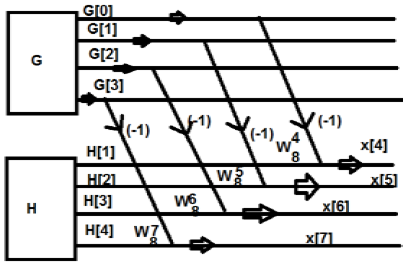
Dalla figura sopra, possiamo vederlo

$W_8^4 = -1$

$W_8^5 = -W_8^1$

$W_8^6 = -W_8^2$

$W_8^7 = -W_8^3$

Allo stesso modo, i valori finali possono essere scritti come segue:

$G[0]-H[0] = x[4]$

$G[1]-W_8^1H[1] = x[5]$

$G[2]-W_8^2H[2] = x[6]$

$G[1]-W_8^3H[3] = x[7]$

Quella sopra è una serie periodica. Lo svantaggio di questo sistema è che K non può essere rotto oltre i 4 punti. Ora analizziamo ulteriormente quanto sopra. Otterremo le strutture qualcosa di simile

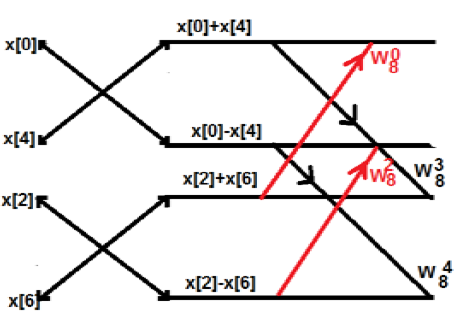
Esempio

Considera la sequenza x [n] = {2,1, -1, -3,0,1,2,1}. Calcola la FFT.

Solution - La sequenza data è x [n] = {2,1, -1, -3,0,1,2,1}

Disporre i termini come mostrato di seguito;

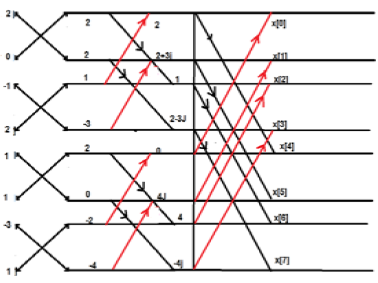
Questo uso efficiente della memoria è importante per progettare hardware veloce per calcolare la FFT. Il termine calcolo sul posto viene utilizzato per descrivere questo utilizzo della memoria.

Decimazione in sequenza temporale

In questa struttura, rappresentiamo tutti i punti in formato binario, cioè in 0 e 1. Quindi, invertiamo quelle strutture. La sequenza che otteniamo dopo è nota come sequenza di inversione di bit. Questo è anche noto come decimazione in sequenza temporale. Il calcolo sul posto di un DFT a otto punti viene mostrato in un formato tabulare come mostrato di seguito -

PUNTI	FORMATO BINARIO	INVERSIONE	PUNTI EQUIVALENTI
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

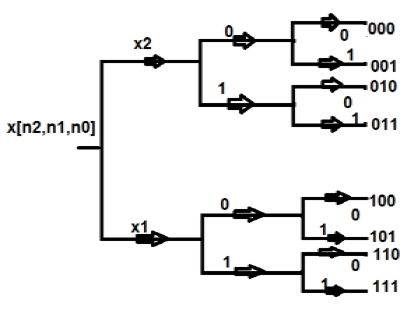
Decimazione in sequenza di frequenza

Oltre alla sequenza temporale, una sequenza N punti può anche essere rappresentata in frequenza. Prendiamo una sequenza di quattro punti per capirla meglio.

Lascia che sia la sequenza $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. Raggrupperemo due punti in un gruppo, inizialmente. Matematicamente, questa sequenza può essere scritta come;

$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$

Ora creiamo un gruppo di sequenza numero da 0 a 3 e un altro gruppo di sequenza da 4 a 7. Ora, matematicamente questo può essere mostrato come;

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$

Sostituiamo n con r, dove r = 0, 1, 2 ... (N / 2-1). Matematicamente,

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$

Prendiamo inizialmente i primi quattro punti (x [0], x [1], x [2], x [3]) e proviamo a rappresentarli matematicamente come segue:

$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$

$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$

adesso $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$

$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$

$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$

Possiamo ulteriormente suddividerlo in altre due parti, il che significa che invece di romperle come sequenza di 4 punti, possiamo suddividerle in una sequenza di 2 punti.

I filtri FIR possono essere utili nella progettazione assistita dal computer dei filtri. Facciamo un esempio e vediamo come funziona. Di seguito è riportata una figura del filtro desiderato.

Durante la progettazione del computer, suddividiamo le cifre dell'intero grafico continuo in valori discreti. Entro certi limiti, lo suddividiamo in 64, 256 o 512 (e così via) numero di parti aventi grandezze discrete.

Nell'esempio sopra, abbiamo preso i limiti tra -π e + π. Lo abbiamo diviso in 256 parti. I punti possono essere rappresentati come H (0), H (1), ... fino a H (256). Qui applichiamo l'algoritmo IDFT e questo ci darà caratteristiche di fase lineari.

A volte, potremmo essere interessati a un particolare ordine di filtro. Diciamo che vogliamo realizzare il progetto sopra dato attraverso ^il filtro di 9 ^° ordine. Quindi, prendiamo i valori del filtro come h0, h1, h2… .h9. Matematicamente, può essere mostrato come di seguito

$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$

Dove c'è un gran numero di dislocazioni, prendiamo il massimo dei punti.

Ad esempio, nella figura sopra, c'è un improvviso calo di pendenza tra i punti B e C.Quindi, proviamo a prendere valori più discreti a questo punto, ma c'è una pendenza costante tra il punto C e D. Là prendiamo minor numero di valori discreti.

Per progettare il filtro sopra, seguiamo il processo di minimizzazione come segue;

$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$

$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$

Allo stesso modo,

$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$

Rappresentando l'equazione di cui sopra in forma di matrice, abbiamo:

$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$

Prendiamo la matrice 1000 × 1 come B, la matrice 1000 × 9 come A e la matrice 9 × 1 come $\hat{h}$.

Quindi, per risolvere la matrice sopra, scriveremo

$\hat{h} = [A^TA]^{-1}A^{T}B$

$= [A^{*T}A]^{-1}A^{*T}B$

dove A ^* rappresenta il complesso coniugato della matrice A.