Matematica discreta - Spanning Trees
Uno spanning tree di un grafo non orientato connesso $ G $ è un albero che include in minima parte tutti i vertici di $ G $. Un grafico può avere molti spanning tree.
Esempio
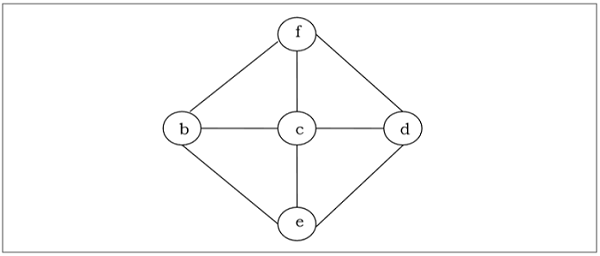
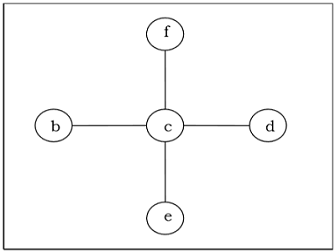
Spanning Tree minimo
Uno spanning tree con peso assegnato inferiore o uguale al peso di ogni possibile spanning tree di un grafo $ G $ pesato, connesso e non orientato, è chiamato albero di copertura minimo (MST). Il peso di uno spanning tree è la somma di tutti i pesi assegnati a ciascun bordo dello spanning tree.
Esempio
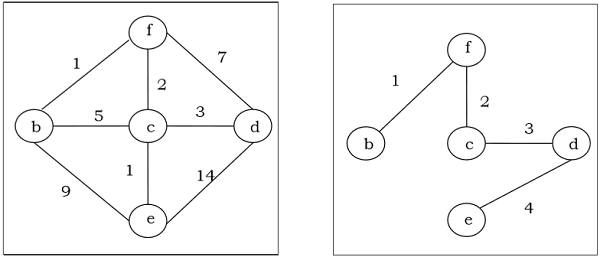
Algoritmo di Kruskal
L'algoritmo di Kruskal è un algoritmo avido che trova uno spanning tree minimo per un grafo ponderato connesso. Trova un albero di quel grafo che include ogni vertice e il peso totale di tutti i bordi dell'albero è inferiore o uguale a ogni possibile albero di copertura.
Algoritmo
Step 1 - Disporre tutti i bordi del grafico $ G (V, E) $ in ordine crescente in base al loro peso.
Step 2 - Scegli il bordo ponderato più piccolo dal grafico e controlla se forma un ciclo con lo spanning tree formato finora.
Step 3 - Se non c'è ciclo, includi questo bordo nello spanning tree altrimenti scartalo.
Step 4 - Ripetere i passaggi 2 e 3 fino a quando $ (V-1) $ numero di spigoli rimane nello spanning tree.
Problem
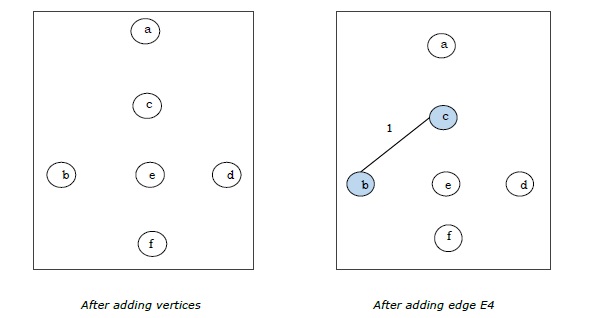
Supponiamo di voler trovare l'albero di copertura minimo per il seguente grafo G usando l'algoritmo di Kruskal.
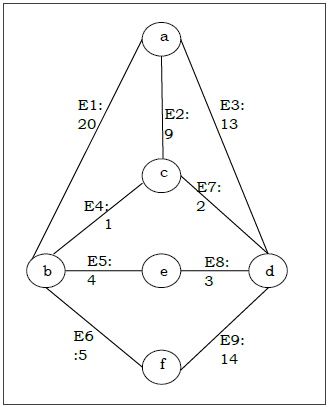
Solution
Dal grafico sopra costruiamo la seguente tabella:
| Bordo n. | Coppia di vertici | Peso del bordo |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (corrente alternata) | 9 |
| E3 | (anno Domini) | 13 |
| E4 | (avanti Cristo) | 1 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Ora riorganizzeremo la tabella in ordine crescente rispetto al peso del bordo -
| Bordo n. | Coppia di vertici | Peso del bordo |
|---|---|---|
| E4 | (avanti Cristo) | 1 |
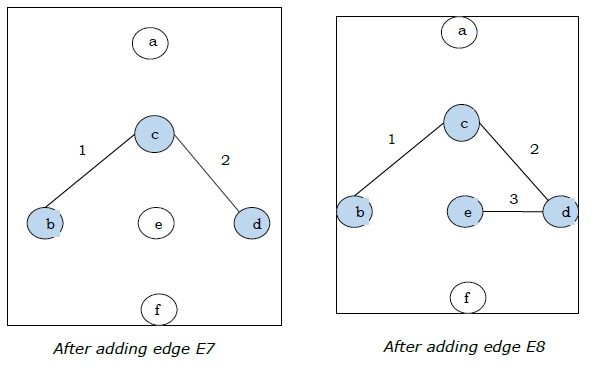
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E2 | (corrente alternata) | 9 |
| E3 | (anno Domini) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
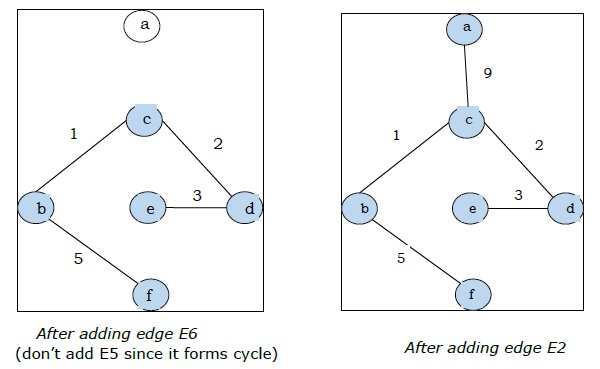
Poiché nell'ultima figura abbiamo ottenuto tutti e 5 gli archi, interrompiamo l'algoritmo e questo è lo spanning tree minimo e il suo peso totale è $ (1 + 2 + 3 + 5 + 9) = 20 $.
Algoritmo di Prim
L'algoritmo di Prim, scoperto nel 1930 dai matematici Vojtech Jarnik e Robert C. Prim, è un algoritmo avido che trova uno spanning tree minimo per un grafo ponderato connesso. Trova un albero di quel grafo che include ogni vertice e il peso totale di tutti i bordi dell'albero è inferiore o uguale a ogni possibile albero di copertura. L'algoritmo di Prim è più veloce su grafici densi.
Algoritmo
Inizializza l'albero di copertura minimo con un singolo vertice, scelto a caso dal grafico.
Ripetere i passaggi 3 e 4 fino a quando tutti i vertici sono inclusi nell'albero.
Selezionare un bordo che colleghi l'albero con un vertice non ancora nell'albero, in modo che il peso del bordo sia minimo e l'inclusione del bordo non formi un ciclo.
Aggiungi il bordo selezionato e il vertice che si collega all'albero.
Problem
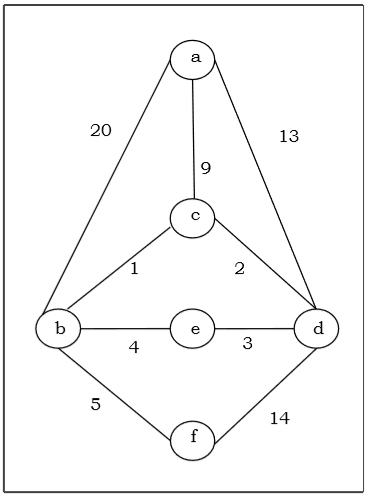
Supponiamo di voler trovare il minimo spanning tree per il seguente grafo G usando l'algoritmo di Prim.
Solution
Qui iniziamo con il vertice "a" e procediamo.
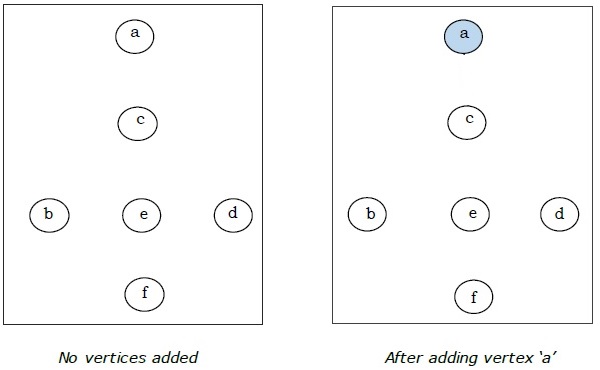
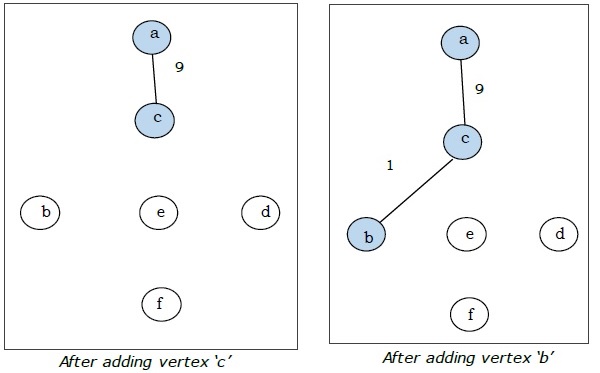
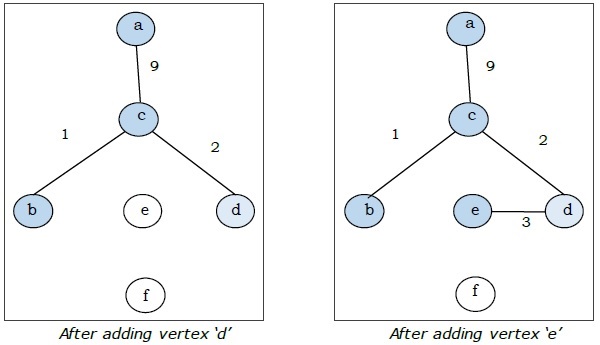
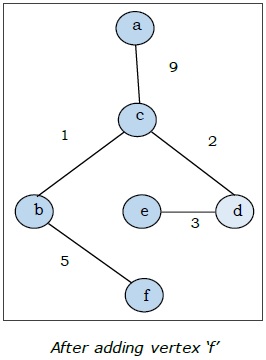
Questo è lo spanning tree minimo e il suo peso totale è $ (1 + 2 + 3 + 5 + 9) = 20 $.