Matematica discreta - Maggiori informazioni sui grafici
Colorazione del grafico
La colorazione del grafo è la procedura di assegnazione dei colori a ciascun vertice di un grafo G in modo tale che nessun vertice adiacente abbia lo stesso colore. L'obiettivo è ridurre al minimo il numero di colori durante la colorazione di un grafico. Il numero minimo di colori richiesto per colorare un grafico G è chiamato il numero cromatico di quel grafico. Il problema di colorazione dei grafici è un problema NP Complete.
Metodo per colorare un grafico
I passaggi necessari per colorare un grafo G con n numero di vertici sono i seguenti:
Step 1 - Disporre i vertici del grafico in un certo ordine.
Step 2 - Scegli il primo vertice e coloralo con il primo colore.
Step 3- Scegli il vertice successivo e coloralo con il colore con il numero più basso che non è stato colorato su alcun vertice adiacente ad esso. Se tutti i vertici adiacenti sono colorati con questo colore, assegnagli un nuovo colore. Ripeti questo passaggio finché tutti i vertici non sono colorati.
Example
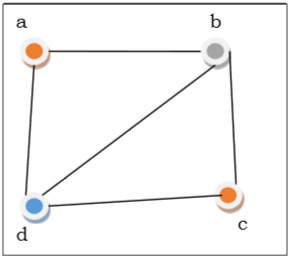
Nella figura sopra, al primo vertice $ a $ è colorato in rosso. Poiché i vertici adiacenti del vertice a sono nuovamente adiacenti, il vertice $ b $ e il vertice $ d $ sono colorati con colori diversi, rispettivamente verde e blu. Quindi il vertice $ c $ è colorato in rosso poiché nessun vertice adiacente di $ c $ è colorato in rosso. Quindi, potremmo colorare il grafico con 3 colori. Quindi, il numero cromatico del grafico è 3.
Applicazioni della colorazione dei grafi
Alcune applicazioni della colorazione dei grafici includono:
- Registrazione allocazione
- Colorazione della mappa
- Controllo grafico bipartito
- Assegnazione della frequenza radio mobile
- Fare un orario, ecc.
Attraversamento grafico
L'attraversamento del grafo è il problema di visitare tutti i vertici di un grafo in un certo ordine sistematico. Esistono principalmente due modi per attraversare un grafico.
- Ampiezza prima ricerca
- Prima ricerca in profondità
Ampiezza prima ricerca
Breadth First Search (BFS) inizia al vertice di livello 0 $ X $ del grafico $ G $. Quindi visitiamo tutti i vertici che sono vicini a $ X $. Dopo la visita, contrassegniamo i vertici come "visitati" e li posizioniamo nel livello 1. Quindi iniziamo dai vertici di livello 1 e applichiamo lo stesso metodo su ogni vertice di livello 1 e così via. L'attraversamento BFS termina quando ogni vertice del grafico è stato visitato.
BFS Algorithm
Il concetto è visitare tutti i vertici vicini prima di visitare altri vertici vicini dei vertici vicini.
Inizializza lo stato di tutti i nodi come "Pronto".
Metti il vertice di origine in una coda e cambia il suo stato in "In attesa".
Ripeti i due passaggi seguenti finché la coda non è vuota:
Rimuovere il primo vertice dalla coda e contrassegnarlo come "Visitato".
Aggiungere in coda alla coda tutti i vicini del vertice rimosso il cui stato è "Pronto". Contrassegna il loro stato come "In attesa".
Problem
Prendiamo un grafo (il vertice di origine è 'a') e applichiamo l'algoritmo BFS per scoprire l'ordine di attraversamento.
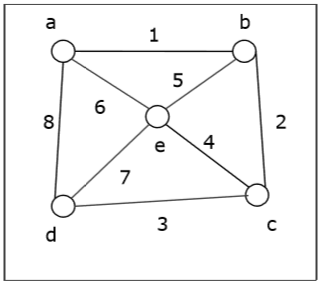
Solution -
Inizializza lo stato di tutti i vertici su "Pronto".
Metti un in coda e cambia il suo stato in "In attesa".
Rimuovere un dalla coda, contrassegnarlo come "Visitato".
Aggiungere un s’vicini a‘Pronto’stato b, d ed e fino alla fine della coda e contrassegnarli come‘attesa’.
Rimuovi b dalla coda, contrassegnalo come "Visitato", metti il suo vicino "Pronto" c alla fine della coda e contrassegna c come "In attesa".
Rimuovi d dalla coda e contrassegnalo come "Visitato". Non ha un vicino nello stato "Pronto".
Rimuovere e dalla coda e contrassegnarlo come "Visitato". Non ha un vicino nello stato "Pronto".
Rimuovere c dalla coda e contrassegnarlo come "Visitato". Non ha un vicino nello stato "Pronto".
La coda è vuota quindi fermati.
Quindi l'ordine di attraversamento è:
$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $
Gli ordini alternativi di attraversamento sono:
$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
Oppure $ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $
Oppure $ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $
Oppure $ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
Oppure $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
Application of BFS
- Trovare il percorso più breve
- Spanning tree minimo per grafo non ponderato
- Sistema di navigazione GPS
- Rilevamento dei cicli in un grafico non orientato
- Trovare tutti i nodi all'interno di un componente connesso
Complexity Analysis
Sia $ G (V, E) $ un grafico con $ | V | $ numero di vertici e $ | E | $ numero di archi. Se l'algoritmo di ricerca in base all'ampiezza visita ogni vertice nel grafico e controlla ogni bordo, la sua complessità temporale sarebbe:
$$ O (| V | + | E |). O (| E |) $$
Può variare tra $ O (1) $ e $ O (| V2 |) $
Prima ricerca in profondità
L'algoritmo Depth First Search (DFS) parte da un vertice $ v $, quindi attraversa il vertice adiacente (diciamo x) che non è stato visitato prima e contrassegna come "visitato" e prosegue con il vertice adiacente di $ x $ e presto.
Se in qualsiasi vertice, incontra che tutti i vertici adiacenti sono visitati, torna indietro finché non trova il primo vertice con un vertice adiacente che non è stato attraversato prima. Quindi, attraversa quel vertice, continua con i suoi vertici adiacenti finché non attraversa tutti i vertici visitati e deve tornare indietro di nuovo. In questo modo, attraverserà tutti i vertici raggiungibili dal vertice iniziale $ v $.
DFS Algorithm
Il concetto è quello di visitare tutti i vertici vicini di un vertice adiacente prima di visitare gli altri vertici vicini.
Inizializza lo stato di tutti i nodi come "Pronto"
Metti il vertice di origine in una pila e modifica il suo stato in "In attesa"
Ripeti i due passaggi seguenti finché lo stack non è vuoto:
Estrai il vertice superiore dalla pila e contrassegnalo come "Visitato"
Spingere in cima alla pila tutti i vicini del vertice rimosso il cui stato è "Pronto". Contrassegna il loro stato come "In attesa".
Problem
Prendiamo un grafo (il vertice di origine è 'a') e applichiamo l'algoritmo DFS per scoprire l'ordine di attraversamento.
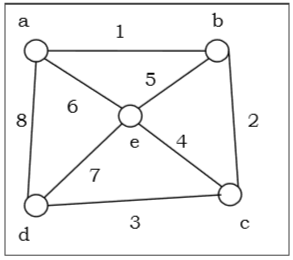
Solution
Inizializza lo stato di tutti i vertici su "Pronto".
Spingi una pila e cambia il suo stato in "In attesa".
Apri un e contrassegnalo come "Visitato".
Spingere un vicini di casa ‘s in‘Pronto’Stato e, d e B per cima alla pila e contrassegnarli come‘attesa’.
Apri b dalla pila, contrassegnalo come "Visitato", spinge il suo vicino "Pronto" c nella pila.
Estrarre c dalla pila e contrassegnarlo come "Visitato". Non ha un vicino "Pronto".
Apri d dalla pila e contrassegnalo come "Visitato". Non ha un vicino "Pronto".
Pop e dalla pila e segnare come “Visitato”. Non ha un vicino "Pronto".
Lo stack è vuoto. Quindi fermati.
Quindi l'ordine di attraversamento è:
$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $
Gli ordini alternativi di attraversamento sono:
$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $
Oppure $ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $
Oppure $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
Oppure $ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $
Oppure $ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $
Complexity Analysis
Sia $ G (V, E) $ un grafico con $ | V | $ numero di vertici e $ | E | $ numero di archi. Se l'algoritmo DFS visita ogni vertice nel grafico e controlla ogni bordo, la complessità temporale è:
$$ \ circleddash (| V | + | E |) $$
Applications
- Rilevamento del ciclo in un grafico
- Per trovare l'ordinamento topologico
- Per verificare se un grafo è bipartito
- Trovare componenti collegati
- Trovare i ponti di un grafico
- Trovare la bi-connettività nei grafici
- Risolvere il problema del Knight's Tour
- Risolvere i puzzle con una sola soluzione