MATLAB - Operatori
Un operatore è un simbolo che dice al compilatore di eseguire specifiche manipolazioni matematiche o logiche. MATLAB è progettato per funzionare principalmente su intere matrici e array. Pertanto, gli operatori in MATLAB lavorano sia su dati scalari che non scalari. MATLAB consente i seguenti tipi di operazioni elementari:
- Operatori aritmetici
- Operatori relazionali
- Operatori logici
- Operazioni bit per bit
- Imposta operazioni
Operatori aritmetici
MATLAB consente due diversi tipi di operazioni aritmetiche:
- Operazioni aritmetiche su matrici
- Operazioni aritmetiche su array
Le operazioni aritmetiche delle matrici sono le stesse definite in algebra lineare. Le operazioni sugli array vengono eseguite elemento per elemento, sia su array unidimensionali che multidimensionali.
Gli operatori di matrice e gli operatori di matrice sono differenziati dal simbolo del punto (.). Tuttavia, poiché l'operazione di addizione e sottrazione è la stessa per matrici e array, l'operatore è lo stesso per entrambi i casi. La tabella seguente fornisce una breve descrizione degli operatori:
Mostra esempi
| Sr.No. | Operatore e descrizione |
|---|---|
| 1 | + Addizione o plus unario. A + B aggiunge i valori memorizzati nelle variabili A e B. A e B devono avere la stessa dimensione, a meno che uno non sia uno scalare. Uno scalare può essere aggiunto a una matrice di qualsiasi dimensione. |
| 2 | - Sottrazione o meno unario. AB sottrae il valore di B da A. A e B devono avere la stessa dimensione, a meno che uno non sia uno scalare. Uno scalare può essere sottratto da una matrice di qualsiasi dimensione. |
| 3 | * Moltiplicazione di matrici. C = A * B è il prodotto algebrico lineare delle matrici A e B. Più precisamente,
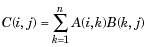
Per A e B non scalari, il numero di colonne di A deve essere uguale al numero di righe di B. Uno scalare può moltiplicare una matrice di qualsiasi dimensione. |
| 4 | .* Moltiplicazione di array. A. * B è il prodotto elemento per elemento degli array A e B. A e B devono avere la stessa dimensione, a meno che uno di essi non sia uno scalare. |
| 5 | / Divisione destra con barra o matrice. B / A è più o meno uguale a B * inv (A). Più precisamente, B / A = (A '\ B') '. |
| 6 | ./ Array divisione destra. A./B è la matrice con gli elementi A (i, j) / B (i, j). A e B devono avere la stessa dimensione, a meno che uno di essi non sia uno scalare. |
| 7 | \ Barra rovesciata o divisione a sinistra della matrice. Se A è una matrice quadrata, A \ B è più o meno uguale a inv (A) * B, tranne per il fatto che è calcolato in modo diverso. Se A è un n-da-n matrice e B è un vettore colonna con n componenti, o una matrice con diversi tali colonne, allora X = A \ B è la soluzione dell'equazione AX = B . Viene visualizzato un messaggio di avviso se A è ridimensionato in modo errato o quasi singolare. |
| 8 | .\ Divisione sinistra matrice. A. \ B è la matrice con gli elementi B (i, j) / A (i, j). A e B devono avere la stessa dimensione, a meno che uno di essi non sia uno scalare. |
| 9 | ^ Potere della matrice. X ^ p è X alla potenza p, se p è uno scalare. Se p è un numero intero, la potenza viene calcolata per quadratura ripetuta. Se il numero intero è negativo, X viene invertito per primo. Per altri valori di p, il calcolo coinvolge autovalori e autovettori, tali che se [V, D] = eig (X), allora X ^ p = V * D. ^ p / V. |
| 10 | .^ Potenza array. A. ^ B è la matrice con gli elementi A (i, j) alla potenza B (i, j). A e B devono avere la stessa dimensione, a meno che uno di essi non sia uno scalare. |
| 11 | ' Trasposizione della matrice. A 'è la trasposizione algebrica lineare di A. Per matrici complesse, questa è la trasposizione coniugata complessa. |
| 12 | .' Trasposizione di array. UN.' è la trasposizione dell'array di A. Per matrici complesse, ciò non implica la coniugazione. |
Operatori relazionali
Gli operatori relazionali possono anche lavorare su dati scalari e non scalari. Gli operatori relazionali per gli array eseguono confronti elemento per elemento tra due array e restituiscono un array logico della stessa dimensione, con gli elementi impostati su 1 logico (vero) dove la relazione è vera e gli elementi impostati su 0 logico (falso) dove si trova non.
La tabella seguente mostra gli operatori relazionali disponibili in MATLAB -
Mostra esempi
| Sr.No. | Operatore e descrizione |
|---|---|
| 1 | < Meno di |
| 2 | <= Minore o uguale a |
| 3 | > Più grande di |
| 4 | >= Maggiore o uguale a |
| 5 | == Uguale a |
| 6 | ~= Non uguale a |
Operatori logici
MATLAB offre due tipi di operatori logici e funzioni:
Dal punto di vista degli elementi: questi operatori operano sugli elementi corrispondenti degli array logici.
Cortocircuito: questi operatori operano su espressioni logiche e scalari.
Gli operatori logici per elemento operano elemento per elemento su array logici. I simboli &, | e ~ sono gli operatori della matrice logica AND, OR e NOT.
Gli operatori logici di cortocircuito consentono il cortocircuito sulle operazioni logiche. I simboli && e || sono gli operatori logici di cortocircuito AND e OR.
Mostra esempi
Operazioni bit per bit
Gli operatori bit per bit lavorano sui bit ed eseguono operazioni bit per bit. Le tabelle di verità per &, | e ^ sono le seguenti:
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Assumiamo se A = 60; e B = 13; Ora in formato binario saranno i seguenti:
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A | B = 0011 1101
A ^ B = 0011 0001
~ A = 1100 0011
MATLAB fornisce varie funzioni per operazioni bit per bit come operazioni "bit per bit e", "bit per bit o" e "non per bit", operazioni di spostamento, ecc.
La tabella seguente mostra le operazioni bit per bit comunemente utilizzate:
Mostra esempi
| Funzione | Scopo |
|---|---|
| bitand (a, b) | AND bit per bit di interi a e b |
| bitcmp (a) | Bit-wise complemento di un file |
| bitget (a, pos) | Ottieni bit nella posizione pos specificata , nell'array intero a |
| bitor (a, b) | OR bit per bit di interi a e b |
| bitset (a, pos) | Imposta il bit nella posizione specifica pos di a |
| bitshift (a, k) | Restituisce uno spostato a sinistra di k bit, equivalente a moltiplicare per 2 k . I valori negativi di k corrispondono allo spostamento dei bit a destra o alla divisione per 2 | k | e arrotondando al numero intero più vicino verso l'infinito negativo. Eventuali bit di overflow vengono troncati. |
| bitxor (a, b) | XOR bit per bit di interi a e b |
| swapbytes | Scambia l'ordine dei byte |
Imposta operazioni
MATLAB fornisce varie funzioni per operazioni sugli insiemi, come unione, intersezione e test per l'appartenenza agli insiemi, ecc.
La tabella seguente mostra alcune operazioni di impostazione comunemente utilizzate:
Mostra esempi
| Sr.No. | Descrizione della funzione |
|---|---|
| 1 | intersect(A,B) Imposta l'intersezione di due array; restituisce i valori comuni sia ad A che a B. I valori restituiti sono ordinati. |
| 2 | intersect(A,B,'rows') Tratta ogni riga di A e ogni riga di B come entità singole e restituisce le righe comuni sia ad A che a B. Le righe della matrice restituita sono ordinate. |
| 3 | ismember(A,B) Restituisce un array della stessa dimensione di A, contenente 1 (vero) dove gli elementi di A si trovano in B. Altrove, restituisce 0 (falso). |
| 4 | ismember(A,B,'rows') Tratta ogni riga di A e ogni riga di B come entità singole e restituisce un vettore contenente 1 (vero) dove le righe della matrice A sono anche righe di B. Altrove, restituisce 0 (falso). |
| 5 | issorted(A) Restituisce 1 logico (vero) se gli elementi di A sono ordinati e 0 logico (falso) in caso contrario. L'input A può essere un vettore o un array di celle N per 1 o 1 per N di stringhe.A is considered to be sorted if A e l'output di sort (A) sono uguali. |
| 6 | issorted(A, 'rows') Restituisce 1 logico (vero) se le righe della matrice bidimensionale A sono ordinate e 0 logico (falso) in caso contrario. Matrix A is considered to be sorted if A e l'output di sortrows (A) sono uguali. |
| 7 | setdiff(A,B) Imposta la differenza di due array; restituisce i valori in A che non sono in B. I valori nella matrice restituita sono ordinati. |
| 8 | setdiff(A,B,'rows') Tratta ogni riga di A e ogni riga di B come singole entità e restituisce le righe di A che non sono in B. Le righe della matrice restituita sono ordinate. L'opzione "righe" non supporta gli array di celle. |
| 9 | setxor Imposta l'OR esclusivo di due array |
| 10 | union Imposta l'unione di due array |
| 11 | unique Valori univoci in matrice |