MATLAB - Guida rapida
MATLAB (Matrix Laboratory) è un linguaggio di programmazione di alto livello di quarta generazione e un ambiente interattivo per il calcolo numerico, la visualizzazione e la programmazione.
MATLAB è sviluppato da MathWorks.
Consente manipolazioni di matrici; rappresentazione grafica di funzioni e dati; implementazione di algoritmi; creazione di interfacce utente; interfacciamento con programmi scritti in altri linguaggi, inclusi C, C ++, Java e FORTRAN; analizzare i dati; sviluppare algoritmi; e creare modelli e applicazioni.
Ha numerosi comandi incorporati e funzioni matematiche che ti aiutano nei calcoli matematici, nella generazione di grafici e nell'esecuzione di metodi numerici.
Il potere della matematica computazionale di MATLAB
MATLAB è utilizzato in ogni aspetto della matematica computazionale. Di seguito sono riportati alcuni calcoli matematici di uso comune in cui viene utilizzato più comunemente:
- Trattare con matrici e array
- Stampa e grafica 2-D e 3-D
- Algebra lineare
- Equazioni algebriche
- Funzioni non lineari
- Statistics
- Analisi dei dati
- Calcolo ed equazioni differenziali
- Calcoli numerici
- Integration
- Transforms
- Raccordo a curva
- Varie altre funzioni speciali
Caratteristiche di MATLAB
Di seguito sono riportate le caratteristiche di base di MATLAB:
È un linguaggio di alto livello per il calcolo numerico, la visualizzazione e lo sviluppo di applicazioni.
Fornisce inoltre un ambiente interattivo per l'esplorazione iterativa, la progettazione e la risoluzione dei problemi.
Fornisce una vasta libreria di funzioni matematiche per algebra lineare, statistica, analisi di Fourier, filtri, ottimizzazione, integrazione numerica e risoluzione di equazioni differenziali ordinarie.
Fornisce grafica incorporata per la visualizzazione dei dati e strumenti per la creazione di grafici personalizzati.
L'interfaccia di programmazione di MATLAB fornisce strumenti di sviluppo per migliorare la manutenibilità della qualità del codice e massimizzare le prestazioni.
Fornisce strumenti per la creazione di applicazioni con interfacce grafiche personalizzate.
Fornisce funzioni per l'integrazione di algoritmi basati su MATLAB con applicazioni e linguaggi esterni come C, Java, .NET e Microsoft Excel.
Usi di MATLAB
MATLAB è ampiamente utilizzato come strumento di calcolo nella scienza e nell'ingegneria che comprende i campi della fisica, della chimica, della matematica e di tutti i flussi di ingegneria. Viene utilizzato in una vasta gamma di applicazioni, tra cui:
- Elaborazione del segnale e comunicazioni
- Elaborazione di immagini e video
- Sistemi di controllo
- Test e misurazioni
- Finanza computazionale
- Biologia computazionale
Configurazione dell'ambiente locale
La configurazione dell'ambiente MATLAB è questione di pochi clic. Il programma di installazione può essere scaricato da qui .
MathWorks fornisce il prodotto con licenza, una versione di prova e anche una versione per studenti. Devi accedere al sito e attendere un po 'per la loro approvazione.
Dopo aver scaricato il programma di installazione, il software può essere installato con pochi clic.
Capire l'ambiente MATLAB
L'IDE di sviluppo MATLAB può essere avviato dall'icona creata sul desktop. La finestra di lavoro principale in MATLAB si chiama desktop. Quando MATLAB viene avviato, il desktop appare nel suo layout predefinito -
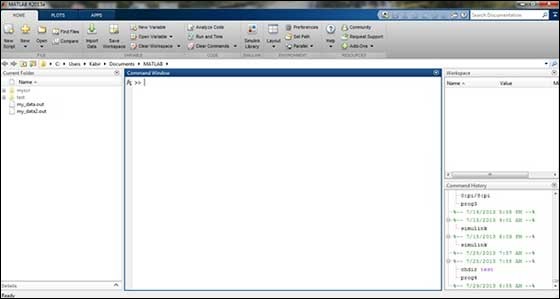
Il desktop ha i seguenti pannelli:
Current Folder - Questo pannello consente di accedere alle cartelle e ai file del progetto.
Command Window- Questa è l'area principale in cui è possibile immettere i comandi dalla riga di comando. È indicato dal prompt dei comandi (>>).
Workspace - L'area di lavoro mostra tutte le variabili create e / o importate dai file.
Command History - Questo pannello mostra o restituisce i comandi immessi nella riga di comando.


Imposta GNU Octave
Se desideri utilizzare Octave sulla tua macchina (Linux, BSD, OS X o Windows), scarica gentilmente l'ultima versione da Download GNU Octave . È possibile controllare le istruzioni di installazione fornite per la macchina.
L'ambiente MATLAB si comporta come un calcolatore super complesso. È possibile immettere comandi al prompt dei comandi >>.
MATLAB è un ambiente interpretato. In altre parole, dai un comando e MATLAB lo esegue immediatamente.
Pratica pratica
Digita un'espressione valida, ad esempio,
5 + 5E premere INVIO
Quando fai clic sul pulsante Esegui o digiti Ctrl + E, MATLAB lo esegue immediatamente e il risultato restituito è -
ans = 10Prendiamo alcuni altri esempi:
3 ^ 2 % 3 raised to the power of 2Quando fai clic sul pulsante Esegui o digiti Ctrl + E, MATLAB lo esegue immediatamente e il risultato restituito è -
ans = 9Un altro esempio,
sin(pi /2) % sine of angle 90oQuando fai clic sul pulsante Esegui o digiti Ctrl + E, MATLAB lo esegue immediatamente e il risultato restituito è -
ans = 1Un altro esempio,
7/0 % Divide by zeroQuando fai clic sul pulsante Esegui o digiti Ctrl + E, MATLAB lo esegue immediatamente e il risultato restituito è -
ans = Inf
warning: division by zeroUn altro esempio,
732 * 20.3Quando fai clic sul pulsante Esegui o digiti Ctrl + E, MATLAB lo esegue immediatamente e il risultato restituito è -
ans = 1.4860e+04MATLAB fornisce alcune espressioni speciali per alcuni simboli matematici, come pi per π, Inf per ∞, i (ej) per √-1 ecc. Nan sta per "not a number".
Uso del punto e virgola (;) in MATLAB
Il punto e virgola (;) indica la fine dell'istruzione. Tuttavia, se desideri sopprimere e nascondere l'output MATLAB per un'espressione, aggiungi un punto e virgola dopo l'espressione.
Per esempio,
x = 3;
y = x + 5Quando fai clic sul pulsante Esegui o digiti Ctrl + E, MATLAB lo esegue immediatamente e il risultato restituito è -
y = 8Aggiunta di commenti
Il simbolo della percentuale (%) viene utilizzato per indicare una riga di commento. Per esempio,
x = 9 % assign the value 9 to xPuoi anche scrivere un blocco di commenti utilizzando gli operatori di commenti di blocco% {e%}.
L'editor MATLAB include strumenti e voci del menu contestuale per aiutarti ad aggiungere, rimuovere o modificare il formato dei commenti.
Operatori e caratteri speciali comunemente usati
MATLAB supporta i seguenti operatori e caratteri speciali di uso comune:
| Operatore | Scopo |
|---|---|
| + | Più; operatore di addizione. |
| - | Meno; operatore di sottrazione. |
| * | Operatore di moltiplicazione scalare e matriciale. |
| .* | Operatore di moltiplicazione di array. |
| ^ | Operatore di esponenziazione scalare e matrice. |
| .^ | Operatore di esponenziazione di array. |
| \ | Operatore di divisione a sinistra. |
| / | Operatore di divisione a destra. |
| .\ | Operatore di divisione sinistra della matrice. |
| ./ | Operatore di divisione a destra dell'array. |
| : | Colon; genera elementi regolarmente distanziati e rappresenta un'intera riga o colonna. |
| ( ) | Parentesi; racchiude argomenti di funzione e indici di array; sovrascrive la precedenza. |
| [ ] | Parentesi; racchiude gli elementi dell'array. |
| . | Punto decimale. |
| … | Ellissi; operatore di continuazione della riga |
| , | Virgola; separa le istruzioni e gli elementi in una riga |
| ; | Punto e virgola; separa le colonne e sopprime la visualizzazione. |
| % | Segno di percentuale; designa un commento e specifica la formattazione. |
| _ | Segnale di citazione e operatore di trasposizione. |
| ._ | Operatore di trasposizione non coniugato. |
| = | Operatore di assegnazione. |
Variabili speciali e costanti
MATLAB supporta le seguenti variabili e costanti speciali:
| Nome | Senso |
|---|---|
| ans | Risposta più recente. |
| eps | Precisione della precisione in virgola mobile. |
| i,j | L'unità immaginaria √-1. |
| Inf | Infinito. |
| NaN | Risultato numerico indefinito (non un numero). |
| pi | Il numero π |
Denominazione delle variabili
I nomi delle variabili sono costituiti da una lettera seguita da un numero qualsiasi di lettere, cifre o trattini bassi.
MATLAB è case-sensitive.
I nomi delle variabili possono essere di qualsiasi lunghezza, tuttavia, MATLAB utilizza solo i primi N caratteri, dove N è dato dalla funzione namelengthmax.
Salvare il tuo lavoro
Il save viene utilizzato per salvare tutte le variabili nell'area di lavoro, come file con estensione .mat, nella directory corrente.
Per esempio,
save myfilePuoi ricaricare il file in qualsiasi momento utilizzando l'estensione load comando.
load myfileNell'ambiente MATLAB, ogni variabile è un array o una matrice.
Puoi assegnare variabili in modo semplice. Per esempio,
x = 3 % defining x and initializing it with a valueMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
x = 3Crea una matrice 1 per 1 denominata x e memorizza il valore 3 nel suo elemento. Controlliamo un altro esempio,
x = sqrt(16) % defining x and initializing it with an expressionMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
x = 4Si prega di notare che -
Una volta inserita una variabile nel sistema, è possibile farvi riferimento in un secondo momento.
Le variabili devono avere valori prima di essere utilizzate.
Quando un'espressione restituisce un risultato che non è assegnato a nessuna variabile, il sistema lo assegna a una variabile denominata ans, che può essere utilizzata in seguito.
Per esempio,
sqrt(78)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 8.8318Puoi usare questa variabile ans -
sqrt(78);
9876/ansMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 1118.2Diamo un'occhiata a un altro esempio:
x = 7 * 8;
y = x * 7.89MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
y = 441.84Assegnazioni multiple
Puoi avere più compiti sulla stessa riga. Per esempio,
a = 2; b = 7; c = a * bMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
c = 14Ho dimenticato le variabili!
Il who Il comando mostra tutti i nomi delle variabili che hai usato.
whoMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
Your variables are:
a ans b cIl whos Il comando mostra poco di più sulle variabili -
- Variabili attualmente in memoria
- Tipo di ciascuna variabile
- Memoria assegnata a ciascuna variabile
- Che si tratti di variabili complesse o meno
whosMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
Attr Name Size Bytes Class
==== ==== ==== ==== =====
a 1x1 8 double
ans 1x70 757 cell
b 1x1 8 double
c 1x1 8 double
Total is 73 elements using 781 bytesIl clear Il comando elimina tutte (o le variabili specificate) dalla memoria.
clear x % it will delete x, won't display anything
clear % it will delete all variables in the workspace
% peacefully and unobtrusivelyAssegnazioni lunghe
Le assegnazioni lunghe possono essere estese a un'altra riga utilizzando i puntini di sospensione (...). Per esempio,
initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity + acceleration * timeMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
final_velocity = 196Il formato Command
Per impostazione predefinita, MATLAB visualizza i numeri con quattro valori di posizione decimale. Questo è noto comeshort format.
Tuttavia, se si desidera una maggiore precisione, è necessario utilizzare l'estensione format comando.
Il format long Il comando visualizza 16 cifre dopo i decimali.
Ad esempio:
format long
x = 7 + 10/3 + 5 ^ 1.2MATLAB eseguirà l'istruzione precedente e restituirà il seguente risultato -
x = 17.2319816406394Un altro esempio,
format short
x = 7 + 10/3 + 5 ^ 1.2MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
x = 17.232Il format bankIl comando arrotonda i numeri a due cifre decimali. Per esempio,
format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
weekly_wage = 1064.70MATLAB visualizza numeri grandi utilizzando la notazione esponenziale.
Il format short e il comando consente la visualizzazione in forma esponenziale con quattro cifre decimali più l'esponente.
Per esempio,
format short e
4.678 * 4.9MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 2.2922e+01Il format long eil comando consente la visualizzazione in forma esponenziale con quattro cifre decimali più l'esponente. Per esempio,
format long e
x = piMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
x = 3.141592653589793e+00Il format ratfornisce l'espressione razionale più vicina risultante da un calcolo. Per esempio,
format rat
4.678 * 4.9MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 34177/1491Creazione di vettori
Un vettore è una matrice unidimensionale di numeri. MATLAB consente di creare due tipi di vettori:
- Vettori di riga
- Vettori di colonna
Row vectors vengono creati racchiudendo l'insieme di elementi tra parentesi quadre, utilizzando lo spazio o la virgola per delimitare gli elementi.
Per esempio,
r = [7 8 9 10 11]MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
r =
7 8 9 10 11Un altro esempio,
r = [7 8 9 10 11];
t = [2, 3, 4, 5, 6];
res = r + tMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
res =
9 11 13 15 17Column vectors vengono creati racchiudendo l'insieme di elementi tra parentesi quadre, utilizzando il punto e virgola (;) per delimitare gli elementi.
c = [7; 8; 9; 10; 11]MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
c =
7
8
9
10
11Creazione di matrici
Una matrice è una matrice bidimensionale di numeri.
In MATLAB, una matrice viene creata inserendo ogni riga come una sequenza di elementi separati da spazi o virgole e la fine di una riga è delimitata da un punto e virgola. Ad esempio, creiamo una matrice 3 per 3 come -
m = [1 2 3; 4 5 6; 7 8 9]MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
m =
1 2 3
4 5 6
7 8 9MATLAB è un programma interattivo per il calcolo numerico e la visualizzazione dei dati. È possibile immettere un comando digitandolo al prompt di MATLAB ">>" nel fileCommand Window.
In questa sezione, forniremo elenchi di comandi MATLAB generali di uso comune.
Comandi per la gestione di una sessione
MATLAB fornisce vari comandi per la gestione di una sessione. La tabella seguente fornisce tutti questi comandi:
| Comando | Scopo |
|---|---|
| clc | Cancella la finestra dei comandi. |
| chiaro | Rimuove le variabili dalla memoria. |
| esistere | Verifica l'esistenza di file o variabili. |
| globale | Dichiara le variabili come globali. |
| Aiuto | Cerca un argomento della guida. |
| cercare | Cerca una parola chiave nelle voci della guida. |
| smettere | Ferma MATLAB. |
| chi | Elenca le variabili correnti. |
| chi | Elenca le variabili correnti (visualizzazione lunga). |
Comandi per lavorare con il sistema
MATLAB fornisce vari comandi utili per lavorare con il sistema, come salvare il lavoro corrente nell'area di lavoro come file e caricare il file in un secondo momento.
Fornisce anche vari comandi per altre attività relative al sistema come la visualizzazione della data, l'elenco dei file nella directory, la visualizzazione della directory corrente, ecc.
La tabella seguente mostra alcuni comandi relativi al sistema di uso comune:
| Comando | Scopo |
|---|---|
| CD | Cambia la directory corrente. |
| Data | Visualizza la data corrente. |
| Elimina | Elimina un file. |
| diario | Attiva / disattiva la registrazione del file del diario. |
| dir | Elenca tutti i file nella directory corrente. |
| caricare | Carica le variabili dell'area di lavoro da un file. |
| sentiero | Visualizza il percorso di ricerca. |
| pwd | Visualizza la directory corrente. |
| Salva | Salva le variabili dell'area di lavoro in un file. |
| genere | Visualizza il contenuto di un file. |
| che cosa | Elenca tutti i file MATLAB nella directory corrente. |
| wklread | Legge il file del foglio di calcolo .wk1. |
Comandi di input e output
MATLAB fornisce i seguenti comandi relativi a input e output:
| Comando | Scopo |
|---|---|
| disp | Visualizza il contenuto di un array o di una stringa. |
| fscanf | Leggi i dati formattati da un file. |
| formato | Controlla il formato di visualizzazione dello schermo. |
| fprintf | Esegue scritture formattate su schermo o file. |
| ingresso | Visualizza i prompt e attende l'input. |
| ; | Elimina la serigrafia. |
Il fscanf e fprintfi comandi si comportano come le funzioni C scanf e printf. Supportano i seguenti codici di formato:
| Codice di formato | Scopo |
|---|---|
| %s | Formato come stringa. |
| %d | Formato come numero intero. |
| %f | Formatta come valore in virgola mobile. |
| %e | Formato come valore in virgola mobile in notazione scientifica. |
| %g | Formato nella forma più compatta:% fo% e. |
| \n | Inserisce una nuova riga nella stringa di output. |
| \t | Inserisce una tabulazione nella stringa di output. |
La funzione di formattazione ha le seguenti forme utilizzate per la visualizzazione numerica:
| Funzione di formattazione | Visualizza fino a |
|---|---|
| formato breve | Quattro cifre decimali (impostazione predefinita). |
| formato lungo | 16 cifre decimali. |
| formato breve e | Cinque cifre più esponente. |
| formato lungo e | 16 cifre più esponenti. |
| formato banca | Due cifre decimali. |
| formato + | Positivo, negativo o zero. |
| formato ratto | Approssimazione razionale. |
| formato compatto | Sopprime alcuni avanzamenti di riga. |
| formato sciolto | Ripristina la modalità di visualizzazione meno compatta. |
Comandi Vector, Matrix e Array
La tabella seguente mostra i vari comandi utilizzati per lavorare con array, matrici e vettori:
| Comando | Scopo |
|---|---|
| gatto | Concatena gli array. |
| trova | Trova indici di elementi diversi da zero. |
| lunghezza | Calcola il numero di elementi. |
| linspace | Crea un vettore spaziato regolarmente. |
| logspace | Crea un vettore spaziato logaritmicamente. |
| max | Restituisce l'elemento più grande. |
| min | Restituisce l'elemento più piccolo. |
| prod | Prodotto di ogni colonna. |
| rimodellare | Modifica le dimensioni. |
| taglia | Calcola la dimensione dell'array. |
| ordinare | Ordina ogni colonna. |
| somma | Somma ogni colonna. |
| occhio | Crea una matrice di identità. |
| ones | Creates an array of ones. |
| zeros | Creates an array of zeros. |
| cross | Computes matrix cross products. |
| dot | Computes matrix dot products. |
| det | Computes determinant of an array. |
| inv | Computes inverse of a matrix. |
| pinv | Computes pseudoinverse of a matrix. |
| rank | Computes rank of a matrix. |
| rref | Computes reduced row echelon form. |
| cell | Creates cell array. |
| celldisp | Displays cell array. |
| cellplot | Displays graphical representation of cell array. |
| num2cell | Converts numeric array to cell array. |
| deal | Matches input and output lists. |
| iscell | Identifies cell array. |
Plotting Commands
MATLAB provides numerous commands for plotting graphs. The following table shows some of the commonly used commands for plotting −
| Command | Purpose |
|---|---|
| axis | Sets axis limits. |
| fplot | Intelligent plotting of functions. |
| grid | Displays gridlines. |
| plot | Generates xy plot. |
| Prints plot or saves plot to a file. | |
| title | Puts text at top of plot. |
| xlabel | Adds text label to x-axis. |
| ylabel | Adds text label to y-axis. |
| axes | Creates axes objects. |
| close | Closes the current plot. |
| close all | Closes all plots. |
| figure | Opens a new figure window. |
| gtext | Enables label placement by mouse. |
| hold | Freezes current plot. |
| legend | Legend placement by mouse. |
| refresh | Redraws current figure window. |
| set | Specifies properties of objects such as axes. |
| subplot | Creates plots in subwindows. |
| text | Places string in figure. |
| bar | Creates bar chart. |
| loglog | Creates log-log plot. |
| polar | Creates polar plot. |
| semilogx | Creates semilog plot. (logarithmic abscissa). |
| semilogy | Creates semilog plot. (logarithmic ordinate). |
| stairs | Creates stairs plot. |
| stem | Creates stem plot. |
So far, we have used MATLAB environment as a calculator. However, MATLAB is also a powerful programming language, as well as an interactive computational environment.
In previous chapters, you have learned how to enter commands from the MATLAB command prompt. MATLAB also allows you to write series of commands into a file and execute the file as complete unit, like writing a function and calling it.
The M Files
MATLAB allows writing two kinds of program files −
Scripts − script files are program files with .m extension. In these files, you write series of commands, which you want to execute together. Scripts do not accept inputs and do not return any outputs. They operate on data in the workspace.
Functions − functions files are also program files with .m extension. Functions can accept inputs and return outputs. Internal variables are local to the function.
You can use the MATLAB editor or any other text editor to create your .mfiles. In this section, we will discuss the script files. A script file contains multiple sequential lines of MATLAB commands and function calls. You can run a script by typing its name at the command line.
Creating and Running Script File
To create scripts files, you need to use a text editor. You can open the MATLAB editor in two ways −
- Using the command prompt
- Using the IDE
If you are using the command prompt, type edit in the command prompt. This will open the editor. You can directly type edit and then the filename (with .m extension)
edit
Or
edit <filename>The above command will create the file in default MATLAB directory. If you want to store all program files in a specific folder, then you will have to provide the entire path.
Let us create a folder named progs. Type the following commands at the command prompt (>>) −
mkdir progs % create directory progs under default directory
chdir progs % changing the current directory to progs
edit prog1.m % creating an m file named prog1.mIf you are creating the file for first time, MATLAB prompts you to confirm it. Click Yes.
Alternatively, if you are using the IDE, choose NEW -> Script. This also opens the editor and creates a file named Untitled. You can name and save the file after typing the code.
Type the following code in the editor −
NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
+ NonTeachingStaff;
disp(Total);After creating and saving the file, you can run it in two ways −
Clicking the Run button on the editor window or
Just typing the filename (without extension) in the command prompt: >> prog1
The command window prompt displays the result −
6170Example
Create a script file, and type the following code −
a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)When the above code is compiled and executed, it produces the following result −
c = 12
d = 12.657
e = 63.285
f = 3.1852e-06MATLAB does not require any type declaration or dimension statements. Whenever MATLAB encounters a new variable name, it creates the variable and allocates appropriate memory space.
If the variable already exists, then MATLAB replaces the original content with new content and allocates new storage space, where necessary.
For example,
Total = 42The above statement creates a 1-by-1 matrix named 'Total' and stores the value 42 in it.
Data Types Available in MATLAB
MATLAB provides 15 fundamental data types. Every data type stores data that is in the form of a matrix or array. The size of this matrix or array is a minimum of 0-by-0 and this can grow up to a matrix or array of any size.
The following table shows the most commonly used data types in MATLAB −
| Sr.No. | Data Type & Description |
|---|---|
| 1 | int8 8-bit signed integer |
| 2 | uint8 8-bit unsigned integer |
| 3 | int16 16-bit signed integer |
| 4 | uint16 16-bit unsigned integer |
| 5 | int32 32-bit signed integer |
| 6 | uint32 32-bit unsigned integer |
| 7 | int64 64-bit signed integer |
| 8 | uint64 64-bit unsigned integer |
| 9 | single single precision numerical data |
| 10 | double double precision numerical data |
| 11 | logical logical values of 1 or 0, represent true and false respectively |
| 12 | char character data (strings are stored as vector of characters) |
| 13 | cell array array of indexed cells, each capable of storing an array of a different dimension and data type |
| 14 | structure C-like structures, each structure having named fields capable of storing an array of a different dimension and data type |
| 15 | function handle pointer to a function |
| 16 | user classes objects constructed from a user-defined class |
| 17 | java classes objects constructed from a Java class |
Example
Create a script file with the following code −
str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)When the above code is compiled and executed, it produces the following result −
str = Hello World!
n = 2345
d = 2345
un = 790
rn = 5678.9
c = 5679Data Type Conversion
MATLAB provides various functions for converting, a value from one data type to another. The following table shows the data type conversion functions −
| Function | Purpose |
|---|---|
| char | Convert to character array (string) |
| int2str | Convert integer data to string |
| mat2str | Convert matrix to string |
| num2str | Convert number to string |
| str2double | Convert string to double-precision value |
| str2num | Convert string to number |
| native2unicode | Convert numeric bytes to Unicode characters |
| unicode2native | Convert Unicode characters to numeric bytes |
| base2dec | Convert base N number string to decimal number |
| bin2dec | Convert binary number string to decimal number |
| dec2base | Convert decimal to base N number in string |
| dec2bin | Convert decimal to binary number in string |
| dec2hex | Convert decimal to hexadecimal number in string |
| hex2dec | Convert hexadecimal number string to decimal number |
| hex2num | Convert hexadecimal number string to double-precision number |
| num2hex | Convert singles and doubles to IEEE hexadecimal strings |
| cell2mat | Convert cell array to numeric array |
| cell2struct | Convert cell array to structure array |
| cellstr | Create cell array of strings from character array |
| mat2cell | Convert array to cell array with potentially different sized cells |
| num2cell | Convert array to cell array with consistently sized cells |
| struct2cell | Convert structure to cell array |
Determination of Data Types
MATLAB provides various functions for identifying data type of a variable.
Following table provides the functions for determining the data type of a variable −
| Function | Purpose |
|---|---|
| is | Detect state |
| isa | Determine if input is object of specified class |
| iscell | Determine whether input is cell array |
| iscellstr | Determine whether input is cell array of strings |
| ischar | Determine whether item is character array |
| isfield | Determine whether input is structure array field |
| isfloat | Determine if input is floating-point array |
| ishghandle | True for Handle Graphics object handles |
| isinteger | Determine if input is integer array |
| isjava | Determine if input is Java object |
| islogical | Determine if input is logical array |
| isnumeric | Determine if input is numeric array |
| isobject | Determine if input is MATLAB object |
| isreal | Check if input is real array |
| isscalar | Determine whether input is scalar |
| isstr | Determine whether input is character array |
| isstruct | Determine whether input is structure array |
| isvector | Determine whether input is vector |
| class | Determine class of object |
| validateattributes | Check validity of array |
| whos | List variables in workspace, with sizes and types |
Example
Create a script file with the following code −
x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)When you run the file, it produces the following result −
x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =
1 2 3
ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations. MATLAB is designed to operate primarily on whole matrices and arrays. Therefore, operators in MATLAB work both on scalar and non-scalar data. MATLAB allows the following types of elementary operations −
- Arithmetic Operators
- Relational Operators
- Logical Operators
- Bitwise Operations
- Set Operations
Arithmetic Operators
MATLAB allows two different types of arithmetic operations −
- Matrix arithmetic operations
- Array arithmetic operations
Matrix arithmetic operations are same as defined in linear algebra. Array operations are executed element by element, both on one-dimensional and multidimensional array.
The matrix operators and array operators are differentiated by the period (.) symbol. However, as the addition and subtraction operation is same for matrices and arrays, the operator is same for both cases. The following table gives brief description of the operators −
Show Examples
| Sr.No. | Operator & Description |
|---|---|
| 1 | + Addition or unary plus. A+B adds the values stored in variables A and B. A and B must have the same size, unless one is a scalar. A scalar can be added to a matrix of any size. |
| 2 | - Subtraction or unary minus. A-B subtracts the value of B from A. A and B must have the same size, unless one is a scalar. A scalar can be subtracted from a matrix of any size. |
| 3 | * Matrix multiplication. C = A*B is the linear algebraic product of the matrices A and B. More precisely,
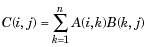
For non-scalar A and B, the number of columns of A must be equal to the number of rows of B. A scalar can multiply a matrix of any size. |
| 4 | .* Array multiplication. A.*B is the element-by-element product of the arrays A and B. A and B must have the same size, unless one of them is a scalar. |
| 5 | / Slash or matrix right division. B/A is roughly the same as B*inv(A). More precisely, B/A = (A'\B')'. |
| 6 | ./ Array right division. A./B is the matrix with elements A(i,j)/B(i,j). A and B must have the same size, unless one of them is a scalar. |
| 7 | \ Backslash or matrix left division. If A is a square matrix, A\B is roughly the same as inv(A)*B, except it is computed in a different way. If A is an n-by-n matrix and B is a column vector with n components, or a matrix with several such columns, then X = A\B is the solution to the equation AX = B. A warning message is displayed if A is badly scaled or nearly singular. |
| 8 | .\ Array left division. A.\B is the matrix with elements B(i,j)/A(i,j). A and B must have the same size, unless one of them is a scalar. |
| 9 | ^ Matrix power. X^p is X to the power p, if p is a scalar. If p is an integer, the power is computed by repeated squaring. If the integer is negative, X is inverted first. For other values of p, the calculation involves eigenvalues and eigenvectors, such that if [V,D] = eig(X), then X^p = V*D.^p/V. |
| 10 | .^ Array power. A.^B is the matrix with elements A(i,j) to the B(i,j) power. A and B must have the same size, unless one of them is a scalar. |
| 11 | ' Matrix transpose. A' is the linear algebraic transpose of A. For complex matrices, this is the complex conjugate transpose. |
| 12 | .' Array transpose. A.' is the array transpose of A. For complex matrices, this does not involve conjugation. |
Relational Operators
Relational operators can also work on both scalar and non-scalar data. Relational operators for arrays perform element-by-element comparisons between two arrays and return a logical array of the same size, with elements set to logical 1 (true) where the relation is true and elements set to logical 0 (false) where it is not.
The following table shows the relational operators available in MATLAB −
Show Examples
| Sr.No. | Operator & Description |
|---|---|
| 1 | < Less than |
| 2 | <= Less than or equal to |
| 3 | > Greater than |
| 4 | >= Greater than or equal to |
| 5 | == Equal to |
| 6 | ~= Not equal to |
Logical Operators
MATLAB offers two types of logical operators and functions −
Element-wise − These operators operate on corresponding elements of logical arrays.
Short-circuit − These operators operate on scalar and, logical expressions.
Element-wise logical operators operate element-by-element on logical arrays. The symbols &, |, and ~ are the logical array operators AND, OR, and NOT.
Short-circuit logical operators allow short-circuiting on logical operations. The symbols && and || are the logical short-circuit operators AND and OR.
Show Examples
Bitwise Operations
Bitwise operators work on bits and perform bit-by-bit operation. The truth tables for &, |, and ^ are as follows −
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Assume if A = 60; and B = 13; Now in binary format they will be as follows −
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A = 1100 0011
MATLAB provides various functions for bit-wise operations like 'bitwise and', 'bitwise or' and 'bitwise not' operations, shift operation, etc.
The following table shows the commonly used bitwise operations −
Show Examples
| Function | Purpose |
|---|---|
| bitand(a, b) | Bit-wise AND of integers a and b |
| bitcmp(a) | Bit-wise complement of a |
| bitget(a,pos) | Get bit at specified position pos, in the integer array a |
| bitor(a, b) | Bit-wise OR of integers a and b |
| bitset(a, pos) | Set bit at specific location pos of a |
| bitshift(a, k) | Returns a shifted to the left by k bits, equivalent to multiplying by 2k. Negative values of k correspond to shifting bits right or dividing by 2|k| and rounding to the nearest integer towards negative infinite. Any overflow bits are truncated. |
| bitxor(a, b) | Bit-wise XOR of integers a and b |
| swapbytes | Swap byte ordering |
Set Operations
MATLAB provides various functions for set operations, like union, intersection and testing for set membership, etc.
The following table shows some commonly used set operations −
Show Examples
| Sr.No. | Function & Description |
|---|---|
| 1 | intersect(A,B) Set intersection of two arrays; returns the values common to both A and B. The values returned are in sorted order. |
| 2 | intersect(A,B,'rows') Treats each row of A and each row of B as single entities and returns the rows common to both A and B. The rows of the returned matrix are in sorted order. |
| 3 | ismember(A,B) Returns an array the same size as A, containing 1 (true) where the elements of A are found in B. Elsewhere, it returns 0 (false). |
| 4 | ismember(A,B,'rows') Treats each row of A and each row of B as single entities and returns a vector containing 1 (true) where the rows of matrix A are also rows of B. Elsewhere, it returns 0 (false). |
| 5 | issorted(A) Returns logical 1 (true) if the elements of A are in sorted order and logical 0 (false) otherwise. Input A can be a vector or an N-by-1 or 1-by-N cell array of strings. A is considered to be sorted if A and the output of sort(A) are equal. |
| 6 | issorted(A, 'rows') Returns logical 1 (true) if the rows of two-dimensional matrix A is in sorted order, and logical 0 (false) otherwise. Matrix A is considered to be sorted if A and the output of sortrows(A) are equal. |
| 7 | setdiff(A,B) Sets difference of two arrays; returns the values in A that are not in B. The values in the returned array are in sorted order. |
| 8 | setdiff(A,B,'rows') Treats each row of A and each row of B as single entities and returns the rows from A that are not in B. The rows of the returned matrix are in sorted order. The 'rows' option does not support cell arrays. |
| 9 | setxor Sets exclusive OR of two arrays |
| 10 | union Sets union of two arrays |
| 11 | unique Unique values in array |
Decision making structures require that the programmer should specify one or more conditions to be evaluated or tested by the program, along with a statement or statements to be executed if the condition is determined to be true, and optionally, other statements to be executed if the condition is determined to be false.
Following is the general form of a typical decision making structure found in most of the programming languages −
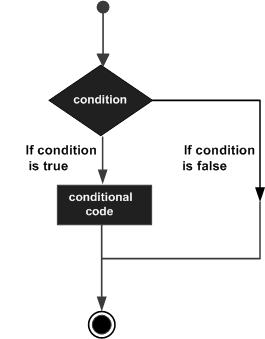
MATLAB provides following types of decision making statements. Click the following links to check their detail −
| Sr.No. | Statement & Description |
|---|---|
| 1 | if ... end statement An if ... end statement consists of a boolean expression followed by one or more statements. |
| 2 | if...else...end statement An if statement can be followed by an optional else statement, which executes when the boolean expression is false. |
| 3 | If... elseif...elseif...else...end statements An if statement can be followed by one (or more) optional elseif... and an else statement, which is very useful to test various conditions. |
| 4 | nested if statements You can use one if or elseif statement inside another if or elseif statement(s). |
| 5 | switch statement A switch statement allows a variable to be tested for equality against a list of values. |
| 6 | nested switch statements You can use one switch statement inside another switch statement(s). |
There may be a situation when you need to execute a block of code several number of times. In general, statements are executed sequentially. The first statement in a function is executed first, followed by the second, and so on.
Programming languages provide various control structures that allow for more complicated execution paths.
A loop statement allows us to execute a statement or group of statements multiple times and following is the general form of a loop statement in most of the programming languages −
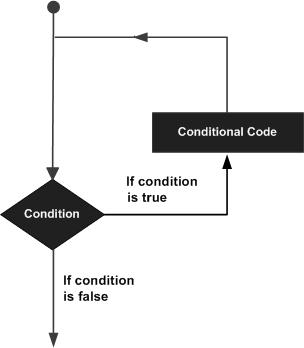
MATLAB provides following types of loops to handle looping requirements. Click the following links to check their detail −
| Sr.No. | Loop Type & Description |
|---|---|
| 1 | while loop Repeats a statement or group of statements while a given condition is true. It tests the condition before executing the loop body. |
| 2 | for loop Executes a sequence of statements multiple times and abbreviates the code that manages the loop variable. |
| 3 | nested loops You can use one or more loops inside any another loop. |
Loop Control Statements
Loop control statements change execution from its normal sequence. When execution leaves a scope, all automatic objects that were created in that scope are destroyed.
MATLAB supports the following control statements. Click the following links to check their detail.
| Sr.No. | Control Statement & Description |
|---|---|
| 1 | break statement Terminates the loop statement and transfers execution to the statement immediately following the loop. |
| 2 | continue statement Causes the loop to skip the remainder of its body and immediately retest its condition prior to reiterating. |
A vector is a one-dimensional array of numbers. MATLAB allows creating two types of vectors −
- Row vectors
- Column vectors
Row Vectors
Row vectors are created by enclosing the set of elements in square brackets, using space or comma to delimit the elements.
r = [7 8 9 10 11]MATLAB will execute the above statement and return the following result −
r =
7 8 9 10 11Column Vectors
Column vectors are created by enclosing the set of elements in square brackets, using semicolon to delimit the elements.
c = [7; 8; 9; 10; 11]MATLAB will execute the above statement and return the following result −
c =
7
8
9
10
11Referencing the Elements of a Vector
You can reference one or more of the elements of a vector in several ways. The ith component of a vector v is referred as v(i). For example −
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(3)MATLAB will execute the above statement and return the following result −
ans = 3When you reference a vector with a colon, such as v(:), all the components of the vector are listed.
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(:)MATLAB will execute the above statement and return the following result −
ans =
1
2
3
4
5
6MATLAB allows you to select a range of elements from a vector.
For example, let us create a row vector rv of 9 elements, then we will reference the elements 3 to 7 by writing rv(3:7) and create a new vector named sub_rv.
rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)MATLAB will execute the above statement and return the following result −
sub_rv =
3 4 5 6 7Vector Operations
In this section, let us discuss the following vector operations −
Addition and Subtraction of Vectors
Scalar Multiplication of Vectors
Transpose of a Vector
Appending Vectors
Magnitude of a Vector
Vector Dot Product
Vectors with Uniformly Spaced Elements
A matrix is a two-dimensional array of numbers.
In MATLAB, you create a matrix by entering elements in each row as comma or space delimited numbers and using semicolons to mark the end of each row.
For example, let us create a 4-by-5 matrix a −
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]MATLAB will execute the above statement and return the following result −
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8Referencing the Elements of a Matrix
To reference an element in the mth row and nth column, of a matrix mx, we write −
mx(m, n);Ad esempio, per riferirsi all'elemento nella 2 ° riga e 5 ° colonna della matrice una , come creato nella sezione precedente, digitiamo -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 6Per fare riferimento a tutti gli elementi nella m esima colonna digitiamo A (:, m).
Creiamo un vettore colonna v, dagli elementi della quarta riga della matrice a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
v =
4
5
6
7Puoi anche selezionare gli elementi dalla m esima alla ennesima colonna, per questo scriviamo:
a(:,m:n)Creiamo una matrice più piccola prendendo gli elementi dalla seconda e dalla terza colonna -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
2 3
3 4
4 5
5 6Allo stesso modo, puoi creare una sotto-matrice prendendo una sotto-parte di una matrice.
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
2 3
3 4
4 5
5 6Allo stesso modo, puoi creare una sotto-matrice prendendo una sotto-parte di una matrice.
Ad esempio, creiamo una sotto-matrice sa prendendo la sottoparte interna di a -
3 4 5
4 5 6Per fare questo, scrivi:
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
sa =
3 4 5
4 5 6Eliminazione di una riga o di una colonna in una matrice
È possibile eliminare un'intera riga o colonna di una matrice assegnando un insieme vuoto di parentesi quadre [] a quella riga o colonna. Fondamentalmente, [] denota un array vuoto.
Ad esempio, eliminiamo la quarta riga di un -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7Quindi, eliminiamo la quinta colonna di a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
a =
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7Esempio
In questo esempio, creiamo una matrice 3 per 3 m, quindi copieremo la seconda e la terza riga di questa matrice due volte per creare una matrice 4 per 3.
Crea un file di script con il codice seguente:
a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)Quando si esegue il file, viene visualizzato il seguente risultato:
new_mat =
4 5 6
7 8 9
4 5 6
7 8 9Operazioni con matrici
In questa sezione, discutiamo le seguenti operazioni con le matrici di base e comunemente usate:
Addizione e sottrazione di matrici
Divisione delle matrici
Operazioni scalari delle matrici
Trasposizione di una matrice
Matrici concatenate
Moltiplicazione di matrici
Determinante di una matrice
Inverso di una matrice
Tutte le variabili di tutti i tipi di dati in MATLAB sono array multidimensionali. Un vettore è un array unidimensionale e una matrice è un array bidimensionale.
Abbiamo già discusso di vettori e matrici. In questo capitolo, discuteremo di array multidimensionali. Tuttavia, prima di ciò, esaminiamo alcuni tipi speciali di array.
Array speciali in MATLAB
In questa sezione, discuteremo alcune funzioni che creano alcuni array speciali. Per tutte queste funzioni, un singolo argomento crea un array quadrato, i doppi argomenti creano un array rettangolare.
Il zeros() la funzione crea un array di tutti zeri -
Ad esempio:
zeros(5)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0Il ones() la funzione crea un array di tutti quelli -
Ad esempio:
ones(4,3)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
1 1 1
1 1 1
1 1 1
1 1 1Il eye() la funzione crea una matrice di identità.
Ad esempio:
eye(4)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1Il rand() la funzione crea un array di numeri casuali distribuiti uniformemente su (0,1) -
Ad esempio:
rand(3, 5)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
0.8147 0.9134 0.2785 0.9649 0.9572
0.9058 0.6324 0.5469 0.1576 0.4854
0.1270 0.0975 0.9575 0.9706 0.8003Un quadrato magico
UN magic square è un quadrato che produce la stessa somma, quando i suoi elementi vengono aggiunti per riga, per colonna o diagonalmente.
Il magic()la funzione crea una matrice quadrata magica. Ci vuole un argomento singolare che dia la dimensione del quadrato. L'argomento deve essere uno scalare maggiore o uguale a 3.
magic(4)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1Array multidimensionali
Un array con più di due dimensioni è chiamato array multidimensionale in MATLAB. Gli array multidimensionali in MATLAB sono un'estensione della normale matrice bidimensionale.
Generalmente per generare un array multidimensionale, creiamo prima un array bidimensionale e lo estendiamo.
Ad esempio, creiamo un array bidimensionale a.
a = [7 9 5; 6 1 9; 4 3 2]MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
a =
7 9 5
6 1 9
4 3 2L'array a è un array 3 per 3; possiamo aggiungere una terza dimensione a a , fornendo valori come -
a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
a =
ans(:,:,1) =
0 0 0
0 0 0
0 0 0
ans(:,:,2) =
1 2 3
4 5 6
7 8 9Possiamo anche creare array multidimensionali usando le funzioni ones (), zeros () o rand ().
Per esempio,
b = rand(4,3,2)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
b(:,:,1) =
0.0344 0.7952 0.6463
0.4387 0.1869 0.7094
0.3816 0.4898 0.7547
0.7655 0.4456 0.2760
b(:,:,2) =
0.6797 0.4984 0.2238
0.6551 0.9597 0.7513
0.1626 0.3404 0.2551
0.1190 0.5853 0.5060Possiamo anche usare il cat()funzione per costruire array multidimensionali. Concatena un elenco di array lungo una dimensione specificata -
La sintassi per la funzione cat () è -
B = cat(dim, A1, A2...)Dove,
B è il nuovo array creato
A1 , A2 , ... sono gli array da concatenare
dim è la dimensione lungo la quale concatenare gli array
Esempio
Crea un file di script e digita il seguente codice al suo interno:
a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])Quando esegui il file, viene visualizzato:
c(:,:,1) =
9 8 7
6 5 4
3 2 1
c(:,:,2) =
1 2 3
4 5 6
7 8 9
c(:,:,3) =
2 3 1
4 7 8
3 9 0Funzioni array
MATLAB fornisce le seguenti funzioni per ordinare, ruotare, permutare, rimodellare o spostare i contenuti dell'array.
| Funzione | Scopo |
|---|---|
| lunghezza | Lunghezza del vettore o dimensione massima della matrice |
| ndims | Numero di dimensioni della matrice |
| numel | Numero di elementi dell'array |
| taglia | Dimensioni della matrice |
| iscolumn | Determina se l'input è un vettore colonna |
| è vuoto | Determina se l'array è vuoto |
| ismatrix | Determina se l'input è una matrice |
| isrow | Determina se l'input è un vettore riga |
| isscalar | Determina se l'input è scalare |
| isvector | Determina se l'input è vettoriale |
| blkdiag | Costruisce la matrice diagonale a blocchi dagli argomenti di input |
| circshift | Sposta l'array in modo circolare |
| ctranspose | Trasposizione coniugata complessa |
| diag | Matrici diagonali e diagonali di matrice |
| flipdim | Capovolge la matrice lungo la dimensione specificata |
| fliplr | Capovolge la matrice da sinistra a destra |
| flipud | Capovolge la matrice dall'alto verso il basso |
| ipermuto | Le inversioni permutano le dimensioni della matrice ND |
| permutare | Riorganizza le dimensioni della matrice ND |
| repmat | Repliche e array di piastrelle |
| rimodellare | Rimodella l'array |
| rot90 | Ruota la matrice di 90 gradi |
| shiftdim | Cambia le dimensioni |
| smistato | Determina se gli elementi dell'insieme sono in ordine ordinato |
| ordinare | Ordina gli elementi dell'array in ordine crescente o decrescente |
| sortrows | Ordina le righe in ordine crescente |
| spremere | Rimuove le dimensioni singleton |
| trasporre | Trasporre |
| vettorializzare | Vettorizza l'espressione |
Esempi
I seguenti esempi illustrano alcune delle funzioni sopra menzionate.
Length, Dimension and Number of elements −
Crea un file di script e digita il seguente codice al suo interno:
x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x) % length of x vector
y = rand(3, 4, 5, 2);
ndims(y) % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s) % no of elements in sQuando si esegue il file, viene visualizzato il seguente risultato:
ans = 8
ans = 4
ans = 23Circular Shifting of the Array Elements −
Crea un file di script e digita il seguente codice al suo interno:
a = [1 2 3; 4 5 6; 7 8 9] % the original array a
b = circshift(a,1) % circular shift first dimension values down by 1.
c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1
% and second dimension values to the left % by 1.Quando si esegue il file, viene visualizzato il seguente risultato:
a =
1 2 3
4 5 6
7 8 9
b =
7 8 9
1 2 3
4 5 6
c =
8 9 7
2 3 1
5 6 4Ordinamento di array
Crea un file di script e digita il seguente codice al suo interno:
v = [ 23 45 12 9 5 0 19 17] % horizontal vector
sort(v) % sorting v
m = [2 6 4; 5 3 9; 2 0 1] % two dimensional array
sort(m, 1) % sorting m along the row
sort(m, 2) % sorting m along the columnQuando si esegue il file, viene visualizzato il seguente risultato:
v =
23 45 12 9 5 0 19 17
ans =
0 5 9 12 17 19 23 45
m =
2 6 4
5 3 9
2 0 1
ans =
2 0 1
2 3 4
5 6 9
ans =
2 4 6
3 5 9
0 1 2Cell Array
Gli array di celle sono array di celle indicizzate in cui ogni cella può memorizzare un array di dimensioni e tipi di dati diversi.
Il cellviene utilizzata per creare un array di celle. La sintassi per la funzione cella è -
C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)Dove,
C è l'array di celle;
dim è un numero intero scalare o un vettore di numeri interi che specifica le dimensioni della matrice di celle C;
dim1, ..., dimN sono numeri interi scalari che specificano le dimensioni di C;
obj è uno dei seguenti:
- Matrice o oggetto Java
- Matrice .NET di tipo System.String o System.Object
Esempio
Crea un file di script e digita il seguente codice al suo interno:
c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}Quando si esegue il file, viene visualizzato il seguente risultato:
c =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
[1,3] = Green
[2,3] = 3
[1,4] = Yellow
[2,4] = 4
[1,5] = White
[2,5] = 5
}Accesso ai dati negli array di celle
Esistono due modi per fare riferimento agli elementi di un array di celle:
- Racchiudere gli indici nella prima parentesi (), per fare riferimento a gruppi di celle
- Racchiudere gli indici tra parentesi graffe {}, per fare riferimento ai dati all'interno delle singole celle
Quando racchiudi gli indici nella prima parentesi, si riferisce al gruppo di celle.
Gli indici degli array di celle tra parentesi morbide si riferiscono a gruppi di celle.
Ad esempio:
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
}È inoltre possibile accedere ai contenuti delle celle indicizzandoli con parentesi graffe.
Ad esempio:
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = Blue
ans = Green
ans = YellowIl colon(:)è uno degli operatori più utili in MATLAB. Viene utilizzato per creare vettori, array di pedici especify for iterations.
Se vuoi creare un vettore riga, contenente numeri interi da 1 a 10, scrivi -
1:10MATLAB esegue l'istruzione e restituisce un vettore riga contenente gli interi da 1 a 10 -
ans =
1 2 3 4 5 6 7 8 9 10Se si desidera specificare un valore di incremento diverso da uno, ad esempio:
100: -5: 50MATLAB esegue l'istruzione e restituisce il seguente risultato:
ans =
100 95 90 85 80 75 70 65 60 55 50Facciamo un altro esempio:
0:pi/8:piMATLAB esegue l'istruzione e restituisce il seguente risultato:
ans =
Columns 1 through 7
0 0.3927 0.7854 1.1781 1.5708 1.9635 2.3562
Columns 8 through 9
2.7489 3.1416È possibile utilizzare l'operatore dei due punti per creare un vettore di indici per selezionare righe, colonne o elementi di array.
La tabella seguente descrive il suo utilizzo per questo scopo (si dia una matrice A) -
| Formato | Scopo |
|---|---|
| A(:,j) | è la jesima colonna di A. |
| A(i,:) | è l'ennesima riga di A. |
| A(:,:) | è la matrice bidimensionale equivalente. Per le matrici è lo stesso di A. |
| A(j:k) | è A (j), A (j + 1), ..., A (k). |
| A(:,j:k) | è A (:, j), A (:, j + 1), ..., A (:, k). |
| A(:,:,k) | è la k- esima pagina dell'array tridimensionale A. |
| A(i,j,k,:) | è un vettore nella matrice quadridimensionale A. Il vettore include A (i, j, k, 1), A (i, j, k, 2), A (i, j, k, 3) e così via. |
| A(:) | sono tutti gli elementi di A, considerati come un'unica colonna. Sul lato sinistro di un'istruzione di assegnazione, A (:) riempie A, preservandone la forma di prima. In questo caso, il lato destro deve contenere lo stesso numero di elementi di A. |
Esempio
Crea un file di script e digita il seguente codice al suo interno:
A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2) % second column of A
A(:,2:3) % second and third column of A
A(2:3,2:3) % second and third rows and second and third columnsQuando si esegue il file, viene visualizzato il seguente risultato:
A =
1 2 3 4
4 5 6 7
7 8 9 10
ans =
2
5
8
ans =
2 3
5 6
8 9
ans =
5 6
8 9MATLAB supporta varie classi numeriche che includono interi con e senza segno e numeri in virgola mobile a precisione singola e doppia. Per impostazione predefinita, MATLAB memorizza tutti i valori numerici come numeri in virgola mobile a precisione doppia.
È possibile scegliere di memorizzare qualsiasi numero o matrice di numeri come numeri interi o come numeri a precisione singola.
Tutti i tipi numerici supportano le operazioni di base degli array e le operazioni matematiche.
Conversione in vari tipi di dati numerici
MATLAB fornisce le seguenti funzioni per convertire in vari tipi di dati numerici:
| Funzione | Scopo |
|---|---|
| Doppio | Converte in un numero a doppia precisione |
| single | Converte in un numero a precisione singola |
| int8 | Converte in un intero con segno a 8 bit |
| int16 | Converte in un intero con segno a 16 bit |
| int32 | Converte in un intero con segno a 32 bit |
| int64 | Converte in un intero con segno a 64 bit |
| uint8 | Converte in un intero senza segno a 8 bit |
| uint16 | Converte in un intero senza segno a 16 bit |
| uint32 | Converte in un intero senza segno a 32 bit |
| uint64 | Converte in un intero senza segno a 64 bit |
Esempio
Crea un file di script e digita il codice seguente:
x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5Quando esegui il file, mostra il seguente risultato:
x =
39.900 26.025 47.100
x =
39.900 26.025 47.100
x =
38 23 45
x =
38 23 45
x =
38 23 45
x =
38 23 45Esempio
Estendiamo ancora un po 'l'esempio precedente. Crea un file di script e digita il codice seguente:
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)Quando esegui il file, mostra il seguente risultato:
x =
38 23 45
x =
38 23 45
x =
{
[1,1] = 38
[1,2] = 23
[1,3] = 45
}Numeri interi più piccoli e più grandi
Le funzioni intmax() e intmin() restituisce i valori massimo e minimo che possono essere rappresentati con tutti i tipi di numeri interi.
Entrambe le funzioni accettano il tipo di dati intero come argomento, ad esempio, intmax (int8) o intmin (int64) e restituiscono i valori massimo e minimo che è possibile rappresentare con il tipo di dati intero.
Esempio
Il seguente esempio illustra come ottenere i valori più piccoli e più grandi di interi. Crea un file di script e scrivi il seguente codice al suo interno:
% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))Quando esegui il file, mostra il seguente risultato:
ans = The range for int8 is:
-128 to 127
ans = The range for int16 is:
-32768 to 32767
ans = The range for int32 is:
-2147483648 to 2147483647
ans = The range for int64 is:
0 to 0
ans = The range for uint8 is:
0 to 255
ans = The range for uint16 is:
0 to 65535
ans = The range for uint32 is:
0 to -1
ans = The range for uint64 is:
0 to 18446744073709551616Numeri in virgola mobile più piccoli e più grandi
Le funzioni realmax() e realmin() restituisce i valori massimo e minimo che possono essere rappresentati con numeri in virgola mobile.
Entrambe le funzioni, quando chiamate con l'argomento 'single', restituiscono i valori massimo e minimo che puoi rappresentare con il tipo di dati a precisione singola e quando chiamate con l'argomento 'double', restituiscono i valori massimo e minimo che puoi rappresentare con il tipo di dati a doppia precisione.
Esempio
Il seguente esempio illustra come ottenere i numeri in virgola mobile più piccoli e più grandi. Crea un file di script e scrivi il seguente codice al suo interno:
% displaying the smallest and largest single-precision
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
realmin('single'), realmax('single'))
% displaying the smallest and largest double-precision
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
realmin('double'), realmax('double'))Quando si esegue il file, viene visualizzato il seguente risultato:
ans = The range for single is:
-3.40282e+38 to -1.17549e-38 and
1.17549e-38 to 3.40282e+38
ans = The range for double is:
-1.79769e+308 to -2.22507e-308 and
2.22507e-308 to 1.79769e+308Creare una stringa di caratteri è abbastanza semplice in MATLAB. In effetti, l'abbiamo usato molte volte. Ad esempio, digiti quanto segue nel prompt dei comandi:
my_string = 'Tutorials Point'MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
my_string = Tutorials PointMATLAB considera tutte le variabili come array e le stringhe sono considerate come array di caratteri. Usiamo il filewhos comando per controllare la variabile creata sopra -
whosMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
Name Size Bytes Class Attributes
my_string 1x16 32 charÈ interessante notare che puoi utilizzare funzioni di conversione numerica come uint8 o uint16per convertire i caratteri nella stringa nei rispettivi codici numerici. Ilchar la funzione converte il vettore intero in caratteri -
Esempio
Crea un file di script e digita il seguente codice al suo interno:
my_string = 'Tutorial''s Point';
str_ascii = uint8(my_string) % 8-bit ascii values
str_back_to_char= char(str_ascii)
str_16bit = uint16(my_string) % 16-bit ascii values
str_back_to_char = char(str_16bit)Quando si esegue il file, viene visualizzato il seguente risultato:
str_ascii =
84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116
str_back_to_char = Tutorial's Point
str_16bit =
84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116
str_back_to_char = Tutorial's PointMatrice di caratteri rettangolare
Le stringhe che abbiamo discusso finora sono array di caratteri unidimensionali; tuttavia, dobbiamo archiviare più di questo. Abbiamo bisogno di memorizzare più dati testuali dimensionali nel nostro programma. Ciò si ottiene creando matrici di caratteri rettangolari.
Il modo più semplice per creare un array di caratteri rettangolare è concatenare due o più array di caratteri unidimensionali, verticalmente o orizzontalmente secondo necessità.
Puoi combinare le stringhe verticalmente in uno dei seguenti modi:
Utilizzo dell'operatore di concatenazione MATLAB []e separando ogni riga con un punto e virgola (;). Tieni presente che in questo metodo ogni riga deve contenere lo stesso numero di caratteri. Per stringhe con lunghezze diverse, è necessario riempire con caratteri spazio secondo necessità.
Usando il charfunzione. Se le stringhe hanno lunghezze diverse, il carattere riempie le stringhe più corte con spazi finali in modo che ogni riga abbia lo stesso numero di caratteri.
Esempio
Crea un file di script e digita il seguente codice al suo interno:
doc_profile = ['Zara Ali '; ...
'Sr. Surgeon '; ...
'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
'RN Tagore Cardiology Research Center')Quando si esegue il file, viene visualizzato il seguente risultato:
doc_profile =
Zara Ali
Sr. Surgeon
R N Tagore Cardiology Research Center
doc_profile =
Zara Ali
Sr. Surgeon
RN Tagore Cardiology Research CenterPuoi combinare le stringhe orizzontalmente in uno dei seguenti modi:
Utilizzando l'operatore di concatenazione MATLAB, []e separando le stringhe di input con una virgola o uno spazio. Questo metodo preserva gli spazi finali negli array di input.
Utilizzando la funzione di concatenazione di stringhe, strcat. Questo metodo rimuove gli spazi finali negli input.
Esempio
Crea un file di script e digita il seguente codice al suo interno:
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)Quando si esegue il file, viene visualizzato il seguente risultato:
profile = Zara Ali , Sr. Surgeon , R N Tagore Cardiology Research Center
profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research CenterCombinazione di stringhe in una matrice di celle
Dalla nostra discussione precedente, è chiaro che la combinazione di stringhe con lunghezze diverse potrebbe essere un problema poiché tutte le stringhe nell'array devono essere della stessa lunghezza. Abbiamo utilizzato spazi vuoti alla fine delle stringhe per equalizzarne la lunghezza.
Tuttavia, un modo più efficiente per combinare le stringhe consiste nel convertire la matrice risultante in una matrice di celle.
L'array di celle MATLAB può contenere diverse dimensioni e tipi di dati in un array. Gli array di celle forniscono un modo più flessibile per memorizzare stringhe di lunghezza variabile.
Il cellstr funzione converte una matrice di caratteri in una matrice di celle di stringhe.
Esempio
Crea un file di script e digita il seguente codice al suo interno:
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)Quando si esegue il file, viene visualizzato il seguente risultato:
{
[1,1] = Zara Ali
[2,1] = Sr. Surgeon
[3,1] = R N Tagore Cardiology Research Center
}Funzioni di stringa in MATLAB
MATLAB fornisce numerose funzioni per stringhe che creano, combinano, analizzano, confrontano e manipolano stringhe.
La tabella seguente fornisce una breve descrizione delle funzioni stringa in MATLAB -
| Funzione | Scopo |
|---|---|
| Funzioni per memorizzare testo in matrici di caratteri, combinare matrici di caratteri, ecc. | |
| spazi vuoti | Crea una stringa di caratteri vuoti |
| cellstr | Crea una matrice di celle di stringhe dalla matrice di caratteri |
| char | Converti in matrice di caratteri (stringa) |
| iscellstr | Determina se l'input è un array di celle di stringhe |
| ischar | Determina se l'elemento è un array di caratteri |
| sprintf | Formatta i dati in una stringa |
| strcat | Concatena le stringhe orizzontalmente |
| strjoin | Unisci le stringhe nella matrice di celle in una singola stringa |
| Funzioni per identificare parti di stringhe, trovare e sostituire sottostringhe | |
| ischar | Determina se l'elemento è un array di caratteri |
| isletter | Elementi della matrice che sono lettere alfabetiche |
| isspace | Elementi di matrice che sono caratteri spaziali |
| isstrprop | Determina se la stringa appartiene alla categoria specificata |
| sscanf | Legge i dati formattati dalla stringa |
| strfind | Trova una stringa all'interno di un'altra |
| strrep | Trova e sostituisci la sottostringa |
| strsplit | Stringa di divisione al delimitatore specificato |
| strtok | Parti di corda selezionate |
| validatestring | Verifica la validità della stringa di testo |
| symvar | Determina le variabili simboliche nell'espressione |
| regexp | Trova espressione regolare (distingue tra maiuscole e minuscole) |
| regexpi | Trova espressione regolare (senza distinzione tra maiuscole e minuscole) |
| regexprep | Sostituisci la stringa usando l'espressione regolare |
| regexptranslate | Traduci la stringa in un'espressione regolare |
| Funzioni per il confronto delle stringhe | |
| strcmp | Confronta stringhe (distingue tra maiuscole e minuscole) |
| strcmpi | Confronta stringhe (senza distinzione tra maiuscole e minuscole) |
| strncmp | Confronta i primi n caratteri di stringhe (distingue tra maiuscole e minuscole) |
| strncmpi | Confronta i primi n caratteri di stringhe (senza distinzione tra maiuscole e minuscole) |
| Funzioni per cambiare la stringa in maiuscolo o minuscolo, creando o rimuovendo spazi bianchi | |
| deblank | Rimuovi gli spazi finali dalla fine della stringa |
| strtrim | Rimuovi lo spazio bianco iniziale e finale dalla stringa |
| inferiore | Converti la stringa in minuscolo |
| superiore | Converte la stringa in maiuscolo |
| strjust | Giustifica la matrice di caratteri |
Esempi
I seguenti esempi illustrano alcune delle funzioni di stringa sopra menzionate:
Formattazione delle stringhe
Crea un file di script e digita il seguente codice al suo interno:
A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)Quando si esegue il file, viene visualizzato il seguente risultato:
ans = 3141.592654
3141.59
+3141.59
3141.59
000003141.59Unire le stringhe
Crea un file di script e digita il seguente codice al suo interno:
%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};
% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")Quando si esegue il file, viene visualizzato il seguente risultato:
str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orangeRicerca e sostituzione di stringhe
Crea un file di script e digita il seguente codice al suo interno:
students = {'Zara Ali', 'Neha Bhatnagar', ...
'Monica Malik', 'Madhu Gautam', ...
'Madhu Sharma', 'Bhawna Sharma',...
'Nuha Ali', 'Reva Dutta', ...
'Sunaina Ali', 'Sofia Kabir'};
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)Quando si esegue il file, viene visualizzato il seguente risultato:
new_student =
{
[1,1] = Poulomi Dutta
}
first_names =
{
[1,1] = Zara
[1,2] = Neha
[1,3] = Monica
[1,4] = Madhu
[1,5] = Madhu
[1,6] = Bhawna
[1,7] = Nuha
[1,8] = Reva
[1,9] = Sunaina
[1,10] = Sofia
}Confronto di stringhe
Crea un file di script e digita il seguente codice al suo interno:
str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
sprintf('%s and %s are equal', str1, str2)
else
sprintf('%s and %s are not equal', str1, str2)
endQuando si esegue il file, viene visualizzato il seguente risultato:
str1 = This is test
str2 = This is text
ans = This is test and This is text are not equalUna funzione è un gruppo di istruzioni che insieme eseguono un'attività. In MATLAB, le funzioni sono definite in file separati. Il nome del file e della funzione dovrebbero essere gli stessi.
Le funzioni operano su variabili all'interno del proprio spazio di lavoro, chiamato anche local workspace, separato dallo spazio di lavoro a cui accedi dal prompt dei comandi di MATLAB, chiamato base workspace.
Le funzioni possono accettare più di un argomento di input e possono restituire più di un argomento di output.
La sintassi di un'istruzione di funzione è:
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)Esempio
La seguente funzione denominata mymax dovrebbe essere scritta in un file denominato mymax.m . Richiede cinque numeri come argomento e restituisce il massimo dei numeri.
Crea un file funzione, chiamato mymax.m e digita il seguente codice in esso -
function max = mymax(n1, n2, n3, n4, n5)
%This function calculates the maximum of the
% five numbers given as input
max = n1;
if(n2 > max)
max = n2;
end
if(n3 > max)
max = n3;
end
if(n4 > max)
max = n4;
end
if(n5 > max)
max = n5;
endLa prima riga di una funzione inizia con la parola chiave function. Fornisce il nome della funzione e l'ordine degli argomenti. Nel nostro esempio, la funzione mymax ha cinque argomenti di input e un argomento di output.
Le righe di commento che vengono subito dopo l'istruzione della funzione forniscono il testo della guida. Queste righe vengono stampate durante la digitazione:
help mymaxMATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
This function calculates the maximum of the
five numbers given as inputPuoi chiamare la funzione come -
mymax(34, 78, 89, 23, 11)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 89Funzioni anonime
Una funzione anonima è come una funzione inline nei linguaggi di programmazione tradizionali, definita all'interno di una singola istruzione MATLAB. Consiste in una singola espressione MATLAB e un numero qualsiasi di argomenti di input e output.
Puoi definire una funzione anonima direttamente dalla riga di comando di MATLAB o all'interno di una funzione o uno script.
In questo modo puoi creare semplici funzioni senza dover creare un file per esse.
La sintassi per creare una funzione anonima da un'espressione è
f = @(arglist)expressionEsempio
In questo esempio, scriveremo una funzione anonima chiamata power, che prenderà due numeri come input e restituirà il primo numero elevato alla potenza del secondo numero.
Crea un file di script e digita il seguente codice al suo interno:
power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)Quando esegui il file, viene visualizzato:
result1 = 343
result2 = 7
result3 = 1.0000e-10
result4 = 9.5459Funzioni primarie e secondarie
Qualsiasi funzione diversa da una funzione anonima deve essere definita all'interno di un file. Ogni file di funzione contiene una funzione primaria richiesta che appare per prima e un numero qualsiasi di sotto-funzioni opzionali che viene dopo la funzione primaria e da essa utilizzate.
Le funzioni primarie possono essere chiamate dall'esterno del file che le definisce, dalla riga di comando o da altre funzioni, ma le sotto-funzioni non possono essere chiamate dalla riga di comando o da altre funzioni, dall'esterno del file di funzione.
Le sotto-funzioni sono visibili solo alla funzione primaria e ad altre sotto-funzioni all'interno del file di funzione che le definisce.
Esempio
Scriviamo una funzione chiamata quadratica che calcoli le radici di un'equazione quadratica. La funzione richiederebbe tre input, il coefficiente quadratico, il coefficiente lineare e il termine costante. Restituirebbe le radici.
Il file di funzione quadratic.m conterrà la funzione principale quadratic e la sub-funzione disco , che calcola il discriminante.
Crea un file funzione quadratic.m e digita il seguente codice al suo interno -
function [x1,x2] = quadratic(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-functionPuoi chiamare la funzione sopra dal prompt dei comandi come -
quadratic(2,4,-4)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 0.7321Funzioni annidate
È possibile definire funzioni all'interno del corpo di un'altra funzione. Queste sono chiamate funzioni annidate. Una funzione annidata contiene uno o tutti i componenti di qualsiasi altra funzione.
Le funzioni annidate sono definite nell'ambito di un'altra funzione e condividono l'accesso allo spazio di lavoro della funzione contenitore.
Una funzione nidificata segue la seguente sintassi:
function x = A(p1, p2)
...
B(p2)
function y = B(p3)
...
end
...
endEsempio
Riscriviamo la funzione quadratic , dall'esempio precedente, tuttavia, questa volta la funzione disco sarà una funzione annidata.
Crea un file funzione quadratic2.m e digita il seguente codice al suo interno -
function [x1,x2] = quadratic2(a,b,c)
function disc % nested function
d = sqrt(b^2 - 4*a*c);
end % end of function disc
disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of function quadratic2Puoi chiamare la funzione sopra dal prompt dei comandi come -
quadratic2(2,4,-4)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 0.73205Funzioni private
Una funzione privata è una funzione primaria visibile solo a un gruppo limitato di altre funzioni. Se non si desidera esporre l'implementazione di una o più funzioni, è possibile crearle come funzioni private.
Le funzioni private risiedono in subfolders con il nome speciale private.
Sono visibili solo alle funzioni nella cartella principale.
Esempio
Riscriviamo la funzione quadratica . Questa volta, tuttavia, la funzione del disco che calcola il discriminante, sarà una funzione privata.
Crea una sottocartella denominata private nella directory di lavoro. Memorizza il seguente file funzione disc.m in esso -
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-functionCrea una funzione quadratic3.m nella tua directory di lavoro e digita il seguente codice in essa -
function [x1,x2] = quadratic3(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic3Puoi chiamare la funzione sopra dal prompt dei comandi come -
quadratic3(2,4,-4)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans = 0.73205Variabili globali
Le variabili globali possono essere condivise da più di una funzione. Per questo, è necessario dichiarare la variabile come globale in tutte le funzioni.
Se desideri accedere a quella variabile dallo spazio di lavoro di base, dichiara la variabile nella riga di comando.
La dichiarazione globale deve avvenire prima che la variabile venga effettivamente utilizzata in una funzione. È buona norma utilizzare lettere maiuscole per i nomi delle variabili globali per distinguerle dalle altre variabili.
Esempio
Creiamo un file di funzione chiamato average.m e digitiamo il seguente codice al suo interno -
function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
endCrea un file di script e digita il seguente codice al suo interno:
global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)Quando esegui il file, verrà visualizzato il seguente risultato:
av = 35.500Importare dati in MATLAB significa caricare dati da un file esterno. Ilimportdatala funzione consente di caricare vari file di dati di diversi formati. Ha le seguenti cinque forme:
| Sr.No. | Descrizione della funzione |
|---|---|
| 1 | A = importdata(filename) Carica i dati nell'array A dal file indicato con nome file . |
| 2 | A = importdata('-pastespecial') Carica i dati dagli appunti di sistema piuttosto che da un file. |
| 3 | A = importdata(___, delimiterIn) Interpreta delimiterIn come separatore di colonna nel file ASCII, nel nome del file o nei dati degli appunti. È possibile utilizzare delimiterIn con uno qualsiasi degli argomenti di input nelle sintassi precedenti. |
| 4 | A = importdata(___, delimiterIn, headerlinesIn) Carica i dati dal file ASCII, dal nome del file o dagli appunti, leggendo i dati numerici a partire dalle intestazioni di riga In + 1 . |
| 5 | [A, delimiterOut, headerlinesOut] = importdata(___) Restituisce il carattere delimitatore rilevato per il file ASCII di input in delimiterOut e il numero rilevato di righe di intestazione in headerlinesOut , utilizzando uno degli argomenti di input nelle sintassi precedenti. |
Per impostazione predefinita, Octave non supporta la funzione importdata () , quindi dovrai cercare e installare questo pacchetto per far funzionare i seguenti esempi con la tua installazione di Octave.
Esempio 1
Carichiamo e visualizziamo un file immagine. Crea un file di script e digita il seguente codice al suo interno:
filename = 'smile.jpg';
A = importdata(filename);
image(A);Quando esegui il file, MATLAB visualizza il file immagine. Tuttavia, è necessario memorizzarlo nella directory corrente.

Esempio 2
In questo esempio, importiamo un file di testo e specifichiamo Delimitatore e Intestazione colonna. Creiamo un file ASCII delimitato da spazi con intestazioni di colonna, denominato settimanaledata.txt .
Il nostro file di testo Weeklydata.txt ha questo aspetto:
SunDay MonDay TuesDay WednesDay ThursDay FriDay SaturDay
95.01 76.21 61.54 40.57 55.79 70.28 81.53
73.11 45.65 79.19 93.55 75.29 69.87 74.68
60.68 41.85 92.18 91.69 81.32 90.38 74.51
48.60 82.14 73.82 41.03 0.99 67.22 93.18
89.13 44.47 57.63 89.36 13.89 19.88 46.60Crea un file di script e digita il seguente codice al suo interno:
filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);
% View data
for k = [1:7]
disp(A.colheaders{1, k})
disp(A.data(:, k))
disp(' ')
endQuando si esegue il file, viene visualizzato il seguente risultato:
SunDay
95.0100
73.1100
60.6800
48.6000
89.1300
MonDay
76.2100
45.6500
41.8500
82.1400
44.4700
TuesDay
61.5400
79.1900
92.1800
73.8200
57.6300
WednesDay
40.5700
93.5500
91.6900
41.0300
89.3600
ThursDay
55.7900
75.2900
81.3200
0.9900
13.8900
FriDay
70.2800
69.8700
90.3800
67.2200
19.8800
SaturDay
81.5300
74.6800
74.5100
93.1800
46.6000Esempio 3
In questo esempio, importiamo i dati dagli appunti.
Copia le seguenti righe negli appunti:
Mathematics is simple
Crea un file di script e digita il codice seguente:
A = importdata('-pastespecial')Quando si esegue il file, viene visualizzato il seguente risultato:
A =
'Mathematics is simple'I / O file di basso livello
La funzione importdata è una funzione di alto livello. Le funzioni di I / O su file di basso livello in MATLAB consentono il massimo controllo sulla lettura o la scrittura di dati in un file. Tuttavia, queste funzioni richiedono informazioni più dettagliate sul file per funzionare in modo efficiente.
MATLAB fornisce le seguenti funzioni per le operazioni di lettura e scrittura a livello di byte o carattere:
| Funzione | Descrizione |
|---|---|
| fclose | Chiudi uno o tutti i file aperti |
| feof | Test per la fine del file |
| ferror | Informazioni sugli errori di I / O dei file |
| fgetl | Legge la riga dal file, rimuovendo i caratteri di nuova riga |
| fgets | Legge la riga dal file, mantenendo i caratteri di nuova riga |
| fopen | Apri file o ottieni informazioni sui file aperti |
| fprintf | Scrivi i dati in un file di testo |
| fread | Legge i dati dal file binario |
| frewind | Sposta l'indicatore di posizione del file all'inizio del file aperto |
| fscanf | Leggi i dati dal file di testo |
| fseek | Sposta nella posizione specificata nel file |
| ftell | Posizione nel file aperto |
| fwrite | Scrive i dati in un file binario |
Importa file di dati di testo con I / O di basso livello
MATLAB fornisce le seguenti funzioni per l'importazione di basso livello di file di dati di testo:
Il fscanf la funzione legge i dati formattati in un file di testo o ASCII.
Il fgetl e fgets le funzioni leggono una riga di un file alla volta, dove un carattere di nuova riga separa ogni riga.
Il fread la funzione legge un flusso di dati a livello di byte o bit.
Esempio
Abbiamo un file di dati di testo "myfile.txt" salvato nella nostra directory di lavoro. Il file memorizza i dati sulle precipitazioni per tre mesi; Giugno, luglio e agosto per l'anno 2012.
I dati in miofile.txt contengono serie ripetute di misurazioni di ora, mese e precipitazioni in cinque punti. I dati dell'intestazione memorizzano il numero di mesi M; quindi abbiamo M set di misurazioni.
Il file ha questo aspetto:
Rainfall Data
Months: June, July, August
M = 3
12:00:00
June-2012
17.21 28.52 39.78 16.55 23.67
19.15 0.35 17.57 NaN 12.01
17.92 28.49 17.40 17.06 11.09
9.59 9.33 NaN 0.31 0.23
10.46 13.17 NaN 14.89 19.33
20.97 19.50 17.65 14.45 14.00
18.23 10.34 17.95 16.46 19.34
09:10:02
July-2012
12.76 16.94 14.38 11.86 16.89
20.46 23.17 NaN 24.89 19.33
30.97 49.50 47.65 24.45 34.00
18.23 30.34 27.95 16.46 19.34
30.46 33.17 NaN 34.89 29.33
30.97 49.50 47.65 24.45 34.00
28.67 30.34 27.95 36.46 29.34
15:03:40
August-2012
17.09 16.55 19.59 17.25 19.22
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67Importeremo i dati da questo file e visualizzeremo questi dati. Procedi nel seguente modo:
Apri il file con fopen funzione e ottenere l'identificatore del file.
Descrivi i dati nel file con format specifiers, ad esempio '%s"per una stringa,"%d"per un numero intero o"%f'per un numero in virgola mobile.
Per saltare i caratteri letterali nel file, includerli nella descrizione del formato. Per saltare un campo dati, utilizza un asterisco ("*") nello specificatore.
Ad esempio, per leggere le intestazioni e restituire il singolo valore per M, scriviamo -
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);Per impostazione predefinita, fscanflegge i dati in base alla nostra descrizione del formato fino a quando non trova alcuna corrispondenza per i dati o raggiunge la fine del file. Qui useremo il ciclo for per leggere 3 set di dati e ogni volta leggerà 7 righe e 5 colonne.
Creeremo una struttura denominata mydata nell'area di lavoro per memorizzare i dati letti dal file. Questa struttura ha tre campi: ora , mese e array raindata .
Crea un file di script e digita il seguente codice al suo interno:
filename = '/data/myfile.txt';
rows = 7;
cols = 5;
% open the file
fid = fopen(filename);
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
% read each set of measurements
for n = 1:M
mydata(n).time = fscanf(fid, '%s', 1);
mydata(n).month = fscanf(fid, '%s', 1);
% fscanf fills the array in column order,
% so transpose the results
mydata(n).raindata = ...
fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
disp(mydata(n).time), disp(mydata(n).month)
disp(mydata(n).raindata)
end
% close the file
fclose(fid);Quando si esegue il file, viene visualizzato il seguente risultato:
12:00:00
June-2012
17.2100 17.5700 11.0900 13.1700 14.4500
28.5200 NaN 9.5900 NaN 14.0000
39.7800 12.0100 9.3300 14.8900 18.2300
16.5500 17.9200 NaN 19.3300 10.3400
23.6700 28.4900 0.3100 20.9700 17.9500
19.1500 17.4000 0.2300 19.5000 16.4600
0.3500 17.0600 10.4600 17.6500 19.3400
09:10:02
July-2012
12.7600 NaN 34.0000 33.1700 24.4500
16.9400 24.8900 18.2300 NaN 34.0000
14.3800 19.3300 30.3400 34.8900 28.6700
11.8600 30.9700 27.9500 29.3300 30.3400
16.8900 49.5000 16.4600 30.9700 27.9500
20.4600 47.6500 19.3400 49.5000 36.4600
23.1700 24.4500 30.4600 47.6500 29.3400
15:03:40
August-2012
17.0900 13.4800 27.2100 11.4500 25.0500
16.5500 22.5500 26.7900 13.4800 27.2100
19.5900 24.0100 24.9800 22.5500 26.7900
17.2500 NaN 12.2300 24.0100 24.9800
19.2200 21.1900 16.9900 NaN 12.2300
17.5400 25.8500 18.6700 21.1900 16.9900
11.4500 25.0500 17.5400 25.8500 18.6700L'esportazione (o l'output) dei dati in MATLAB significa scrivere in file. MATLAB ti consente di utilizzare i tuoi dati in un'altra applicazione che legge i file ASCII. Per questo, MATLAB fornisce diverse opzioni di esportazione dei dati.
È possibile creare il seguente tipo di file:
File di dati ASCII rettangolare e delimitato da un array.
File di diario (o registro) delle sequenze di tasti e output di testo risultante.
File ASCII specializzato che utilizza funzioni di basso livello come fprintf.
File MEX per accedere alla routine C / C ++ o Fortran che scrive in un particolare formato di file di testo.
Oltre a questo, puoi anche esportare i dati su fogli di calcolo.
Esistono due modi per esportare un array numerico come file di dati ASCII delimitato:
Usando il save e specificando la -ascii qualificatore
Usando il dlmwrite funzione
La sintassi per l'utilizzo della funzione di salvataggio è:
save my_data.out num_array -asciidove, my_data.out è il file di dati ASCII delimitato creato, num_array è un array numerico e−ascii è lo specificatore.
Sintassi per l'utilizzo di dlmwrite la funzione è -
dlmwrite('my_data.out', num_array, 'dlm_char')dove, my_data.out è il file di dati ASCII delimitato creato, num_array è un array numerico e dlm_char è il carattere delimitatore.
Esempio
Il seguente esempio dimostra il concetto. Crea un file di script e digita il codice seguente:
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.outQuando si esegue il file, viene visualizzato il seguente risultato:
1.0000000e+00 2.0000000e+00 3.0000000e+00 4.0000000e+00
4.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00
7.0000000e+00 8.0000000e+00 9.0000000e+00 0.0000000e+00
1 2 3 4
4 5 6 7
7 8 9 0Si noti che il comando save -ascii e la funzione dlmwrite non funzionano con gli array di celle come input. Per creare un file ASCII delimitato dal contenuto di un array di celle, puoi farlo
In alternativa, converti l'array di celle in una matrice utilizzando l'estensione cell2mat funzione
Oppure esportare la matrice di celle utilizzando le funzioni di I / O di file di basso livello.
Se usi l'estensione save funzione per scrivere un array di caratteri in un file ASCII, scrive l'equivalente ASCII dei caratteri nel file.
Ad esempio, scriviamo la parola "ciao" in un file:
h = 'hello';
save textdata.out h -ascii
type textdata.outMATLAB esegue le istruzioni precedenti e visualizza il seguente risultato. che sono i caratteri della stringa "ciao" in formato ASCII a 8 cifre.
1.0400000e+02 1.0100000e+02 1.0800000e+02 1.0800000e+02 1.1100000e+02Scrivere su file di diario
I file di diario sono registri delle attività della tua sessione MATLAB. La funzione diario crea una copia esatta della sessione in un file su disco, escluse le immagini.
Per attivare la funzione diario, digita -
diaryFacoltativamente, puoi dare il nome del file di registro, ad esempio -
diary logdata.outPer disattivare la funzione diario:
diary offPuoi aprire il file del diario in un editor di testo.
Esportazione di dati in file di dati di testo con I / O di basso livello
Finora abbiamo esportato array numerici. Tuttavia, potrebbe essere necessario creare altri file di testo, comprese combinazioni di dati numerici e di caratteri, file di output non rettangolari o file con schemi di codifica non ASCII. Per questi scopi, MATLAB fornisce il livello bassofprintf funzione.
Come nelle attività di file di I / O di basso livello, prima di esportare, è necessario aprire o creare un file con l'estensione fopenfunzione e ottenere l'identificatore del file. Per impostazione predefinita, fopen apre un file per l'accesso in sola lettura. È necessario specificare l'autorizzazione per scrivere o aggiungere, ad esempio "w" o "a".
Dopo aver elaborato il file, è necessario chiuderlo con fclose(fid) funzione.
Il seguente esempio dimostra il concetto:
Esempio
Crea un file di script e digita il seguente codice al suo interno:
% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
% open a file for writing
fid = fopen('logtable.txt', 'w');
% Table Header
fprintf(fid, 'Log Function\n\n');
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f %f\n', y);
fclose(fid);
% display the file created
type logtable.txtQuando si esegue il file, viene visualizzato il seguente risultato:
Log Function
0.000000 -Inf
10.000000 2.302585
20.000000 2.995732
30.000000 3.401197
40.000000 3.688879
50.000000 3.912023
60.000000 4.094345
70.000000 4.248495
80.000000 4.382027
90.000000 4.499810
100.000000 4.605170Per tracciare il grafico di una funzione, è necessario eseguire i seguenti passaggi:
Definire x, specificando il range of values per la variabile x, per cui deve essere tracciata la funzione
Definisci la funzione, y = f(x)
Chiama il plot comando, come plot(x, y)
L'esempio seguente dimostrerebbe il concetto. Tracciamo la funzione semplicey = x per l'intervallo di valori per x da 0 a 100, con un incremento di 5.
Crea un file di script e digita il codice seguente:
x = [0:5:100];
y = x;
plot(x, y)Quando esegui il file, MATLAB mostra il seguente grafico:

Prendiamo un altro esempio per tracciare la funzione y = x 2 . In questo esempio, disegneremo due grafici con la stessa funzione, ma nella seconda volta, ridurremo il valore di incremento. Si noti che diminuendo l'incremento, il grafico diventa più fluido.
Crea un file di script e digita il codice seguente:
x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:20:100];
y = x.^2;
plot(x, y)Quando esegui il file, MATLAB mostra il seguente grafico:
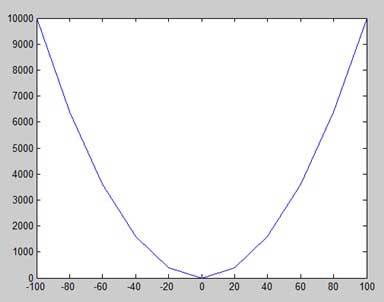
Cambia leggermente il file di codice, riduci l'incremento a 5 -
x = [-100:5:100];
y = x.^2;
plot(x, y)MATLAB traccia un grafico più fluido -
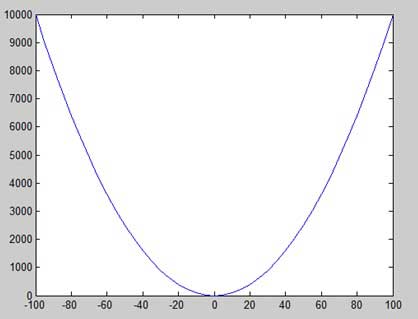
Aggiunta di titolo, etichette, linee della griglia e scala sul grafico
MATLAB ti consente di aggiungere titolo, etichette lungo l'asse xe l'asse y, linee della griglia e anche di regolare gli assi per abbellire il grafico.
Il xlabel e ylabel i comandi generano etichette lungo l'asse xe l'asse y.
Il title Il comando ti permette di inserire un titolo nel grafico.
Il grid on Il comando consente di inserire le linee della griglia sul grafico.
Il axis equal il comando permette di generare il grafico con gli stessi fattori di scala e gli spazi su entrambi gli assi.
Il axis square il comando genera un grafico quadrato.
Esempio
Crea un file di script e digita il codice seguente:
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equalMATLAB genera il seguente grafico:
Disegnare più funzioni sullo stesso grafico
Puoi disegnare più grafici sullo stesso grafico. Il seguente esempio dimostra il concetto:
Esempio
Crea un file di script e digita il codice seguente:
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')MATLAB genera il seguente grafico:
Impostazione dei colori sul grafico
MATLAB fornisce otto opzioni di colore di base per disegnare grafici. La tabella seguente mostra i colori e i relativi codici:
| Codice | Colore |
|---|---|
| w | bianca |
| K | Nero |
| b | Blu |
| r | Rosso |
| c | Ciano |
| g | verde |
| m | Magenta |
| y | Giallo |
Esempio
Disegniamo il grafico di due polinomi
f (x) = 3x 4 + 2x 3 + 7x 2 + 2x + 9 e
g (x) = 5x 3 + 9x + 2
Crea un file di script e digita il codice seguente:
x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')Quando esegui il file, MATLAB genera il seguente grafico:
Impostazione delle scale degli assi
Il axisil comando consente di impostare le scale degli assi. È possibile fornire i valori minimi e massimi per gli assi xey utilizzando il comando assi nel modo seguente:
axis ( [xmin xmax ymin ymax] )L'esempio seguente mostra questo:
Esempio
Crea un file di script e digita il codice seguente:
x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])Quando esegui il file, MATLAB genera il seguente grafico:
Generazione di sotto-grafici
Quando crei una serie di grafici nella stessa figura, ognuno di questi grafici viene chiamato sottotrama. Ilsubplot comando viene utilizzato per creare sottotrame.
La sintassi del comando è:
subplot(m, n, p)dove, m e n sono il numero di righe e colonne della matrice del grafico e p specifica dove mettere un particolare grafico.
Ogni grafico creato con il comando sottotrama può avere le proprie caratteristiche. L'esempio seguente dimostra il concetto:
Esempio
Generiamo due grafici:
y = e −1,5x sin (10x)
y = e −2x sin (10x)
Crea un file di script e digita il codice seguente:
x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])Quando esegui il file, MATLAB genera il seguente grafico:
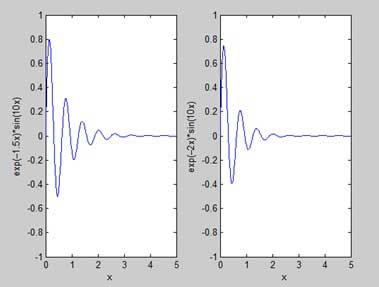
Questo capitolo continuerà ad esplorare le capacità di stampa e grafica di MATLAB. Discuteremo -
- Disegno di grafici a barre
- Disegnare contorni
- Trame tridimensionali
Disegno di grafici a barre
Il barIl comando disegna un grafico a barre bidimensionale. Facciamo un esempio per dimostrare l'idea.
Esempio
Facciamo una classe immaginaria con 10 studenti. Sappiamo che la percentuale di voti ottenuti da questi studenti è 75, 58, 90, 87, 50, 85, 92, 75, 60 e 95. Tracciamo il grafico a barre per questi dati.
Crea un file di script e digita il codice seguente:
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.epsQuando esegui il file, MATLAB mostra il seguente grafico a barre:

Disegnare contorni
Una linea di contorno di una funzione di due variabili è una curva lungo la quale la funzione ha un valore costante. Le curve di livello vengono utilizzate per creare mappe di contorno unendo punti di uguale elevazione sopra un dato livello, come il livello medio del mare.
MATLAB fornisce un file contour funzione per disegnare mappe di contorno.
Esempio
Generiamo una mappa di contorno che mostra le curve di livello per una data funzione g = f (x, y). Questa funzione ha due variabili. Quindi, dovremo generare due variabili indipendenti, cioè due set di dati x e y. Questo viene fatto chiamando ilmeshgrid comando.
Il meshgrid comando viene utilizzato per generare una matrice di elementi che forniscono l'intervallo su xey insieme alla specifica di incremento in ogni caso.
Tracciamo la nostra funzione g = f (x, y), dove −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Prendiamo un incremento di 0,1 per entrambi i valori. Le variabili sono impostate come -
[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);Infine, dobbiamo assegnare la funzione. Sia la nostra funzione: x 2 + y 2
Crea un file di script e digita il codice seguente:
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
contour(x,y,g) % call the contour function
print -deps graph.epsQuando esegui il file, MATLAB visualizza la seguente mappa di contorno:
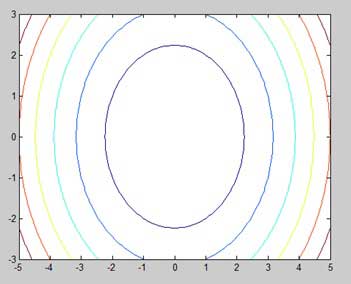
Modifichiamo un po 'il codice per abbellire la mappa
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
[C, h] = contour(x,y,g); % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.epsQuando esegui il file, MATLAB visualizza la seguente mappa di contorno:
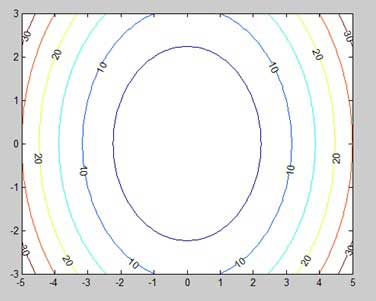
Grafici tridimensionali
I grafici tridimensionali mostrano fondamentalmente una superficie definita da una funzione in due variabili, g = f (x, y).
Come prima, per definire g, creiamo prima un insieme di punti (x, y) sul dominio della funzione usando il meshgridcomando. Successivamente, assegniamo la funzione stessa. Infine, usiamo ilsurf comando per creare un grafico di superficie.
Il seguente esempio dimostra il concetto:
Esempio
Creiamo una mappa della superficie 3D per la funzione g = xe - (x 2 + y 2 )
Crea un file di script e digita il codice seguente:
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.epsQuando esegui il file, MATLAB mostra la seguente mappa 3-D:

Puoi anche usare il file meshcomando per generare una superficie tridimensionale. in ogni caso, ilsurf Il comando visualizza sia le linee di collegamento che le facce della superficie a colori, mentre il mesh Il comando crea una superficie wireframe con linee colorate che collegano i punti di definizione.
Finora, abbiamo visto che tutti gli esempi funzionano in MATLAB così come il suo GNU, chiamato in alternativa Octave. Ma per risolvere le equazioni algebriche di base, sia MATLAB che Octave sono leggermente diversi, quindi proveremo a trattare MATLAB e Octave in sezioni separate.
Discuteremo anche la fattorizzazione e la semplificazione delle espressioni algebriche.
Risoluzione di equazioni algebriche di base in MATLAB
Il solveè usata per risolvere equazioni algebriche. Nella sua forma più semplice, la funzione di risoluzione accetta l'equazione racchiusa tra virgolette come argomento.
Ad esempio, risolviamo x nell'equazione x-5 = 0
solve('x-5=0')MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
5Puoi anche chiamare la funzione di risoluzione come -
y = solve('x-5 = 0')MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
y =
5Potresti anche non includere il lato destro dell'equazione -
solve('x-5')MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
5Se l'equazione coinvolge più simboli, MATLAB per impostazione predefinita presume che tu stia risolvendo per x, tuttavia, la funzione di risoluzione ha un'altra forma:
solve(equation, variable)dove puoi anche menzionare la variabile.
Ad esempio, risolviamo l'equazione v - u - 3t 2 = 0, per v. In questo caso, dovremmo scrivere -
solve('v-u-3*t^2=0', 'v')MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
3*t^2 + uRisoluzione di equazioni algebriche di base in ottava
Il roots è usata per risolvere equazioni algebriche in Octave e puoi scrivere sopra gli esempi come segue:
Ad esempio, risolviamo x nell'equazione x-5 = 0
roots([1, -5])Octave eseguirà l'istruzione precedente e restituirà il seguente risultato:
ans = 5Puoi anche chiamare la funzione di risoluzione come -
y = roots([1, -5])Octave eseguirà l'istruzione precedente e restituirà il seguente risultato:
y = 5Risoluzione di equazioni quadratiche in MATLAB
Il solvepuò anche risolvere equazioni di ordine superiore. Viene spesso utilizzato per risolvere equazioni quadratiche. La funzione restituisce le radici dell'equazione in un array.
L'esempio seguente risolve l'equazione quadratica x 2 -7x +12 = 0. Crea un file di script e digita il codice seguente:
eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));Quando si esegue il file, viene visualizzato il seguente risultato:
The first root is:
3
The second root is:
4Risoluzione di equazioni quadratiche in ottava
L'esempio seguente risolve l'equazione quadratica x 2 -7x +12 = 0 in Ottava. Crea un file di script e digita il codice seguente:
s = roots([1, -7, 12]);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));Quando si esegue il file, viene visualizzato il seguente risultato:
The first root is:
4
The second root is:
3Risoluzione di equazioni di ordine superiore in MATLAB
Il solvepuò anche risolvere equazioni di ordine superiore. Ad esempio, risolviamo un'equazione cubica come (x-3) 2 (x-7) = 0
solve('(x-3)^2*(x-7)=0')MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
3
3
7In caso di equazioni di ordine superiore, le radici sono lunghe e contengono molti termini. È possibile ottenere il valore numerico di tali radici convertendole in doppie. L'esempio seguente risolve l'equazione del quarto ordine x 4 - 7x 3 + 3x 2 - 5x + 9 = 0.
Crea un file di script e digita il codice seguente:
eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));Quando esegui il file, restituisce il seguente risultato:
The first root is:
6.630396332390718431485053218985
The second root is:
1.0597804633025896291682772499885
The third root is:
- 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i
The fourth root is:
- 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i
Numeric value of first root
6.6304
Numeric value of second root
1.0598
Numeric value of third root
-0.3451 - 1.0778i
Numeric value of fourth root
-0.3451 + 1.0778iSi noti che le ultime due radici sono numeri complessi.
Risoluzione di equazioni di ordine superiore in ottava
L'esempio seguente risolve l'equazione del quarto ordine x 4 - 7x 3 + 3x 2 - 5x + 9 = 0.
Crea un file di script e digita il codice seguente:
v = [1, -7, 3, -5, 9];
s = roots(v);
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));Quando esegui il file, restituisce il seguente risultato:
Numeric value of first root
6.6304
Numeric value of second root
-0.34509 + 1.07784i
Numeric value of third root
-0.34509 - 1.07784i
Numeric value of fourth root
1.0598Risoluzione di sistemi di equazioni in MATLAB
Il solvepuò essere utilizzata anche per generare soluzioni di sistemi di equazioni che coinvolgono più di una variabile. Facciamo un semplice esempio per dimostrare questo uso.
Risolviamo le equazioni -
5x + 9y = 5
3x - 6y = 4
Crea un file di script e digita il codice seguente:
s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.yQuando si esegue il file, viene visualizzato il seguente risultato:
ans =
22/19
ans =
-5/57Allo stesso modo, puoi risolvere sistemi lineari più grandi. Considera il seguente insieme di equazioni:
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Risolvere il sistema di equazioni in ottava
Abbiamo un approccio leggermente diverso per risolvere un sistema di 'n' equazioni lineari in 'n' incognite. Facciamo un semplice esempio per dimostrare questo uso.
Risolviamo le equazioni -
5x + 9y = 5
3x - 6y = 4
Un tale sistema di equazioni lineari può essere scritto come l'equazione a matrice singola Ax = b, dove A è la matrice dei coefficienti, b è il vettore colonna contenente il lato destro delle equazioni lineari ex è il vettore colonna che rappresenta la soluzione come mostrato nel programma seguente -
Crea un file di script e digita il codice seguente:
A = [5, 9; 3, -6];
b = [5;4];
A \ bQuando si esegue il file, viene visualizzato il seguente risultato:
ans =
1.157895
-0.087719Allo stesso modo, puoi risolvere sistemi lineari più grandi come indicato di seguito:
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Espansione e raccolta di equazioni in MATLAB
Il expand e il collectfunzione espande e raccoglie rispettivamente un'equazione. Il seguente esempio dimostra i concetti:
Quando lavori con molte funzioni simboliche, dovresti dichiarare che le tue variabili sono simboliche.
Crea un file di script e digita il codice seguente:
syms x %symbolic variable x
syms y %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))Quando si esegue il file, viene visualizzato il seguente risultato:
ans =
x^2 + 4*x - 45
ans =
x^4 + x^3 - 43*x^2 + 23*x + 210
ans =
2*cos(x)*sin(x)
ans =
cos(x)*cos(y) - sin(x)*sin(y)
ans =
x^4 - 7*x^3
ans =
x^6 - 8*x^5 + 15*x^4Espansione e raccolta di equazioni in ottava
Hai bisogno di avere symbolic pacchetto, che fornisce expand e il collectfunzione per espandere e raccogliere un'equazione, rispettivamente. Il seguente esempio dimostra i concetti:
Quando lavori con molte funzioni simboliche, dovresti dichiarare che le tue variabili sono simboliche ma Octave ha un approccio diverso per definire le variabili simboliche. Notare l'uso diSin e Cos, che sono anche definiti nel pacchetto simbolico.
Crea un file di script e digita il codice seguente:
% first of all load the package, make sure its installed.
pkg load symbolic
% make symbols module available
symbols
% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)Quando si esegue il file, viene visualizzato il seguente risultato:
ans =
-45.0+x^2+(4.0)*x
ans =
210.0+x^4-(43.0)*x^2+x^3+(23.0)*x
ans =
sin((2.0)*x)
ans =
cos(y+x)
ans =
x^(3.0)*(-7.0+x)
ans =
(-3.0+x)*x^(4.0)*(-5.0+x)Fattorizzazione e semplificazione delle espressioni algebriche
Il factor funzione fattorizza un'espressione e il simplifyfunzione semplifica un'espressione. Il seguente esempio dimostra il concetto:
Esempio
Crea un file di script e digita il codice seguente:
syms x
syms y
factor(x^3 - y^3)
factor([x^2-y^2,x^3+y^3])
simplify((x^4-16)/(x^2-4))Quando si esegue il file, viene visualizzato il seguente risultato:
ans =
(x - y)*(x^2 + x*y + y^2)
ans =
[ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)]
ans =
x^2 + 4MATLAB fornisce vari modi per risolvere problemi di calcolo differenziale e integrale, risolvere equazioni differenziali di qualsiasi grado e calcolo dei limiti. Soprattutto, puoi facilmente tracciare i grafici di funzioni complesse e controllare i massimi, i minimi e altri punti di cancelleria su un grafico risolvendo la funzione originale, così come la sua derivata.
Questo capitolo tratterà i problemi del calcolo. In questo capitolo discuteremo i concetti del pre-calcolo, ovvero il calcolo dei limiti delle funzioni e la verifica delle proprietà dei limiti.
Nel prossimo capitolo Differenziale , calcoleremo la derivata di un'espressione e troveremo i massimi e minimi locali su un grafico. Discuteremo anche la risoluzione di equazioni differenziali.
Infine, nel capitolo sull'integrazione , discuteremo del calcolo integrale.
Calcolo dei limiti
MATLAB fornisce il limitfunzione per il calcolo dei limiti. Nella sua forma più semplice, illimit la funzione accetta l'espressione come argomento e trova il limite dell'espressione quando la variabile indipendente va a zero.
Ad esempio, calcoliamo il limite di una funzione f (x) = (x 3 + 5) / (x 4 + 7), poiché x tende a zero.
syms x
limit((x^3 + 5)/(x^4 + 7))MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
5/7La funzione limite rientra nel regno del calcolo simbolico; devi usare il filesymsfunzione per dire a MATLAB quali variabili simboliche stai utilizzando. Puoi anche calcolare il limite di una funzione, poiché la variabile tende a un numero diverso da zero. Per calcolare lim x-> a (f (x)), usiamo il comando limit con argomenti. Il primo è l'espressione e il secondo è il numero, che x si avvicina, qui è a .
Ad esempio, calcoliamo il limite di una funzione f (x) = (x-3) / (x-1), poiché x tende a 1.
limit((x - 3)/(x-1),1)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
NaNFacciamo un altro esempio,
limit(x^2 + 5, 3)MATLAB eseguirà l'istruzione sopra e restituirà il seguente risultato:
ans =
14Calcolo dei limiti utilizzando Octave
Di seguito è riportata la versione Octave dell'esempio precedente utilizzando symbolic pacchetto, prova ad eseguire e confrontare il risultato -
pkg load symbolic
symbols
x = sym("x");
subs((x^3+5)/(x^4+7),x,0)Octave eseguirà l'istruzione precedente e restituirà il seguente risultato:
ans =
0.7142857142857142857Verifica delle proprietà di base dei limiti
Il Teorema algebrico del limite fornisce alcune proprietà di base dei limiti. Questi sono i seguenti:
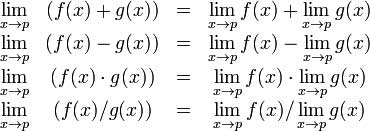
Consideriamo due funzioni:
- f (x) = (3x + 5) / (x - 3)
- g (x) = x 2 + 1.
Calcoliamo i limiti delle funzioni per x tende a 5, di entrambe le funzioni e verifichiamo le proprietà di base dei limiti utilizzando queste due funzioni e MATLAB.
Esempio
Crea un file di script e digita il seguente codice al suo interno:
syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)Quando esegui il file, viene visualizzato:
l1 =
17
l2 =
17
lAdd =
34
lSub =
0
lMult =
289
lDiv =
1Verifica delle proprietà di base dei limiti utilizzando Octave
Di seguito è riportata la versione Octave dell'esempio precedente utilizzando symbolic pacchetto, prova ad eseguire e confrontare il risultato -
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)Octave eseguirà l'istruzione precedente e restituirà il seguente risultato:
l1 =
17.0
l2 =
17.0
lAdd =
34.0
lSub =
0.0
lMult =
289.0
lDiv =
1.0Limiti dei lati sinistro e destro
Quando una funzione ha una discontinuità per un valore particolare della variabile, il limite non esiste a quel punto. In altre parole, i limiti di una funzione f (x) hanno discontinuità in x = a, quando il valore del limite, quando x si avvicina a x dal lato sinistro, non è uguale al valore del limite quando x si avvicina dal lato destro.
Questo porta al concetto di limiti per mancini e destrimani. Un limite per mancini è definito come il limite come x -> a, da sinistra, cioè x si avvicina a, per valori di x <a. Un limite destrorso è definito come il limite come x -> a, da destra, cioè x si avvicina a, per valori di x> a. Quando il limite per la mano sinistra e il limite per la mano destra non sono uguali, il limite non esiste.
Consideriamo una funzione:
f(x) = (x - 3)/|x - 3|
Mostreremo che lim x-> 3 f (x) non esiste. MATLAB ci aiuta a stabilire questo fatto in due modi:
- Tracciando il grafico della funzione e mostrando la discontinuità.
- Calcolando i limiti e dimostrando che entrambi sono diversi.
I limiti per mancini e destrimani vengono calcolati passando le stringhe di caratteri "left" e "right" al comando limit come ultimo argomento.
Esempio
Crea un file di script e digita il seguente codice al suo interno:
f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')Quando esegui il file, MATLAB disegna il seguente grafico
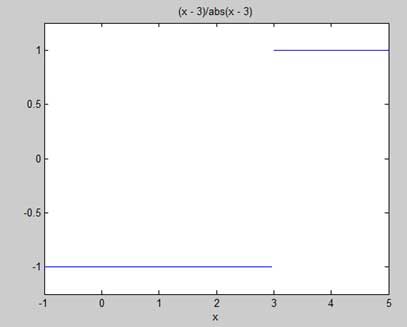
Dopo che viene visualizzato questo output seguente:
l =
-1
r =
1MATLAB fornisce il diffcomando per il calcolo delle derivate simboliche. Nella sua forma più semplice, passi la funzione che vuoi differenziare al comando diff come argomento.
Ad esempio, calcoliamo la derivata della funzione f (t) = 3t 2 + 2t -2
Esempio
Crea un file di script e digita il seguente codice al suo interno:
syms t
f = 3*t^2 + 2*t^(-2);
diff(f)Quando il codice precedente viene compilato ed eseguito, produce il seguente risultato:
ans =
6*t - 4/t^3Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)Octave esegue il codice e restituisce il seguente risultato:
ans =
-(4.0)*t^(-3.0)+(6.0)*tVerifica delle regole elementari di differenziazione
Stabiliamo brevemente varie equazioni o regole per la differenziazione delle funzioni e verifichiamo queste regole. A questo scopo, scriveremo f '(x) per una derivata del primo ordine e f "(x) per una derivata del secondo ordine.
Di seguito sono riportate le regole per la differenziazione:
Regola 1
Per ogni funzione feg e ogni numero reale aeb sono la derivata della funzione -
h(x) = af(x) + bg(x) rispetto a x è dato da -
h'(x) = af'(x) + bg'(x)
Regola 2
Il sum e subtraction le regole stabiliscono che se f e g sono due funzioni, f 'e g' sono rispettivamente le loro derivate, allora,
(f + g)' = f' + g'
(f - g)' = f' - g'
Regola 3
Il product regola afferma che se f e g sono due funzioni, f 'e g' sono le loro derivate rispettivamente, allora,
(f.g)' = f'.g + g'.f
Regola 4
Il quotient regola afferma che se f e g sono due funzioni, f 'e g' sono le loro derivate rispettivamente, allora,
(f/g)' = (f'.g - g'.f)/g2
Regola 5
Il polynomial o la regola del potere elementare afferma che, se y = f(x) = xn, poi f' = n. x(n-1)
Un risultato diretto di questa regola è che la derivata di qualsiasi costante è zero, cioè se y = k, qualsiasi costante, quindi
f' = 0
Regola 6
Il chain regola afferma che, derivata della funzione di una funzione h(x) = f(g(x)) rispetto a x is,
h'(x)= f'(g(x)).g'(x)
Esempio
Crea un file di script e digita il seguente codice al suo interno:
syms x
syms t
f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)Quando esegui il file, MATLAB mostra il seguente risultato:
f =
(x^2 + 3)*(x + 2)
der1 =
2*x*(x + 2) + x^2 + 3
f =
(t^(1/2) + t^3)*(t^2 + 3)
der2 =
(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
f =
(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 =
(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
f =
(2*x^2 + 3*x)/(x^3 + 1)
der4 =
(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
f =
(x^2 + 1)^17
der5 =
34*x*(x^2 + 1)^16
f =
1/(t^3 + 3*t^2 + 5*t - 9)^6
der6 =
-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)Octave esegue il codice e restituisce il seguente risultato:
f =
(2.0+x)*(3.0+x^(2.0))
der1 =
3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =
(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =
(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =
(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =
(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =
(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =
(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =
(1.0+x^(2.0))^(17.0)
der5 =
(34.0)*(1.0+x^(2.0))^(16.0)*x
f =
(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =
-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)Derivate di funzioni esponenziali, logaritmiche e trigonometriche
La tabella seguente fornisce i derivati delle funzioni esponenziali, logaritmiche e trigonometriche di uso comune:
| Funzione | Derivato |
|---|---|
| ca.x | c a.x .ln ca (ln è il logaritmo naturale) |
| ex | e x |
| ln x | 1 / x |
| lncx | 1 / x.ln c |
| xx | x x . (1 + ln x) |
| sin(x) | cos (x) |
| cos(x) | -sin (x) |
| tan(x) | sec 2 (x) o 1 / cos 2 (x) o 1 + tan 2 (x) |
| cot(x) | -csc 2 (x), o -1 / sin 2 (x) o - (1 + cot 2 (x)) |
| sec(x) | sec (x) .tan (x) |
| csc(x) | -csc (x) .cot (x) |
Esempio
Crea un file di script e digita il seguente codice al suo interno:
syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)Quando esegui il file, MATLAB mostra il seguente risultato:
y =
exp(x)
ans =
exp(x)
y =
x^9
ans =
9*x^8
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
tan(x)^2 + 1
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
1/x
y =
log(x)/log(10)
ans =
1/(x*log(10))
y =
sin(x)^2
ans =
2*cos(x)*sin(x)
y =
cos(3*x^2 + 2*x + 1)
ans =
-sin(3*x^2 + 2*x + 1)*(6*x + 2)
y =
exp(x)/sin(x)
ans =
exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)Octave esegue il codice e restituisce il seguente risultato:
y =
exp(x)
ans =
exp(x)
y =
x^(9.0)
ans =
(9.0)*x^(8.0)
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
1+tan(x)^2
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
x^(-1)
y =
sin(x)^(2.0)
ans =
(2.0)*sin(x)*cos(x)
y =
cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =
-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =
sin(x)^(-1)*exp(x)
ans =
sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)Calcolo di derivati di ordine superiore
Per calcolare derivate superiori di una funzione f, usiamo la sintassi diff(f,n).
Calcoliamo la derivata seconda della funzione y = f (x) = x. E -3x
f = x*exp(-3*x);
diff(f, 2)MATLAB esegue il codice e restituisce il seguente risultato:
ans =
9*x*exp(-3*x) - 6*exp(-3*x)Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)Octave esegue il codice e restituisce il seguente risultato:
ans =
(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)Esempio
In questo esempio, risolviamo un problema. Dato che una funzioney = f(x) = 3 sin(x) + 7 cos(5x). Dovremo scoprire se l'equazionef" + f = -5cos(2x) è vero.
Crea un file di script e digita il seguente codice al suo interno:
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);Quando si esegue il file, viene visualizzato il seguente risultato:
No, the equation does not hold true
Value of LHS is:
-168*cos(5*x)Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);Octave esegue il codice e restituisce il seguente risultato:
No, the equation does not hold true
Value of LHS is:
-(168.0)*cos((5.0)*x)Trovare i massimi e i minimi di una curva
Se stiamo cercando i massimi e minimi locali per un grafico, stiamo fondamentalmente cercando i punti più alti o più bassi sul grafico della funzione in una particolare località, o per un particolare intervallo di valori della variabile simbolica.
Per una funzione y = f (x) vengono chiamati i punti del grafico in cui il grafico ha pendenza zero stationary points. In altre parole, i punti stazionari sono dove f '(x) = 0.
Per trovare i punti stazionari di una funzione che differenziamo, dobbiamo impostare la derivata uguale a zero e risolvere l'equazione.
Esempio
Troviamo i punti stazionari della funzione f (x) = 2x 3 + 3x 2 - 12x + 17
Procedi nel seguente modo:
First let us enter the function and plot its graph.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y)MATLAB esegue il codice e restituisce la seguente trama:
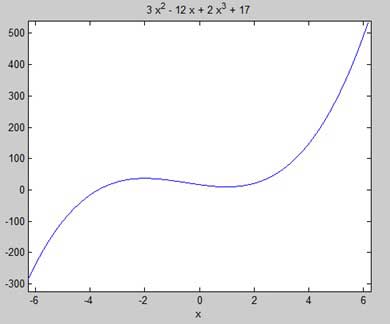
Ecco il codice equivalente a Octave per l'esempio precedente:
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.epsOur aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y, [-2, 2])MATLAB esegue il codice e restituisce la seguente trama:
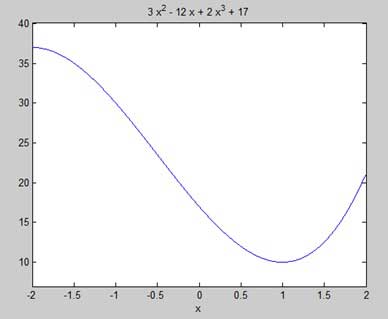
Ecco il codice equivalente a Octave per l'esempio precedente:
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.epsNext, let us compute the derivative.
g = diff(y)MATLAB esegue il codice e restituisce il seguente risultato:
g =
6*x^2 + 6*x - 12Ecco l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)Octave esegue il codice e restituisce il seguente risultato:
g =
-12.0+(6.0)*x+(6.0)*x^(2.0)Let us solve the derivative function, g, to get the values where it becomes zero.
s = solve(g)MATLAB esegue il codice e restituisce il seguente risultato:
s =
1
-2Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])Octave esegue il codice e restituisce il seguente risultato:
g =
-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =
-2
1This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Possiamo sostituire un valore in una funzione simbolica usando il subs comando.
subs(y, 1), subs(y, -2)MATLAB esegue il codice e restituisce il seguente risultato:
ans =
10
ans =
37Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)ans =
10.0
ans =
37.0-4.6734207789940138748E-18*IPertanto, i valori minimo e massimo sulla funzione f (x) = 2x 3 + 3x 2 - 12x + 17, nell'intervallo [-2,2] sono 10 e 37.
Risoluzione di equazioni differenziali
MATLAB fornisce il dsolve comando per risolvere simbolicamente equazioni differenziali.
La forma più semplice di dsolve comando per trovare la soluzione a una singola equazione è
dsolve('eqn')dove eqn è una stringa di testo utilizzata per inserire l'equazione.
Restituisce una soluzione simbolica con un insieme di costanti arbitrarie che MATLAB etichetta C1, C2 e così via.
È inoltre possibile specificare le condizioni iniziali e al contorno per il problema, come elenco delimitato da virgole che segue l'equazione come -
dsolve('eqn','cond1', 'cond2',…)Allo scopo di utilizzare il comando dsolve, derivatives are indicated with a D. Ad esempio, un'equazione come f '(t) = -2 * f + cost (t) viene inserita come -
'Df = -2*f + cos(t)'
I derivati superiori sono indicati seguendo la D nell'ordine del derivato.
Ad esempio, l'equazione f "(x) + 2f '(x) = 5sin3x deve essere inserita come -
'D2y + 2Dy = 5*sin(3*x)'
Prendiamo un semplice esempio di un'equazione differenziale del primo ordine: y '= 5y.
s = dsolve('Dy = 5*y')MATLAB esegue il codice e restituisce il seguente risultato:
s =
C2*exp(5*t)Prendiamo un altro esempio di equazione differenziale del secondo ordine come: y "- y = 0, y (0) = -1, y '(0) = 2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')MATLAB esegue il codice e restituisce il seguente risultato:
ans =
exp(t)/2 - (3*exp(-t))/2L'integrazione si occupa di due tipi di problemi essenzialmente diversi.
Nel primo tipo, viene data la derivata di una funzione e vogliamo trovare la funzione. Pertanto, sostanzialmente invertiamo il processo di differenziazione. Questo processo inverso è noto come anti-differenziazione, o trovare la funzione primitiva o trovare un fileindefinite integral.
Il secondo tipo di problemi consiste nel sommare un numero molto grande di quantità molto piccole e quindi prendere un limite quando la dimensione delle quantità si avvicina allo zero, mentre il numero dei termini tende all'infinito. Questo processo porta alla definizione didefinite integral.
Gli integrali definiti vengono utilizzati per trovare area, volume, baricentro, momento di inerzia, lavoro svolto da una forza e in numerose altre applicazioni.
Trovare l'integrale indefinito utilizzando MATLAB
Per definizione, se la derivata di una funzione f (x) è f '(x), allora diciamo che un integrale indefinito di f' (x) rispetto a x è f (x). Ad esempio, poiché la derivata (rispetto a x) di x 2 è 2x, possiamo dire che un integrale indefinito di 2x è x 2 .
In simboli -
f'(x2) = 2x, perciò,
∫ 2xdx = x2.
L'integrale indefinito non è univoco, perché anche la derivata di x 2 + c, per qualsiasi valore di una costante c, sarà 2x.
Questo è espresso in simboli come -
∫ 2xdx = x2 + c.
Dove, c è chiamata "costante arbitraria".
MATLAB fornisce un file intcomando per il calcolo dell'integrale di un'espressione. Per derivare un'espressione per l'integrale indefinito di una funzione, scriviamo -
int(f);Ad esempio, dal nostro esempio precedente:
syms x
int(2*x)MATLAB esegue l'istruzione di cui sopra e restituisce il seguente risultato:
ans =
x^2Esempio 1
In questo esempio, troviamo l'integrale di alcune espressioni di uso comune. Crea un file di script e digita il seguente codice al suo interno:
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)Quando si esegue il file, viene visualizzato il seguente risultato:
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)Esempio 2
Crea un file di script e digita il seguente codice al suo interno:
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))Nota che il file pretty restituisce un'espressione in un formato più leggibile.
Quando si esegue il file, viene visualizzato il seguente risultato:
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2Trovare un integrale definito usando MATLAB
Per definizione, l'integrale definito è fondamentalmente il limite di una somma. Usiamo integrali definiti per trovare aree come l'area tra una curva e l'asse x e l'area tra due curve. Gli integrali definiti possono essere utilizzati anche in altre situazioni, dove la quantità richiesta può essere espressa come limite di una somma.
Il int la funzione può essere utilizzata per un'integrazione definita passando i limiti oltre i quali si vuole calcolare l'integrale.
Calcolare
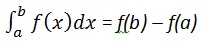
scriviamo,
int(x, a, b)Ad esempio, per calcolare il valore di

int(x, 4, 9)MATLAB esegue l'istruzione di cui sopra e restituisce il seguente risultato:
ans =
65/2Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));Octave esegue il codice e restituisce il seguente risultato:
Area:
32.500Una soluzione alternativa può essere fornita usando la funzione quad () fornita da Octave come segue:
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));Octave esegue il codice e restituisce il seguente risultato:
Area:
32.500Esempio 1
Calcoliamo l'area racchiusa tra l'asse xe la curva y = x 3 −2x + 5 e le ordinate x = 1 ex = 2.
L'area richiesta è data da:
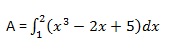
Crea un file di script e digita il codice seguente:
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));Quando si esegue il file, viene visualizzato il seguente risultato:
a =
23/4
Area:
5.7500Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));Octave esegue il codice e restituisce il seguente risultato:
Area:
5.7500Una soluzione alternativa può essere fornita usando la funzione quad () fornita da Octave come segue:
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));Octave esegue il codice e restituisce il seguente risultato:
Area:
5.7500Esempio 2
Trova l'area sotto la curva: f (x) = x 2 cos (x) per −4 ≤ x ≤ 9.
Crea un file di script e scrivi il codice seguente:
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Quando esegui il file, MATLAB traccia il grafico:
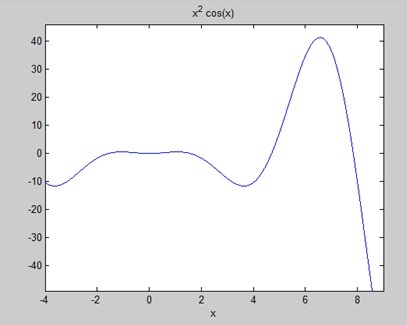
L'output è fornito di seguito:
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326Di seguito è riportato l'equivalente in ottava del calcolo precedente:
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));MATLAB rappresenta i polinomi come vettori riga contenenti coefficienti ordinati per potenze discendenti. Ad esempio, l'equazione P (x) = x 4 + 7x 3 - 5x + 9 potrebbe essere rappresentata come -
p = [1 7 0 -5 9];
Valutazione dei polinomi
Il polyvalviene utilizzata per valutare un polinomio a un valore specificato. Ad esempio, per valutare il nostro polinomio precedentep, in x = 4, digitare -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB esegue le istruzioni precedenti e restituisce il seguente risultato:
ans = 693MATLAB fornisce anche il polyvalmfunzione per valutare un polinomio di matrice. Un polinomio di matrice è unpolynomial con matrici come variabili.
Ad esempio, creiamo una matrice quadrata X e valutiamo il polinomio p, in X -
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB esegue le istruzioni precedenti e restituisce il seguente risultato:
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269Trovare le radici dei polinomi
Il rootsfunzione calcola le radici di un polinomio. Ad esempio, per calcolare le radici del nostro polinomio p, digita -
p = [1 7 0 -5 9];
r = roots(p)MATLAB esegue le istruzioni precedenti e restituisce il seguente risultato:
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095iLa funzione polyè un inverso della funzione radici e ritorna ai coefficienti polinomiali. Ad esempio:
p2 = poly(r)MATLAB esegue le istruzioni precedenti e restituisce il seguente risultato:
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000iAdattamento della curva polinomiale
Il polyfittrova i coefficienti di un polinomio che si adatta a un insieme di dati nel senso dei minimi quadrati. Se xey sono due vettori contenenti i dati xey da adattare a un polinomio di n gradi, allora otteniamo il polinomio che si adatta ai dati scrivendo -
p = polyfit(x,y,n)Esempio
Crea un file di script e digita il codice seguente:
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid onQuando esegui il file, MATLAB mostra il seguente risultato:
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250E traccia il grafico seguente:
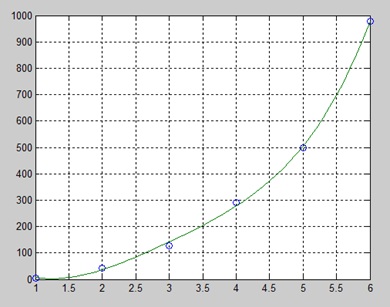
MATLAB fornisce il comando per lavorare con le trasformazioni, come le trasformate di Laplace e Fourier. Le trasformazioni sono utilizzate nella scienza e nell'ingegneria come strumento per semplificare l'analisi e guardare i dati da un'altra angolazione.
Ad esempio, la trasformata di Fourier ci permette di convertire un segnale rappresentato in funzione del tempo in una funzione di frequenza. La trasformata di Laplace ci consente di convertire un'equazione differenziale in un'equazione algebrica.
MATLAB fornisce il laplace, fourier e fft comandi per lavorare con trasformate di Laplace, Fourier e Fast Fourier.
La trasformata di Laplace
La trasformata di Laplace di una funzione del tempo f (t) è data dal seguente integrale -
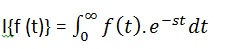
La trasformata di Laplace è anche indicata come trasformata di f (t) in F (s). Puoi vedere che questo processo di trasformazione o integrazione converte f (t), una funzione della variabile simbolica t, in un'altra funzione F (s), con un'altra variabile s.
La trasformata di Laplace trasforma le equazioni differenziali in equazioni algebriche. Per calcolare una trasformata di Laplace di una funzione f (t), scrivi -
laplace(f(t))Esempio
In questo esempio, calcoleremo la trasformata di Laplace di alcune funzioni di uso comune.
Crea un file di script e digita il codice seguente:
syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))Quando si esegue il file, viene visualizzato il seguente risultato:
ans =
1/s^2
ans =
2/s^3
ans =
362880/s^10
ans =
1/(b + s)
ans =
w/(s^2 + w^2)
ans =
s/(s^2 + w^2)Trasformata inversa di Laplace
MATLAB ci permette di calcolare la trasformata inversa di Laplace utilizzando il comando ilaplace.
Per esempio,
ilaplace(1/s^3)MATLAB eseguirà l'istruzione precedente e visualizzerà il risultato -
ans =
t^2/2Esempio
Crea un file di script e digita il codice seguente:
syms s t a b w
ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))Quando si esegue il file, viene visualizzato il seguente risultato:
ans =
t^6/720
ans =
2*exp(-t*w)
ans =
cos(2*t)
ans =
ilaplace(exp(-b*t), t, x)
ans =
sin(t*w)
ans =
cos(t*w)Le trasformate di Fourier
La trasformata di Fourier trasforma comunemente una funzione matematica del tempo, f (t), in una nuova funzione, a volte indicata con o F, il cui argomento è la frequenza con unità di cicli / s (hertz) o radianti al secondo. La nuova funzione è quindi nota come trasformata di Fourier e / o spettro di frequenza della funzione f.
Esempio
Crea un file di script e digita il seguente codice al suo interno:
syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transformQuando esegui il file, MATLAB traccia il grafico seguente:
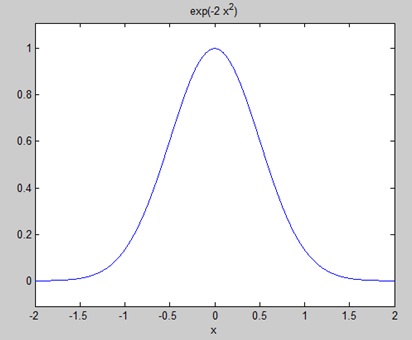
Viene visualizzato il seguente risultato:
FT =
(2^(1/2)*pi^(1/2)*exp(-w^2/8))/2Tracciare la trasformata di Fourier come -
ezplot(FT)Fornisce il grafico seguente:

Trasformate di Fourier inverse
MATLAB fornisce il ifouriercomando per calcolare la trasformata di Fourier inversa di una funzione. Per esempio,
f = ifourier(-2*exp(-abs(w)))MATLAB eseguirà l'istruzione precedente e visualizzerà il risultato -
f =
-2/(pi*(x^2 + 1))GNU Octave è un linguaggio di programmazione di alto livello come MATLAB ed è principalmente compatibile con MATLAB. Viene anche utilizzato per calcoli numerici.
Octave ha le seguenti caratteristiche comuni con MATLAB:
- le matrici sono tipi di dati fondamentali
- ha il supporto integrato per i numeri complessi
- ha funzioni matematiche e librerie incorporate
- supporta funzioni definite dall'utente
GNU Octave è anche un software ridistribuibile gratuitamente. È possibile ridistribuirlo e / o modificarlo secondo i termini della GNU General Public License (GPL) come pubblicata dalla Free Software Foundation.
MATLAB vs Octave
La maggior parte dei programmi MATLAB vengono eseguiti in Octave, ma alcuni programmi Octave potrebbero non funzionare in MATLAB perché Octave consente una sintassi che MATLAB non consente.
Ad esempio, MATLAB supporta solo virgolette singole, ma Octave supporta virgolette singole e doppie per la definizione delle stringhe. Se stai cercando un tutorial su Octave, segui gentilmente questo tutorial dall'inizio che copre sia MATLAB che Octave.
Esempi compatibili
Quasi tutti gli esempi trattati in questo tutorial sono compatibili con MATLAB e con Octave. Proviamo a seguire l'esempio in MATLAB e Octave che produce lo stesso risultato senza modifiche alla sintassi -
Questo esempio crea una mappa della superficie 3D per la funzione g = xe - (x 2 + y 2 ) . Crea un file di script e digita il codice seguente:
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.epsQuando esegui il file, MATLAB mostra la seguente mappa 3-D:

Esempi non compatibili
Sebbene tutte le funzionalità principali di MATLAB siano disponibili in Octave, esistono alcune funzionalità, ad esempio, Calcolo differenziale e integrazione, che non corrispondono esattamente in entrambe le lingue. Questo tutorial ha cercato di fornire entrambi i tipi di esempi in cui differivano nella loro sintassi.
Considera il seguente esempio in cui MATLAB e Octave fanno uso di funzioni diverse per ottenere l'area di una curva: f (x) = x 2 cos (x) per −4 ≤ x ≤ 9. Di seguito è riportata la versione MATLAB del codice:
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Quando esegui il file, MATLAB traccia il grafico:

Viene visualizzato il seguente risultato
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326Ma per dare un'area della stessa curva in Octave, dovrai farne uso symbolic pacchetto come segue -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));Simulink è un ambiente di simulazione e di progettazione basato su modelli per sistemi dinamici e integrati, integrato con MATLAB. Simulink, sviluppato anche da MathWorks, è uno strumento di linguaggio di programmazione grafico per flussi di dati per modellare, simulare e analizzare sistemi dinamici multi-dominio. È fondamentalmente uno strumento grafico per la creazione di diagrammi a blocchi con un set personalizzabile di librerie di blocchi.
Ti consente di incorporare algoritmi MATLAB nei modelli e di esportare i risultati della simulazione in MATLAB per ulteriori analisi.
Simulink supporta:
- progettazione a livello di sistema
- simulation
- generazione automatica del codice
- test e verifica di sistemi embedded
Esistono molti altri prodotti aggiuntivi forniti da MathWorks e prodotti hardware e software di terze parti disponibili per l'uso con Simulink.
Il seguente elenco fornisce una breve descrizione di alcuni di essi:
Stateflow consente di sviluppare macchine a stati e diagrammi di flusso.
Simulink Coder consente la generazione di codice sorgente C per l'implementazione automatica dei sistemi in tempo reale.
xPC Target insieme a x86-based real-time systems fornire un ambiente per simulare e testare i modelli Simulink e Stateflow in tempo reale sul sistema fisico.
Embedded Coder supporta target specifici incorporati.
HDL Coder permette di generare automaticamente VHDL e Verilog sintetizzabili.
SimEvents fornisce una libreria di blocchi grafici per la modellazione di sistemi di accodamento.
Simulink è in grado di verificare e convalidare sistematicamente i modelli attraverso il controllo dello stile di modellazione, la tracciabilità dei requisiti e l'analisi della copertura del modello.
Simulink Design Verifier ti consente di identificare gli errori di progettazione e di generare scenari di test case per il controllo del modello.
Utilizzando Simulink
Per aprire Simulink, digita nello spazio di lavoro MATLAB -
simulinkSimulink si apre con il Library Browser. Il browser della libreria viene utilizzato per creare modelli di simulazione.

Nel riquadro della finestra di sinistra, troverai diverse librerie classificate in base a vari sistemi, facendo clic su ciascuna di esse verranno visualizzati i blocchi di progettazione nel riquadro della finestra di destra.
Modelli di costruzione
Per creare un nuovo modello, fare clic su Newsulla barra degli strumenti del browser della libreria. Si apre una nuova finestra del modello senza titolo.
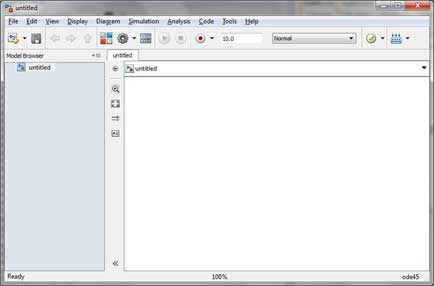
Un modello Simulink è uno schema a blocchi.
Gli elementi del modello vengono aggiunti selezionando gli elementi appropriati dal browser della libreria e trascinandoli nella finestra del modello.
In alternativa, è possibile copiare gli elementi del modello e incollarli nella finestra del modello.
Esempi
Trascina e rilascia elementi dalla libreria Simulink per creare il tuo progetto.
Ai fini di questo esempio, verranno utilizzati due blocchi per la simulazione: A Source (un segnale) e a Sink(un ambito). Un generatore di segnale (la sorgente) genera un segnale analogico, che verrà quindi visualizzato graficamente dall'oscilloscopio (il sink).
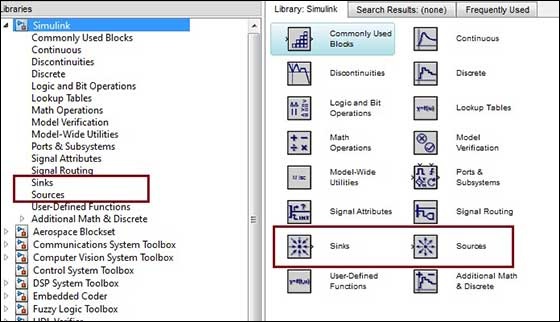
Inizia trascinando i blocchi richiesti dalla libreria alla finestra del progetto. Quindi, collega i blocchi insieme, cosa che può essere eseguita trascinando i connettori dai punti di connessione su un blocco a quelli di un altro.
Trasciniamo un blocco "Sine Wave" nel modello.
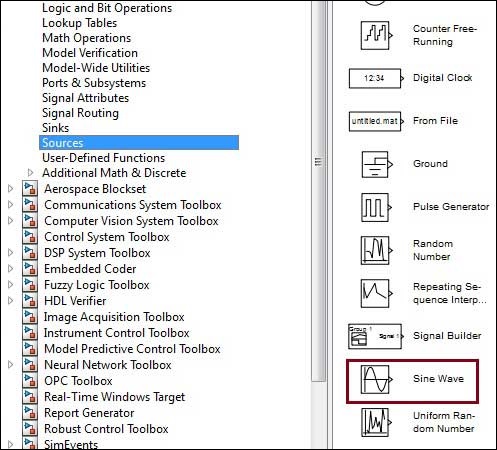
Seleziona "Sinks" dalla libreria e trascina un blocco "Scope" nel modello.
Trascina una linea di segnale dall'uscita del blocco Sine Wave all'ingresso del blocco Scope.
Eseguire la simulazione premendo il tasto 'Run'pulsante, mantenendo tutti i parametri predefiniti (puoi modificarli dal menu Simulazione)
Dovresti ottenere il grafico sottostante dall'ambito.