R - Minimo quadrato non lineare
Quando si modellano i dati del mondo reale per l'analisi di regressione, si osserva che è raro che l'equazione del modello sia un'equazione lineare che fornisce un grafico lineare. Il più delle volte, l'equazione del modello dei dati del mondo reale coinvolge funzioni matematiche di grado più elevato come un esponente di 3 o una funzione sin. In un tale scenario, il grafico del modello fornisce una curva piuttosto che una linea. L'obiettivo della regressione lineare e non lineare è regolare i valori dei parametri del modello per trovare la linea o la curva che si avvicina di più ai dati. Trovando questi valori saremo in grado di stimare la variabile di risposta con buona precisione.
Nella regressione dei minimi quadrati, stabiliamo un modello di regressione in cui la somma dei quadrati delle distanze verticali di diversi punti dalla curva di regressione è ridotta al minimo. In genere iniziamo con un modello definito e assumiamo alcuni valori per i coefficienti. Quindi applichiamo ilnls() funzione di R per ottenere i valori più accurati insieme agli intervalli di confidenza.
Sintassi
La sintassi di base per creare un test dei minimi quadrati non lineare in R è:
nls(formula, data, start)Di seguito la descrizione dei parametri utilizzati:
formula è una formula del modello non lineare che include variabili e parametri.
data è un data frame utilizzato per valutare le variabili nella formula.
start è una lista con nome o un vettore numerico con nome di stime iniziali.
Esempio
Considereremo un modello non lineare con l'assunzione dei valori iniziali dei suoi coefficienti. Successivamente vedremo quali sono gli intervalli di confidenza di questi valori presunti in modo da poter giudicare quanto bene questi valori siano inseriti nel modello.
Quindi consideriamo l'equazione seguente per questo scopo:
a = b1*x^2+b2Supponiamo che i coefficienti iniziali siano 1 e 3 e adattiamo questi valori alla funzione nls ().
xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
# Give the chart file a name.
png(file = "nls.png")
# Plot these values.
plot(xvalues,yvalues)
# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))
# Save the file.
dev.off()
# Get the sum of the squared residuals.
print(sum(resid(model)^2))
# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))Quando eseguiamo il codice sopra, produce il seguente risultato:
[1] 1.081935
Waiting for profiling to be done...
2.5% 97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484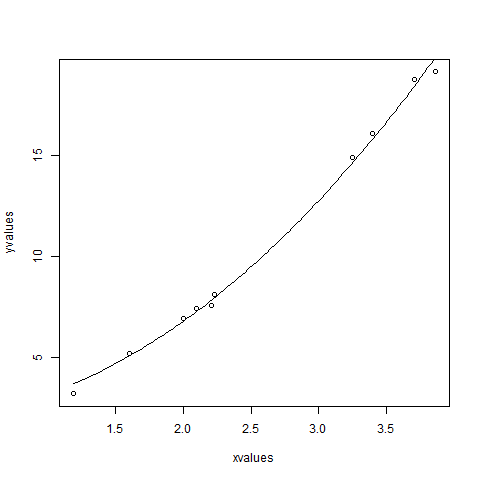
Possiamo concludere che il valore di b1 è più vicino a 1 mentre il valore di b2 è più vicino a 2 e non a 3.