SymPy - Guida rapida

SymPy è una libreria Python per eseguire calcoli simbolici. È uncomputer algebra system(CAS) che può essere utilizzato sia come applicazione standalone, sia come libreria per altre applicazioni. La sua sessione live è disponibile anche suhttps://live.sympy.org/. Poiché è una libreria Python pura, può essere utilizzata come modalità interattiva e come applicazione programmatica. SymPy è ora diventata una popolare libreria simbolica per l'ecosistema scientifico Python.

SymPy ha un'ampia gamma di funzionalità applicabili nel campo dell'aritmetica simbolica di base, calcolo, algebra, matematica discreta, fisica quantistica, ecc. SymPy è in grado di formattare i risultati in una varietà di formati tra cui LaTeX, MathML, ecc. SymPy è distribuito sotto Nuova licenza BSD. Un team di sviluppatori guidato daOndřej Čertík e Aaron Meurer ha pubblicato la prima versione di SymPy nel 2007. La sua versione attuale è 1.5.1.

Alcune delle aree di applicazione di SymPy sono:

Polynomials
Calculus
Matematica discreta
Matrices
Geometry
Plotting
Physics
Statistics
Combinatorics

SymPy ha un'importante libreria di prerequisiti denominata mpmath. È una libreria Python per aritmetica in virgola mobile reale e complessa con precisione arbitraria. Tuttavia, il programma di installazione del pacchetto di Python PIP lo installa automaticamente quando SymPy viene installato come segue:

pip install sympy

Altre distribuzioni Python come Anaconda, En Thought Canopy, ecc., Potrebbero avere SymPy già in bundle. Per verificare, puoi digitare quanto segue nel prompt di Python:

>>> import sympy
>>> sympy.__version__

E ottieni l'output di seguito come la versione corrente di sympy -

'1.5.1'

Il codice sorgente del pacchetto SymPy è disponibile all'indirizzo https://github.com/sympy/sympy.

Il calcolo simbolico si riferisce allo sviluppo di algoritmi per la manipolazione di espressioni matematiche e altri oggetti matematici. Il calcolo simbolico integra la matematica con l'informatica per risolvere espressioni matematiche utilizzando simboli matematici. Un Computer Algebra System (CAS) come SymPy valuta le espressioni algebriche esattamente (non approssimativamente) utilizzando gli stessi simboli utilizzati nel metodo manuale tradizionale. Ad esempio, calcoliamo la radice quadrata di un numero utilizzando il modulo matematico di Python come indicato di seguito:

>>> import math 
>>> print (math.sqrt(25), math.sqrt(7))

L'output per lo snippet di codice sopra è il seguente:

5.0 2.6457513110645907

Come puoi vedere, la radice quadrata di 7 viene calcolata approssimativamente. Ma in SymPy le radici quadrate dei numeri che non sono quadrati perfetti vengono lasciati non valutati per impostazione predefinita come indicato di seguito:

>>> import sympy 
>>> print (sympy.sqrt(7))

L'output per lo snippet di codice sopra è il seguente:

sqrt(7)

È possibile semplificare e mostrare il risultato dell'espressione simbolicamente con lo snippet di codice seguente:

>>> import math
>>> print (math.sqrt(12))

L'output per lo snippet di codice sopra è il seguente:

3.4641016151377544

È necessario utilizzare lo snippet di codice seguente per eseguire lo stesso utilizzando sympy -

##sympy output 
>>> print (sympy.sqrt(12))

E l'output per questo è il seguente:

2*sqrt(3)

Il codice SymPy, quando viene eseguito nel notebook Jupyter, utilizza la libreria MathJax per eseguire il rendering dei simboli matematici in formato LatEx. Viene mostrato nello snippet di codice seguente:

>>> from sympy import * 
>>> x=Symbol ('x') 
>>> expr = integrate(x**x, x) 
>>> expr

Eseguendo il comando precedente nella shell python, verrà generato il seguente output:

Integral(x**x, x)

Che è equivalente a

$\int \mathrm{x}^{x}\,\mathrm{d}x$

La radice quadrata di un quadrato non perfetto può essere rappresentata da Latex come segue utilizzando il simbolo tradizionale:

>>> from sympy import * 
>>> x=7 
>>> sqrt(x)

L'output per lo snippet di codice sopra è il seguente:

$\sqrt7$

Un sistema di calcolo simbolico come SymPy esegue tutti i tipi di calcoli (come derivate, integrali e limiti, risolve equazioni, lavora con matrici) simbolicamente. Il pacchetto SymPy ha diversi moduli che supportano il plottaggio, la stampa (come LATEX), la fisica, la statistica, la combinatoria, la teoria dei numeri, la geometria, la logica, ecc.

Il modulo principale nel pacchetto SymPy contiene la classe Number che rappresenta i numeri atomici. Questa classe ha due sottoclassi: Float e Rational class. La classe razionale è ulteriormente estesa dalla classe Integer.

La classe Float rappresenta un numero in virgola mobile di precisione arbitraria.

>>> from sympy import Float 
>>> Float(6.32)

L'output per lo snippet di codice sopra è il seguente:

6.32

SymPy può convertire un numero intero o una stringa in float.

>>> Float(10)

10.0

Float('1.33E5')# scientific notation

133000.0

Durante la conversione in float, è anche possibile specificare il numero di cifre per la precisione come indicato di seguito:

>>> Float(1.33333,2)

L'output per lo snippet di codice sopra è il seguente:

1.3

Una rappresentazione di un numero (p / q) è rappresentata come oggetto della classe Rational dove q è un numero diverso da zero.

>>> Rational(3/4)

L'output per lo snippet di codice sopra è il seguente:

$\frac{3}{4}$

Se un numero in virgola mobile viene passato al costruttore Rational (), restituisce il valore sottostante della sua rappresentazione binaria

>>> Rational(0.2)

L'output per lo snippet di codice sopra è il seguente:

$\frac{3602879701896397}{18014398509481984}$

Per una rappresentazione più semplice, specificare la limitazione del denominatore.

>>> Rational(0.2).limit_denominator(100)

L'output per lo snippet di codice sopra è il seguente:

$\frac{1}{5}$

Quando una stringa viene passata al costruttore Rational (), viene restituito un numero razionale di precisione arbitraria.

>>> Rational("3.65")

L'output per lo snippet di codice sopra è il seguente:

$\frac{73}{20}$

L'oggetto razionale può anche essere ottenuto se vengono passati due argomenti numerici. Le parti numeratore e denominatore sono disponibili come proprietà.

>>> a=Rational(3,5) 
>>> print (a) 
>>> print ("numerator:{}, denominator:{}".format(a.p, a.q))

L'output per lo snippet di codice sopra è il seguente:

3/5

numerator:3, denominator:5

>>> a

L'output per lo snippet di codice sopra è il seguente:

$\frac{3}{5}$

La classe Integer in SymPy rappresenta un numero intero di qualsiasi dimensione. Il costruttore può accettare un numero Float o Razionale, ma la parte frazionaria viene scartata

>>> Integer(10)

L'output per lo snippet di codice sopra è il seguente:

>>> Integer(3.4)

L'output per lo snippet di codice sopra è il seguente:

>>> Integer(2/7)

L'output per lo snippet di codice sopra è il seguente:

SymPy ha un file RealNumberclasse che funge da alias per Float. SymPy definisce anche Zero e One come classi singleton accessibili rispettivamente con S.Zero e S.One, come mostrato di seguito -

>>> S.Zero

L'output è il seguente:

>>> S.One

L'output è il seguente:

Altri oggetti numerici Singleton predefiniti sono Half, NaN, Infinity e ImaginaryUnit

>>> from sympy import S 
>>> print (S.Half)

L'output è il seguente:

>>> print (S.NaN)

L'output è il seguente:

nan

Infinity è disponibile come oggetto simbolo oo o S. Infinity

>>> from sympy import oo 
>>> oo

L'output per lo snippet di codice sopra è il seguente:

$\infty$

>>> S.Infinity

L'output per lo snippet di codice sopra è il seguente:

$\infty$

Il numero di ImaginaryUnit può essere importato come simbolo I o accessibile come S.ImaginaryUnit e rappresenta la radice quadrata di -1

>>> from sympy import I 
>>> I

Quando esegui lo snippet di codice sopra, ottieni il seguente output:

>>> S.ImaginaryUnit

L'output dello snippet di cui sopra è il seguente:

>>> from sympy import sqrt 
>>> i=sqrt(-1) 
>>> i*i

Quando esegui lo snippet di codice sopra, ottieni il seguente output:

-1

Symbolè la classe più importante nella libreria symPy. Come accennato in precedenza, i calcoli simbolici vengono eseguiti con i simboli. Le variabili SymPy sono oggetti della classe Symbols.

L'argomento della funzione Symbol () è una stringa contenente un simbolo che può essere assegnato a una variabile.

>>> from sympy import Symbol 
>>> x=Symbol('x') 
>>> y=Symbol('y') 
>>> expr=x**2+y**2 
>>> expr

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$x^2 + y^2$

Un simbolo può essere composto da più alfabeti.

>>> s=Symbol('side') 
>>> s**3

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$side^3$

SymPy ha anche un file Symbols()funzione che può definire più simboli contemporaneamente. La stringa contiene nomi di variabili separati da virgola o spazio.

>>> from sympy import symbols 
>>> x,y,z=symbols("x,y,z")

Nel modulo abc di SymPy, tutti gli alfabeti latini e greci sono definiti come simboli. Quindi, invece di istanziare l'oggetto Symbol, questo metodo è conveniente.

>>> from sympy.abc import x,y,z

Tuttavia, i nomi C, O, S, I, N, E e Qsono simboli predefiniti. Inoltre, i simboli con più di un alfabeto non sono definiti nel modulo abc, per il quale dovresti usare l'oggetto Symbol come sopra. Il modulo abc definisce nomi speciali in grado di rilevare definizioni nello spazio dei nomi SymPy predefinito. clash1 contiene singole lettere e clash2 ha simboli di conflitto tra più lettere

>>> from sympy.abc import _clash1, _clash2 
>>> _clash1

L'output dello snippet di cui sopra è il seguente:

{'C': C, 'O': O, 'Q': Q, 'N': N, 'I': I, 'E': E, 'S': S}

>>> _clash2

L'output dello snippet di cui sopra è il seguente:

{'beta': beta, 'zeta': zeta, 'gamma': gamma, 'pi': pi}

I simboli indicizzati possono essere definiti utilizzando una sintassi simile alla funzione range (). Gli intervalli sono indicati da due punti. Il tipo di intervallo è determinato dal carattere a destra dei due punti. Se itr è una cifra, tutte le cifre contigue a sinistra vengono prese come valore iniziale non negativo. Tutte le cifre contigue a destra vengono prese come 1 maggiore del valore finale.

>>> from sympy import symbols 
>>> symbols('a:5')

L'output dello snippet di cui sopra è il seguente:

(a0, a1, a2, a3, a4)

>>> symbols('mark(1:4)')

L'output dello snippet di cui sopra è il seguente:

(mark1, mark2, mark3)

Una delle operazioni più basilari da eseguire su un'espressione matematica è la sostituzione. La funzione subs () in SymPy sostituisce tutte le occorrenze del primo parametro con il secondo.

>>> from sympy.abc import x,a 
>>> expr=sin(x)*sin(x)+cos(x)*cos(x) 
>>> expr

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$\sin^2(x)+\cos^2(x)$

>>> expr.subs(x,a)

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$\sin^2(a)+\cos^2(a)$

Questa funzione è utile se vogliamo valutare una certa espressione. Ad esempio, vogliamo calcolare i valori della seguente espressione sostituendo a con 5.

>>> expr=a*a+2*a+5 
>>> expr

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$a^2 + 2a + 5$

expr.subs(a,5)

Lo snippet di codice sopra fornisce il seguente output:

>>> from sympy.abc import x 
>>> from sympy import sin, pi 
>>> expr=sin(x) 
>>> expr1=expr.subs(x,pi) 
>>> expr1

Lo snippet di codice sopra fornisce il seguente output:

Questa funzione viene utilizzata anche per sostituire una sottoespressione con un'altra sottoespressione. Nell'esempio seguente, b è sostituito da a + b.

>>> from sympy.abc import a,b 
>>> expr=(a+b)**2 
>>> expr1=expr.subs(b,a+b) 
>>> expr1

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$(2a + b)^2$

La funzione sympify () viene utilizzata per convertire qualsiasi espressione arbitraria in modo che possa essere utilizzata come espressione SymPy. I normali oggetti Python come gli oggetti interi vengono convertiti in SymPy. Intero, ecc., Anche le stringhe vengono convertite in espressioni SymPy.

>>> expr="x**2+3*x+2" 
>>> expr1=sympify(expr) 
>>> expr1 
>>> expr1.subs(x,2)

Lo snippet di codice sopra fornisce il seguente output:

Qualsiasi oggetto Python può essere convertito in un oggetto SymPy. Tuttavia, poiché la conversione utilizza internamente la funzione eval (), l'espressione non disinfettata non dovrebbe essere utilizzata, altrimenti viene sollevato SympifyError.

>>> sympify("x***2")
---------------------------------------------------------------------------

SympifyError: Sympify of expression 'could not parse' x *** 2 '' non riuscita, a causa dell'eccezione sollevata.

La funzione sympify () accetta i seguenti argomenti: * strict: il valore predefinito è False. Se impostato su True, vengono convertiti solo i tipi per i quali è stata definita una conversione esplicita. Altrimenti, viene sollevato SympifyError. * Valuta: se impostato su False, l'aritmetica e gli operatori verranno convertiti nei loro equivalenti SymPy senza valutare l'espressione.

>>> sympify("10/5+4/2")

Lo snippet di codice sopra fornisce il seguente output:

>>> sympify("10/5+4/2", evaluate=False)

Lo snippet di codice sopra fornisce il seguente output:

$\frac{10}{5}+\frac{4}{2}$

Questa funzione valuta una data espressione numerica fino a una data precisione in virgola mobile fino a 100 cifre. La funzione accetta anche il parametro subs, un oggetto dizionario di valori numerici per i simboli. Considera la seguente espressione

>>> from sympy.abc import r 
>>> expr=pi*r**2 
>>> expr

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$\Pi{r^2}$

Per valutare l'espressione sopra usando la funzione evalf () sostituendo r con 5

>>> expr.evalf(subs={r:5})

Lo snippet di codice sopra fornisce il seguente output:

78.5398163397448

Per impostazione predefinita, la precisione in virgola mobile è fino a 15 cifre che possono essere sovrascritte da qualsiasi numero fino a 100. L'espressione successiva viene valutata fino a 20 cifre di precisione.

>>> expr=a/b 
>>> expr.evalf(20, subs={a:100, b:3})

Lo snippet di codice sopra fornisce il seguente output:

33.333333333333333333

La funzione lambdify traduce le espressioni SymPy in funzioni Python. Se un'espressione deve essere valutata su un ampio intervallo di valori, la funzione evalf () non è efficiente. lambdify si comporta come una funzione lambda, tranne per il fatto che converte i nomi SymPy nei nomi della libreria numerica data, solitamente NumPy. Per impostazione predefinita, lambdify sulle implementazioni nella libreria standard di matematica.

>>> expr=1/sin(x) 
>>> f=lambdify(x, expr) 
>>> f(3.14)

Lo snippet di codice sopra fornisce il seguente output:

627.8831939138764

L'espressione potrebbe avere più di una variabile. In tal caso, il primo argomento della funzione lambdify () è un elenco di variabili, seguito dall'espressione da valutare.

>>> expr=a**2+b**2 
>>> f=lambdify([a,b],expr) 
>>> f(2,3)

Lo snippet di codice sopra fornisce il seguente output:

Tuttavia, per sfruttare la libreria numpy come backend numerico, dobbiamo definire lo stesso come argomento per la funzione lambdify ().

>>> f=lambdify([a,b],expr, "numpy")

Usiamo due array numpy per due argomenti aeb nella funzione sopra. Il tempo di esecuzione è notevolmente veloce in caso di array numpy.

>>> import numpy 
>>> l1=numpy.arange(1,6) 
>>> l2=numpy.arange(6,11) 
>>> f(l1,l2)

Lo snippet di codice sopra fornisce il seguente output:

array([ 37, 53, 73, 97, 125], dtype=int32)

Le funzioni booleane sono definite in sympy.basic.booleanarg module. È possibile costruire espressioni booleane con gli operatori python standard & (And), | (Or), ~ (Not) così come con >> e <<. Le espressioni booleane ereditano dalla classe Basic definita nel modulo principale di SymPy.

Funzione BooleanTrue

Questa funzione è equivalente a True come nel core Python. Restituisce un singleton che può essere recuperato da S.true.

>>> from sympy import * 
>>> x=sympify(true) 
>>> x, S.true

Lo snippet di codice sopra fornisce il seguente output:

(Vero vero)

Funzione BooleanFalse

Allo stesso modo, questa funzione è equivalente a Boolean False in Python ed è accessibile da S.false

>>> from sympy import * 
>>> x=sympify(false) 
>>> x, S.false

Lo snippet di codice sopra fornisce il seguente output:

(Falso, Falso)

E funzione

Una funzione AND logica valuta i suoi due argomenti e restituisce False se uno dei due è False. La funzione emula & operator.

>>> from sympy import * 
>>> from sympy.logic.boolalg import And 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=True 
>>> And(x,y), x"&"y

Lo snippet di codice sopra fornisce il seguente output:

(Vero vero)

>>> y=False 
>>> And(x,y), x"&"y

Lo snippet di codice sopra fornisce il seguente output:

(Falso, Falso)

O funzione

Questa funzione valuta due argomenti booleani e restituisce True se uno dei due è True. Il | l'operatore ne emula convenientemente il comportamento.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Or(x,y), x|y

Lo snippet di codice sopra fornisce il seguente output:

(Vero vero)

>>> x=False 
>>> y=False 
>>> Or(x,y), x|y

Lo snippet di codice sopra fornisce il seguente output:

(Falso, Falso)

Non funziona

Una funzione Logical Not comporta la negazione dell'argomento booleano. Restituisce True se il suo argomento è False e restituisce False se True. L'operatore ~ esegue l'operazione simile alla funzione Non. È mostrato nell'esempio seguente:

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or, And, Not 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Not(x), Not(y)

The above code snippet gives the following output −

(False, True)

>>> Not(And(x,y)), Not(Or(x,y))

The above code snippet gives the following output −

(True, False)

Xor Function

The Logical XOR (exclusive OR) function returns True if an odd number of the arguments are True and the rest are False and returns False if an even number of the arguments are True and the rest are False. Similar operation is performed by ^ operator.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Xor 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False

>>> Xor(x,y), x^y

The above code snippet gives the following output −

(True, True)

>>> a,b,c,d,e=symbols('a b c d e') 
>>> a,b,c,d,e=(True, False, True, True, False) 
>>> Xor(a,b,c,d,e)

The above code snippet gives the following output −

True

In above case, three (odd number) arguments are True, hence Xor returns true. However, if number of True arguments is even, it results in False, as shown below −

>>> a,b,c,d,e=(True, False, False, True, False) 
>>> Xor(a,b,c,d,e)

The above code snippet gives the following output −

False

Nand Function

This function performs Logical NAND operation. It evaluates its arguments and returns True if any of them are False, and False if they are all True.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nand 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nand(a,b,c), Nand(a,c)

The above code snippet gives the following output −

(True, False)

Nor Function

This function performs Logical NOR operation. It evaluates its arguments and returns False if any of them are True, and True if they are all False.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nor 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nor(a,b,c), Nor(a,c)

The above code snippet gives the following output −

(False, False)

Note that even though SymPy provides ^ operator for Xor, ~ for Not, | for Or and & for And functions as convenience, their normal use in Python is as bitwise operators. Hence, if operands are integers, results would be different.

Equivalent function

This function returns equivalence relation. Equivalent(A, B) is True if and only if A and B are both True or both False. The function returns True if all of the arguments are logically equivalent. Returns False otherwise.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Equivalent 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Equivalent(a,b), Equivalent(a,c)

The above code snippet gives the following output −

(False, True)

ITE function

This function acts as If then else clause in a programming language.ITE(A, B, C) evaluates and returns the result of B if A is true else it returns the result of C. All args must be Booleans.

>>> from sympy import * >>> from sympy.logic.boolalg import ITE >>> a,b,c=symbols('a b c') >>> a,b,c=(True, False, True) 
>>> ITE(a,b,c), ITE(a,c,b)

The above code snippet gives the following output −

(False, True)

The assumptions module in SymPy package contains tools for extracting information about expressions. The module defines ask() function for this purpose.

sympy.assumptions.ask(property)

Following properties provide useful information about an expression −

algebraic(x)

To be algebraic, a number must be a root of a non-zero polynomial equation with rational coefficients. √2 because √2 is a solution to x2 − 2 = 0, so it is algebraic.

complex(x)

Complex number predicate. It is true if and only if x belongs to the set of complex numbers.

composite(x)

Composite number predicate returned by ask(Q.composite(x)) is true if and only if x is a positive integer and has at least one positive divisor other than 1 and the number itself.

even, odd

The ask() returns true of x is in the set of even numbers and set of odd numbers respectively.

imaginary

This property represents Imaginary number predicate. It is true if x can be written as a real number multiplied by the imaginary unit I.

integer

This property returned by Q.integer(x) returns true of x belong to set of even numbers.

rational, irrational

Q.irrational(x) is true if and only if x is any real number that cannot be expressed as a ratio of integers. For example, pi is an irrational number.

positive, negative

Predicates to check if number is positive or negative

zero, nonzero

Predicates to heck if a number is zero or not

>>> from sympy import * 
>>> x=Symbol('x') 
>>> x=10 
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)
>>> x,y=symbols("x y") 
>>> x,y=5,10 
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(False, True)
>>> x,y= 2*I, 4+5*I 
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> x,y=5,10 
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)
>>> x,y=5,-5 
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)

Sympy has powerful ability to simplify mathematical expressions. There are many functions in SymPy to perform various kinds of simplification. A general function called simplify() is there that attempts to arrive at the simplest form of an expression.

simplify

This function is defined in sympy.simplify module. simplify() tries to apply intelligent heuristics to make the input expression “simpler”. Following code shows simplifies expression $sin^2(x)+cos^2(x)$.

>>> from sympy import * 
>>> x=Symbol('x')
>>> expr=sin(x)**2 + cos(x)**2 
>>> simplify(expr)

The above code snippet gives the following output −

expand

The expand() is one of the most common simplification functions in SymPy, used in expanding polynomial expressions. For example −

>>> a,b=symbols('a b') 
>>> expand((a+b)**2)

The above code snippet gives an output equivalent to the below expression −

$a^2 + 2ab + b^2$

>>> expand((a+b)*(a-b))

The above code snippet gives an output equivalent to the below expression −

$a^2 - b^2$

The expand() function makes expressions bigger, not smaller. Usually this is the case, but often an expression will become smaller upon calling expand() on it.

>>> expand((x + 1)*(x - 2) - (x - 1)*x)

The above code snippet gives the following output −

-2

factor

This function takes a polynomial and factors it into irreducible factors over the rational numbers.

>>> x,y,z=symbols('x y z') 
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor(expr)

The above code snippet gives an output equivalent to the below expression −

$z(x + 2y)^2$

>>> factor(x**2+2*x+1)

The above code snippet gives an output equivalent to the below expression −

$(x + 1)^2$

The factor() function is the opposite of expand(). Each of the factors returned by factor() is guaranteed to be irreducible. The factor_list() function returns a more structured output.

>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor_list(expr)

The above code snippet gives an output equivalent to the below expression −

(1, [(z, 1), (x + 2*y, 2)])

collect

This function collects additve terms of an expression with respect to a list of expression up to powers with rational exponents.

>>> expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3 
>>> expr

The above code snippet gives an output equivalent to the below expression −

$x^3 + x^2z + 2x^2 + xy + x - 3$

The collect() function on this expression results as follows −

>>> collect(expr,x)

The above code snippet gives an output equivalent to the below expression −

$x^3 + x^2(2 - z) + x(y + 1) - 3$

>>> expr=y**2*x + 4*x*y*z + 4*y**2*z+y**3+2*x*y 
>>> collect(expr,y)

The above code snippet gives an output equivalent to the below expression −

$Y^3+Y^2(x+4z)+y(4xz+2x)$

cancel

The cancel() function will take any rational function and put it into the standard canonical form, p/q, where p and q are expanded polynomials with no common factors. The leading coefficients of p and q do not have denominators i.e., they are integers.

>>> expr1=x**2+2*x+1 
>>> expr2=x+1 
>>> cancel(expr1/expr2)

The above code snippet gives an output equivalent to the below expression −

$x+1$

>>> expr = 1/x + (3*x/2 - 2)/(x - 4) 
>>> expr

The above code snippet gives an output equivalent to the below expression −

$\frac{\frac{3x}{2} - 2}{x - 4} + \frac{1}{x}$

>>> cancel(expr)

The above code snippet gives an output equivalent to the below expression −

$\frac{3x^2 - 2x - 8}{2x^2 - 8}$

>>> expr=1/sin(x)**2 
>>> expr1=sin(x) 
>>> cancel(expr1*expr)

The above code snippet gives an output equivalent to the below expression −

$\frac{1}{\sin(x)}$

trigsimp

This function is used to simplify trigonometric identities. It may be noted that naming conventions for inverse trigonometric functions is to append an a to the front of the function’s name. For example, the inverse cosine, or arc cosine, is called acos().

>>> from sympy import trigsimp, sin, cos 
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2 
>>> trigsimp(expr)

The trigsimp function uses heuristics to apply the best suitable trigonometric identity.

powersimp

This function reduces given expression by combining powers with similar bases and exponents.

>>> expr=x**y*x**z*y**z 
>>> expr

The above code snippet gives an output equivalent to the below expression −

$x^y x^z y^z$

>>> powsimp(expr)

The above code snippet gives an output equivalent to the below expression −

$x^{y+z} y^z$

You can make powsimp() only combine bases or only combine exponents by changing combine=’base’ or combine=’exp’. By default, combine=’all’, which does both.If force is True then bases will be combined without checking for assumptions.

>>> powsimp(expr, combine='base', force=True)

The above code snippet gives an output equivalent to the below expression −

$x^y(xy)^z$

combsimp

Combinatorial expressions involving factorial an binomials can be simplified by using combsimp() function. SymPy provides a factorial() function

>>> expr=factorial(x)/factorial(x - 3) 
>>> expr

The above code snippet gives an output equivalent to the below expression −

$\frac{x!}{(x - 3)!}$

To simplify above combinatorial expression we use combsimp() function as follows −

>>> combsimp(expr)

The above code snippet gives an output equivalent to the below expression −

$x(x-2)(x-1)$

The binomial(x, y) is the number of ways to choose y items from a set of x distinct items. It is also often written as xCy.

>>> binomial(x,y)

The above code snippet gives an output equivalent to the below expression −

$(\frac{x}{y})$

>>> combsimp(binomial(x+1, y+1)/binomial(x, y))

The above code snippet gives an output equivalent to the below expression −

$\frac{x + 1}{y + 1}$

logcombine

This function takes logarithms and combines them using the following rules −

log(x) + log(y) == log(x*y) if both are positive
a*log(x) == log(x**a) if x is positive and a is real

>>> logcombine(a*log(x) + log(y) - log(z))

The above code snippet gives an output equivalent to the below expression −

$a\log(x) + \log(y) - \log(z)$

If force parameter of this function is set to True then the assumptions above will be assumed to hold if there is no assumption already in place on a quantity.

>>> logcombine(a*log(x) + log(y) - log(z), force=True)

The above code snippet gives an output equivalent to the below expression −

$\log\frac{x^a y}{z}$

The derivative of a function is its instantaneous rate of change with respect to one of its variables. This is equivalent to finding the slope of the tangent line to the function at a point.we can find the differentiation of mathematical expressions in the form of variables by using diff() function in SymPy package.

diff(expr, variable)
>>> from sympy import diff, sin, exp 
>>> from sympy.abc import x,y 
>>> expr=x*sin(x*x)+1 >>> expr

The above code snippet gives an output equivalent to the below expression −

$x\sin(x^2) + 1$

>>> diff(expr,x)

The above code snippet gives an output equivalent to the below expression −

$2x^2\cos(x^2) + \sin(x^2)$

>>> diff(exp(x**2),x)

The above code snippet gives an output equivalent to the below expression −

2xe^x²

To take multiple derivatives, pass the variable as many times as you wish to differentiate, or pass a number after the variable.

>>> diff(x**4,x,3)

The above code snippet gives an output equivalent to the below expression −

$24x$

>>> for i in range(1,4): print (diff(x**4,x,i))

The above code snippet gives the below expression −

4*x**3

12*x**2

24*x

It is also possible to call diff() method of an expression. It works similarly as diff() function.

>>> expr=x*sin(x*x)+1 
>>> expr.diff(x)

The above code snippet gives an output equivalent to the below expression −

$2x^2\cos(x^2) + \sin(x^2)$

An unevaluated derivative is created by using the Derivative class. It has the same syntax as diff() function. To evaluate an unevaluated derivative, use the doit method.

>>> from sympy import Derivative 
>>> d=Derivative(expr) 
>>> d

The above code snippet gives an output equivalent to the below expression −

$\frac{d}{dx}(x\sin(x^2)+1)$

>>> d.doit()

The above code snippet gives an output equivalent to the below expression −

$2x^2\cos(x^2) + \sin(x^2)$

The SymPy package contains integrals module. It implements methods to calculate definite and indefinite integrals of expressions. The integrate() method is used to compute both definite and indefinite integrals. To compute an indefinite or primitive integral, just pass the variable after the expression.

For example −

integrate(f, x)

To compute a definite integral, pass the argument as follows −

(integration_variable, lower_limit, upper_limit)

>>> from sympy import * 
>>> x,y = symbols('x y') 
>>> expr=x**2 + x + 1 
>>> integrate(expr, x)

The above code snippet gives an output equivalent to the below expression −

$\frac{x^3}{3} + \frac{x^2}{2} + x$

>>> expr=sin(x)*tan(x) 
>>> expr 
>>> integrate(expr,x)

The above code snippet gives an output equivalent to the below expression −

$-\frac{\log(\sin(x) - 1)}{2} + \frac{\log(\sin(x) + 1)}{2} - \sin(x)$

The example of definite integral is given below −

>>> expr=exp(-x**2) 
>>> integrate(expr,(x,0,oo) )

The above code snippet gives an output equivalent to the below expression −

$\frac{\sqrt\pi}{2}$

You can pass multiple limit tuples to perform a multiple integral. An example is given below −

>>> expr=exp(-x**2 - y**2)
>>> integrate(expr,(x,0,oo),(y,0,oo))

The above code snippet gives an output equivalent to the below expression −

$\frac{\pi}{4}$

You can create unevaluated integral using Integral object, which can be evaluated by calling doit() method.

>>> expr = Integral(log(x)**2, x) 
>>> expr

The above code snippet gives an output equivalent to the below expression −

$\int \mathrm\log(x)^2 \mathrm{d}x$

>>> expr.doit()

The above code snippet gives an output equivalent to the below expression −

$x\log(x)^2 - 2xlog(x) + 2x$

Integral Transforms

SymPy supports various types of integral transforms as follows −

laplace_transform
fourier_transform
sine_transform
cosine_transform
hankel_transform

These functions are defined in sympy.integrals.transforms module. Following examples compute Fourier transform and Laplace transform respectively.

Example 1

>>> from sympy import fourier_transform, exp 
>>> from sympy.abc import x, k 
>>> expr=exp(-x**2) 
>>> fourier_transform(expr, x, k)

On executing the above command in python shell, following output will be generated −

sqrt(pi)*exp(-pi**2*k**2)

Which is equivalent to −

$\sqrt\pi * e^{\pi^2k^2}$

Example 2

>>> from sympy.integrals import laplace_transform 
>>> from sympy.abc import t, s, a 
>>> laplace_transform(t**a, t, s)

On executing the above command in python shell, following output will be generated −

(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)

In Mathematics, a matrix is a two dimensional array of numbers, symbols or expressions. Theory of matrix manipulation deals with performing arithmetic operations on matrix objects, subject to certain rules.

Linear transformation is one of the important applications of matrices. Many scientific fields, specially related to Physics use matrix related applications.

SymPy package has matrices module that deals with matrix handling. It includes Matrix class whose object represents a matrix.

Note: If you want to execute all the snippets in this chapter individually, you need to import the matrix module as shown below −

>>> from sympy.matrices import Matrix

Example

>>> from sympy.matrices import Matrix 
>>> m=Matrix([[1,2,3],[2,3,1]]) 
>>> m
$\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 3 & 1\end{matrix}\right]$

On executing the above command in python shell, following output will be generated −

[1 2 3 2 3 1]

Matrix is created from appropriately sized List objects. You can also obtain a matrix by distributing list items in specified number of rows and columns.

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

On executing the above command in python shell, following output will be generated −

[10 40 30 2 6 9]

Matrix is a mutable object. The matrices module also provides ImmutableMatrix class for obtaining immutable matrix.

Basic manipulation

The shape property of Matrix object returns its size.

>>> M.shape

The output for the above code is as follows −

(2,3)

The row() and col() method respectively returns row or column of specified number.

>>> M.row(0)
$\displaystyle \left[\begin{matrix}10 & 40 & 30\end{matrix}\right]$

The output for the above code is as follows −

[10 40 30]

>>> M.col(1)
$\displaystyle \left[\begin{matrix}40\\6\end{matrix}\right]$

The output for the above code is as follows −

[40 6]

Use Python's slice operator to fetch one or more items belonging to row or column.

>>> M.row(1)[1:3]
[6, 9]

Matrix class has row_del() and col_del() methods that deletes specified row/column from given matrix −

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M.col_del(1) 
>>> M

On executing the above command in python shell, following output will be generated −

Matrix([[10, 30],[ 2, 9]])

You can apply style to the output using the following command −

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

You get the following output after executing the above code snippet −

[10 30 2 9]

>>> M.row_del(0) 
>>> M

$\displaystyle \left[\begin{matrix}2 & 9\end{matrix}\right]$

You get the following output after executing the above code snippet −

[2 9]

Similarly, row_insert() and col_insert() methods add rows or columns at specified row or column index

>>> M1=Matrix([[10,30]]) 
>>> M=M.row_insert(0,M1)
>>> M

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

You get the following output after executing the above code snippet −

[10 40 30 2 9]

>>> M2=Matrix([40,6]) 
>>> M=M.col_insert(1,M2) 
>>> M

$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

You get the following output after executing the above code snippet −

[10 40 30 6 9]

Arithmetic Operations

Usual operators +, - and * are defined for performing addition, subtraction and multiplication.

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5,6],[6,5,4]]) 
>>> M1+M2

$\displaystyle \left[\begin{matrix}5 & 7 & 9\\9 & 7 & 5\end{matrix}\right]$

You get the following output after executing the above code snippet −

[5 7 9 9 7 5]

>>> M1-M2
$\displaystyle \left[\begin{matrix}-3 & -3 & -3\\-3 & -3 & -3\end{matrix}\right]$

You get the following output after executing the above code snippet −

[- 3 -3 -3 -3 -3 -3]

Matrix multiplication is possible only if - The number of columns of the 1st matrix must equal the number of rows of the 2nd matrix. - And the result will have the same number of rows as the 1st matrix, and the same number of columns as the 2nd matrix.

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5],[6,6],[5,4]]) 
>>> M1*M2
$\displaystyle \left[\begin{matrix}31 & 29\\29 & 31\end{matrix}\right]$

The output for the above code is as follows −

[31 29 29 31]

>>> M1.T
$\displaystyle \left[\begin{matrix}1 & 3\\2 & 2\\3 & 1\end{matrix}\right]$

The following output is obtained after executing the code −

[1 3 2 2 3 1]

To calculate a determinant of matrix, use det() method. A determinant is a scalar value that can be computed from the elements of a square matrix.0

>>> M=Matrix(3,3,[10,20,30,5,8,12,9,6,15])
>>> M
$\displaystyle \left[\begin{matrix}10 & 20 & 30\\5 & 8 & 12\\9 & 6 & 15\end{matrix}\right]$

L'output per il codice precedente è il seguente:

[10 20 30 5 8 12 9 6 15]

>>> M.det()

L'output per il codice precedente è il seguente:

-120

Costruttori di matrici

SymPy fornisce molti tipi speciali di classi di matrici. Ad esempio, Matrice di identità, matrice di tutti gli zeri e uno, ecc. Queste classi sono denominate rispettivamente come occhio, zero e uno. La matrice identità è una matrice quadrata con gli elementi che cadono sulla diagonale sono impostati su 1, il resto degli elementi è 0.

Example

from sympy.matrices import eye eye(3)

Output

Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$

L'output per il codice precedente è il seguente:

[1 0 0 0 1 0 0 0 1]

Nella matrice diag, gli elementi sulla diagonale vengono inizializzati secondo gli argomenti forniti.

>>> from sympy.matrices import diag 
>>> diag(1,2,3)

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 2 & 0\\0 & 0 & 3\end{matrix}\right]$

L'output per il codice precedente è il seguente:

[1 0 0 0 2 0 0 0 3]

Tutti gli elementi nella matrice degli zeri vengono inizializzati a 0.

>>> from sympy.matrices import zeros 
>>> zeros(2,3)

$\displaystyle \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]$

L'output per il codice precedente è il seguente:

[0 0 0 0 0 0]

Allo stesso modo, uno è una matrice con tutti gli elementi impostati su 1.

>>> from sympy.matrices import ones
>>> ones(2,3)

$\displaystyle \left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]$

L'output per il codice precedente è il seguente:

[1 1 1 1 1 1]

Il pacchetto Sympy ha la classe Function, che è definita nel modulo sympy.core.function. È una classe base per tutte le funzioni matematiche applicate, come anche un costruttore per classi di funzioni non definite.

Le seguenti categorie di funzioni vengono ereditate dalla classe Function:

Funzioni per numero complesso
Funzioni trigonometriche
Funzioni per numero intero
Funzioni combinatorie
Altre funzioni varie

Funzioni per numero complesso

Questo insieme di funzioni è definito in sympy.functions.elementary.complexes modulo.

Questa funzione restituisce una parte reale di un'espressione -

>>> from sympy import * 
>>> re(5+3*I)

L'output per lo snippet di codice sopra è fornito di seguito:

>>> re(I)

L'output per lo snippet di codice sopra è:

Questa funzione restituisce una parte immaginaria di un'espressione -

>>> im(5+3*I)

L'output per lo snippet di codice sopra è fornito di seguito:

>>> im(I)

L'output per lo snippet di codice sopra è fornito di seguito:

sign

Questa funzione restituisce il segno complesso di un'espressione.

Per una vera espressione, il segno sarà:

1 se l'espressione è positiva
0 se l'espressione è uguale a zero
-1 se l'espressione è negativa

Se l'espressione è immaginaria il segno restituito è -

I se im (espressione) è positiva
-I se im (espressione) è negativo

>>> sign(1.55), sign(-1), sign(S.Zero)

L'output per lo snippet di codice sopra è fornito di seguito:

(1, -1, 0)

>>> sign (-3*I), sign(I*2)

L'output per lo snippet di codice sopra è fornito di seguito:

(-I, I)

Abs

Questa funzione restituisce il valore assoluto di un numero complesso. È definita come la distanza tra l'origine (0,0) e il punto (a, b) nel piano complesso. Questa funzione è un'estensione della funzione incorporata abs () per accettare valori simbolici.

>>> Abs(2+3*I)

L'output per lo snippet di codice sopra è fornito di seguito:

$\sqrt13$

conjugate

Questa funzione restituisce il coniugato di un numero complesso. Per trovare il complesso coniugato cambiamo il segno della parte immaginaria.

>>> conjugate(4+7*I)

Si ottiene il seguente output dopo aver eseguito lo snippet di codice sopra:

4 - 7i

Funzioni trigonometriche

SymPy ha definizioni per tutti i rapporti trigonometrici: sin cos, tan ecc. Così come le sue controparti inverse come asin, acos, atan ecc. Queste funzioni calcolano il rispettivo valore per un dato angolo espresso in radianti.

>>> sin(pi/2), cos(pi/4), tan(pi/6)

L'output per lo snippet di codice sopra è fornito di seguito:

(1, sqrt(2)/2, sqrt(3)/3)

>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)

L'output per lo snippet di codice sopra è fornito di seguito:

(pi/2, pi/4, pi/6)

Funzioni su numero intero

Questo è un insieme di funzioni per eseguire varie operazioni su numeri interi.

ceiling

Questa è una funzione univariata che restituisce il valore intero più piccolo non inferiore al suo argomento. In caso di numeri complessi, limite massimo delle parti reale e immaginaria separatamente.

>>> ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)

L'output per lo snippet di codice sopra è fornito di seguito:

(4, 7, 3 + 4*I)

floor

Questa funzione restituisce il valore intero più grande non maggiore del suo argomento. In caso di numeri complessi, anche questa funzione prende la parola separatamente dalla parte reale e da quella immaginaria.

>>> floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)

L'output per lo snippet di codice sopra è fornito di seguito:

(3, 16, 6 - 6*I)

frac

Questa funzione rappresenta la parte frazionaria di x.

>>> frac(3.99), frac(Rational(10,3)), frac(10)

L'output per lo snippet di codice sopra è fornito di seguito:

(0.990000000000000, 1/3, 0)

Funzioni combinatorie

La combinatoria è un campo della matematica che si occupa di problemi di selezione, disposizione e funzionamento all'interno di un sistema finito o discreto.

factorial

Il fattoriale è molto importante in calcolo combinatorio dove fornisce il numero di modi in cui n oggetti possono essere permutati. È simbolicamente rappresentato come ð ?? '¥! Questa funzione è l'implementazione della funzione fattoriale su interi non negativi, fattoriale di un intero negativo è l'infinito complesso.

>>> x=Symbol('x') 
>>> factorial(x)

L'output per lo snippet di codice sopra è fornito di seguito:

>>> factorial(5)

L'output per lo snippet di codice sopra è fornito di seguito:

120

>>> factorial(-1)

L'output per lo snippet di codice sopra è fornito di seguito:

$\infty\backsim$

binomiale

Questa funzione indica il numero di modi in cui possiamo scegliere k elementi da un insieme di n elementi.

>>> x,y=symbols('x y') 
>>> binomial(x,y)

L'output per lo snippet di codice sopra è fornito di seguito:

$(\frac{x}{y})$

>>> binomial(4,2)

L'output per lo snippet di codice sopra è fornito di seguito:

Righe del triangolo di Pascal possono essere generate con la funzione binomiale.

>>> for i in range(5): print ([binomial(i,j) for j in range(i+1)])

Si ottiene il seguente output dopo aver eseguito lo snippet di codice sopra:

[1]

[1, 1]

[1, 2, 1]

[1, 3, 3, 1]

[1, 4, 6, 4, 1]

fibonacci

I numeri di Fibonacci sono la sequenza intera definita dai termini iniziali F0 = 0, F1 = 1 e dalla relazione di ricorrenza a due termini Fn = Fnâˆ'1 + Fnâˆ'2.

>>> [fibonacci(x) for x in range(10)]

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

tribonacci

I numeri di Tribonacci sono la sequenza intera definita dai termini iniziali F0 = 0, F1 = 1, F2 = 1 e dalla relazione di ricorrenza a tre termini Fn = Fn-1 + Fn-2 + Fn-3.

>>> tribonacci(5, Symbol('x'))

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$x^8 + 3x^5 + 3x^2$

>>> [tribonacci(x) for x in range(10)]

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]

Funzioni varie

Di seguito è riportato un elenco di alcune funzioni utilizzate di frequente:

Min- Restituisce il valore minimo della lista. Si chiama Min per evitare conflitti con la funzione incorporata min.

Max- Restituisce il valore massimo dell'elenco. Si chiama Max per evitare conflitti con la funzione incorporata max.

root - Restituisce l'ennesima radice di x.

sqrt - Restituisce la radice quadrata principale di x.

cbrt - Questa funzione calcola la radice cubica principale di x, (scorciatoia per x ++ Rational (1,3)).

Di seguito sono riportati gli esempi delle funzioni miscellanee di cui sopra e le rispettive uscite:

>>> Min(pi,E)

>>> Max(5, Rational(11,2))

$\frac{11}{2}$

>>> root(7,Rational(1,2))

>>> sqrt(2)

$\sqrt2$

>>> cbrt(1000)

In matematica, il sistema numerico Quaternion è un'estensione di numeri complessi. Ogni oggetto Quaternion contiene quattro variabili scalari e quattro dimensioni, una dimensione reale e tre dimensioni immaginarie.

Il quaternione è rappresentato dalla seguente espressione:

q = a + bi + cj + dk

dove a, b, c ed sono numeri reali e i, j, k sono unità di quaternioni tali che, i2 == j2 == k2 == ijk

Il sympy.algebras.quaternion il modulo ha la classe Quaternion.

>>> from sympy.algebras.quaternion import Quaternion 
>>> q=Quaternion(2,3,1,4) 
>>> q

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$2 + 3i + 1j + 4k$

I quaternioni sono usati nella matematica pura, così come nella matematica applicata, nella computer grafica, nella visione artificiale, ecc.

>>> from sympy import * 
>>> x=Symbol('x') 
>>> q1=Quaternion(x**2, x**3, x) >>> q1

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$x^2 + x^3i + xj + 0k$

L'oggetto quaternione può anche avere coefficienti immaginari

>>> q2=Quaternion(2,(3+2*I), x**2, 3.5*I) 
>>> q2

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$2 + (3 + 2i)i + x2j + 3.5ik$

Inserisci()

Questo metodo disponibile nella classe Quaternion esegue l'aggiunta di due oggetti Quaternion.

>>> q1=Quaternion(1,2,3,4) 
>>> q2=Quaternion(4,3,2,1) 
>>> q1.add(q2)

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$5 + 5i + 5j + 5k$

È possibile aggiungere un numero o un simbolo in un oggetto Quaternion.

>>> q1+2

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

$3 + 2i + 3j + 4k$

>>> q1+x

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

$(x + 1) + 2i + 3j + 4k$

mul ()

Questo metodo esegue la moltiplicazione di due oggetti quaternioni.

>>> q1=Quaternion(1,2,1,2) 
>>> q2=Quaternion(2,4,3,1) 
>>> q1.mul(q2)

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$(-11) + 3i + 11j + 7k$

inverso()

Questo metodo restituisce l'inverso di un oggetto quaternione.

>>> q1.inverse()

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$\frac{1}{10} + (-\frac{1}{5})i + (-\frac{1}{10})j + (-\frac{1}{5})k$

pow ()

Questo metodo restituisce la potenza di un oggetto quaternione.

>>> q1.pow(2)

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

$(-8) + 4i + 2j + 4k$

exp ()

Questo metodo calcola esponenziale di un oggetto Quaternion cioè eq

>>> q=Quaternion(1,2,4,3) 
>>> q.exp()

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

$e\cos(\sqrt29) + \frac{2\sqrt29e\sin(\sqrt29)}{29}i + \frac{4\sqrt29e\sin(\sqrt29)}{29}j + \frac{3\sqrt29e\sin}{29}k$

Poiché i simboli = e == sono definiti come operatori di assegnazione e di uguaglianza in Python, non possono essere usati per formulare equazioni simboliche. SymPy fornisce la funzione Eq () per impostare un'equazione.

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> Eq(x,y)

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

x = y

Poiché x = y è possibile se e solo se xy = 0, l'equazione sopra può essere scritta come -

>>> Eq(x-y,0)

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

x − y = 0

Il modulo risolutore in SymPy fornisce la funzione soveset () il cui prototipo è il seguente:

solveset(equation, variable, domain)

Il dominio è per impostazione predefinita S.Complexes. Usando la funzione solveset (), possiamo risolvere un'equazione algebrica come segue:

>>> solveset(Eq(x**2-9,0), x)

Si ottiene il seguente output:

{−3, 3}

>>> solveset(Eq(x**2-3*x, -2),x)

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

{1,2}

L'output di solveset è un FiniteSet delle soluzioni. Se non ci sono soluzioni, viene restituito un EmptySet

>>> solveset(exp(x),x)

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

$\varnothing$

Equazione lineare

Dobbiamo usare la funzione linsolve () per risolvere equazioni lineari.

Ad esempio, le equazioni sono le seguenti:

xy = 4

x + y = 1

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

La funzione linsolve () può anche risolvere equazioni lineari espresse in forma di matrice.

>>> a,b=symbols('a b') 
>>> a=Matrix([[1,-1],[1,1]]) 
>>> b=Matrix([4,1]) 
>>> linsolve([a,b], (x,y))

Otteniamo il seguente output se eseguiamo lo snippet di codice sopra -

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

Equazione non lineare

A questo scopo, usiamo la funzione nonlinsolve (). Equazioni per questo esempio:

a ² + a = 0 ab = 0

>>> a,b=symbols('a b') 
>>> nonlinsolve([a**2 + a, a - b], [a, b])

Otteniamo il seguente output se eseguiamo lo snippet di codice sopra -

$\lbrace(-1, -1),(0,0)\rbrace$

equazione differenziale

Per prima cosa, crea una funzione indefinita passando cls = Function alla funzione simboli. Per risolvere le equazioni differenziali, usa dsolve.

>>> x=Symbol('x') 
>>> f=symbols('f', cls=Function) 
>>> f(x)

Il seguente output si ottiene dopo aver eseguito lo snippet di codice sopra -

f(x)

Qui f (x) è una funzione non valutata. Il suo derivato è il seguente:

>>> f(x).diff(x)

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$\frac{d}{dx}f(x)$

Per prima cosa creiamo l'oggetto Eq corrispondente alla seguente equazione differenziale

>>> eqn=Eq(f(x).diff(x)-f(x), sin(x)) 
>>> eqn

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$-f(x) + \frac{d}{dx}f(x)= \sin(x)$

>>> dsolve(eqn, f(x))

Lo snippet di codice sopra fornisce un output equivalente all'espressione seguente -

$f(x)=(c^1-\frac{e^-xsin(x)}{2}-\frac{e^-xcos(x)}{2})e^x$

SymPy utilizza la libreria Matplotlib come backend per eseguire il rendering di grafici 2-D e 3-D di funzioni matematiche. Assicurati che Matplotlib sia disponibile nell'installazione corrente di Python. In caso contrario, installa lo stesso utilizzando il seguente comando:

pip install matplotlib

Il supporto per il plottaggio è definito nel modulo sympy.plotting. Le seguenti funzioni sono presenti nel modulo di plottaggio:

plot - Grafici a linee 2D
plot3d - Grafici a linee 3D
plot_parametric - Grafici parametrici 2D
plot3d_parametric - Grafici parametrici 3D

La funzione plot () restituisce un'istanza della classe Plot. Una figura della trama può avere una o più espressioni SymPy. Sebbene sia in grado di utilizzare Matplotlib come backend, possono essere utilizzati anche altri backend come texplot, pyglet o l'API dei grafici di Google.

plot(expr, range, kwargs)

dove expr è una qualsiasi espressione symPy valida. Se non menzionato, l'intervallo usa l'impostazione predefinita come (-10, 10).

L'esempio seguente traccia i valori di x2 per ogni valore nell'intervallo (-10,10) -

>>> from sympy.plotting import plot 
>>> from sympy import * 
>>> x=Symbol('x') 
>>> plot(x**2, line_color='red')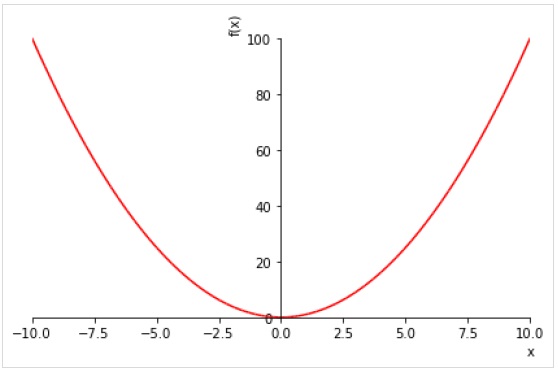

Per disegnare più grafici per lo stesso intervallo, fornire più espressioni prima della tupla di intervallo.

>>> plot( sin(x),cos(x), (x, -pi, pi))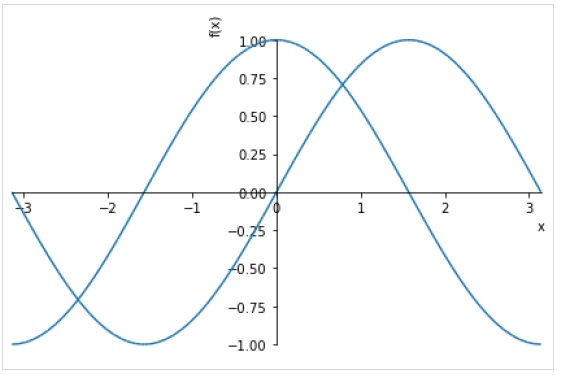

È inoltre possibile specificare un intervallo separato per ciascuna espressione.

plot((expr1, range1), (expr2, range2))

La figura seguente traccia sin (x) e cos (x) su intervalli diversi.

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)))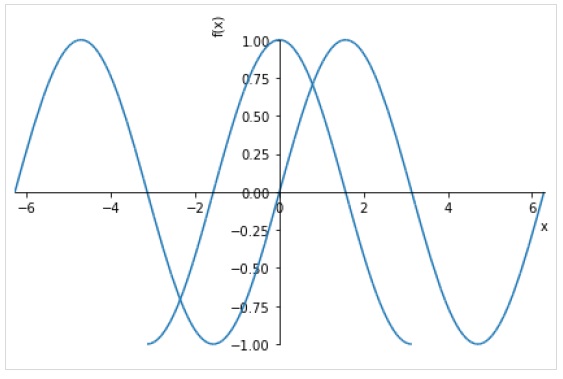

I seguenti argomenti di parole chiave opzionali possono essere specificati nella funzione plot ().

line_color - specifica il colore della linea di trama.
title - una stringa da visualizzare come titolo
xlabel - una stringa da visualizzare come etichetta per l'asse X.
ylabel - una stringa da visualizzare come etichetta per l'asse y

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)), line_color='red', title='SymPy plot example')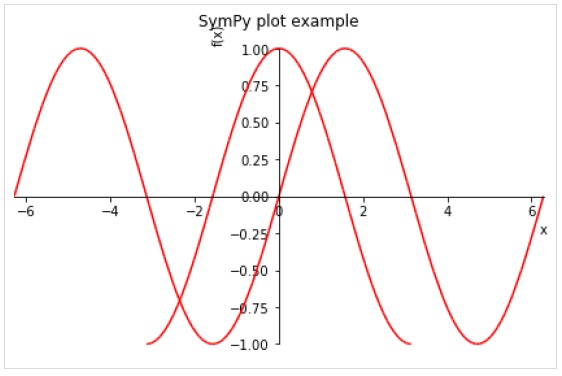

La funzione plot3d () rende un grafico tridimensionale.

plot3d(expr, xrange, yrange, kwargs)

L'esempio seguente disegna un grafico di superficie 3D:

>>> from sympy.plotting import plot3d 
>>> x,y=symbols('x y') 
>>> plot3d(x*y, (x, -10,10), (y, -10,10))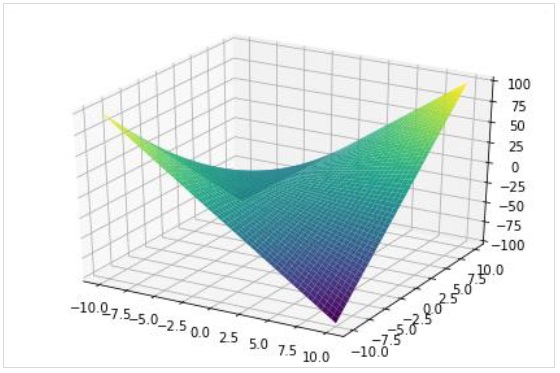

Come nel grafico 2D, un grafico tridimensionale può anche avere più grafici ciascuno con un intervallo diverso.

>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))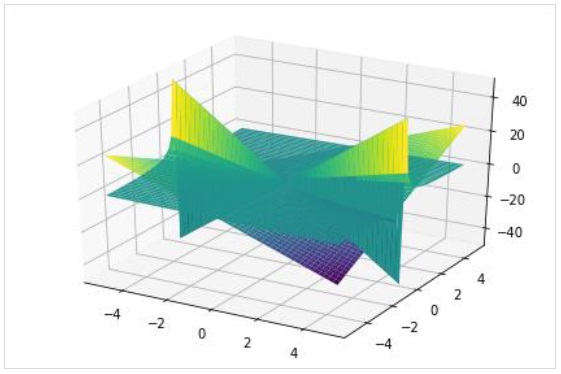

La funzione plot3d_parametric_line () esegue il rendering di un grafico a linee parametriche tridimensionali.

>>> from sympy.plotting import plot3d_parametric_line 
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))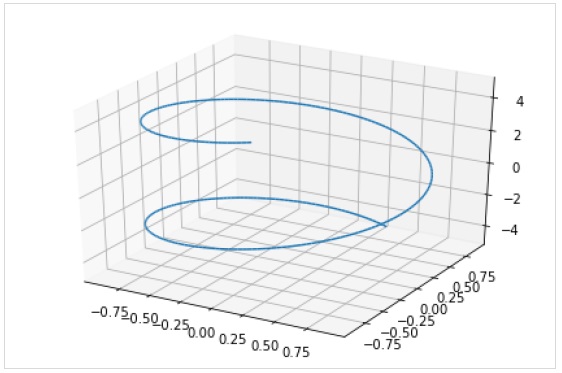

Per disegnare un grafico di superficie parametrico, utilizzare la funzione plot3d_parametric_surface ().

plot3d_parametric_surface(xexpr, yexpr, zexpr, rangex, rangey, kwargs)

>>> from sympy.plotting import plot3d_parametric_surface 
>>> plot3d_parametric_surface(cos(x+y), sin(x-y), x-y, (x, -5, 5), (y, -5, 5))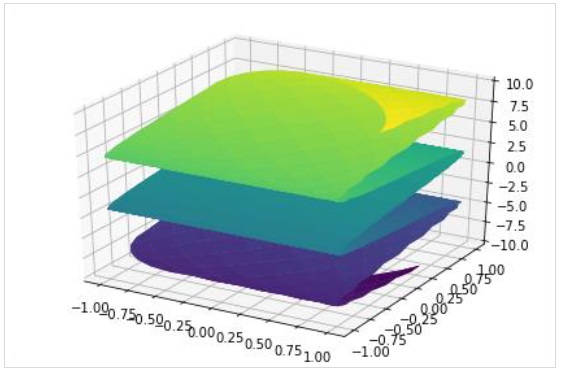

Il modulo di geometria in SymPy consente la creazione di entità bidimensionali come linea, cerchio, ecc. Possiamo quindi ottenere informazioni su di esse come il controllo della colinearità o la ricerca dell'intersezione.

Punto

La classe Point rappresenta un punto nello spazio euclideo. Il seguente esempio controlla la collinearità dei punti:

>>> from sympy.geometry import Point 
>>> from sympy import * 
>>> x=Point(0,0) 
>>> y=Point(2,2) 
>>> z=Point(4,4) 
>>> Point.is_collinear(x,y,z)

Output

True

>>> a=Point(2,3) 
>>> Point.is_collinear(x,y,a)

Output

False

Il metodo distance () della classe Point calcola la distanza tra due punti

>>> x.distance(y)

Output

$2\sqrt2$

La distanza può anche essere rappresentata in termini di simboli.

Linea

L'entità linea è ottenuta da due oggetti Point. Il metodo intersection () restituisce il punto di intersezione se due linee si intersecano.

>>> from sympy.geometry import Point, Line 
>>> p1, p2=Point(0,5), Point(5,0) 
>>> l1=Line(p1,p2)
>>> l2=Line(Point(0,0), Point(5,5)) 
>>> l1.intersection(l2)

Output

[Point2D(5/2, 5/2)]

>>> l1.intersection(Line(Point(0,0), Point(2,2)))

Output

[Point2D(5/2, 5/2)]

>>> x,y=symbols('x y') 
>>> p=Point(x,y) 
>>> p.distance(Point(0,0))

Output

$\sqrt{x^2 + y^2}$

Triangolo

Questa funzione crea un'entità triangolo da tre oggetti punto.

Triangle(a,b,c)

>>> t=Triangle(Point(0,0),Point(0,5), Point(5,0)) 
>>> t.area

Output

$-\frac{25}{2}$

Ellisse

Un'entità di geometria ellittica viene costruita passando un oggetto Point corrispondente al centro e due numeri ciascuno per il raggio orizzontale e verticale.

ellipse(center, hradius, vradius)

>>> from sympy.geometry import Ellipse, Line 
>>> e=Ellipse(Point(0,0),8,3) 
>>> e.area

Output

$24\pi$

Il vradius può essere fornito indirettamente utilizzando il parametro di eccentricità.

>>> e1=Ellipse(Point(2,2), hradius=5, eccentricity=Rational(3,4)) 
>>> e1.vradius

Output

$\frac{5\sqrt7}{4}$

Il apoapsis dell'ellisse è la distanza massima tra il fuoco e il contorno.

>>> e1.apoapsis

Output

$\frac{35}{4}$

La seguente dichiarazione calcola la circonferenza dell'ellisse -

>>> e1.circumference

Output

$20E(\frac{9}{16})$

Il equation il metodo dell'ellisse restituisce l'equazione dell'ellisse.

>>> e1.equation(x,y)

Output

$(\frac{x}{5}-\frac{2}{5})^2 + \frac{16(y-2)2}{175} - 1$

In matematica, un set è una raccolta ben definita di oggetti distinti che possono essere numeri, persone, lettere dell'alfabeto o anche altri set. Set è anche uno dei tipi incorporati in Python. SymPy fornisce il modulo degli insiemi. Contiene definizioni di diversi tipi di insieme e ha funzionalità per eseguire operazioni di insieme come intersezione, unione, ecc.

Set è una classe base per qualsiasi altro tipo di set in SymPy. Si noti che è diverso dal tipo di dati impostato incorporato di Python. La classe Interval rappresenta gli intervalli reali e la sua proprietà boundary restituisce aFiniteSet oggetto.

>>> from sympy import Interval 
>>> s=Interval(1,10).boundary 
>>> type(s)

sympy.sets.sets.FiniteSet

FiniteSet è una raccolta di numeri discreti. Può essere ottenuto da qualsiasi oggetto sequenza come elenco o stringa.

>>> from sympy import FiniteSet 
>>> FiniteSet(range(5))

Output

$\lbrace\lbrace0,1,...,4\rbrace\rbrace$

>>> numbers=[1,3,5,2,8] 
>>> FiniteSet(*numbers)

Output

$\lbrace1,2,3,5,8\rbrace$

>>> s="HelloWorld" 
>>> FiniteSet(*s)

Output

{H,W,d,e,l,o,r}

Nota che, come nel set integrato, anche SymPy's Set è una raccolta di oggetti distinti.

ConditionSet è un insieme di elementi che soddisfano una data condizione

>>> from sympy import ConditionSet, Eq, Symbol 
>>> x=Symbol('x') 
>>> s=ConditionSet(x, Eq(x**2-2*x,0), Interval(1,10)) >>> s

Output

$\lbrace x\mid x\in[1,10]∧x^2 - 2x =0\rbrace$

Unionè un insieme composto. Include tutti gli elementi in due set. Tieni presente che gli elementi che si trovano in entrambi appariranno solo una volta nell'Unione.

>>> from sympy import Union 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Union(a,b)

Intersection d'altra parte contiene solo quegli elementi che sono presenti in entrambi.

>>> from sympy import Intersection 
>>> Intersection(a,b)

ProductSet oggetto rappresenta il prodotto cartesiano di elementi in entrambi gli insiemi.

>>> from sympy import ProductSet 
>>> l1=[1,2] 
>>> l2=[2,3] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> set(ProductSet(a,b))

Complement(a,b) mantiene gli elementi in a escludendo gli elementi comuni con l'insieme b.

>>> from sympy import Complement 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Complement(a,b), Complement(b,a)

SymmetricDifference set contiene solo elementi non comuni in entrambi i set.

>>> from sympy import SymmetricDifference 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> SymmetricDifference(a,b)

Output

{2,3,5,9}

Sono disponibili diverse stampanti in SymPy. Di seguito è riportato un elenco parziale:

str
srepr
Bella stampante ASCII
Bella stampante Unicode
LaTeX
MathML
Dot

Gli oggetti SymPy possono anche essere inviati come output al codice di vari linguaggi, come C, Fortran, Javascript, Theano e Python.

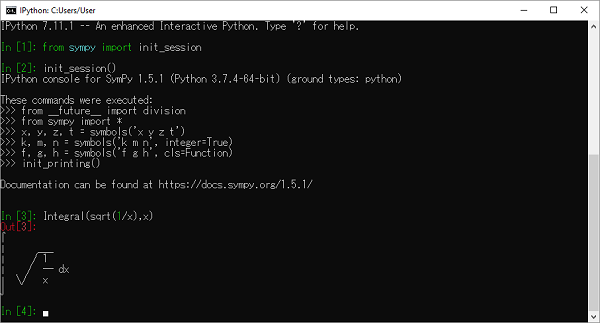
SymPy utilizza i caratteri Unicode per rendere l'output sotto forma di una bella stampa. Se stai usando la console Python per eseguire la sessione SymPy, il miglior ambiente di stampa carino viene attivato chiamando la funzione init_session ().

>>> from sympy import init_session 
>>> init_session()

Console IPython per SymPy 1.5.1 (Python 3.7.4-64 bit) (tipi di base: python).

Questi comandi sono stati eseguiti:

>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()

La documentazione può essere trovata su https://docs.sympy.org/1.5.1/.

>>> Integral(sqrt(1/x),x)

$\int \sqrt\frac{1}{x} dx$

Se LATEX non è installato, ma Matplotlib è installato, utilizzerà il motore di rendering Matplotlib. Se Matplotlib non è installato, utilizza la graziosa stampante Unicode. Tuttavia, il notebook Jupyter utilizza MathJax per eseguire il rendering di LATEX.

In un terminale che non supporta Unicode, viene utilizzata una bella stampante ASCII.

Per utilizzare la stampante ASCII, utilizzare la funzione pprint () con la proprietà use_unicode impostata su False

>>> pprint(Integral(sqrt(1/x),x),use_unicode=False)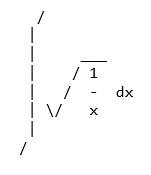

La stampante Unicode pretty è accessibile anche da pprint () e pretty (). Se il terminale supporta Unicode, viene utilizzato automaticamente. Se pprint () non è in grado di rilevare che il terminale supporta Unicode, puoi passare use_unicode = True per forzarlo a usare Unicode.

Per ottenere la forma LATEX di un'espressione, usa la funzione latex ().

>>> print(latex(Integral(sqrt(1/x),x)))

\int \sqrt{\frac{1}{x}}\, dx

Puoi anche usare mathml printer. a tale scopo, importa la funzione print_mathml. Una versione stringa è ottenuta dalla funzione mathml ().

>>> from sympy.printing.mathml import print_mathml 
>>> print_mathml(Integral(sqrt(1/x),x))

<apply>

<int/>

<bvar>

<ci>x</ci>

</bvar>

<apply>

<root/>

<apply>

<power/>

<ci>x</ci>

<cn>-1</cn>

</apply>

>>>mathml(Integral(sqrt(1/x),x))

'<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn>-1</cn></apply></apply></apply>'