TensorFlow - Formazione di grafici

Un'equazione differenziale parziale (PDE) è un'equazione differenziale, che coinvolge derivate parziali con funzione sconosciuta di diverse variabili indipendenti. Con riferimento alle equazioni alle derivate parziali, ci concentreremo sulla creazione di nuovi grafici.

Supponiamo che ci sia uno stagno con dimensioni 500 * 500 quadrati -

N = 500

Ora, calcoleremo l'equazione differenziale parziale e formeremo il rispettivo grafico usandola. Considera i passaggi indicati di seguito per il calcolo del grafico.

Step 1 - Importa librerie per la simulazione.

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

Step 2 - Include funzioni per la trasformazione di un array 2D in un kernel di convoluzione e un'operazione di convoluzione 2D semplificata.

def make_kernel(a):
   a = np.asarray(a)
   a = a.reshape(list(a.shape) + [1,1])
   return tf.constant(a, dtype=1)

def simple_conv(x, k):
   """A simplified 2D convolution operation"""
   x = tf.expand_dims(tf.expand_dims(x, 0), -1)
   y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME')
   return y[0, :, :, 0]

def laplace(x):
   """Compute the 2D laplacian of an array"""
   laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]])
   return simple_conv(x, laplace_k)
   
sess = tf.InteractiveSession()

Step 3 - Includere il numero di iterazioni e calcolare il grafico per visualizzare i record di conseguenza.

N = 500

# Initial Conditions -- some rain drops hit a pond

# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)

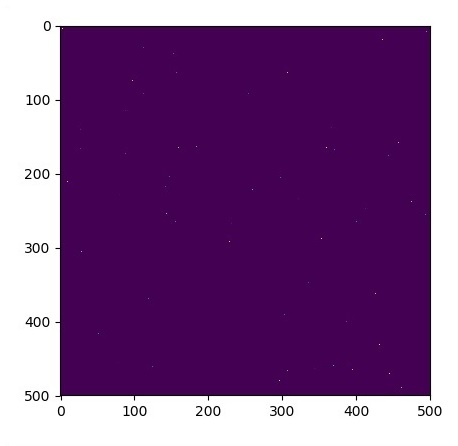
# Some rain drops hit a pond at random points
for n in range(100):
   a,b = np.random.randint(0, N, 2)
   u_init[a,b] = np.random.uniform()

plt.imshow(u_init)
plt.show()

# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())

# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)

# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)

# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))

# Initialize state to initial conditions
tf.initialize_all_variables().run()

# Run 1000 steps of PDE
for i in range(1000):
   # Step simulation
   step.run({eps: 0.03, damping: 0.04})
   
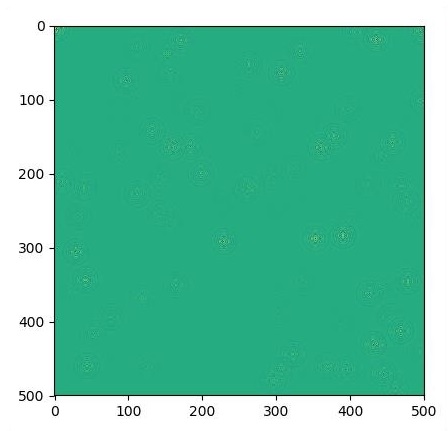
   # Visualize every 50 steps
   if i % 500 == 0:
      plt.imshow(U.eval())
      plt.show()

I grafici vengono tracciati come mostrato di seguito: