Pythonを使用したAI–時系列データの分析

与えられた入力シーケンスの次を予測することは、機械学習におけるもう1つの重要な概念です。この章では、時系列データの分析について詳しく説明します。

前書き

時系列データとは、一連の特定の時間間隔にあるデータを意味します。機械学習でシーケンス予測を構築する場合は、シーケンシャルデータと時間を処理する必要があります。系列データは、順次データの要約です。データの順序付けは、シーケンシャルデータの重要な機能です。

配列分析または時系列分析の基本概念

シーケンス分析または時系列分析は、以前に観察されたものに基づいて、特定の入力シーケンスの次のシーケンスを予測することです。予測は、記号、数字、翌日の天気、スピーチの次の用語など、次に来る可能性のあるものであれば何でもかまいません。シーケンス分析は、株式市場分析、天気予報、製品の推奨などのアプリケーションで非常に便利です。

Example

シーケンス予測を理解するために、次の例を検討してください。ここにA,B,C,D 与えられた値であり、値を予測する必要があります E シーケンス予測モデルを使用します。

便利なパッケージのインストール

Pythonを使用した時系列データ分析では、次のパッケージをインストールする必要があります-

パンダ

Pandasは、Python用の高性能で簡単なデータ構造の使用とデータ分析ツールを提供するオープンソースのBSDライセンスライブラリです。次のコマンドを使用してパンダをインストールできます-

pip install pandas

Anacondaを使用していて、を使用してインストールする場合 conda パッケージマネージャーの場合、次のコマンドを使用できます-

conda install -c anaconda pandas

hmmlearn

これは、Pythonで隠れマルコフモデル（HMM）を学習するための単純なアルゴリズムとモデルで構成されるオープンソースのBSDライセンスライブラリです。次のコマンドを使用してインストールできます-

pip install hmmlearn

Anacondaを使用していて、を使用してインストールする場合 conda パッケージマネージャーの場合、次のコマンドを使用できます-

conda install -c omnia hmmlearn

PyStruct

これは、構造化された学習および予測ライブラリです。PyStructに実装されている学習アルゴリズムには、条件付き確率場（CRF）、最大マージンマルコフ確率場（M3N）、構造サポートベクターマシンなどの名前があります。次のコマンドを使用してインストールできます-

pip install pystruct

CVXOPT

Pythonプログラミング言語に基づく凸最適化に使用されます。また、無料のソフトウェアパッケージです。次のコマンドを使用してインストールできます-

pip install cvxopt

Anacondaを使用していて、を使用してインストールする場合 conda パッケージマネージャーの場合、次のコマンドを使用できます-

conda install -c anaconda cvdoxt

パンダ：時系列データからの統計の処理、スライス、抽出

Pandasは、時系列データを操作する必要がある場合に非常に便利なツールです。パンダの助けを借りて、あなたは以下を実行することができます-

  • を使用して日付の範囲を作成します pd.date_range パッケージ

  • を使用してパンダに日付のインデックスを付ける pd.Series パッケージ

  • を使用してリサンプリングを実行します ts.resample パッケージ

  • 頻度を変更する

例

次の例は、Pandasを使用して時系列データを処理およびスライスする方法を示しています。ここでは、monthly.ao.index.b50.current.asciiからダウンロードでき、使用するためにテキスト形式に変換できる月次北極振動データを使用していることに注意してください。

時系列データの処理

時系列データを処理するには、次の手順を実行する必要があります-

最初のステップでは、次のパッケージをインポートします-

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

次に、以下のコードに示すように、入力ファイルからデータを読み取る関数を定義します。

def read_data(input_file):
   input_data = np.loadtxt(input_file, delimiter = None)

次に、このデータを時系列に変換します。このために、時系列の日付の範囲を作成します。この例では、データの頻度として1か月を保持します。私たちのファイルには、1950年1月から始まるデータが含まれています。

dates = pd.date_range('1950-01', periods = input_data.shape[0], freq = 'M')

このステップでは、以下に示すように、Pandasシリーズを使用して時系列データを作成します。

output = pd.Series(input_data[:, index], index = dates)	
return output
	
if __name__=='__main__':

ここに示すように、入力ファイルのパスを入力します-

input_file = "/Users/admin/AO.txt"

次に、次に示すように、列を時系列形式に変換します。

timeseries = read_data(input_file)

最後に、示されているコマンドを使用して、データをプロットして視覚化します。

plt.figure()
timeseries.plot()
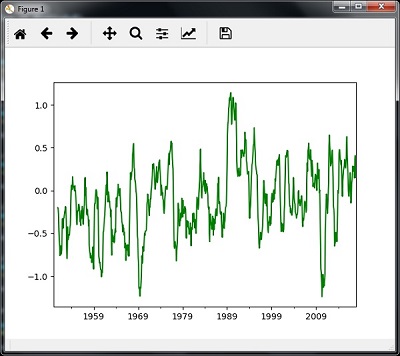
plt.show()

次の画像に示すようにプロットを観察します-

時系列データのスライス

スライスには、時系列データの一部のみを取得することが含まれます。例の一部として、1980年から1990年までのデータのみをスライスしています。このタスクを実行する次のコードを確認してください。

timeseries['1980':'1990'].plot()
   <matplotlib.axes._subplots.AxesSubplot at 0xa0e4b00>

plt.show()

時系列データをスライスするためのコードを実行すると、次の画像に示すような次のグラフを確認できます。

時系列データからの統計の抽出

重要な結論を出す必要がある場合は、特定のデータからいくつかの統計を抽出する必要があります。平均、分散、相関、最大値、および最小値は、そのような統計の一部です。特定の時系列データからそのような統計を抽出する場合は、次のコードを使用できます-

平均

あなたは使用することができます mean() ここに示すように、平均を見つけるための関数-

timeseries.mean()

次に、説明した例で観察される出力は次のとおりです。

-0.11143128165238671

最大

あなたは使用することができます max() ここに示すように、最大​​値を見つけるための関数-

timeseries.max()

次に、説明した例で観察される出力は次のとおりです。

3.4952999999999999

最小

次に示すように、最小値を見つけるためにmin（）関数を使用できます。

timeseries.min()

次に、説明した例で観察される出力は次のとおりです。

-4.2656999999999998

すべてを一度に取得

一度にすべての統計を計算したい場合は、 describe() ここに示すように機能します-

timeseries.describe()

次に、説明した例で観察される出力は次のとおりです。

count   817.000000
mean     -0.111431
std       1.003151
min      -4.265700
25%      -0.649430
50%      -0.042744
75%       0.475720
max       3.495300
dtype: float64

リサンプリング

データを別の時間頻度にリサンプリングできます。リサンプリングを実行するための2つのパラメータは次のとおりです。

  • 期間
  • Method

mean（）によるリサンプリング

次のコードを使用して、デフォルトのメソッドであるmean（）メソッドでデータをリサンプリングできます。

timeseries_mm = timeseries.resample("A").mean()
timeseries_mm.plot(style = 'g--')
plt.show()

次に、mean（）−を使用したリサンプリングの出力として次のグラフを確認できます。

median（）を使用したリサンプリング

次のコードを使用して、を使用してデータをリサンプリングできます。 median()方法−

timeseries_mm = timeseries.resample("A").median()
timeseries_mm.plot()
plt.show()

次に、median（）−を使用したリサンプリングの出力として次のグラフを確認できます。

移動平均

次のコードを使用して、ローリング（移動）平均を計算できます-

timeseries.rolling(window = 12, center = False).mean().plot(style = '-g')
plt.show()

次に、ローリング（移動）平均の出力として次のグラフを観察できます。

隠れマルコフモデル（HMM）によるシーケンシャルデータの分析

HMMは、時系列の株式市場分析、健康診断、音声認識など、継続性と拡張性を備えたデータに広く使用されている統計モデルです。このセクションでは、隠れマルコフモデル（HMM）を使用したシーケンシャルデータの分析について詳しく説明します。

隠れマルコフモデル（HMM）

HMMは、将来の統計の確率が現在のプロセス状態にのみ依存し、それ以前の状態には依存しないという仮定に基づいて、マルコフ連鎖の概念に基づいて構築された確率モデルです。たとえば、コインを投げるとき、5回目の投げの結果が頭になるとは言えません。これは、コインにメモリがなく、次の結果が前の結果に依存しないためです。

数学的には、HMMは次の変数で構成されます-

州（S）

これは、HMMに存在する隠れ状態または潜在状態のセットです。Sで表されます。

出力記号（O）

これは、HMMに存在する可能性のある出力シンボルのセットです。Oで表されます。

状態遷移確率行列（A）

これは、ある状態から他の各状態に遷移する確率です。Aで表されます。

観測放出確率行列（B）

これは、特定の状態でシンボルを放出/観測する確率です。Bで表されます。

事前確率行列（Π）

これは、システムのさまざまな状態から特定の状態で開始する確率です。Πで表されます。

したがって、HMMは次のように定義できます。 = (S,O,A,B,)、

どこ、

  • S = {s1,s2,…,sN} N個の可能な状態のセットです。
  • O = {o1,o2,…,oM} M個の可能な観測記号のセットです。
  • Aは NN 状態遷移確率行列（TPM）、
  • Bは NM 観測または放出確率行列（EPM）、
  • πはN次元の初期状態確率分布ベクトルです。

例：株式市場データの分析

この例では、株式市場のデータを段階的に分析して、HMMがシーケンシャルデータまたは時系列データでどのように機能するかを理解します。この例はPythonで実装していることに注意してください。

以下に示すように、必要なパッケージをインポートします-

import datetime
import warnings

次に、からの株式市場データを使用します。 matpotlib.finance ここに示すように、パッケージ-

import numpy as np
from matplotlib import cm, pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator
try:
   from matplotlib.finance import quotes_historical_yahoo_och1
except ImportError:
   from matplotlib.finance import (
      quotes_historical_yahoo as quotes_historical_yahoo_och1)

from hmmlearn.hmm import GaussianHMM

開始日と終了日から、つまりここに示すように2つの特定の日付の間でデータをロードします-

start_date = datetime.date(1995, 10, 10)
end_date = datetime.date(2015, 4, 25)
quotes = quotes_historical_yahoo_och1('INTC', start_date, end_date)

このステップでは、終値を毎日抽出します。これには、次のコマンドを使用します-

closing_quotes = np.array([quote[2] for quote in quotes])

ここで、毎日取引される株式の量を抽出します。これには、次のコマンドを使用します-

volumes = np.array([quote[5] for quote in quotes])[1:]

ここでは、以下に示すコードを使用して、終値のパーセンテージの差を取ります-

diff_percentages = 100.0 * np.diff(closing_quotes) / closing_quotes[:-]
dates = np.array([quote[0] for quote in quotes], dtype = np.int)[1:]
training_data = np.column_stack([diff_percentages, volumes])

このステップでは、ガウスHMMを作成してトレーニングします。これには、次のコードを使用します-

hmm = GaussianHMM(n_components = 7, covariance_type = 'diag', n_iter = 1000)
with warnings.catch_warnings():
   warnings.simplefilter('ignore')
   hmm.fit(training_data)

次に、示されているコマンドを使用して、HMMモデルを使用してデータを生成します。

num_samples = 300
samples, _ = hmm.sample(num_samples)

最後に、このステップでは、グラフの形式で出力として取引された株式の差の割合と量をプロットして視覚化します。

次のコードを使用して、差異のパーセンテージをプロットおよび視覚化します-

plt.figure()
plt.title('Difference percentages')
plt.plot(np.arange(num_samples), samples[:, 0], c = 'black')

次のコードを使用して、取引された株式の量をプロットして視覚化します-

plt.figure()
plt.title('Volume of shares')
plt.plot(np.arange(num_samples), samples[:, 1], c = 'black')
plt.ylim(ymin = 0)
plt.show()
ja/tutorial
es/tutorial
de/tutorial
fr/tutorial
th/tutorial
pt/tutorial
ru/tutorial
vi/tutorial
it/tutorial
ko/tutorial
tr/tutorial
id/tutorial
pl/tutorial
hi/tutorial
japost
espost
depost
frpost
thpost
ptpost
rupost
vipost
itpost
kopost
trpost
idpost
plpost
hipost

© Copyright 2021 - 2024 | All Rights Reserved