リミッターと電圧マルチプライヤ
クリッパーやクランパーなどの波形整形回路に加えて、ダイオードを使用して、リミッターや電圧逓倍器などの他の回路を構築します。これについては、この章で説明します。ダイオードには、整流器と呼ばれる別の重要なアプリケーションもあります。これについては後で説明します。
リミッター
これらのクリッパーやクランパーを通過するときによく出くわすもう1つの名前は、リミッター回路です。Alimiter 回路は、出力電圧が所定の値を超えないように制限する回路として理解できます。
これは多かれ少なかれ、信号の指定された値を超えることを許可しないクリッパー回路です。実際には、クリッピングは極端な制限の範囲と言えます。したがって、制限はスムーズなクリッピングとして理解できます。
次の画像は、リミッター回路のいくつかの例を示しています-
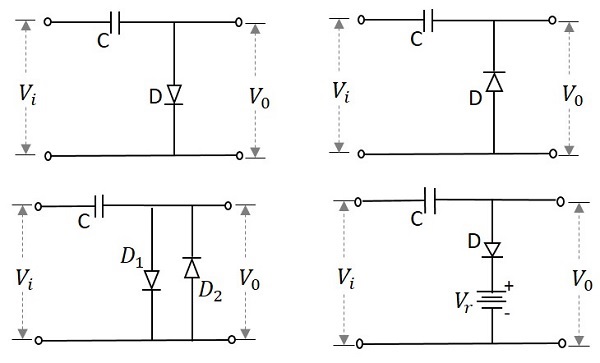
リミッター回路の性能は、その伝達特性曲線から理解できます。このような曲線の例は次のとおりです。
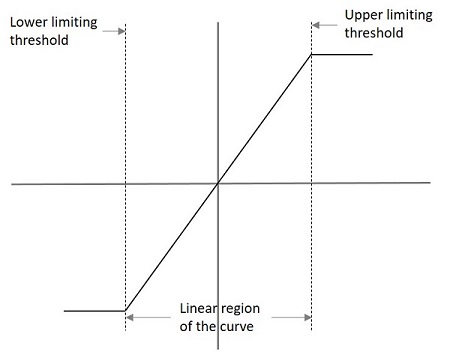
リミッターの特性を示す下限と上限がグラフに示されています。このようなグラフの出力電圧は、次のように理解できます。
$$ V_ {0} = L _ {-}、KV_ {i}、L _ {+} $$
どこ
$$ L _ {-} = V_ {i} \ leq \ frac {L _ {-}} {k} $$
$$ KV_ {i} = \ frac {L _ {-}} {k} <V_ {i} <\ frac {L _ {+}} {k} $$
$$ L _ {+} = V_ {i} \ geq \ frac {L _ {+}} {K} $$
リミッターの種類
のようなリミッターのいくつかのタイプがあります
Unipolar Limiter −この回路は信号を一方向に制限します。
Bipolar Limiter −この回路は2つの方法で信号を制限します。
Soft Limiter −この回路では、入力がわずかに変化しても、出力が変化する場合があります。
Hard Limiter −入力信号の変化に伴って出力が変化しにくい。
Single Limiter −この回路は制限用に1つのダイオードを採用しています。
Double Limiter −この回路は制限用に2つのダイオードを採用しています。
電圧逓倍器
場合によっては、電圧を乗算する必要があるアプリケーションがあります。これは、ダイオードとコンデンサを使用した単純な回路の助けを借りて簡単に行うことができます。電圧が2倍になると、そのような回路は電圧ダブラと呼ばれます。これを拡張して、VoltageTriplerやVoltageQuadruplerなどを作成し、高いDC電圧を得ることができます。
理解を深めるために、電圧を2倍にする回路を考えてみましょう。この回路は、 Voltage Doubler。次の図は、電圧ダブラの回路を示しています。
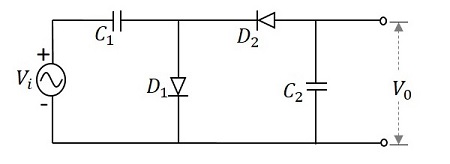
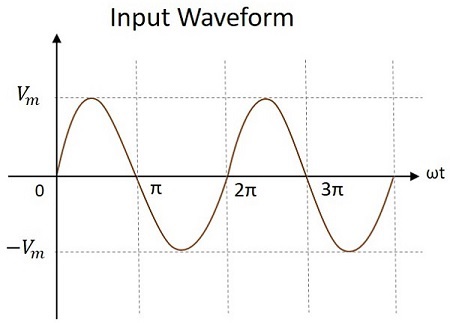
印加される入力電圧は、下図に示すように正弦波の形のAC信号になります。
ワーキング
電圧逓倍回路は、入力信号の各半サイクルを分析することで理解できます。各サイクルにより、ダイオードとコンデンサは異なる方法で動作します。これを理解してみましょう。
During the first positive half cycle−入力信号が印加されると、コンデンサ$ C_ {1} $が充電され、ダイオード$ D_ {1} $が順方向にバイアスされます。ダイオード$ D_ {2} $は逆バイアスされ、コンデンサ$ C_ {2} $は電荷を取得しません。これにより、出力$ V_ {0} $は$ V_ {m} $になります
これは次の図から理解できます。
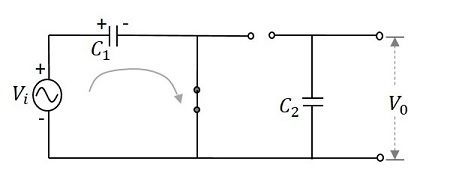
したがって、0から$ \ pi $の間、生成される出力電圧は$ V_ {max} $になります。コンデンサ$ C_ {1} $は、順方向にバイアスされたダイオード$ D_ {1} $を介して充電され、出力を提供しますが、$ C_ {2} $は充電されません。この電圧は出力に現れます。
During the negative half cycle−その後、負の半サイクルが到来すると、ダイオード$ D_ {1} $は逆バイアスされ、ダイオード$ D_ {2} $は順バイアスされます。ダイオード$ D_ {2} $は、このプロセス中に充電されるコンデンサ$ C_ {2} $を介して電荷を取得します。次に、電流はコンデンサ$ C_ {1} $を流れて放電します。次の図から理解できます。
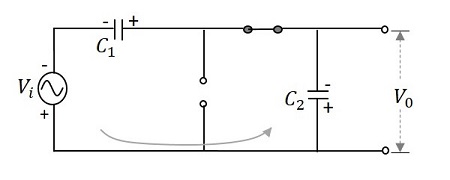
したがって、$ \ pi $から$ 2 \ pi $の間、コンデンサ$ C_ {2} $の両端の電圧は$ V_ {max} $になります。完全に充電されているコンデンサ$ C_ {1} $は放電する傾向がありますが、これで、両方のコンデンサからの電圧が一緒に出力に現れます。これは$ 2V_ {max} $です。したがって、このサイクル中の出力電圧$ V_ {0} $は$ 2V_ {max} $です。
During the next positive half cycle−コンデンサ$ C_ {1} $は電源から充電され、ダイオード$ D_ {1} $は順方向にバイアスされます。コンデンサ$ C_ {2} $は、放電する方法が見つからず、ダイオード$ D_ {2} $が逆バイアスされるため、電荷を保持します。ここで、このサイクルの出力電圧$ V_ {0} $は、出力に一緒に現れる両方のコンデンサからの電圧、つまり$ 2V_ {max} $を取得します。
During the next negative half cycle−次の負の半サイクルにより、コンデンサ$ C_ {1} $は再び完全充電から放電し、ダイオード$ D_ {1} $は逆バイアスになり、$ D_ {2} $は順方向にコンデンサ$ C_ {2} $になります。その電圧を維持するためにさらに充電します。ここで、このサイクルの出力電圧$ V_ {0} $は、出力に一緒に現れる両方のコンデンサからの電圧、つまり$ 2V_ {max} $を取得します。
したがって、出力電圧$ V_ {0} $は、動作中ずっと$ 2V_ {max} $に維持され、回路の電圧が2倍になります。
電圧逓倍器は主に、高いDC電圧が必要な場合に使用されます。たとえば、ブラウン管やコンピューターディスプレイ。
分圧器
ダイオードを使用して電圧を乗算しますが、直列抵抗のセットを小さなネットワークにして電圧を分割することができます。このようなネットワークは、Voltage Divider ネットワーク。
分圧器は、大きな電圧を小さな電圧に変える回路です。これは、直列に接続された抵抗を使用して行われます。出力は入力の一部になります。出力電圧は、駆動する負荷の抵抗に依存します。
分圧回路がどのように機能するかを見てみましょう。次の図は、単純な分圧器ネットワークの例です。
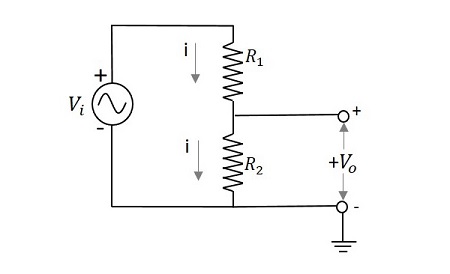
出力電圧の式を引こうとすると、
$$ V_ {i} = i \ left(R_ {1} + R_ {2} \ right)$$
$$ i = \ frac {V- {i}} {\ left(R_ {1} + R_ {2} \ right)} $$
$$ V_ {0} = i \:R_ {2} \ rightarrow \:i \:= \ frac {V_ {0}} {R_ {2}} $$
両方を比較すると、
$$ \ frac {V_ {0}} {R_ {2}} = \ frac {V_ {i}} {\ left(R_1 + R_ {2} \ right)} $$
$$ V_ {0} = \ frac {V_ {i}} {\ left(R_1 + R_ {2} \ right)} R_ {2} $$
出力電圧の値を求める式です。したがって、出力電圧はネットワーク内の抵抗の抵抗値に応じて分割されます。異なる出力電圧の異なる割合を持つために、より多くの抵抗が追加されます。
分圧器についてもっと理解するために問題の例を挙げましょう。
例
2つの直列抵抗2kΩと5kΩを使用して、入力電圧が10vのネットワークの出力電圧を計算します。
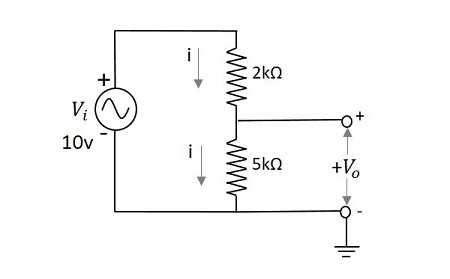
出力電圧$ V_ {0} $は次の式で与えられます。
$$ V_ {0} = \ frac {V_ {i}} {\ left(R_1 + R_ {2} \ right)} R_ {2} $$
$$ = \ frac {10} {\ left(2 + 5 \ right)k \ Omega} 5k \ Omega $$
$$ = \ frac {10} {7} \ times 5 = \ frac {50} {7} $$
$$ = 7.142v $$
上記の問題の出力電圧$ V_0 $は7.14vです