電子回路-整流器
AC電源をDC電源に変換する必要が生じたときはいつでも、整流回路が助けになります。単純なPN接合ダイオードが整流器として機能します。ダイオードの順方向バイアスと逆方向バイアスの条件により、整流が行われます。
整流
交流には、その状態を連続的に変化させる性質があります。これは、交流が示される正弦波を観察することで理解できます。正の方向に上昇し、正のピーク値になり、そこから通常に減少し、再び負の部分になり、負のピークに達し、再び通常に戻って続行します。
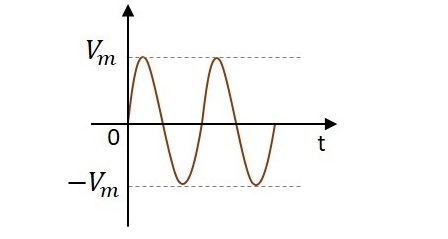
波の形成の旅の間に、私たちは波が正と負の方向に進むのを観察することができます。実際には完全に変化するため、名前は交流です。
しかし、整流の過程で、この交流は直流DCに変化します。それまで正と負の両方向に流れる波は、DCに変換すると正の方向にのみ方向が制限されます。したがって、下の図のように、電流は正の方向にのみ流れることができ、負の方向に抵抗されます。

整流を行う回路は、 Rectifier circuit。ダイオードは、整流回路を構築するための整流器として使用されます。
整流回路の種類
整流回路には、出力に応じて2つの主要なタイプがあります。彼らです
- 半波整流器
- 全波整流器
半波整流回路は入力電源の正の半サイクルのみを整流しますが、全波整流回路は入力電源の正と負の両方の半サイクルを整流します。
半波整流器
名前の半波整流器自体は、 rectification のためだけに行われます halfサイクルの。AC信号は、使用法に応じてステップアップまたはステップダウンする入力トランスを介して供給されます。ほとんどの場合、入力電圧を下げるために、整流回路には降圧トランスが使用されます。
トランスに与えられた入力信号は、整流器として機能するPN接合ダイオードを通過します。このダイオードは、入力の正の半サイクルの間だけ、AC電圧を脈動DCに変換します。回路の最後に負荷抵抗が接続されています。下の図は、半波整流器の回路を示しています。
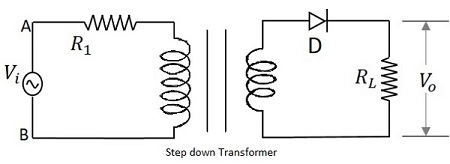
HWRの動作
T入力信号は変圧器に与えられ、電圧レベルを下げます。トランスからの出力は、整流器として機能するダイオードに与えられます。このダイオードは、入力信号の正の半サイクルでオン(導通)します。したがって、回路に電流が流れ、負荷抵抗の両端で電圧降下が発生します。ダイオードは負の半サイクルでオフ(導通しない)になるため、負の半サイクルの出力は$ i_ {D} = 0 $および$ V_ {o} = 0 $になります。
したがって、出力は入力電圧の正の半サイクルの間のみ存在します(逆リーク電流は無視します)。この出力は脈動し、負荷抵抗の両端で発生します。
HWRの波形
入力波形と出力波形は次の図のようになります。
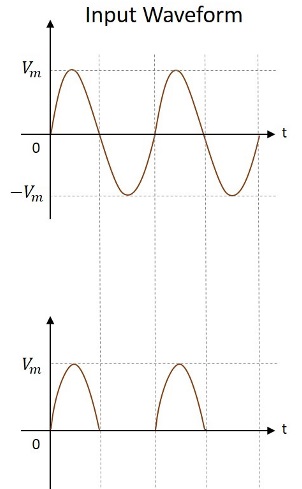
したがって、半波整流器の出力は脈流DCです。半波整流器の出力から得られるいくつかの値を理解することにより、上記の回路を分析してみましょう。
半波整流器の分析
半波整流回路を解析するために、入力電圧の式を考えてみましょう。
$$ v_ {i} = V_ {m} \ sin \ omega t $$
$ V_ {m} $は、供給電圧の最大値です。
ダイオードが理想的であると仮定しましょう。
- 順方向、つまりオン状態の抵抗は$ R_f $です。
- 逆方向、つまりオフ状態の抵抗は$ R_r $です。
現在 i ダイオードまたは負荷抵抗では$ R_L $は次の式で与えられます。
$ i = I_m \ sin \ omega t \ quad for \ quad 0 \ leq \ omega t \ leq 2 \ pi $
$ i = 0 \ quad \ quad \ quad \ quad for \ quad \ pi \ leq \ omega t \ leq 2 \ pi $
どこ
$$ I_m = \ frac {V_m} {R_f + R_L} $$
DC出力電流
平均電流$ I_ {dc} $は次の式で与えられます。
$$ I_ {dc} = \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i \:d \ left(\ omega t \ right)$$
$$ = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} I_m \ sin \ omega t \:d \ left(\ omega t \ right)+ \ int_ {0} ^ {2 \ pi} 0 \:d \ left(\ omega t \ right)\ right] $$
$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {-\ cos \ omega t \ right \} _ {0} ^ {\ pi} \ right] $$
$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {+ 1- \ left(-1 \ right)\ right \} \ right] = \ frac {I_m} {\ pi} = 0.318 I_m $$
$ I_m $の値を代入すると、次のようになります。
$$ I_ {dc} = \ frac {V_m} {\ pi \ left(R_f + R_L \ right)} $$
$ R_L >> R_f $の場合、
$$ I_ {dc} = \ frac {V_m} {\ pi R_L} = 0.318 \ frac {V_m} {R_L} $$
DC出力電圧
DC出力電圧は次の式で与えられます。
$$ V_ {dc} = I_ {dc} \ times R_L = \ frac {I_m} {\ pi} \ times R_L $$
$$ = \ frac {V_m \ times R_L} {\ pi \ left(R_f + R_L \ right)} = \ frac {V_m} {\ pi \ left \ {1+ \ left(R_f / R_L \ right)\ right \}} $$
$ R_L >> R_f $の場合、
$$ V_ {dc} = \ frac {V_m} {\ pi} = 0.318 V_m $$
RMS電流と電圧
RMS電流の値は次の式で与えられます。
$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i ^ {2} d \ left(\ omega t \ right)\ right] ^ {\ frac {1} {2}} $$
$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} I_ {m} ^ {2} \ sin ^ {2} \ omega t \: d \ left(\ omega t \ right)+ \ frac {1} {2 \ pi} \ int _ {\ pi} ^ {2 \ pi} 0 \:d \ left(\ omega t \ right)\ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {2 \ pi} \ int_ {0} ^ {\ pi} \ left(\ frac {1- \ cos 2 \ omega t} {2 } \ right)d \ left(\ omega t \ right)\ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ left(\ omega t \ right)-\ frac {\ sin 2 \ omega t} {2} \ right \} _ {0} ^ {\ pi} \ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ pi --0- \ frac {\ sin 2 \ pi} {2} + \ sin 0 \ right \} \ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ right] ^ {\ frac {1} {2}} = \ frac {I_m} {2} $$
$$ = \ frac {V_m} {2 \ left(R_f + R_L \ right)} $$
負荷両端のRMS電圧は
$$ V_ {rms} = I_ {rms} \ times R_L = \ frac {V_m \ times R_L} {2 \ left(R_f + R_L \ right)} $$
$$ = \ frac {V_m} {2 \ left \ {1+ \ left(R_f / R_L \ right)\ right \}} $$
$ R_L >> R_f $の場合、
$$ V_ {rms} = \ frac {V_m} {2} $$
整流器の効率
どの回路も、より良い出力を得るために効率的に動作する必要があります。半波整流器の効率を計算するには、入力電力に対する出力電力の比率を考慮する必要があります。
整流器の効率は次のように定義されます。
$$ \ eta = \ frac {dcpower \:\:配信\:\:to \:\:\:\:load} {acinput \:\:power \:\:from \:\:transformer \:\ :secondary} = \ frac {P_ {ac}} {P_ {dc}} $$
今
$$ P_ {dc} = \ left({I_ {dc}} \ right)^ 2 \ times R_L = \ frac {I_m R_L} {\ pi ^ 2} $$
さらに
$$ P_ {ac} = P_a + P_r $$
どこ
$ P_a = power \:dissipated \:at \:the \:junction \:of \:diode $
$$ = I_ {rms} ^ {2} \ times R_f = \ frac {I_ {m} ^ {2}} {4} \ times R_f $$
そして
$$ P_r = power \:dissipated \:in \:the \:load \:resistance $$
$$ = I_ {rms} ^ {2} \ times R_L = \ frac {I_ {m} ^ {2}} {4} \ times R_L $$
$$ P_ {ac} = \ frac {I_ {m} ^ {2}} {4} \ times R_f + \ frac {I_ {m} ^ {2}} {4} \ times R_L = \ frac {I_ {m } ^ {2}} {4} \ left(R_f + R_L \ right)$$
$ P_ {ac} $と$ P_ {dc} $の両方の式から、次のように書くことができます。
$$ \ eta = \ frac {I_ {m} ^ {2} R_L / \ pi ^ 2} {I_ {m} ^ {2} \ left(R_f + R_L \ right)/ 4} = \ frac {4} {\ pi ^ 2} \ frac {R_L} {\ left(R_f + R_L \ right)} $$
$$ = \ frac {4} {\ pi ^ 2} \ frac {1} {\ left \ {1+ \ left(R_f / R_L \ right)\ right \}} = \ frac {0.406} {\ left \ {1+ \ left(R_f / R_L \ right)\ right \}} $$
整流器の効率のパーセンテージ
$$ \ eta = \ frac {40.6} {\ lbrace1 + \ lgroup \:R_ {f} / R_ {L} \ rgroup \ rbrace} $$
理論的には、半波整流器の整流器効率の最大値は、$ R_ {f} / R_ {L} = 0 $の場合に40.6%です。
さらに、効率は以下の方法で計算することができる。
$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} = \ frac {\ left(I_ {dc} \ right)^ 2R_L} {\ left(I_ {rms} \ right)^ 2R_L} = \ frac {\ left(V_ {dc} / R_L \ right)^ 2R_L} {\ left(V_ {rms} / R_L \ right)^ 2R_L} = \ frac {\ left(V_ {dc} \ right)^ 2} {\ left(V_ {rms} \ right)^ 2} $$
$$ = \ frac {\ left(V_m / \ pi \ right)^ 2} {\ left(V_m / 2 \ right)^ 2} = \ frac {4} {\ pi ^ 2} = 0.406 $$
$$ = 40.6 \%$$
リップルファクター
整流された出力には、リップルの形で、その中に存在するAC成分がいくらか含まれています。これは、半波整流器の出力波形を観察することで理解できます。純粋なDCを取得するには、このコンポーネントについてのアイデアが必要です。
リップル係数は、整流された出力のうねりを示します。それはによって示されますy。これは、電圧または電流のAC成分の実効値と直接値または平均値の比率として定義できます。
$$ \ gamma = \ frac {ripple \:電圧} {dc \:電圧} = \ frac {rms \:value \:of \:accomponent} {dcvalue \:of \:wave} = \ frac {\ left( V_r \ right)_ {rms}} {v_ {dc}} $$
ここに、
$$ \ left(V_r \ right)_ {rms} = \ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}} $$
したがって、
$$ \ gamma = \ frac {\ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}}} {V_ {dc}} = \ sqrt {\ left(\ frac {V_ {rms} } {V_ {dc}} \ right)^ 2-1} $$
さて、
$$ V_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} V_ {m} ^ {2} \ sin ^ 2 \ omega t \:d \左(\ omega t \ right)\ right] ^ {\ frac {1} {2}} $$
$$ = V_m \ left [\ frac {1} {4 \ pi} \ int_ {0} ^ {\ pi} \ left(1- \ cos2 \:\ omega t \ right)d \ left(\ omega t \ right)\ right] ^ {\ frac {1} {2}} = \ frac {V_m} {2} $$
$$ V_ {dc} = V_ {av} = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} V_m \ sin \ omega t \:d \ left(\ omega t \ right)+ \ int_ {0} ^ {2 \ pi} 0.d \ left(\ omega t \ right)\ right] $$
$$ = \ frac {V_m} {2 \ pi} \ left [-\ cos \ omega t \ right] _ {0} ^ {\ pi} = \ frac {V_m} {\ pi} $$
$$ \ gamma = \ sqrt {\ left [\ left \ {\ frac {\ left(V_m / 2 \ right)} {\ left(V_m / \ pi \ right)} \ right \} ^ 2-1 \ right ]} = \ sqrt {\ left \ {\ left(\ frac {\ pi} {2} \ right)^ 2-1 \ right \}} = 1.21 $$
リップル係数は次のようにも定義されます。
$$ \ gamma = \ frac {\ left(I_r \ right)_ {rms}} {I_ {dc}} $$
半波整流器に存在するリップル係数の値は1.21であるため、出力に存在するACの量はDC電圧の$ 121 \%$であることを意味します
規制
負荷を流れる電流は、負荷抵抗によって異なる場合があります。しかし、そのような状態でも、その負荷抵抗の両端にかかる出力電圧は一定であると予想されます。したがって、さまざまな負荷条件でも電圧を調整する必要があります。
DC負荷電流の変化に伴うDC出力電圧の変化は、次のように定義されます。 Regulation。規制率は次のように計算されます。
$$ Percentage \:regulation = \ frac {V_ {no \:load} -V_ {full \:load}} {V_ {full \:load}} \ times 100 \%$$
規制の割合が低いほど、電源は良好になります。理想的な電源のレギュレーションはゼロパーセントです。
変圧器利用率
整流回路で負荷に供給されるDC電力は、回路で使用される変圧器の定格を決定します。
したがって、変圧器の使用率は次のように定義されます。
$$ TUF = \ frac {dcpower \:to \:be \:delivered \:to \:the \:load} {acrating \:of \:the \:transformer \:secondary} $$
$$ = \ frac {P_ {dc}} {P_ {ac \ left(評価\ right)}} $$
変圧器の理論によれば、二次側の定格電圧は
$$ V_m / \ sqrt {2} $$
それを流れる実際のRMS電圧は
$$ I_m / 2 $$
したがって、
$$ TUF = \ frac {\ left(I_m / \ pi \ right)^ 2 \ times R_L} {\ left(V_m / \ sqrt {2} \ right)\ times \ left(I_m / 2 \ right)} $ $
だが
$$ V_m = I_m \ left(R_f + R_L \ right)$$
したがって、
$$ TUF = \ frac {\ left(I_m / \ pi \ right)^ 2 \ times R_L} {\ left \ {I_m \ left(R_f + R_L \ right)/ \ sqrt {2} \ right \} \ times \ left(I_m / 2 \ right)} $$
$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} \ times \ frac {R_L} {\ left(R_f + R_L \ right)} $$
$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} = 0.287 $$
ピーク逆電圧
逆バイアスで接続されている場合、ダイオードは制御されたレベルの電圧で動作する必要があります。その安全電圧を超えると、ダイオードが損傷します。したがって、その最大電圧について知ることは非常に重要です。
ダイオードが破壊されることなく耐えることができる最大逆電圧は、 Peak Inverse Voltage。要するに、PIV。
ここで、PIVはVmに他なりません。
フォームファクタ
これは、波形上のすべてのポイントの絶対値の数学的平均として理解できます。ザ・form factor平均値に対するRMS値の比率として定義されます。それはによって示されますF。
$$ F = \ frac {rms \:value} {average \:value} = \ frac {I_m / 2} {I_m / \ pi} = \ frac {0.5I_m} {0.318I_m} = 1.57 $$
ピークファクター
リップルのピークの値は、整流がどれほど効果的であるかを知るために考慮する必要があります。ピークファクターの値も重要な考慮事項です。Peak factor RMS値に対するピーク値の比率として定義されます。
したがって、
$$ピーク係数= \ frac {Peak \:value} {rms \:value} = \ frac {V_m} {V_m / 2} = 2 $$
これらはすべて、整流器について研究する際に考慮すべき重要なパラメータです。