電子回路-クイックガイド
エレクトロニクスには、さまざまな目的に役立つさまざまなコンポーネントがあります。用途に応じて、さまざまな種類の回路で使用されるさまざまな要素があります。
電子部品
壁を構成するレンガと同様に、コンポーネントは回路の基本的なレンガです。AComponent アイデアの発展に貢献する基本的な要素です circuit 実行のため。
各コンポーネントにはいくつかの基本的なプロパティがあり、コンポーネントはそれに応じて動作します。目的の回路の構築にそれらを使用することは、開発者のモットーに依存します。次の画像は、さまざまな電子回路で使用される電子部品のいくつかの例を示しています。

アイデアを集めるために、コンポーネントのタイプを見てみましょう。彼らはどちらかActive Components または Passive Components。
アクティブコンポーネント
アクティブコンポーネントは、外部エネルギーを提供するときに伝導するコンポーネントです。
アクティブコンポーネントは、電圧または電流の形でエネルギーを生成します。
Examples −ダイオード、トランジスタ、トランスなど。
受動部品
受動部品とは、接続されると動作を開始する部品です。それらの操作に外部エネルギーは必要ありません。
受動部品は、電圧または電流の形でエネルギーを貯蔵および維持します。
Examples −抵抗、コンデンサ、インダクタなど。
別の分類もあります Linear そして Non-Linear 要素。
線形コンポーネント
線形要素またはコンポーネントは、電流と電圧の間に線形関係があるものです。
線形要素のパラメータは、電流と電圧に関して変更されません。
Examples −ダイオード、トランジスタ、トランスなど。
非線形コンポーネント
非線形要素またはコンポーネントは、電流と電圧の間に非線形の関係があるものです。
非線形要素のパラメータは、電流と電圧に関して変更されます。
Examples −抵抗、コンデンサ、インダクタなど。
これらはさまざまな目的を目的としたコンポーネントであり、それらが構築された優先タスクを完全に実行できます。異なるコンポーネントのこのような組み合わせは、Circuit。
電子回路
特定の方法で目的に接続すると、特定の数のコンポーネントが circuit。回路は、さまざまなコンポーネントのネットワークです。回路にはさまざまな種類があります。
次の画像は、さまざまな種類の電子回路を示しています。ボード上に接続された電子回路のグループであるプリント回路基板を示しています。

電子回路は、その動作、接続、構造などに応じて、さまざまなカテゴリに分類できます。電子回路の種類について詳しく説明します。
アクティブ回路
アクティブコンポーネントを使用して構築された回路は、 Active Circuit。
通常、回路がより多くの電力を抽出して負荷に供給する電源が含まれています。
追加の電力が出力に追加されるため、出力電力は常に適用される入力電力よりも大きくなります。
パワーゲインは常に1より大きくなります。
受動回路
受動部品を使用して構築された回路は、 Passive Circuit。
電源が入っていても、回路は電力を引き出しません。
追加電力は出力に追加されないため、出力電力は常に適用される入力電力よりも少なくなります。
電力利得は常に1未満になります。
電子回路は次のように分類することもできます Analog, Digital、または Mixed。
アナログ回路
アナログ回路は、線形成分を含む回路にすることができます。したがって、それは線形回路です。
アナログ回路には、連続した電圧範囲のアナログ信号入力があります。
デジタル回路
デジタル回路は、非線形成分を含む回路にすることができます。したがって、それは非線形回路です。
デジタル信号のみを処理できます。
デジタル回路には、離散値であるデジタル信号入力があります。
ミックスドシグナル回路
ミックスドシグナル回路は、線形成分と非線形成分の両方を含む回路にすることができます。したがって、それはミックスドシグナル回路と呼ばれます。
これらの回路は、入力を処理するためのマイクロプロセッサを備えたアナログ回路で構成されています。
接続の種類に応じて、回路は次のいずれかに分類できます。 Series Circuit または Parallel Circuit。直列回路は、直列に接続された回路であり、parallel circuit コンポーネントが並列に接続されているものです。
電子部品についての基本的な考え方がわかったところで、次に進んで、さまざまなアプリケーション向けのより良い回路を構築するのに役立つそれらの目的について説明します。電子回路の目的(処理、送信、受信、分析)が何であれ、プロセスは信号の形で実行されます。次の章では、電子回路に存在する信号と信号の種類について説明します。
A Signal「データが生成されたソースに存在するデータに関する情報を提供する表現」として理解できます。これは通常、時間によって変化します。したがって、信号はsource of energy which transmits some information。これは簡単にグラフで表すことができます。
例
- アラームは時間だという合図を出します。
- 炊飯器の笛は、食品が調理されたことを確認します。
- 赤信号は危険を示します。
- 信号はあなたの動きを示します。
- 電話が鳴り、電話がかかってきます。
信号は、何らかの情報を伝達する任意のタイプにすることができます。電子機器から生成されるこの信号は、Electronic Signal または Electrical Signal。これらは一般的に時変です。
信号の種類
信号は、その特性に応じて、アナログまたはデジタルのいずれかに分類できます。次の画像に示すように、アナログ信号とデジタル信号はさらに分類できます。
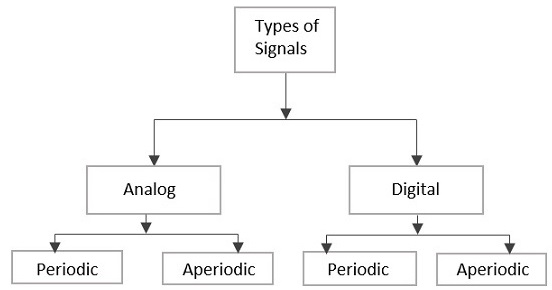
アナログ信号
時間変化する量を表す連続的な時間変化する信号は、次のように呼ぶことができます。 Analog Signal。この信号は、それを表す量の瞬時値に応じて、時間に対して変化し続けます。
デジタル信号
である信号 discrete 自然の中で、またはどちらですか non-continuous 形では、 Digital signal。この信号には、個別に示される個々の値があります。これらは、特定の時点で導出されたかのように、以前の値に基づいていません。
周期信号と非周期信号
一定期間にわたってそのパターンを繰り返すアナログまたはデジタル信号は、 Periodic Signal。この信号はそのパターンが繰り返し継続されており、推測や計算が容易です。
一定期間にわたってそのパターンを繰り返さないアナログまたはデジタル信号は、次のように呼ばれます。 Aperiodic Signal。この信号のパターンは継続されますが、パターンは繰り返されず、想定や計算が簡単ではありません。
信号と表記
間で Periodic Signals、最も一般的に使用される信号は、正弦波、余弦波、三角波、方形波、方形波、鋸歯状波形、パルス波形、パルス列などです。これらの波形を見てみましょう。
ユニットステップ信号
単位ステップ信号は、原点からX軸上の1単位までの1単位の値を持ちます。これは主にテスト信号として使用されます。単位ステップ信号の画像を以下に示します。
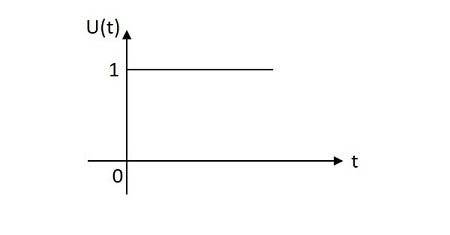
単位ステップ関数は次のように表されます。 $u\left ( t \right )$。それは次のように定義されます-
$$ u \ left(t \ right)= \ left \ {\ begin {matrix} 1&t \ geq 0 \\ 0&t <0 \ end {matrix} \ right。$$
ユニットインパルス信号
単位インパルス信号は、その原点で1単位の値を持ちます。その面積は1ユニットです。単位インパルス信号の画像を以下に示します。
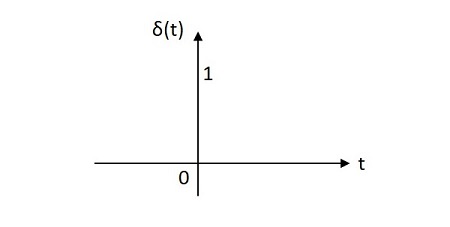
単位インパルス関数はで表されます ẟ(t)。それは次のように定義されています
$$\delta \left ( t \right )=\left\{\begin{matrix} \infty \:\:if \:\:t=0\\0 \:\:if \:\:t\neq 0\end{matrix}\right.$$
$$\int_{-\infty }^{\infty }\delta \left ( t \right )d\left ( t \right )=1$$
$$\int_{-\infty }^{t }\delta \left ( t \right )d\left ( t \right )=u\left ( t \right )$$
$$\delta \left ( t \right )=\frac{du\left ( t \right )}{d\left ( t \right )} $$
ユニットランプ信号
ユニットランプ信号の値は、原点から指数関数的に増加します。ユニットランプ信号の画像を以下に示します。
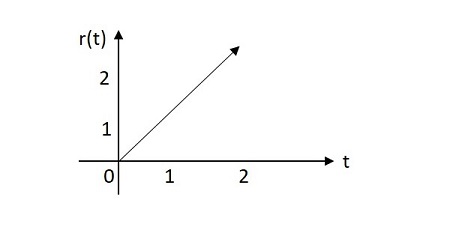
ユニットランプ関数は次のように表されます。 u(t)。それは次のように定義されます-
$$\int_{0}^{t}u\left ( t \right ) d\left ( t \right )=\int_{0}^{t} 1 dt =t=r\left ( t \right )$$
$$u\left ( t \right )=\frac{dr\left ( t \right )}{dt}$$
単位放物線信号
単位放物線信号の値は、原点で放物線のように変化します。単位放物線信号の画像を以下に示します。
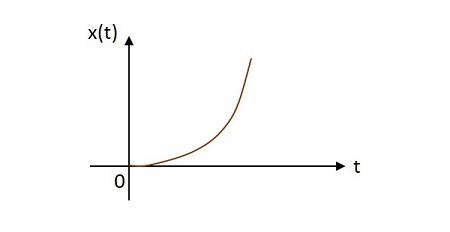
単位放物関数はで表されます $u\left ( t \right )$。それは次のように定義されます-
$$\int_{0}^{t}\int_{0}^{t}u\left ( t \right )dtdt=\int_{0}^{t}r\left ( t \right )dt=\int_{0}^{t} t.dt=\frac{t^{2}}{2}dt=x\left ( t \right )$$
$$r\left ( t \right )=\frac{dx\left ( t \right )}{dt}$$
$$u\left ( t \right )=\frac{d^{2}x\left ( t \right )}{dt^{2}}$$
符号関数
符号関数の値は、原点から正と負の両方の平面に均等に分布しています。シグナム関数の画像を以下に示します。
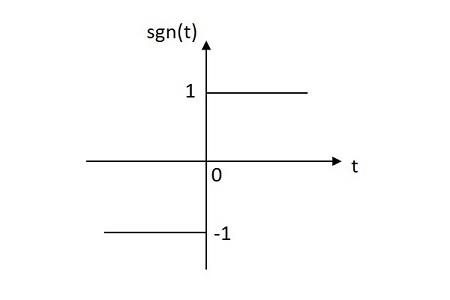
符号関数はで表されます sgn(t)。それは次のように定義されています
$$ sgn \ left(t \ right)= \ left \ {\ begin {matrix} 1 \:\:for \:\:t \ geq 0 \\-1 \:\:for \:\:t <0 \ end {matrix} \ right。$$
$$sgn\left ( t \right )=2u\left ( t \right ) -1$$
指数信号
指数信号の値は、原点から指数関数的に変化します。指数関数は-の形式です
$$x\left ( t \right ) =e^{\alpha t}$$
指数の形は次のように定義できます。 $\alpha$。この機能は3つのケースで理解できます
Case 1 −
場合 $\alpha = 0\rightarrow x\left ( t \right )=e^{0}=1$
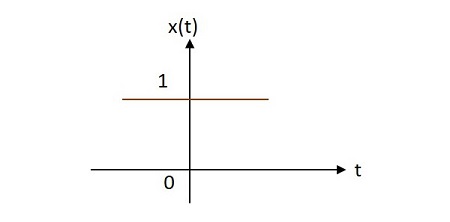
Case 2 −
$ \ alpha <0 $の場合、 $x\left ( t \right )=e^{\alpha t}$ どこ $\alpha$負です。この形はdecaying exponential。
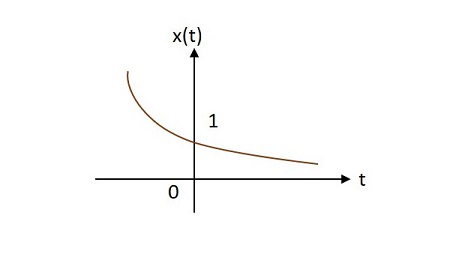
Case 3 −
場合 $\alpha > 0$ その後 $x\left ( t \right )=e^{\alpha t}$ どこ $\alpha$ポジティブです。この形はraising exponential。
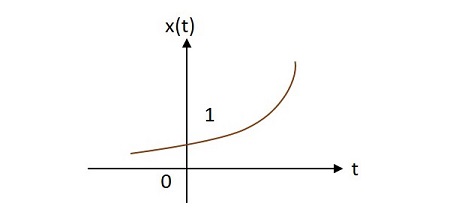
長方形信号
長方形の信号の値は、原点から正と負の両方の平面に長方形の形で分布しています。矩形信号の画像を以下に示します。
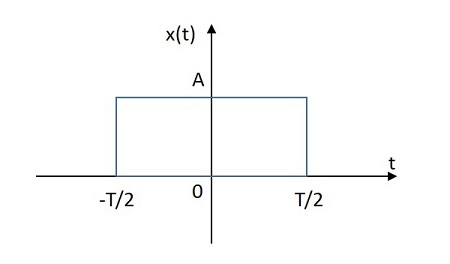
矩形関数はで表されます $x\left ( t \right )$。それは次のように定義されています
$$x\left ( t \right )=A \:rect\left [ \frac{t}{T} \right ]$$
三角波信号
長方形の信号の値は、原点から正と負の両方の平面に三角形で分布しています。三角信号の画像を以下に示します。
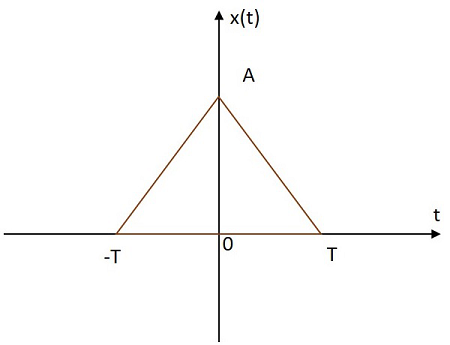
三角関数はで表されます$x\left ( t \right )$。それは次のように定義されています
$$x\left ( t \right )=A \left [ 1-\frac{\left | t \right |}{T} \right ]$$
正弦波信号
正弦波信号の値は、その原点から正弦波的に変化します。正弦波信号の画像を以下に示します。
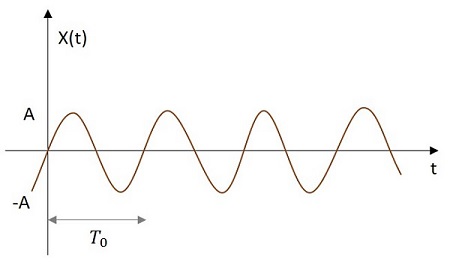
正弦関数はx(t)で表されます。それは次のように定義されます-
$$x\left ( t \right )=A \cos \left ( w_{0} t\pm \phi \right )$$
または
$$x\left ( t \right )=A sin\left ( w_{0}t\pm \phi \right )$$
どこ $T_{0}=\frac{2 \pi}{w_{0}}$
Sinc関数
Sinc信号の値は、以下の式のように特定の関係に従って変化します。原点で最大値を持ち、遠ざかるにつれて減少し続けます。Sinc関数信号の画像を以下に示します。
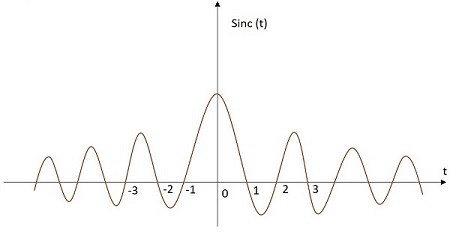
Sinc関数は次のように表されます。 sinc(t)。それは次のように定義されます-
$$sinc\left ( t \right )=\frac{sin\left ( \pi t \right )}{\pi t}$$
したがって、これらは、電子通信の分野で主に遭遇するさまざまな信号です。すべての信号を数式で定義して、信号分析を容易にすることができます。
前述のように、各信号には特定の波形があります。波の形状により、信号に存在する内容が変わる可能性があります。とにかく、特定の回路に対して波を変更するかどうかは、設計エンジニアが決定します。しかし、波の形を変えるために、さらなるユニットで議論されるいくつかのテクニックがあります
シグナルは、 Wave。すべての波は、グラフで表されるときに特定の形状を持ちます。この形状は、正弦波、正方形、三角形など、期間によって異なるさまざまなタイプにすることができます。または、期間を無視してランダムな形状にすることもできます。
波形整形の種類
波形整形には主に2つのタイプがあります。彼らは-
- 線形波形整形
- 非線形波形整形
線形波形整形
抵抗、コンデンサ、インダクタなどの線形要素を使用して、この線形波形で信号を整形します。正弦波入力には正弦波出力があるため、線形波形を理解するために非正弦波入力がより顕著に使用されます。
Filtering 不要な信号を減衰させるプロセス、または特定の信号の周波数成分の選択された部分を再生するプロセスです。
フィルター
信号を整形する過程で、信号の一部が不要だと感じた場合は、フィルター回路を使用してそれらを遮断することができます。 A Filter is a circuit that can remove unwanted portions of a signal at its input。信号の強度が低下するプロセスは、次のようにも呼ばれます。Attenuation。
フィルタリング技術に役立つコンポーネントはほとんどありません。
A Capacitor にプロパティを持っています allow AC とに block DC
アン Inductor にプロパティを持っています allow DC だが blocks AC。
これらのプロパティを使用して、これらの2つのコンポーネントは、特にブロックまたは許可するために使用されます AC または DC。フィルタは、これらのプロパティに応じて設計できます。
フィルタには主に4つのタイプがあります-
- ローパスフィルタ
- ハイパスフィルタ
- バンドパスフィルター
- バンドストップフィルター
これらのタイプのフィルターについて詳しく説明します。
ローパスフィルタ
指定された値を下回る周波数のセットを可能にするフィルター回路は、 Low pass filter。このフィルターは低い周波数を通過させます。RCとRLを使用したローパスフィルタの回路図を以下に示します。
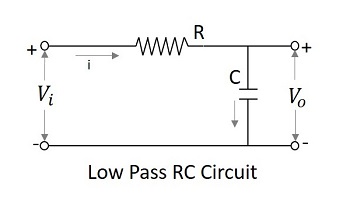
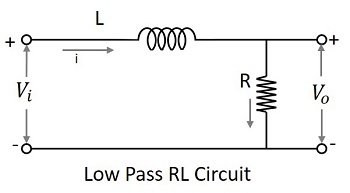
コンデンサーフィルターまたは RC フィルタとインダクタフィルタまたはRLフィルタは両方ともローパスフィルタとして機能します。
The RC filter−コンデンサがシャントに配置されると、コンデンサが許可するACが接地されます。これにより、すべての高周波成分が通過し、出力でDCが可能になります。
The RL filter−インダクタが直列に配置されているため、DCは出力に許可されます。インダクタは、出力で許可されていないACをブロックします。
ローパスフィルター(LPF)の記号は以下のとおりです。
周波数応答
実用的なフィルタの周波数応答は以下のとおりであり、電子部品の実用的な考慮事項を考慮しない場合の理想的なLPFの周波数応答は次のようになります。
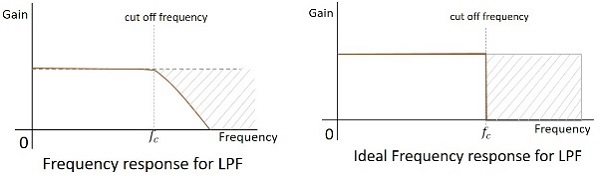
フィルタのカットオフ周波数は臨界周波数です $f_{c}$フィルタが信号を減衰(カット)することを目的としています。理想的なフィルターには完全なカットオフがありますが、実用的なフィルターにはいくつかの制限があります。
RLCフィルター
RCフィルターとRLフィルターについて知った後、より良い応答を得るためにこれら2つの回路を追加するのが良いだろうという考えを持っているかもしれません。次の図は、RLC回路がどのように見えるかを示しています。
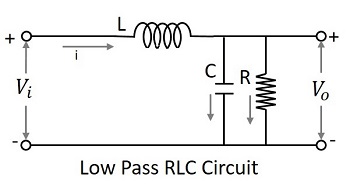
入力の信号は、ACをブロックしてDCを許可するインダクタを通過します。ここで、その出力はシャント内のコンデンサを再び通過します。これにより、信号に存在する残りのACコンポーネントが接地され、出力でDCが可能になります。したがって、出力には純粋なDCがあります。これは、両方よりも優れたローパス回路です。
ハイパスフィルタ
次の周波数のセットを可能にするフィルター回路 above a specified value と呼ぶことができます High pass filter。このフィルターはより高い周波数を通過させます。RCとRLを使用したハイパスフィルターの回路図を以下に示します。
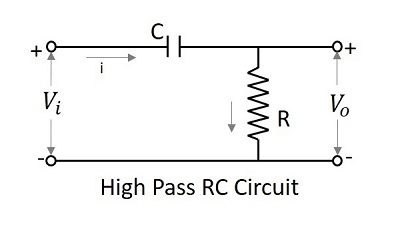
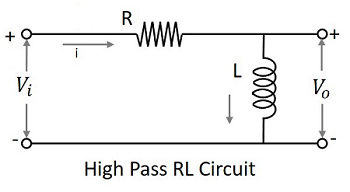
コンデンサーフィルターまたは RC フィルタとインダクタフィルタまたは RL フィルタは両方ともハイパスフィルタとして機能します。
RCフィルター
コンデンサは直列に配置されているため、DCコンポーネントをブロックし、ACコンポーネントを出力に許可します。したがって、高周波成分は抵抗の両端の出力に現れます。
RLフィルター
インダクタがシャントに配置されているため、DCを接地することができます。残りのACコンポーネントが出力に表示されます。ハイパスフィルター(HPF)の記号は以下のとおりです。
周波数応答
実用的なフィルターの周波数応答は以下のとおりであり、電子部品の実用的な考慮事項を考慮しない場合の理想的なHPFの周波数応答は次のようになります。
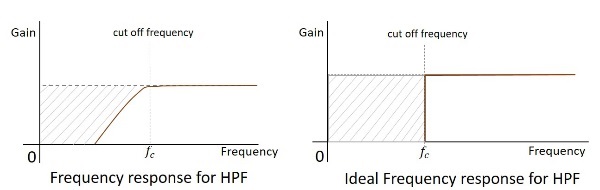
フィルタのカットオフ周波数は臨界周波数です $f_{c}$フィルタが信号を減衰(カット)することを目的としています。理想的なフィルターには完全なカットオフがありますが、実用的なフィルターにはいくつかの制限があります。
RLCフィルター
RCフィルターとRLフィルターについて知った後、より良い応答を得るためにこれら2つの回路を追加するのが良いだろうという考えを持っているかもしれません。次の図は、RLC回路がどのように見えるかを示しています。

入力の信号は、DCをブロックしてACを許可するコンデンサを通過します。ここで、その出力はシャントのインダクタを再び通過します。これにより、信号に存在する残りのDC成分が接地され、出力でACが可能になります。したがって、出力には純粋なACがあります。これは、両方よりも優れたハイパス回路です。
バンドパスフィルター
次の周波数のセットを可能にするフィルター回路 between two specified values と呼ぶことができます Band pass filter。このフィルターは周波数帯域を通過させます。
低周波数と高周波数のいくつかを削除する必要があるため、指定された周波数のセットを選択するには、HPFとLPFをカスケードしてBPFを取得する必要があります。これは、周波数応答曲線を観察しても簡単に理解できます。
バンドパスフィルターの回路図は以下のとおりです。
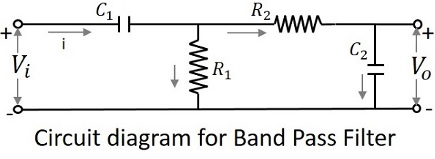
上記の回路は、RL回路またはRLC回路を使用して構築することもできます。上記はわかりやすくするために選んだRC回路です。
バンドパスフィルター(BPF)の記号は以下のとおりです。
周波数応答
実用的なフィルタの周波数応答は以下のとおりであり、電子部品の実用的な考慮事項を考慮しない場合の理想的なBPFの周波数応答は次のようになります。
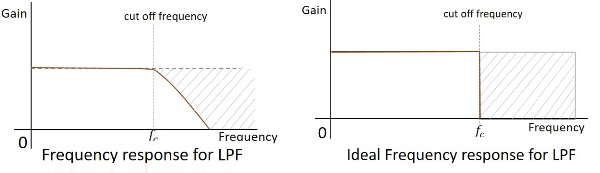
フィルタのカットオフ周波数は臨界周波数です $f_{c}$フィルタが信号を減衰(カット)することを目的としています。理想的なフィルターには完全なカットオフがありますが、実用的なフィルターにはいくつかの制限があります。
バンドストップフィルター
周波数のセットをブロックまたは減衰するフィルター回路 between two specified values と呼ぶことができます Band Stop filter。このフィルターは周波数帯域を拒否するため、次のように呼び出すこともできます。Band Reject Filter。
低周波数と高周波数のいくつかを排除する必要があるため、指定された周波数のセットを選択するには、LPFとHPFをカスケードしてBSFを取得する必要があります。これは、周波数応答曲線を観察しても簡単に理解できます。
バンドストップフィルタの回路図は以下のとおりです。
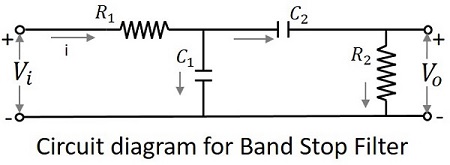
上記の回路は、RL回路またはRLC回路を使用して構築することもできます。上記はわかりやすくするために選んだRC回路です。
バンドストップフィルター(BSF)の記号は以下のとおりです。
周波数応答
実用的なフィルターの周波数応答は以下のとおりであり、電子部品の実用的な考慮事項を考慮しない場合の理想的なBSFの周波数応答は次のようになります。
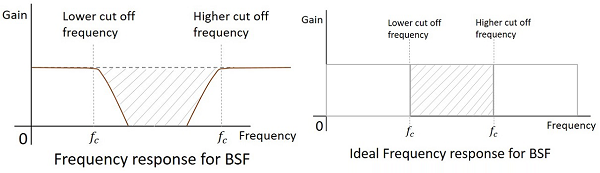
フィルタのカットオフ周波数は臨界周波数です $f_{c}$フィルタが信号を減衰(カット)することを目的としています。理想的なフィルターには完全なカットオフがありますが、実用的なフィルターにはいくつかの制限があります。
ローパスおよびハイパスフィルター回路は、多くのアプリケーションで特殊な回路として使用されます。ローパスフィルター(LPF)は、Integrator、一方、ハイパスフィルター(HPF)は Differentiator。これらの2つの数学関数は、多くのアプリケーションで電子技術者の労力を軽減するこれらの回路でのみ可能です。
積分器としてのローパスフィルター
低周波数では、容量性リアクタンスは無限大になる傾向があり、高周波数では、リアクタンスはゼロになります。したがって、低周波数では、LPFの出力は有限であり、高周波数では、出力はゼロです。これは、積分回路の場合と同じです。したがって、ローパスフィルターは次のように機能すると言えます。integrator。
LPFがインテグレータとして動作するため
$$\tau \gg T$$
どこ $\tau = RC$ 回路の時定数
その場合、Cの電圧変動は非常に小さくなります。
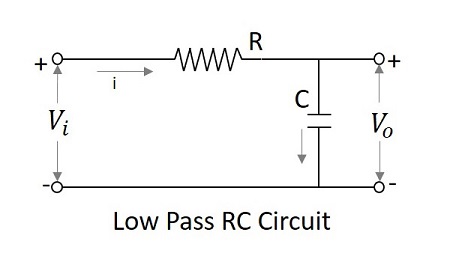
$$V_{i}=iR+\frac{1}{C} \int i \:dt$$
$$V_{i}\cong iR$$
$$Since \:\: \frac{1}{C} \int i \:dt \ll iR$$
$$i=\frac{V_{i}}{R}$$
$$ Since \:\: V_{0}=\frac{1}{C}\int i dt =\frac{1}{RC}\int V_{i}dt=\frac{1}{\tau }\int V_{i} dt$$
$$Output \propto \int input$$
したがって、時定数が大きいLPFは、入力の積分に比例する出力を生成します。
周波数応答
積分器として機能する場合の実用的なローパスフィルターの周波数応答は以下のとおりです。
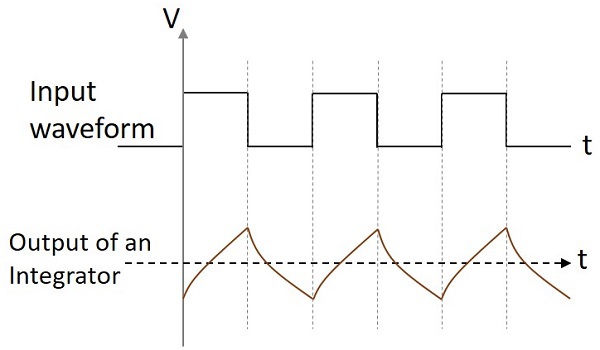
出力波形
積分回路に正弦波入力が与えられている場合、出力は余弦波になります。入力が方形波の場合、出力波形は形状が変化し、下図のようになります。
微分器としてのハイパスフィルター
低周波数では、微分器の出力はゼロですが、高周波数では、その出力は有限値になります。これは微分器の場合と同じです。したがって、ハイパスフィルターは微分器として動作すると言われています。
RC HPFの時定数が入力信号の時定数よりも非常に小さい場合、回路は微分器として動作します。その場合、Cの両端の電圧降下と比較すると、Rの両端の電圧降下は非常に小さくなります。
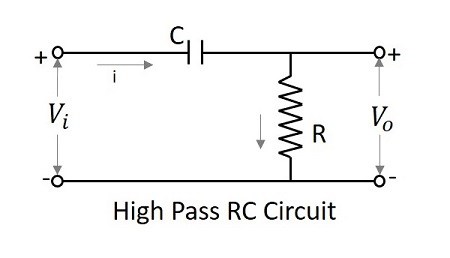
$$V_{i}=\frac{1}{C}\int i \:dt +iR$$
だが $iR=V_{0}$ 小さいです
$$since V_{i}=\frac{1}{C}\int i \:dt$$
$$i=\frac{V_{0}}{R}$$
$$Since \: V_{i} =\frac{1}{\tau }\int V_{0} \:dt$$
どこ $\tau =RC$ 回路の時定数。
両側で差別化、
$$\frac{dV_{i}}{dt}=\frac{V_0}{\tau }$$
$$V_{0}=\tau \frac{dV_{i}}{dt}$$
$$Since \:V_{0}\propto \frac{dV_{i}}{dt}$$
出力は入力信号の差動に比例します。
周波数応答
微分器として機能する場合の実用的なハイパスフィルターの周波数応答は以下のとおりです。
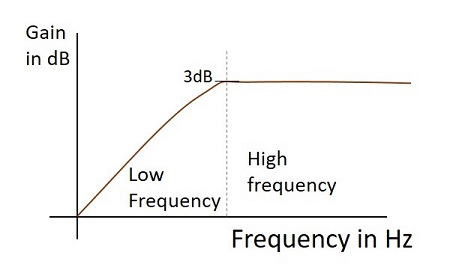
出力波形
微分回路に正弦波入力が与えられている場合、出力は余弦波になります。入力が方形波の場合、出力波形は形状が変化し、下図のようになります。
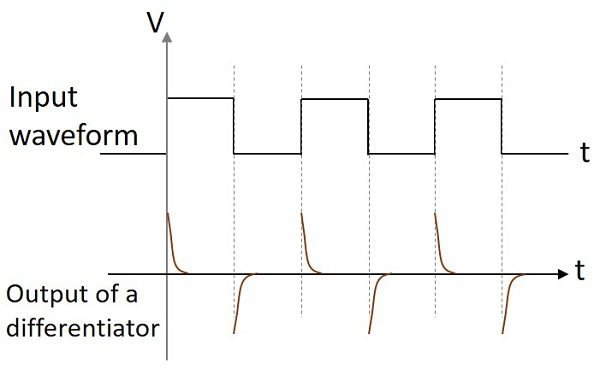
これらの2つの回路は、主にさまざまな電子アプリケーションで使用されます。微分回路は、印加される入力が着実に変化する傾向がある場合、一定の出力電圧を生成します。積分回路は、印加される入力電圧が一定の場合、着実に変化する出力電圧を生成します。
抵抗器とともに、次のような非線形要素 diodes必要な変更された出力を取得するために、非線形波形整形回路で使用されます。波の形状が減衰するか、波のDCレベルが非線形波形整形で変更されます。
非線形要素を使用して、正弦波入力から非正弦波出力波形を生成するプロセスは、次のように呼ばれます。 nonlinear wave shaping。
クリッパー回路
クリッパー回路は、 rejects the part 指定された入力波の allowing the remaining部分。決定されたカットオフ電圧より上または下の波の部分は、クリップオフまたはカットオフされます。
クリッピング回路は、抵抗やダイオードなどの線形要素と非線形要素で構成されていますが、コンデンサなどのエネルギー貯蔵要素は含まれていません。これらのクリッピング回路は、有利であるため、多くの用途があります。
クリッピング回路の主な利点は、振幅に存在する不要なノイズを排除することです。
これらは、クリッピングによって正弦波を方形波に変換できるため、方形波コンバーターとして機能します。
所望の波の振幅を一定レベルに維持することができます。
ダイオードクリッパーの中で、2つの主なタイプは次のとおりです。 positive そして negative clippers。次の2つの章では、これら2種類のバリカンについて説明します。
入力信号の正の部分を減衰させることを目的としたクリッパー回路は、 Positive Clipper。正ダイオードクリッパー回路には、以下のタイプがあります。
- ポジティブシリーズクリッパー
- ポジティブシリーズクリッパー $V_{r}$ (基準電圧)
- ネガティブシリーズクリッパー $V_{r}$
- ポジティブシャントクリッパー
- ポジティブシャントクリッパー $V_{r}$
- ネガティブ付きポジティブシャントクリッパー $V_{r}$
これらの各タイプについて詳しく説明します。
ポジティブシリーズクリッパー
ダイオードが入力信号に直列に接続され、波形の正の部分を減衰させるクリッパー回路は、次のように呼ばれます。 Positive Series Clipper。次の図は、正の直列クリッパーの回路図を表しています。

Positive Cycle of the Input−入力電圧が印加されると、入力の正のサイクルにより、回路内のポイントAがポイントBに対して正になります。これにより、ダイオードが逆バイアスされ、オープンスイッチのように動作します。したがって、負荷抵抗に電流が流れないため、負荷抵抗の両端の電圧はゼロになります。$V_{0}$ ゼロになります。
Negative Cycle of the Input−入力の負のサイクルにより、回路内のポイントAがポイントBに対して負になります。これにより、ダイオードが順方向にバイアスされるため、閉じたスイッチのように動作します。したがって、負荷抵抗の両端の電圧は、出力に完全に現れるため、印加された入力電圧に等しくなります。$V_{0}$。
波形
上の図では、波形を観察すると、正のピークの一部しかクリップされていないことがわかります。これは、V0の両端の電圧によるものです。しかし、理想的な出力はそうなることを意図していませんでした。次の図を見てみましょう。
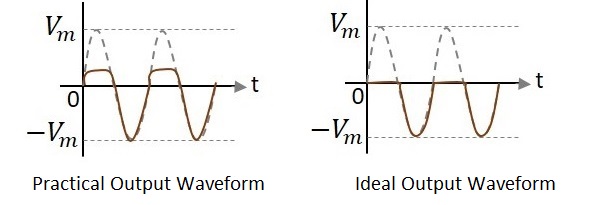
理想的な出力とは異なり、ダイオードの導通電圧が0.7vであるため、実際の出力には正のサイクルのビット部分が存在します。したがって、実際の出力波形と理想的な出力波形には違いがあります。
ポジティブシリーズクリッパー $V_{r}$
ダイオードが入力信号に直列に接続され、正の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の正の部分を減衰させるものは、次のように呼ばれます。 Positive Series Clipper with positive $V_{r}$。次の図は、印加された基準電圧が正の場合の正の直列クリッパーの回路図を表しています。
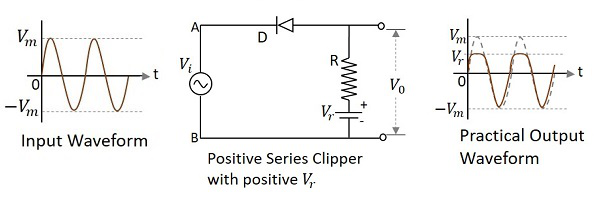
入力の正のサイクル中に、ダイオードは逆バイアスされ、基準電圧が出力に現れます。負のサイクルの間、ダイオードは順方向にバイアスされ、閉じたスイッチのように動作します。したがって、出力波形は上図のようになります。
ネガティブシリーズクリッパー $V_{r}$
ダイオードが入力信号に直列に接続され、負の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の正の部分を減衰させるものは、次のように呼ばれます。 Positive Series Clipper with negative $V_{r}$。次の図は、印加された基準電圧が負の場合の正の直列クリッパーの回路図を表しています。
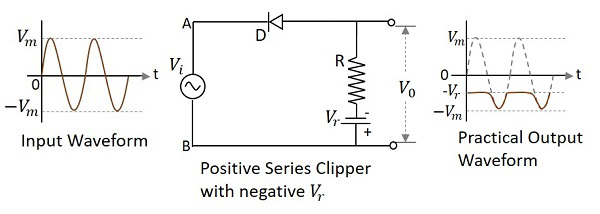
入力の正のサイクル中に、ダイオードは逆バイアスされ、基準電圧が出力に現れます。基準電圧が負であるため、一定の振幅を持つ同じ電圧が表示されます。負のサイクルの間、ダイオードは順方向にバイアスされ、閉じたスイッチのように動作します。したがって、基準電圧よりも大きい入力信号が出力に現れます。
ポジティブシャントクリッパー
ダイオードが入力信号にシャントで接続され、波形の正の部分を減衰させるクリッパー回路は、次のように呼ばれます。 Positive Shunt Clipper。次の図は、ポジティブシャントクリッパーの回路図を表しています。
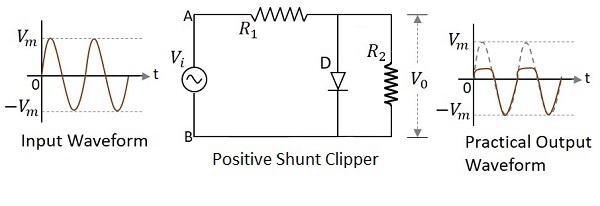
Positive Cycle of the Input−入力電圧が印加されると、入力の正のサイクルにより、回路内のA点がB点に対して正になります。これにより、ダイオードが順方向にバイアスされるため、閉じたスイッチのように動作します。したがって、負荷抵抗に電流が流れないため、負荷抵抗の両端の電圧はゼロになります。$V_{0}$ ゼロになります。
Negative Cycle of the Input−入力の負のサイクルにより、回路内のポイントAがポイントBに対して負になります。これにより、ダイオードが逆バイアスされ、オープンスイッチのように動作します。したがって、負荷抵抗の両端の電圧は、出力に完全に現れるため、印加された入力電圧に等しくなります。$V_{0}$。
波形
上の図では、波形を観察すると、正のピークの一部しかクリップされていないことがわかります。これは、両端の電圧によるものです$V_{0}$。しかし、理想的な出力はそうなることを意図していませんでした。次の図を見てみましょう。
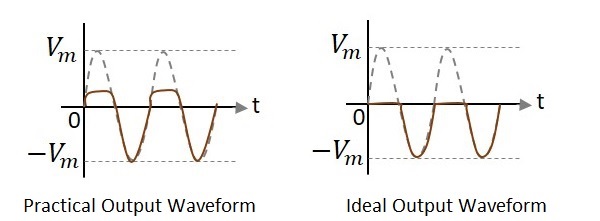
理想的な出力とは異なり、ダイオードの導通電圧が0.7vであるため、実際の出力には正のサイクルのビット部分が存在します。したがって、実際の出力波形と理想的な出力波形には違いがあります。
ポジティブシャントクリッパー $V_{r}$
ダイオードが入力信号にシャント接続され、正の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の正の部分を減衰させるものは、次のように呼ばれます。 Positive Shunt Clipper with positive $V_{r}$。次の図は、印加された基準電圧が正の場合の正のシャントクリッパーの回路図を表しています。
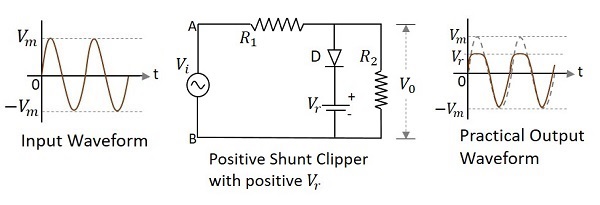
入力の正のサイクルの間、ダイオードは順方向にバイアスされ、基準電圧だけが出力に現れます。負のサイクルの間、ダイオードは逆バイアスされ、オープンスイッチとして動作します。入力全体が出力に表示されます。したがって、出力波形は上図のようになります。
ネガティブ付きポジティブシャントクリッパー $V_{r}$
ダイオードが入力信号にシャント接続され、負の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の正の部分を減衰させるものは、次のように呼ばれます。 Positive Shunt Clipper with negative $V_{r}$。
次の図は、印加された基準電圧が負の場合の正のシャントクリッパーの回路図を表しています。
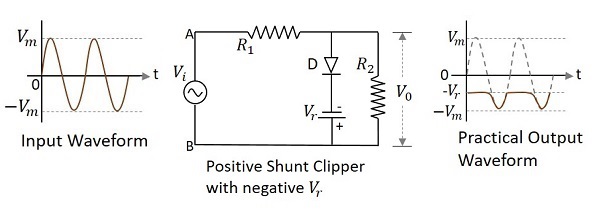
入力の正のサイクル中に、ダイオードは順方向にバイアスされ、基準電圧が出力に現れます。基準電圧が負であるため、一定の振幅を持つ同じ電圧が表示されます。負のサイクルの間、ダイオードは逆バイアスされ、オープンスイッチとして動作します。したがって、基準電圧よりも大きい入力信号が出力に現れます。
入力信号の負の部分を減衰させることを目的としたクリッパー回路は、 Negative Clipper。マイナスダイオードクリッパー回路には、以下のタイプがあります。
- ネガティブシリーズクリッパー
- ポジティブシリーズクリッパー $V_{r}$ (基準電圧)
- ネガティブシリーズクリッパーネガティブ付き $V_{r}$
- ネガティブシャントクリッパー
- ポジティブのネガティブシャントクリッパー $V_{r}$
- ネガティブシャントクリッパー $V_{r}$
これらの各タイプについて詳しく説明します。
ネガティブシリーズクリッパー
ダイオードが入力信号に直列に接続され、波形の負の部分を減衰させるクリッパー回路は、次のように呼ばれます。 Negative Series Clipper。次の図は、負の直列クリッパーの回路図を表しています。
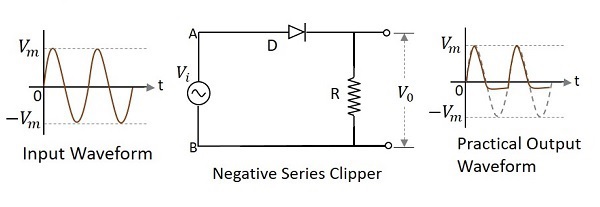
Positive Cycle of the Input−入力電圧が印加されると、入力の正のサイクルにより、回路内の点Aが点Bに対して正になります。これにより、ダイオードが順方向にバイアスされるため、閉じたスイッチのように機能します。したがって、入力電圧は負荷抵抗の両端に完全に現れて出力を生成します$V_{0}$。
Negative Cycle of the Input−入力の負のサイクルにより、回路内のポイントAがポイントBに対して負になります。これにより、ダイオードが逆バイアスされ、オープンスイッチのように機能します。したがって、負荷抵抗の両端の電圧はゼロになります。$V_{0}$ ゼロ。
波形
上の図で波形を観察すると、負のピークの一部しかクリップされていないことがわかります。これは、両端の電圧によるものです$V_{0}$。しかし、理想的な出力はそうなることを意図していませんでした。次の図を見てみましょう。
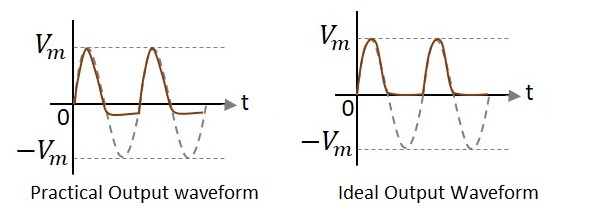
理想的な出力とは異なり、ダイオードの導通電圧が0.7vであるため、実際の出力には負のサイクルのビット部分が存在します。したがって、実際の出力波形と理想的な出力波形には違いがあります。
ポジティブシリーズクリッパー $V_{r}$
ダイオードが入力信号に直列に接続され、正の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の負の部分を減衰させるものは、次のように呼ばれます。 Negative Series Clipper with positive $V_{r}$。次の図は、印加された基準電圧が正の場合の負の直列クリッパーの回路図を表しています。
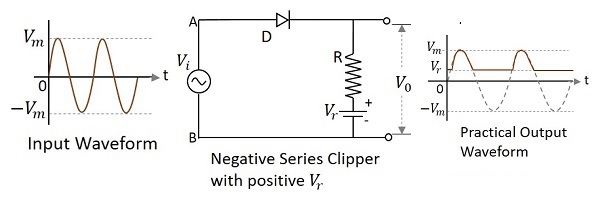
入力の正のサイクル中、ダイオードは、アノード電圧値がダイオードのカソード電圧値を超えた場合にのみ導通を開始します。カソード電圧は印加された基準電圧に等しいため、出力は次のようになります。
ネガティブシリーズクリッパーネガティブ付き $V_{r}$
ダイオードが入力信号に直列に接続され、負の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の負の部分を減衰させるものは、次のように呼ばれます。 Negative Series Clipper with negative $V_{r}$。次の図は、印加された基準電圧が負の場合の負の直列クリッパーの回路図を表しています。
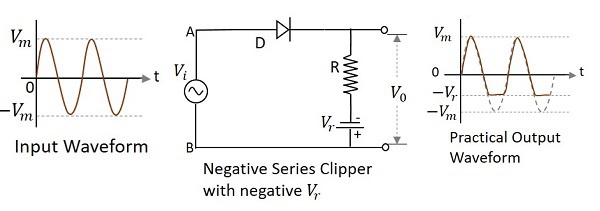
入力の正のサイクル中に、ダイオードは順方向にバイアスされ、入力信号が出力に現れます。負のサイクルの間、ダイオードは逆バイアスされるため、導通しません。ただし、印加されている負の基準電圧が出力に現れます。したがって、出力波形の負のサイクルは、この基準レベルの後でクリップされます。
ネガティブシャントクリッパー
ダイオードが入力信号にシャントで接続され、波形の負の部分を減衰させるクリッパー回路は、ネガティブシャントクリッパーと呼ばれます。次の図は、の回路図を表しています。negative shunt clipper。
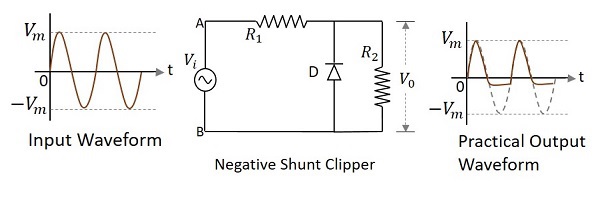
Positive Cycle of the Input−入力電圧が印加されると、入力の正のサイクルにより、回路内のポイントAがポイントBに対して正になります。これにより、ダイオードが逆バイアスされ、オープンスイッチのように動作します。したがって、負荷抵抗の両端の電圧は、出力に完全に現れるため、印加された入力電圧に等しくなります。$V_{0}$
Negative Cycle of the Input−入力の負のサイクルにより、回路内のポイントAがポイントBに対して負になります。これにより、ダイオードが順方向にバイアスされるため、閉じたスイッチのように動作します。したがって、負荷抵抗に電流が流れないため、負荷抵抗の両端の電圧はゼロになります。
波形
上の図では、波形を観察すると、負のピークの一部だけがクリップされていることがわかります。これは、両端の電圧によるものです$V_{0}$。しかし、理想的な出力はそうなることを意図していませんでした。次の図を見てみましょう。
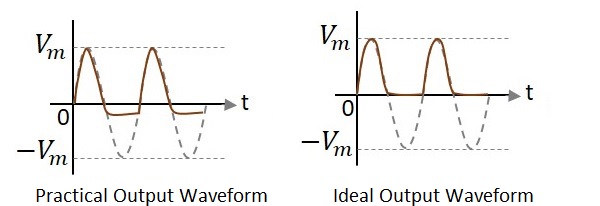
理想的な出力とは異なり、ダイオードの導通電圧が0.7vであるため、実際の出力には負のサイクルのビット部分が存在します。したがって、実際の出力波形と理想的な出力波形には違いがあります。
ポジティブのネガティブシャントクリッパー $V_{r}$
ダイオードが入力信号にシャント接続され、正の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の負の部分を減衰させるものは、次のように呼ばれます。 Negative Shunt Clipper with positive $V_{r}$。次の図は、印加された基準電圧が正の場合の負のシャントクリッパーの回路図を表しています。
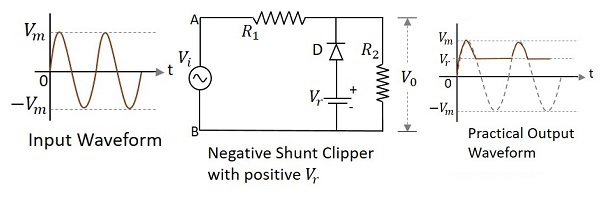
入力の正のサイクル中に、ダイオードは逆バイアスされ、オープンスイッチとして動作します。そのため、印加された基準電圧よりも大きい入力電圧全体が出力に現れます。基準電圧レベルを下回る信号はクリップオフされます。
負の半サイクルの間、ダイオードが順方向にバイアスされてループが完了すると、出力は存在しません。
ネガティブシャントクリッパー $V_{r}$
ダイオードが入力信号にシャント接続され、負の基準電圧でバイアスされているクリッパー回路 $V_{r}$ 波形の負の部分を減衰させるものは、次のように呼ばれます。 Negative Shunt Clipper with negative $V_{r}$。次の図は、印加された基準電圧が負の場合の負のシャントクリッパーの回路図を表しています。
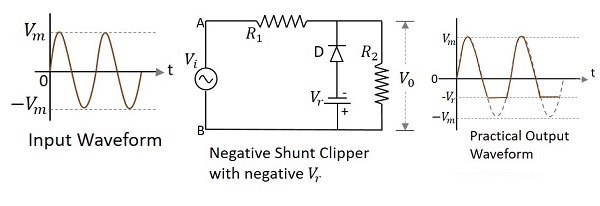
入力の正のサイクル中に、ダイオードは逆バイアスされ、オープンスイッチとして動作します。したがって、入力電圧全体が出力に現れます$V_{o}$。負の半サイクルの間、ダイオードは順方向にバイアスされます。基準電圧までの負電圧が出力に到達し、残りの信号がクリップオフされます。
双方向クリッパー
これは、基準電圧を備えた正および負のクリッパーです。 $V_{r}$。入力電圧は、2つの基準電圧で入力波形の正と負の両方の部分で双方向にクリップされます。このために、2つのダイオード$D_{1}$ そして $D_{2}$ 2つの基準電圧とともに $V_{r1}$ そして $V_{r2}$ 回路に接続されています。
この回路は、 Combinational Clipper回路。次の図は、双方向または組み合わせクリッパー回路の回路配置とその出力波形を示しています。
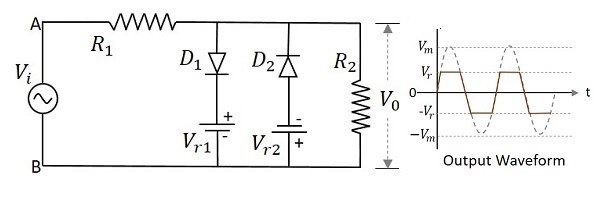
入力信号の正の半分の間、ダイオード $D_{1}$ 基準電圧を作ります $V_{r1}$出力に表示されます。入力信号の負の半分の間、ダイオード$D_{2}$ 基準電圧を作ります $V_{r1}$出力に表示されます。したがって、両方のダイオードが交互に導通して、両方のサイクル中に出力をクリップします。出力は負荷抵抗の両端で取得されます。
これで、主要なクリッパー回路が完成しました。次の章のクランパー回路に行きましょう。
クランパー回路は、AC信号にDCレベルを追加する回路です。実際には、信号の正と負のピークは、クランプ回路を使用して目的のレベルに配置できます。DCレベルがシフトすると、クランパー回路はLevel Shifter。
クランパー回路は、コンデンサーのようなエネルギー貯蔵要素で構成されています。単純なクランパー回路は、コンデンサー、ダイオード、抵抗器、および必要に応じてDCバッテリーで構成されます。
クランパー回路
クランパー回路は、印加された信号の実際の外観を変えることなく、波形を目的のDCレベルにシフトするダイオード、抵抗、およびコンデンサで構成される回路として定義できます。
波形の期間を維持するために、 tau 半分の時間より長くなければなりません(コンデンサの放電時間は遅くなければなりません)。
$$\tau = Rc$$
どこ
- Rは使用する抵抗の抵抗です
- Cは使用するコンデンサの静電容量です
コンデンサの充電と放電の時定数は、クランパー回路の出力を決定します。
クランパー回路では、入力信号に対して出力波形で上向きまたは下向きの垂直シフトが発生します。
負荷抵抗とコンデンサが波形に影響を与えます。したがって、コンデンサの放電時間は十分に長くする必要があります。
コンデンサ結合ネットワークが使用されている場合(コンデンサがDCをブロックするため)、入力に存在するDC成分は拒否されます。したがって、dc する必要があります restored、クランプ回路を使用しています。
クランパーの種類
クランパー回路には、次のようないくつかのタイプがあります。
- ポジティブクランパー
- ポジティブクランパー $V_r$
- ネガティブ付きポジティブクランパー $V_r$
- ネガティブクランパー
- ポジティブのネガティブクランパー $V_{r}$
- ネガティブ付きネガティブクランパー $V_{r}$
それらについて詳しく見ていきましょう。
ポジティブクランパー回路
クランプ回路はDCレベルを回復します。信号の負のピークがゼロレベルより上に上がると、信号は次のようになります。positively clamped。
正クランパー回路は、ダイオード、抵抗、コンデンサで構成され、出力信号を入力信号の正の部分にシフトする回路です。下の図は、ポジティブクランパー回路の構造を説明しています。
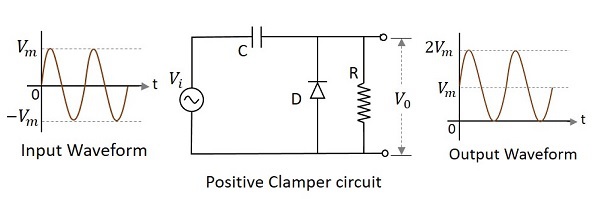
最初に入力が与えられたとき、コンデンサはまだ充電されておらず、ダイオードは逆バイアスされています。この時点では、出力は考慮されません。負の半サイクル中、ピーク値で、コンデンサは一方のプレートで負に、もう一方のプレートで正に充電されます。これで、コンデンサはピーク値まで充電されます。$V_{m}$。ダイオードは順方向にバイアスされており、導通が大きくなっています。
次の正の半サイクル中に、コンデンサは正のVmに充電され、ダイオードは逆バイアスされて開回路になります。このときの回路の出力は
$$V_{0}=V_{i}+V_{m}$$
したがって、上の図に示すように、信号は確実にクランプされます。出力信号は入力の変化に応じて変化しますが、入力電圧を加算するため、コンデンサの電荷に応じてレベルがシフトします。
正のVrを持つ正のクランパー
正の基準電圧でバイアスされている場合、正のクランパー回路は、その電圧が出力に追加されて、クランプされたレベルを上げます。これを使用して、正の基準電圧を持つ正のクランパーの回路は次のように構成されます。
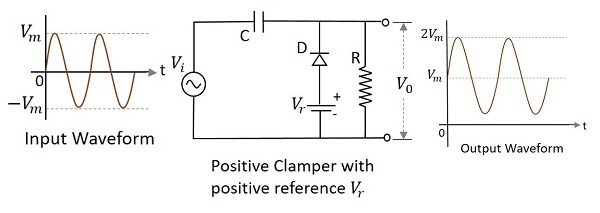
正の半サイクルの間、基準電圧は出力でダイオードを介して印加され、入力電圧が増加すると、ダイオードのカソード電圧がアノード電圧に対して増加するため、導通が停止します。負の半サイクルの間、ダイオードは順方向にバイアスされ、導通を開始します。コンデンサ両端の電圧と基準電圧が一緒になって出力電圧レベルを維持します。
ネガティブとポジティブクランパー $V_{r}$
正のクランパー回路が負の基準電圧でバイアスされている場合、その電圧が出力に追加されてクランプレベルが上がります。これを使用して、正の基準電圧を持つ正のクランパーの回路は次のように構成されます。
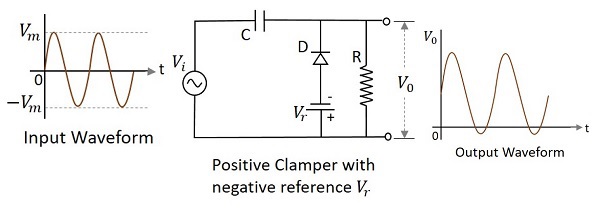
正の半サイクルの間、コンデンサ両端の電圧と基準電圧が一緒になって出力電圧レベルを維持します。負の半サイクルの間、カソード電圧がアノード電圧より低くなると、ダイオードが導通します。これらの変更により、上図に示すように出力電圧が変化します。
ネガティブクランパー
ネガティブクランパー回路は、ダイオード、抵抗、コンデンサで構成され、出力信号を入力信号の負の部分にシフトする回路です。下の図は、負のクランパー回路の構造を説明しています。
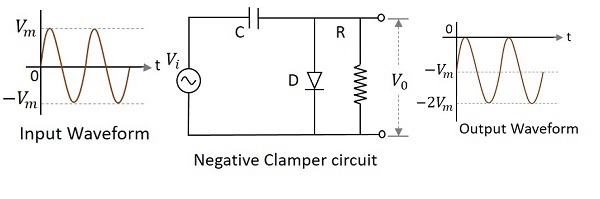
正の半サイクル中に、コンデンサはそのピーク値まで充電されます $v_{m}$。ダイオードは順方向にバイアスされ、導通します。負の半サイクルの間、ダイオードは逆バイアスされ、開回路になります。このときの回路の出力は
$$V_{0}=V_{i}+V_{m}$$
したがって、上の図に示すように、信号は負にクランプされます。出力信号は入力の変化に応じて変化しますが、入力電圧を加算するため、コンデンサの電荷に応じてレベルがシフトします。
正のVrを持つ負のクランパー
負のクランパー回路が正の基準電圧でバイアスされている場合、その電圧が出力に追加され、クランプレベルが上がります。これを使用して、正の基準電圧を持つ負のクランパーの回路は次のように構成されます。
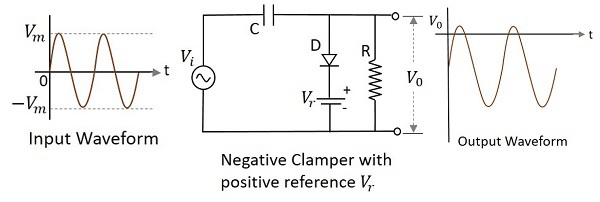
出力電圧は負にクランプされますが、印加される基準電圧が正であるため、出力波形の一部が正のレベルに上昇します。正の半サイクルの間、ダイオードは導通しますが、出力は印加された正の基準電圧に等しくなります。負の半サイクルの間、ダイオードは開回路として機能し、コンデンサの両端の電圧が出力を形成します。
負のVrを使用した負のクランパー
負の基準電圧でバイアスされている場合、負のクランパー回路は、その電圧が出力に追加され、クランプされたレベルを上げます。これを使用して、負の基準電圧を持つ負のクランパーの回路は次のように構成されます。
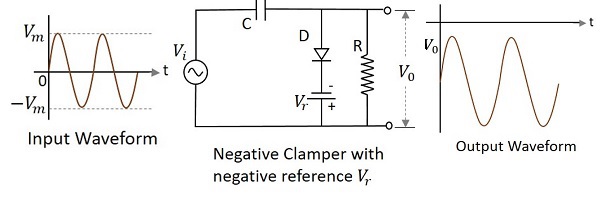
ダイオードのカソードは、ゼロおよびアノード電圧よりも低い負の基準電圧に接続されています。したがって、ダイオードは、ゼロ電圧レベルの前の正の半サイクル中に導通を開始します。負の半サイクルの間、コンデンサの両端の電圧が出力に現れます。したがって、波形は負の部分に向かってクランプされます。
アプリケーション
クリッパーとクランパーの両方に多くのアプリケーションがあります。
バリカン
- 波形の生成と整形に使用されます
- スパイクから回路を保護するために使用されます
- 振幅復元器に使用
- 電圧リミッターとして使用
- テレビ回路で使用
- FMトランスミッターで使用
クランパー
- 直流復元器として使用
- 歪みを取り除くために使用されます
- 電圧マルチプライヤとして使用
- アンプの保護に使用されます
- テスト機器として使用
- ベースラインスタビライザーとして使用
クリッパーやクランパーなどの波形整形回路に加えて、ダイオードを使用して、リミッターや電圧逓倍器などの他の回路を構築します。これについては、この章で説明します。ダイオードには、整流器と呼ばれる別の重要なアプリケーションもあります。これについては後で説明します。
リミッター
これらのクリッパーやクランパーを通過するときによく出くわすもう1つの名前は、リミッター回路です。Alimiter 回路は、出力電圧が所定の値を超えないように制限する回路として理解できます。
これは多かれ少なかれ、信号の指定された値を超えることを許可しないクリッパー回路です。実際には、クリッピングは極端な制限の範囲と言えます。したがって、制限はスムーズなクリッピングとして理解できます。
次の画像は、リミッター回路のいくつかの例を示しています-
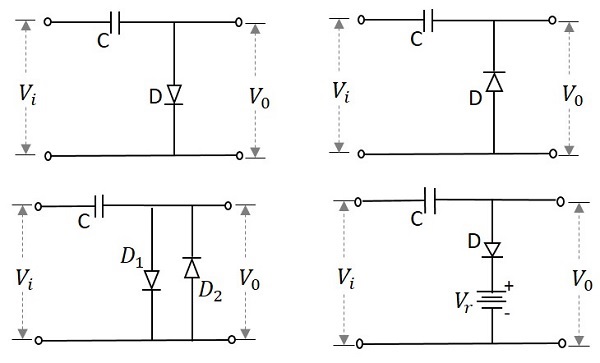
リミッター回路の性能は、その伝達特性曲線から理解できます。このような曲線の例は次のとおりです。
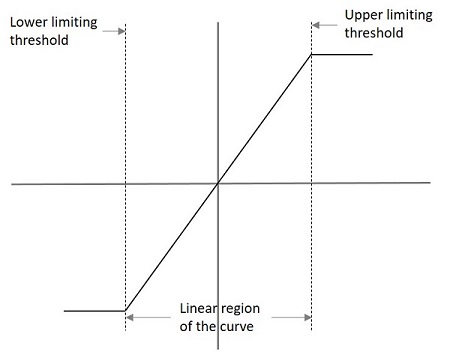
リミッターの特性を示す下限と上限がグラフに示されています。このようなグラフの出力電圧は、次のように理解できます。
$$V_{0}= L_{-},KV_{i},L_{+}$$
どこ
$$L_{-}=V_{i}\leq \frac{L_{-}}{k}$$
$$ KV_ {i} = \ frac {L _ {-}} {k} <V_ {i} <\ frac {L _ {+}} {k} $$
$$L_{+}=V_{i}\geq \frac{L_{+}}{K}$$
リミッターの種類
のようなリミッターのいくつかのタイプがあります
Unipolar Limiter −この回路は信号を一方向に制限します。
Bipolar Limiter −この回路は、2つの方法で信号を制限します。
Soft Limiter −この回路では、入力がわずかに変化しても、出力が変化する場合があります。
Hard Limiter −入力信号の変化に伴って出力が変化しにくい。
Single Limiter −この回路は制限用に1つのダイオードを採用しています。
Double Limiter −この回路は制限用に2つのダイオードを採用しています。
電圧逓倍器
場合によっては、電圧を乗算する必要があるアプリケーションがあります。これは、ダイオードとコンデンサを使用した単純な回路の助けを借りて簡単に行うことができます。電圧が2倍になると、そのような回路は電圧ダブラと呼ばれます。これを拡張して、VoltageTriplerやVoltageQuadruplerなどを作成し、高いDC電圧を得ることができます。
理解を深めるために、電圧を2倍にする回路を考えてみましょう。この回路は次のように呼ぶことができます。 Voltage Doubler。次の図は、電圧ダブラの回路を示しています。
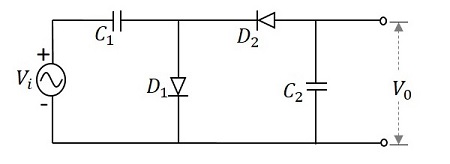
印加される入力電圧は、下図に示すように正弦波の形のAC信号になります。
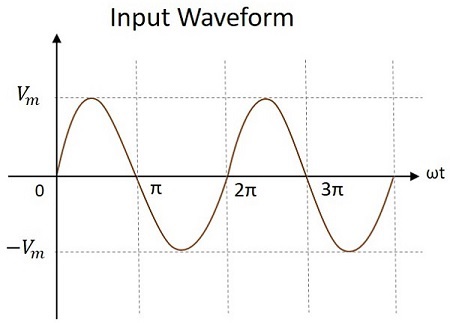
ワーキング
電圧逓倍回路は、入力信号の各半サイクルを分析することで理解できます。各サイクルにより、ダイオードとコンデンサは異なる方法で動作します。これを理解してみましょう。
During the first positive half cycle −入力信号が印加されると、コンデンサ $C_{1}$ 充電され、ダイオード $D_{1}$順方向にバイアスされています。ダイオードが$D_{2}$ 逆バイアスされ、コンデンサ $C_{2}$料金はかかりません。これにより、出力が作成されます$V_{0}$ することが $V_{m}$
これは次の図から理解できます。
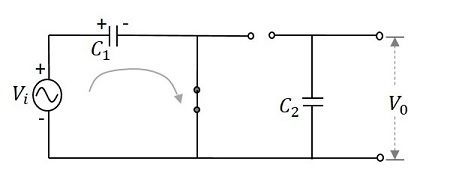
したがって、0から $\pi$、生成される出力電圧は $V_{max}$。コンデンサ$C_{1}$ 順方向にバイアスされたダイオードを介して充電されます $D_{1}$ 出力を与えるために、 $C_{2}$充電しません。この電圧は出力に現れます。
During the negative half cycle −その後、負の半サイクルが到来すると、ダイオード $D_{1}$ 逆バイアスがかかり、ダイオードが $D_{2}$順方向にバイアスされます。ダイオード$D_{2}$ コンデンサを介して電荷を取得します $C_{2}$このプロセス中に課金されます。その後、電流はコンデンサを流れます$C_{1}$放電します。次の図から理解できます。
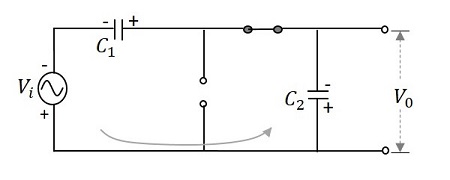
したがって、 $\pi$ に $2\pi$、コンデンサ両端の電圧 $C_{2}$ になります $V_{max}$。コンデンサが$C_{1}$完全に充電されていると、放電する傾向があります。これで、両方のコンデンサからの電圧が一緒に出力に現れます。$2V_{max}$。だから、出力電圧$V_{0}$ このサイクルの間は $2V_{max}$
During the next positive half cycle −コンデンサ $C_{1}$ 電源とダイオードから充電されます $D_{1}$順方向にバイアスされます。コンデンサ$C_{2}$ 放電する方法が見つからないため、電荷を保持し、ダイオード $D_{2}$逆バイアスになります。さて、出力電圧$V_{0}$ このサイクルの電圧は、出力に一緒に現れる両方のコンデンサから取得されます。 $2V_{max}$。
During the next negative half cycle −次の負の半サイクルでコンデンサが作成されます $C_{1}$ フル充電とダイオードから再び放電します $D_{1}$ バイアスを逆にする $D_{2}$ フォワードとコンデンサ $C_{2}$その電圧を維持するためにさらに充電します。さて、出力電圧$V_{0}$ このサイクルの電圧は、出力に一緒に現れる両方のコンデンサから取得されます。 $2V_{max}$。
したがって、出力電圧 $V_{0}$ 維持されている $2V_{max}$ 動作中、回路は電圧ダブラになります。
電圧逓倍器は主に、高いDC電圧が必要な場合に使用されます。たとえば、ブラウン管やコンピューターのディスプレイ。
分圧器
ダイオードを使用して電圧を乗算しますが、直列抵抗のセットを小さなネットワークにして電圧を分割することができます。このようなネットワークは、Voltage Divider ネットワーク。
分圧器は、大きな電圧を小さな電圧に変える回路です。これは、直列に接続された抵抗を使用して行われます。出力は入力の一部になります。出力電圧は、駆動する負荷の抵抗に依存します。
分圧回路がどのように機能するかを見てみましょう。次の図は、単純な分圧器ネットワークの例です。
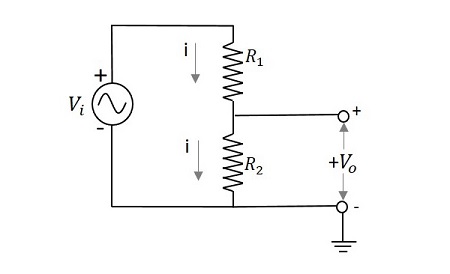
出力電圧の式を書こうとすると、
$$V_{i}=i\left ( R_{1}+R_{2} \right )$$
$$i=\frac{V-{i}}{\left ( R_{1}+R_{2} \right )}$$
$$V_{0}=i \:R_{2}\rightarrow \:i\:=\frac{V_{0}}{R_{2}}$$
両方を比較すると、
$$\frac{V_{0}}{R_{2}}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}$$
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
出力電圧の値を求める式です。したがって、出力電圧はネットワーク内の抵抗の抵抗値に応じて分割されます。異なる出力電圧の異なる割合を持つために、より多くの抵抗が追加されます。
分圧器についてもっと理解するために問題の例を挙げましょう。
例
2つの直列抵抗2kΩと5kΩを使用して、入力電圧が10vのネットワークの出力電圧を計算します。
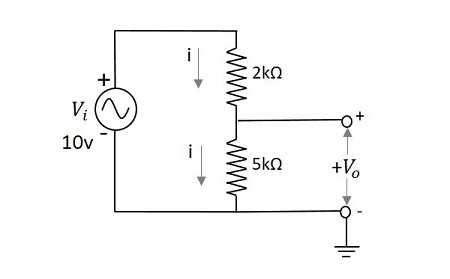
出力電圧 $V_{0}$ によって与えられます
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
$$=\frac{10}{\left ( 2 + 5 \right )k\Omega }5k\Omega$$
$$=\frac{10}{7}\times 5=\frac{50}{7}$$
$$=7.142v$$
出力電圧 $V_0$ 上記の問題の場合は7.14vです
ダイオードは、さまざまなアプリケーションで使用できる2端子PN接合です。そのようなアプリケーションの1つは電気スイッチです。PN接合は、順方向にバイアスされている場合は閉回路として機能し、逆方向にバイアスされている場合は開回路として機能します。したがって、順方向および逆方向にバイアスされた状態の変化により、ダイオードはスイッチとして機能します。forward であること ON そしてその reverse であること OFF 状態。

機械式スイッチ上の電気スイッチ
以下の理由により、電気スイッチは機械式スイッチよりも好ましい選択です。
- 機械式スイッチは金属が酸化されやすいのに対し、電気式スイッチは酸化されません。
- メカニカルスイッチには可動接点があります。
- 電気スイッチよりも応力やひずみが発生しやすい傾向があります。
- 機械式スイッチの摩耗や破れは、しばしばそれらの動作に影響を与えます。
したがって、電気スイッチは機械スイッチよりも便利です。
スイッチとしてのダイオードの動作
指定された電圧を超えると、ダイオードの抵抗が増加し、ダイオードが逆バイアスされ、オープンスイッチとして機能します。印加される電圧が基準電圧を下回ると、ダイオードの抵抗が減少し、ダイオードが順方向にバイアスされ、閉じたスイッチとして機能します。
次の回路は、スイッチとして機能するダイオードについて説明しています。
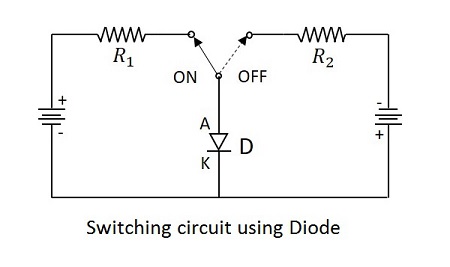
スイッチングダイオードには、P領域が低濃度にドープされ、N領域が高濃度にドープされたPN接合があります。上記の回路は、正の電圧がダイオードを順方向にバイアスするとダイオードがオンになり、負の電圧がダイオードを逆方向にバイアスするとオフになることを示しています。
リンギング
それまで順方向電流が流れると、突然の逆方向電圧で、すぐにオフになるのではなく、インスタンスに対して逆方向電流が流れます。漏れ電流が大きいほど、損失は大きくなります。ダイオードが突然逆バイアスされたときの逆電流の流れは、次のように呼ばれるいくつかの発振を生成することがありますRINGING。
このリンギング状態は損失であるため、最小限に抑える必要があります。これを行うには、ダイオードのスイッチング時間を理解する必要があります。
ダイオードスイッチング時間
バイアス条件を変更している間、ダイオードは transient response。平衡位置からの突然の変化に対するシステムの応答は、過渡応答と呼ばれます。
順方向から逆方向へ、および逆方向から順方向バイアスへの突然の変化は、回路に影響を与えます。このような突然の変化に対応するのにかかる時間は、電気スイッチの有効性を定義するための重要な基準です。
ダイオードが定常状態に戻るまでにかかる時間は、次のように呼ばれます。 Recovery Time。
ダイオードが逆バイアス状態から順バイアス状態に切り替わるまでにかかる時間間隔は、次のように呼ばれます。 Forward Recovery Time.($t_{fr}$)
ダイオードが順方向バイアス状態から逆方向バイアス状態に切り替わるまでにかかる時間間隔は、次のように呼ばれます。 Reverse Recovery Time. ($t_{fr}$)
これをより明確に理解するために、スイッチングPNダイオードに電圧を印加するとどうなるかを分析してみましょう。
キャリア濃度
少数電荷キャリア濃度は、接合部から離れて見られるように指数関数的に減少します。電圧が印加されると、順方向にバイアスされた状態のため、一方の大部分のキャリアがもう一方の側に移動します。彼らは反対側の少数キャリアになります。この濃度は接合部でより高くなります。
たとえば、Nタイプを考慮すると、順方向バイアスを適用した後にNタイプに入る過剰な正孔は、Nタイプ材料の既存の少数キャリアに追加されます。
いくつかの表記法を考えてみましょう。
- P型(穴)の多数キャリア= $P_{po}$
- N型(電子)の多数キャリア= $N_{no}$
- P型(電子)の少数キャリア= $N_{po}$
- N型(穴)の多数キャリア= $P_{no}$
During Forward biased Condition−少数キャリアは、接合部に近く、接合部から離れていません。下のグラフはこれを説明しています。
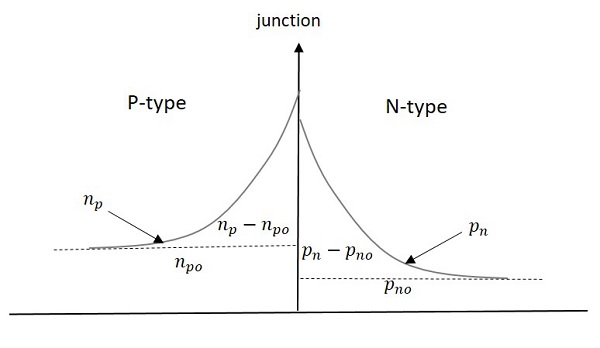
Pタイプの過剰な少数キャリア電荷= $P_n-P_{no}$ と $p_{no}$ (定常状態値)
N型の過剰な少数キャリア電荷= $N_p-N_{po}$ と $N_{po}$ (定常状態値)
During reverse bias condition−多数キャリアは接合部に電流を流さないため、現在の状態には関与しません。スイッチングダイオードは、インスタンスに対して逆方向の短絡として動作します。
少数キャリアは接合部を通過し、電流を伝導します。 Reverse Saturation Current。次のグラフは、逆バイアス中の状態を表しています。

上図において、点線は平衡値を表し、実線は実際の値を表します。少数の電荷キャリアによる電流は伝導するのに十分な大きさであるため、この過剰な電荷が除去されるまで回路はオンになります。
ダイオードが順バイアスから逆バイアスに変化するのに必要な時間は、 Reverse recovery time ($t_{rr}$)。次のグラフは、ダイオードのスイッチング時間を詳細に説明しています。
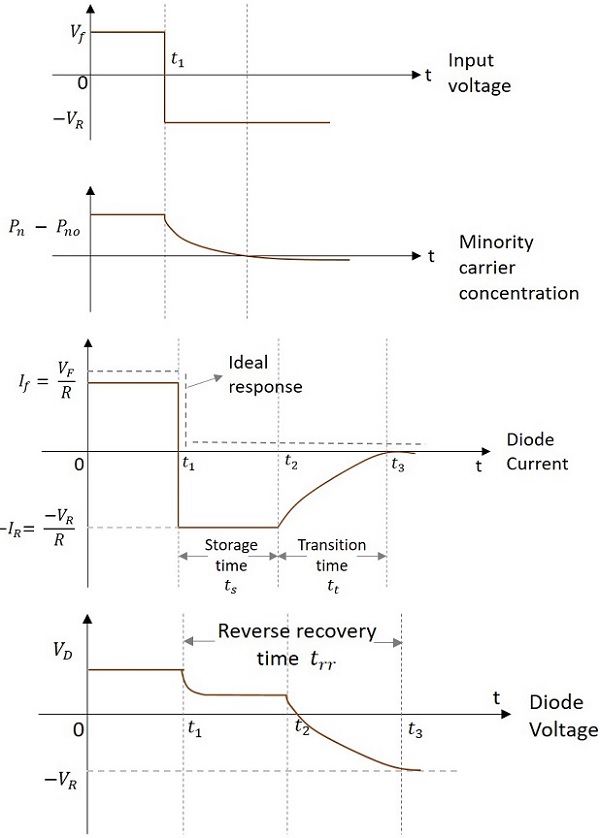
上図から、ダイオード電流グラフを考えてみましょう。
で $t_{1}$ダイオードがON状態から突然OFF状態になります。それは保存時間として知られています。Storage timeは、過剰な少数キャリア電荷を取り除くために必要な時間です。N型からP型の材料に流れる負の電流は、保管期間中にかなりの量になります。この負の電流は、
$$-I_R= \frac{-V_{R}}{R}$$
次の期間は transition time」(から $t_2$ に $t_3$)
遷移時間は、ダイオードが完全に開回路状態になるまでにかかる時間です。後$t_3$ダイオードは定常状態の逆バイアス状態になります。前$t_1$ ダイオードは定常状態の順方向バイアス状態にあります。
したがって、完全に開回路状態になるまでにかかる時間は次のとおりです。
$$Reverse \:\:recovery\:\: time\left ( t_{rr} \right )= Storage \:\:time \left ( T_{s} \right )+Transition \:\: time \left ( T_{t} \right )$$
OFFからON状態になるのに対し、 Forward recovery time。逆回復時間は順回復時間よりも長くなります。この逆回復時間が短くなると、ダイオードはより良いスイッチとして機能します。
定義
議論された期間の定義を見てみましょう。
Storage time −逆バイアス状態でもダイオードが導通状態にある時間は、次のように呼ばれます。 Storage time。
Transition time −非導通状態、つまり定常状態の逆バイアスに戻るまでに経過した時間は、 Transition time。
Reverse recovery time −ダイオードが順バイアスから逆バイアスに変化するのに必要な時間は次のように呼ばれます。 Reverse recovery time。
Forward recovery time −ダイオードが逆バイアスから順バイアスに変化するのに必要な時間は次のように呼ばれます。 Forward recovery time。
ダイオードのスイッチング時間に影響を与える要因
ダイオードのスイッチング時間に影響を与える要因はいくつかあります。
Diode Capacitance − PN接合容量は、バイアス条件によって変化します。
Diode Resistance −ダイオードの状態を変化させるためにダイオードが提供する抵抗。
Doping Concentration −ダイオードのドーピングレベルは、ダイオードのスイッチング時間に影響します。
Depletion Width−空乏層の幅が狭いほど、スイッチングが速くなります。ツェナーダイオードはアバランシェダイオードよりも空乏領域が狭いため、アバランシェダイオードの方が優れたスイッチになります。
アプリケーション
ダイオードスイッチング回路が使用される多くのアプリケーションがあります。
- 高速整流回路
- 高速スイッチング回路
- RF受信機
- 汎用アプリケーション
- コンシューマーアプリケーション
- 自動車用途
- テレコムアプリケーションなど。
この章では、ダイオード回路の別のセクションに関する新たなスタートを提供します。日常生活で出会う電源回路をご紹介します。すべての電子機器は、その電子機器のさまざまなセクションに必要な量のACまたはDC電源を供給する電源ユニットで構成されています。
電源の必要性
コンピュータ、テレビ、ブラウン管オシロスコープなどの電子機器には多くの小さなセクションがありますが、これらのセクションはすべて、230VAC電源を必要としません。
代わりに、1つ以上のセクションで12v DCが必要な場合がありますが、他のセクションでは30vDCが必要な場合があります。必要なDC電圧を供給するために、入力230vAC電源を使用のために純粋なDCに変換する必要があります。ザ・Power supply units 同じ目的を果たします。
実用的な電源ユニットは次の図のようになります。

ここで、電源ユニットを構成するさまざまな部品について説明します。
電源の部品
代表的な電源ユニットは以下のもので構成されています。
Transformer − 230vAC電源を降圧するための入力トランス。
Rectifier −信号に存在するAC成分をDC成分に変換する整流回路。
Smoothing −整流された出力に存在する変動を平滑化するためのフィルタリング回路。
Regulator −電圧を目的の出力レベルに制御するための電圧レギュレータ回路。
Load −安定化出力からの純粋なDC出力を使用する負荷。
電源ユニットのブロック図
安定化電源ユニットのブロック図は以下のとおりです。
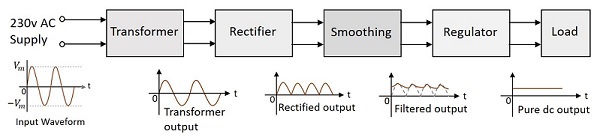
上の図から、トランスが初期段階に存在していることがわかります。BASIC ELECTRONICSチュートリアルでは、トランスに関する概念についてはすでに説明しましたが、それを一瞥してみましょう。
変成器
変圧器には primary coil これに input 与えられ、 secondary coil そこから output収集されます。これらのコイルは両方ともコア材料に巻かれています。通常、絶縁体はCore 変圧器の。
次の図は、実際のトランスを示しています。
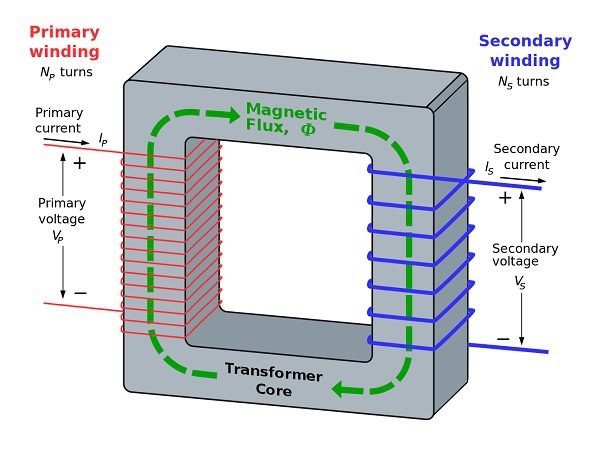
上の図から、いくつかの表記法が一般的であることが明らかです。それらは次のとおりです-
$N_{p}$ =一次巻線の巻数
$N_{s}$ = 2次巻線の巻数
$I_{p}$ =変圧器の一次側に流れる電流
$I_{s}$ =トランスの2次側に流れる電流
$V_{p}$ =変圧器の一次側の電圧
$V_{s}$ =トランスの2次側の電圧
$\phi$ =トランスのコアの周りに存在する磁束
回路内の変圧器
次の図は、回路内でトランスがどのように表されるかを示しています。トランスの一次巻線、二次巻線、およびコアも次の図に示されています。
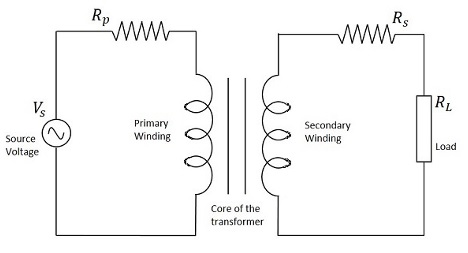
したがって、変圧器が回路に接続されると、入力電源が一次コイルに与えられ、この電源でさまざまな磁束が生成され、その磁束が変圧器の二次コイルに誘導され、次のさまざまなEMFが生成されます。変化する磁束。磁束は変化するはずなので、EMFを一次から二次に転送する場合、変圧器は常に交流ACで動作します。
二次巻線の巻数に応じて、トランスは次のいずれかに分類できます。 Step-up または Step-down 変成器。
ステップアップトランス
二次巻線が一次巻線よりも巻数が多い場合、変圧器は Step-up変成器。ここで、誘導起電力は入力信号よりも大きくなります。
下の図は、昇圧トランスの記号を示しています。
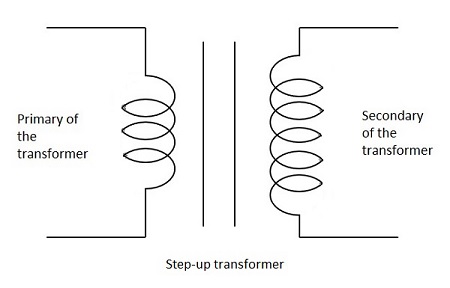
ステップダウントランス
二次巻線の巻数が一次巻線よりも少ない場合、変圧器は Step-down変成器。ここで、誘導起電力は入力信号よりも小さくなります。
下の図は、降圧トランスの記号を示しています。
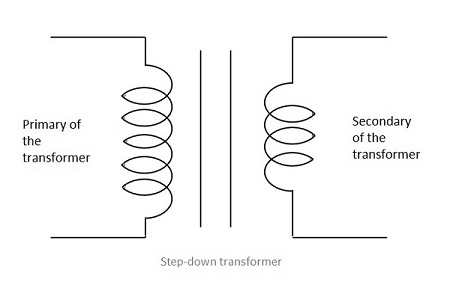
私たちの電源回路では、 Step-down transformer、DCへのAC電力を減らす必要があるため。この降圧トランスの出力は電力が少なくなり、これは次のセクションへの入力として与えられます。rectifier。整流器については次の章で説明します。
AC電源をDC電源に変換する必要が生じたときはいつでも、整流回路が助けになります。単純なPN接合ダイオードが整流器として機能します。ダイオードの順方向バイアスと逆方向バイアスの条件により、整流が行われます。
整流
交流には、その状態を連続的に変化させる性質があります。これは、交流が示される正弦波を観察することで理解できます。正の方向に上昇し、正のピーク値になり、そこから通常に減少し、再び負の部分になり、負のピークに達し、再び通常に戻って続行します。
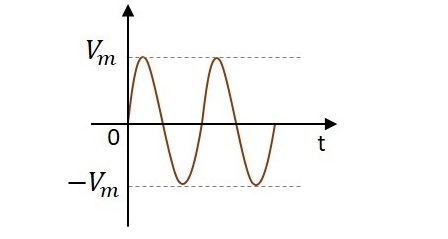
波の形成の旅の間に、私たちは波が正と負の方向に進むのを観察することができます。実際には完全に変化するため、名前は交流です。
しかし、整流の過程で、この交流は直流DCに変化します。それまで正と負の両方向に流れる波は、DCに変換すると正の方向にのみ方向が制限されます。したがって、下の図のように、電流は正の方向にのみ流れることができ、負の方向に抵抗されます。

整流を行う回路は、 Rectifier circuit。ダイオードは、整流回路を構築するための整流器として使用されます。
整流回路の種類
整流回路には、出力に応じて2つの主要なタイプがあります。彼らです
- 半波整流器
- 全波整流器
半波整流回路は入力電源の正の半サイクルのみを整流しますが、全波整流回路は入力電源の正と負の両方の半サイクルを整流します。
半波整流器
半波整流器という名前自体は、 rectification のためだけに行われます halfサイクルの。AC信号は、使用法に応じてステップアップまたはステップダウンする入力トランスを介して供給されます。ほとんどの場合、入力電圧を下げるために、整流回路には降圧トランスが使用されます。
トランスに与えられた入力信号は、整流器として機能するPN接合ダイオードを通過します。このダイオードは、入力の正の半サイクルの間だけ、AC電圧を脈動DCに変換します。回路の最後に負荷抵抗が接続されています。下の図は、半波整流器の回路を示しています。
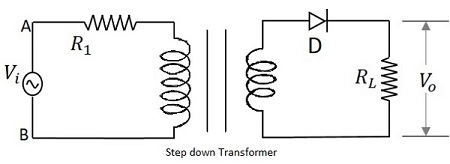
HWRの動作
T入力信号は変圧器に与えられ、電圧レベルを下げます。トランスからの出力は、整流器として機能するダイオードに与えられます。このダイオードは、入力信号の正の半サイクルでオン(導通)します。したがって、回路に電流が流れ、負荷抵抗の両端で電圧降下が発生します。ダイオードは負の半サイクルでオフになる(導通しない)ため、負の半サイクルの出力は次のようになります。$i_{D} = 0$ そして $V_{o}=0$。
したがって、出力は入力電圧の正の半サイクルの間のみ存在します(逆リーク電流は無視します)。この出力は脈動し、負荷抵抗の両端で発生します。
HWRの波形
入力波形と出力波形は次の図のようになります。
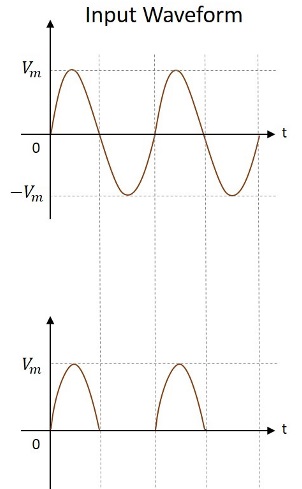
したがって、半波整流器の出力は脈流DCです。半波整流器の出力から得られるいくつかの値を理解することにより、上記の回路を分析してみましょう。
半波整流器の分析
半波整流回路を解析するために、入力電圧の式を考えてみましょう。
$$v_{i}=V_{m} \sin \omega t$$
$V_{m}$ は供給電圧の最大値です。
ダイオードが理想的であると仮定しましょう。
- 順方向、つまりオン状態の抵抗は $R_f$。
- 逆方向、つまりオフ状態の抵抗は $R_r$。
現在 i ダイオードまたは負荷抵抗で $R_L$ によって与えられます
$i=I_m \sin \omega t \quad for\quad 0\leq \omega t\leq 2 \pi$
$ i=0 \quad\quad\quad\quad for \quad \pi\leq \omega t\leq 2 \pi$
どこ
$$I_m= \frac{V_m}{R_f+R_L}$$
DC出力電流
平均電流 $I_{dc}$ によって与えられます
$$I_{dc}=\frac{1}{2 \pi}\int_{0}^{2 \pi} i \:d\left ( \omega t \right )$$
$$=\frac{1}{2 \pi}\left [ \int_{0}^{\pi}I_m \sin \omega t \:d\left ( \omega t \right )+\int_{0}^{2 \pi}0\: d\left ( \omega t \right )\right ]$$
$$=\frac{1}{2 \pi}\left [ I_m\left \{-\cos \omega t \right \}_{0}^{\pi} \right ]$$
$$=\frac{1}{2 \pi}\left [ I_m\left \{ +1-\left ( -1 \right ) \right \} \right ]=\frac{I_m}{\pi}=0.318 I_m$$
の値を代入する $I_m$、 我々が得る
$$I_{dc}=\frac{V_m}{\pi\left ( R_f+R_L \right )}$$
場合 $R_L >> R_f$、その後
$$I_{dc}=\frac{V_m}{\pi R_L}=0.318 \frac{V_m}{R_L}$$
DC出力電圧
DC出力電圧は次の式で与えられます。
$$ V_{dc}=I_{dc}\times R_L=\frac{I_m}{\pi}\times R_L$$
$$=\frac{V_m\times R_L}{\pi\left (R_f+R_L \right )}=\frac{V_m}{\pi\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
場合 $R_L>>R_f$、その後
$$V_{dc}=\frac{V_m}{\pi}=0.318 V_m$$
RMS電流と電圧
RMS電流の値は次の式で与えられます。
$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{2\pi} i^{2} d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{2\pi}I_{m}^{2} \sin^{2}\omega t \:d\left (\omega t \right ) +\frac{1}{2\pi}\int_{\pi}^{2\pi} 0 \:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{2 \pi}\int_{0}^{\pi}\left ( \frac{1-\cos 2 \omega t}{2} \right )d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \left ( \omega t \right )-\frac{\sin 2 \omega t}{2} \right \}_{0}^{\pi}\right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \pi - 0 - \frac{\sin 2 \pi}{2}+ \sin 0 \right \} \right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{4 \pi} \right ]^{\frac{1}{2}}=\frac{I_m}{2}$$
$$=\frac{V_m}{2\left ( R_f+R_L \right )}$$
負荷両端のRMS電圧は
$$V_{rms}=I_{rms} \times R_L= \frac{V_m \times R_L}{2\left ( R_f+R_L \right )}$$
$$=\frac{V_m}{2\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
場合 $R_L>>R_f$、その後
$$V_{rms}=\frac{V_m}{2}$$
整流器の効率
どの回路も、より良い出力を得るために効率的に動作する必要があります。半波整流器の効率を計算するには、入力電力に対する出力電力の比率を考慮する必要があります。
整流器の効率は次のように定義されます。
$$\eta =\frac{d.c.power\:\: delivered \:\: to \:\: the \:\: load}{a.c.input \:\: power\:\:from\:\:transformer\:\:secondary}=\frac{P_{ac}}{P_{dc}}$$
今
$$P_{dc}=\left ( {I_{dc}} \right )^2 \times R_L=\frac{I_m R_L}{\pi^2}$$
さらに
$$P_{ac}=P_a+P_r$$
どこ
$P_a = power \:dissipated \:at \:the \:junction \:of \:diode$
$$=I_{rms}^{2}\times R_f=\frac{I_{m}^{2}}{4}\times R_f$$
そして
$$P_r = power \:dissipated \:in \:the \:load \:resistance$$
$$=I_{rms}^{2}\times R_L=\frac{I_{m}^{2}}{4}\times R_L$$
$$P_{ac}=\frac{I_{m}^{2}}{4}\times R_f+\frac{I_{m}^{2}}{4}\times R_L =\frac{I_{m}^{2}}{4}\left ( R_f+R_L \right )$$
の両方の表現から $P_{ac}$ そして $P_{dc}$、 私たちは書くことができます
$$\eta =\frac{I_{m}^{2}R_L/\pi^2}{I_{m}^{2}\left ( R_f+R_L \right )/4}=\frac{4}{\pi^2}\frac{R_L}{\left ( R_f+R_L \right )}$$
$$=\frac{4}{\pi^2}\frac{1}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}=\frac{0.406}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
整流器の効率のパーセンテージ
$$\eta =\frac{40.6}{\lbrace1+\lgroup\: R_{f}/R_{L}\rgroup\rbrace}$$
理論的には、半波整流器の整流器効率の最大値は、次の場合に40.6%です。 $R_{f}/R_{L} = 0$
さらに、効率は以下の方法で計算することができる。
$$\eta =\frac{P_{dc}}{P_{ac}}=\frac{\left (I_{dc} \right )^2R_L}{\left ( I_{rms} \right )^2R_L}=\frac{\left ( V_{dc}/R_L \right )^2R_L}{\left (V_{rms}/R_L \right )^2R_L} =\frac{\left ( V_{dc} \right )^2}{\left ( V_{rms} \right )^2}$$
$$=\frac{\left ( V_m/ \pi \right )^2}{\left ( V_m/2 \right )^2}=\frac{4}{\pi^2}=0.406$$
$$=40.6\%$$
リップルファクター
整流された出力には、リップルの形で、その中に存在するAC成分がいくらか含まれています。これは、半波整流器の出力波形を観察することで理解できます。純粋なDCを取得するには、このコンポーネントについてのアイデアが必要です。
リップル係数は、整流された出力のうねりを示します。それはによって示されますy。これは、電圧または電流のAC成分の実効値と直接値または平均値の比率として定義できます。
$$\gamma =\frac{ripple \: voltage}{d.c \:voltage} =\frac{rms\:value\:of\: a.c.component}{d.c.value\:of\:wave}=\frac{\left ( V_r \right )_{rms}}{v_{dc}}$$
ここに、
$$\left ( V_r \right )_{rms}=\sqrt{V_{rms}^{2}-V_{dc}^{2}}$$
したがって、
$$\gamma =\frac{\sqrt{V_{rms}^{2}-V_{dc}^{2}}}{V_{dc}}=\sqrt{\left (\frac{V_{rms}}{V_{dc}} \right )^2-1}$$
さて、
$$V_{rms}=\left [ \frac{1}{2\pi}\int_{0}^{2\pi} V_{m}^{2} \sin^2\omega t\:d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$
$$=V_m\left [ \frac{1}{4\pi} \int_{0}^{\pi}\left ( 1- \cos2 \:\omega t \right )d\left ( \omega t \right )\right ]^{\frac{1}{2}}=\frac{V_m}{2}$$
$$V_{dc}=V_{av}=\frac{1}{2\pi}\left [ \int_{0}^{\pi}V_m \sin \omega t \:d\left ( \omega t \right )+\int_{0}^{2\pi} 0.d\left ( \omega t \right )\right ]$$
$$=\frac{V_m}{2 \pi}\left [ -\cos \omega t \right ]_{0}^{\pi}=\frac{V_m}{\pi}$$
$$\gamma =\sqrt{\left [ \left \{ \frac{\left ( V_m/2 \right )}{\left ( V_m/\pi \right )} \right \}^2-1 \right ]}=\sqrt{\left \{ \left ( \frac{\pi}{2} \right )^2-1 \right \}}=1.21$$
リップル係数は次のようにも定義されます。
$$\gamma =\frac{\left ( I_r \right )_{rms}}{I_{dc}}$$
半波整流器に存在するリップル係数の値は1.21であるため、出力に存在するACの量は次のようになります。 $121\%$ DC電圧の
規制
負荷を流れる電流は、負荷抵抗によって異なる場合があります。しかし、そのような状態でも、その負荷抵抗の両端にかかる出力電圧は一定であると予想されます。したがって、さまざまな負荷条件でも電圧を調整する必要があります。
DC負荷電流の変化に伴うDC出力電圧の変化は、次のように定義されます。 Regulation。規制率は次のように計算されます。
$$Percentage\:regulation=\frac{V_{no \:load}-V_{full\:load}}{V_{full\:load}} \times 100\%$$
規制の割合が低いほど、電源は良好になります。理想的な電源のレギュレーションはゼロパーセントです。
変圧器利用率
整流回路で負荷に供給されるDC電力は、回路で使用される変圧器の定格を決定します。
したがって、変圧器の使用率は次のように定義されます。
$$TUF=\frac{d.c.power\:to\:be\:delivered\:to\:the\:load}{a.c.rating\:of\:the\:transformer\:secondary}$$
$$=\frac{P_{d.c}}{P_{a.c\left ( rated \right )}}$$
変圧器の理論によれば、二次側の定格電圧は
$$V_m/\sqrt{2}$$
それを流れる実際のRMS電圧は
$$I_m/2$$
したがって、
$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left ( V_m/\sqrt{2} \right )\times\left ( I_m/2 \right )}$$
だが
$$V_m=I_m\left ( R_f+R_L \right )$$
したがって、
$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left \{ I_m\left ( R_f+R_L \right )/\sqrt{2} \right \}\times \left ( I_m/2 \right )}$$
$$=\frac{2\sqrt{2}}{\pi^2}\times \frac{R_L}{\left ( R_f+R_L \right )}$$
$$=\frac{2\sqrt{2}}{\pi^2} = 0.287$$
ピーク逆電圧
逆バイアスで接続されている場合、ダイオードは制御されたレベルの電圧で動作する必要があります。その安全電圧を超えると、ダイオードが損傷します。したがって、その最大電圧について知ることは非常に重要です。
ダイオードが破壊されることなく耐えることができる最大逆電圧は、 Peak Inverse Voltage。要するに、PIV。
ここで、PIVはVmに他なりません。
フォームファクタ
これは、波形上のすべてのポイントの絶対値の数学的平均として理解できます。ザ・form factor平均値に対するRMS値の比率として定義されます。それはによって示されますF。
$$F=\frac{rms\:value}{average\:value}=\frac{I_m/2}{I_m/\pi}=\frac{0.5I_m}{0.318I_m}=1.57$$
ピークファクター
リップルのピーク値は、整流がどれほど効果的かを知るために考慮する必要があります。ピークファクターの値も重要な考慮事項です。Peak factor RMS値に対するピーク値の比率として定義されます。
したがって、
$$Peak Factor=\frac{Peak\:value}{r.m.s\:value}=\frac{V_m}{V_m/2}=2$$
これらはすべて、整流器について研究する際に考慮すべき重要なパラメータです。
正と負の両方の半サイクルを整流する整流回路は、完全なサイクルを整流するため、全波整流器と呼ぶことができます。全波整流器の構造は2つのタイプで作ることができます。彼らです
- センタータップ全波整流器
- ブリッジ全波整流器
どちらにも長所と短所があります。ここで、それらの構築と波形の操作の両方を実行して、どちらが優れているのか、そしてその理由を理解しましょう。
センタータップ付き全波整流器
トランスの2次側をタップして目的の出力電圧を取得し、2つのダイオードを交互に使用してサイクル全体を整流する整流回路は、 Center-tapped Full wave rectifier circuit。他の場合とは異なり、トランスはここでセンタータップされています。
センタータップトランスの特徴は−
タッピングは、2次巻線の中間点にリード線を引くことによって行われます。この巻線は、そうすることによって2つの等しい半分に分割されます。
タップされた中間点の電圧はゼロです。これは中立点を形成します。
センタータップは、大きさが等しいが極性が互いに反対の2つの別々の出力電圧を提供します。
さまざまなレベルの電圧を得るために、いくつかのテーピングを引き出すことができます。
2つの整流ダイオードを備えたセンタータップ付きトランスは、 Center-tapped full wave rectifier。センタータップ全波整流器の回路図は以下のとおりです。
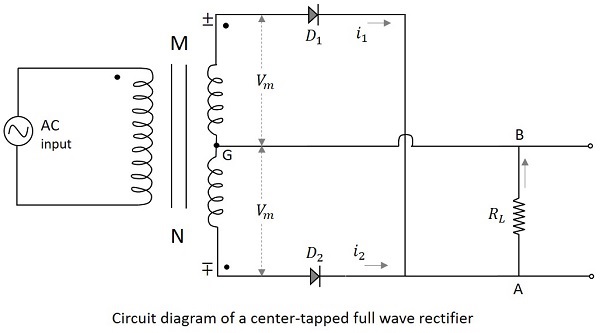
CT-FWRの動作
センタータップ付き全波整流器の動作は、上の図から理解できます。入力電圧の正の半サイクルが印加されると、トランスの2次側の点Mが点Nに対して正になります。これにより、ダイオードが作成されます。$D_1$順方向バイアス。したがって、現在$i_1$ 負荷抵抗を介してAからBに流れます。これで、出力に正の半サイクルがあります。
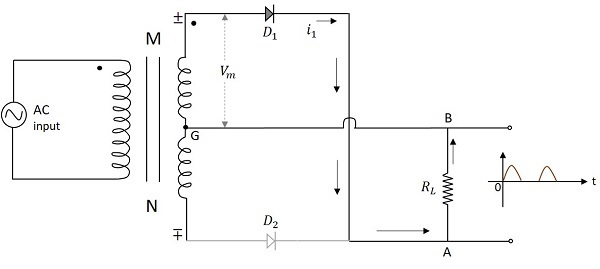
入力電圧の負の半サイクルが印加されると、トランスの2次側の点Mは点Nに対して負になります。これにより、ダイオードが作成されます。 $D_2$順方向バイアス。したがって、現在$i_2$ 負荷抵抗を介してAからBに流れます。これで、入力の負の半サイクル中でも、出力に正の半サイクルがあります。

CTFWRの波形
センタータップ全波整流器の入力波形と出力波形は次のとおりです。
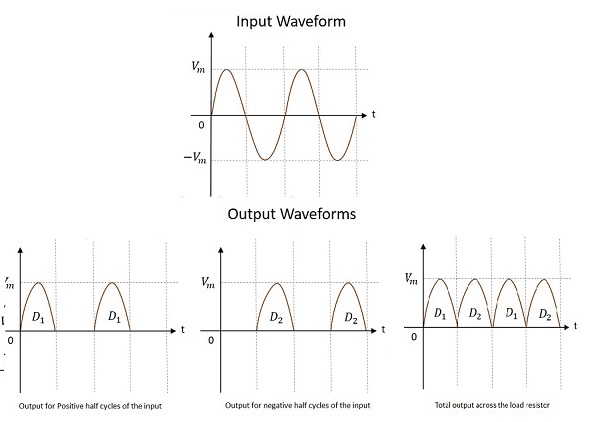
上の図から、正と負の両方の半サイクルで出力が得られていることがわかります。負荷抵抗の両端の出力がsame direction 両方の半サイクルで。
ピーク逆電圧
二次巻線の半分の両端の最大電圧は $V_m$、二次電圧全体が非導電性ダイオードの両端に現れます。従ってpeak inverse voltage は、半二次巻線の最大電圧の2倍です。
$$PIV=2V_m$$
短所
−などのセンタータップ全波整流器にはいくつかの欠点があります。
- センタータップの位置が難しい
- DC出力電圧が小さい
- ダイオードのPIVは高くなければなりません
次の種類の全波整流回路は Bridge Full wave rectifier circuit。
ブリッジ全波整流器
これは、ブリッジ形式で接続された4つのダイオードを使用して、入力の全サイクル中に出力を生成するだけでなく、センタータップ付き全波整流回路の欠点を排除するような全波整流回路です。
この回路では、トランスをセンタータップする必要はありません。と呼ばれる4つのダイオード$D_1$、 $D_2$、 $D_3$ そして $D_4$は、2つのダイオードが入力電源の半分のサイクルで導通し、2つのダイオードが残りの半サイクルで導通するようにブリッジタイプのネットワークを構築する際に使用されます。ブリッジ全波整流器の回路は次の図のようになります。
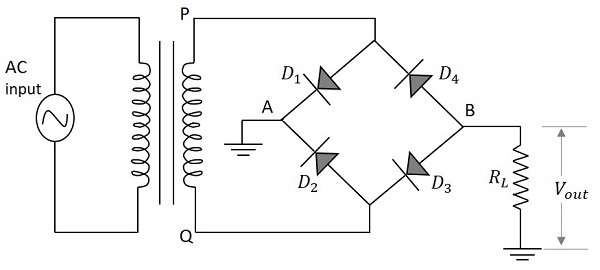
ブリッジ全波整流器の動作
ブリッジ回路に接続された4つのダイオードを備えた全波整流器は、より良い全波出力応答を得るために採用されています。入力電源の正の半サイクルが与えられると、ポイントPはポイントに対して正になりますQ。これはダイオードを作ります$D_1$ そして $D_3$ 前方バイアス $D_2$ そして $D_4$逆バイアス。これらの2つのダイオードは、負荷抵抗と直列になります。
次の図は、これを回路内の従来の電流フローとともに示しています。
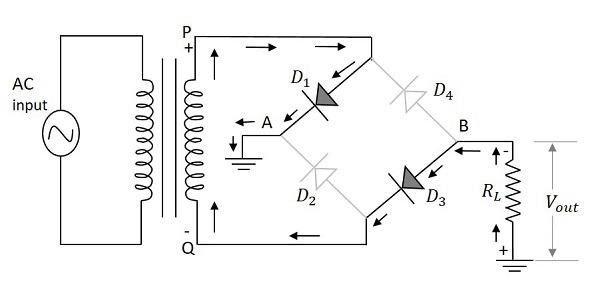
したがって、ダイオード $D_1$ そして $D_3$入力電源の正の半サイクル中に導通して、負荷抵抗に沿って出力を生成します。出力を生成するために2つのダイオードが機能するため、電圧はセンタータップ付き全波整流器の出力電圧の2倍になります。
入力電源の負の半サイクルが与えられると、ポイントPはポイントに対して負になります Q。これはダイオードを作ります$D_1$ そして $D_3$ 逆バイアス $D_2$ そして $D_4$順方向バイアス。これらの2つのダイオードは、負荷抵抗と直列になります。
次の図は、これを回路内の従来の電流フローとともに示しています。
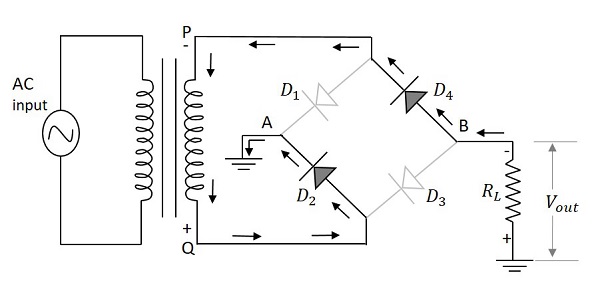
したがって、ダイオード $D_{2}$ そして $D_{4}$入力電源の負の半サイクル中に導通して、負荷抵抗に沿って出力を生成します。ここでも2つのダイオードが動作して出力電圧を生成します。電流は、入力の正の半サイクル中と同じ方向に流れます。
ブリッジFWRの波形
センタータップ全波整流器の入力波形と出力波形は次のとおりです。
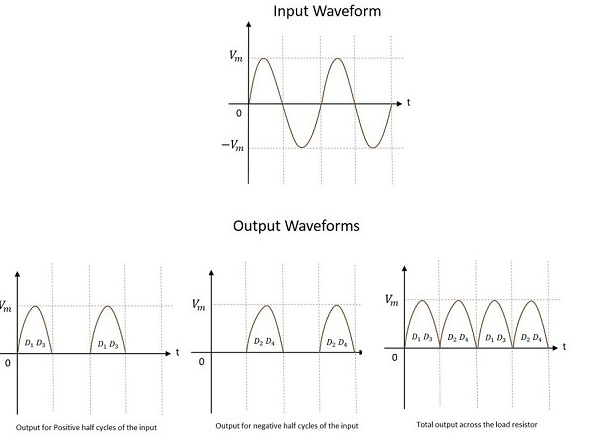
上の図から、正と負の両方の半サイクルで出力が得られていることがわかります。負荷抵抗の両端の出力がsame direction 両方の半サイクルで。
ピーク逆電圧
2つのダイオードがトランスの2次側に並列に接続されている場合は常に、トランスの両端の最大2次電圧が非導電性ダイオードに現れ、整流回路のPIVになります。従ってpeak inverse voltage は二次巻線の両端の最大電圧です。
$$PIV=V_m$$
利点
ブリッジ全波整流器には、次のような多くの利点があります。
- センタータップの必要はありません。
- DC出力電圧はセンタータッパーFWRの2倍です。
- ダイオードのPIVは、センタータッパーFWRの半分の値です。
- 回路の設計は、出力が優れているほど簡単です。
ここで、全波整流器の特性を分析してみましょう。
全波整流器の分析
全波整流回路を解析するために、入力電圧を仮定します。 $V_{i}$ なので、
$$V_{i}=V_m \sin \omega t$$
現在 $i_1$ 負荷抵抗を介して $R_L$ によって与えられます
$$i_1=I_m \sin \omega t \quad for \quad0 \leq \omega t \leq \pi$$
$$i_1=\quad0 \quad\quad\quad for \quad \pi \leq \omega t \leq 2\pi$$
どこ
$$I_m=\frac{V_m}{R_f+R_L}$$
$R_f$ オン状態でのダイオード抵抗です。
同様に、現在 $i_2$ ダイオードを流れる $D_2$ 負荷抵抗RLは次の式で与えられます。
$$i_2=\quad\:0 \quad\quad\quad for \quad 0 \leq \omega t \leq \pi$$
$$i_2=I_m \sin \omega t \quad for \quad\pi \leq \omega t \leq 2\pi$$
流れる総電流 $R_L$ 2つの電流の合計です $i_1$ そして $i_2$ すなわち
$$i=i_1+i_2$$
DCまたは平均電流
DC電流計が示す出力電流の平均値は次の式で与えられます。
$$I_{dc}=\frac{1}{2\pi} \int_{0}^{2\pi} i_1 \:d\left ( \omega t \right )+\frac{1}{2\pi}\int_{0}^{2\pi}i_2 \:d\left ( \omega t \right )$$
$$=\frac{1}{2\pi\int_{0}^{\pi}}I_m \sin \omega t \:d\left ( \omega t \right )+0+0+$$
$$\frac{1}{2\pi} \int_{0}^{2\pi}I_m \sin \omega t\:d\left ( \omega t \right ) $$
$$=\frac{I_m}{\pi}+ \frac{I_m}{\pi} =\frac{2I_m}{\pi}=0.636I_m$$
これは、半波整流器の値の2倍です。
DC出力電圧
負荷両端のDC出力電圧は次の式で与えられます。
$$V_{dc}=I_{dc}\times R_L = \frac{2I_mR_L}{\pi}=0.636I_mR_L$$
したがって、DC出力電圧は半波整流器の2倍です。
RMS電流
電流のRMS値は次の式で与えられます。
$$I_{rms}=\left [ \frac{1}{\pi}\int_{0}^{\pi} t^2 \:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
電流は2つの半分で2つの同じ形式であるため
$$=\left [ \frac{I_{m}^{2}}{\pi} \int_{0}^{\pi }\sin^2 \omega t\:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
$$=\frac{I_m}{\sqrt{2}}$$
整流器の効率
整流器の効率は次のように定義されます。
$$\eta=\frac{P_{dc}}{P_{ac}}$$
さて、
$$P_{dc}=\left (V_{dc} \right )^2/R_L=\left ( 2V_m/\pi \right )^2$$
そして、
$$P_{ac}=\left (V_{rms} \right )^2/R_L=\left (V_m/\sqrt{2} \right )^2$$
したがって、
$$\eta =\frac{P_{dc}}{P_{ac}}=\frac{\left (2V_m/\pi \right )^2}{\left ( V_m/\sqrt{2} \right )^2}=\frac{8}{\pi^2}$$
$$=0.812=81.2\%$$
整流器の効率は次のように計算できます-
DC出力電力、
$$P_{dc}=I_{dc}^{2}R_L=\frac{4I_{m}^{2}}{\pi^2}\times R_L$$
AC入力電力、
$$P_{ac}=I_{rms}^{2}\left (R_f+R_L \right )=\frac{I_{m}^{2}}{2}\left ( R_f+R_L \right )$$
したがって、
$$\eta=\frac{4I_{m}^{2}R_L/\pi^2}{I_{m}^{2}\left ( R_f+R_L \right )/2}=\frac{8}{\pi^2}\frac{R_L}{\left ( R_f+R_L \right )}$$
$$=\frac{0.812}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
したがって、パーセンテージ効率は
$$=\frac{0.812}{ 1+\left ( R_f+R_L \right )}$$
$$=81.2\% \quad if\: R_f=0$$
したがって、全波整流器の効率は半波整流器の2倍です。
リップルファクター
全波整流器の整流出力電圧のフォームファクタは、次の式で与えられます。
$$F=\frac{I_{rms}}{I_{dc}}=\frac{I_m/\sqrt{2}}{2I_m/\pi}=1.11$$
リップルファクター $\gamma$ (AC回路理論を使用して)として定義されます
$$\gamma =\left [ \left ( \frac{I_{rms}}{I_{dc}} \right )-1 \right ]^{\frac{1}{2}}=\left ( F^2 -1\right )^{\frac{1}{2}}$$
$$=\left [ \left ( 1.11 \right )^2 -1\right ]^\frac{1}{2}=0.48$$
これは、1.21であった半波整流器のリップル係数を大幅に改善したものです。
規制
DC出力電圧は次の式で与えられます。
$$V_{dc}=\frac{2I_mR_L}{\pi}=\frac{2V_mR_L}{\pi\left ( R_f+R_L \right )}$$
$$=\frac{2V_m}{\pi}\left [ 1-\frac{R_f}{R_f+R_L} \right ]=\frac{2V_m}{\pi}-I_{dc}R_f$$
変圧器利用率
半波整流器のTUFは0.287です
センタータップ整流器には2つの二次巻線があるため、センタータップ全波整流器のTUFは次のようになります。
$$\left ( TUF \right )_{avg}=\frac{P_{dc}}{V-A\:rating\:of\:a\:transformer}$$
$$=\frac{\left ( TUF \right )_p+\left ( TUF \right )_s+\left ( TUF \right )_s}{3}$$
$$=\frac{0.812+0.287+0.287}{3}=0.693$$
半波整流器と全波整流器
全波整流器のさまざまなパラメータのすべての値を調べた後、半波整流器と全波整流器の機能を比較対照してみましょう。
| 条項 | 半波整流器 | センタータップFWR | ブリッジFWR |
|---|---|---|---|
| ダイオードの数 | $1$ | $2$ | $4$ |
| 変圧器のタッピング | $No$ | $Yes$ | $No$ |
| ピーク逆電圧 | $V_m$ | $2V_m$ | $V_m$ |
| 最大効率 | $40.6\%$ | $81.2\%$ | $81.2\%$ |
| 平均/ DC電流 | $I_m/\pi$ | $2I_m/\pi$ | $2I_m/\pi$ |
| DC電圧 | $V_m/\pi$ | $2V_m/\pi$ | $2V_m/\pi$ |
| RMS電流 | $I_m/2$ | $I_m/\sqrt{2}$ | $I_m/\sqrt{2}$ |
| リップルファクター | $1.21$ | $0.48$ | $0.48$ |
| 出力周波数 | $f_{in}$ | $2f_{in}$ | $2f_{in}$ |
電源ブロック図は、整流回路の後にフィルタ回路が必要であることを明確に説明しています。整流器は、脈動する交流を一方向にのみ流れる直流に変換するのに役立ちます。これまで、さまざまなタイプの整流回路を見てきました。
これらすべての整流回路の出力には、リップル係数が含まれています。また、半波整流器のリップル係数が全波整流器のリップル係数よりも大きいことも確認しました。
なぜフィルターが必要なのですか?
信号のリップルは、AC成分の存在を示します。純粋なDC出力を得るには、このACコンポーネントを完全に削除する必要があります。だから、私たちはその回路が必要ですsmoothens 整流された出力を純粋なDC信号に変換します。
A filter circuit は、整流された出力に存在するAC成分を除去し、DC成分が負荷に到達できるようにするものです。
次の図は、フィルタ回路の機能を示しています。

フィルタ回路は、インダクタとコンデンサの2つの主要コンポーネントを使用して構成されています。ベーシックエレクトロニクスのチュートリアルですでに勉強しました
インダクタは dc とブロック ac。
コンデンサは ac とブロック dc。
これらの2つのコンポーネントを使用して、いくつかのフィルターを作成してみましょう。
シリーズインダクターフィルター
インダクタはDCを許可し、ACをブロックするため、 Series Inductor Filterインダクタを整流器と負荷の間に直列に接続することで構築できます。下の図は、直列インダクタフィルタの回路を示しています。
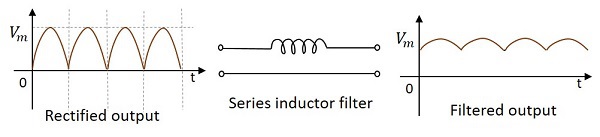
このフィルタを通過するときに整流された出力であるインダクタは、純粋なDCを提供するために、信号に存在するAC成分をブロックします。これは単純な一次フィルターです。
シャントコンデンサフィルター
コンデンサはACを通過させ、DCをブロックするため、 Shunt Capacitor Filter 次の図に示すように、シャントに接続されたコンデンサを使用して構築できます。
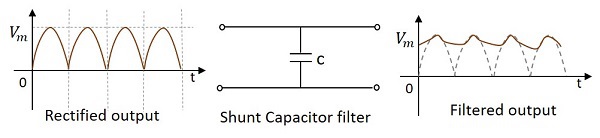
このフィルターを通過するときに整流された出力である信号に存在するAC成分は、AC成分を可能にするコンデンサーを介して接地されます。信号に存在する残りのDC成分は、出力で収集されます。
上記のフィルタタイプは、インダクタまたはコンデンサを使用して構成されています。それでは、両方を使用して、より良いフィルターを作成してみましょう。これらは組み合わせフィルターです。
LCフィルター
インダクタとコンデンサの両方の効率を使用できる場合に、より良い出力を得るために、インダクタとコンデンサの両方を使用してフィルタ回路を構築できます。下図にLCフィルタの回路図を示します。
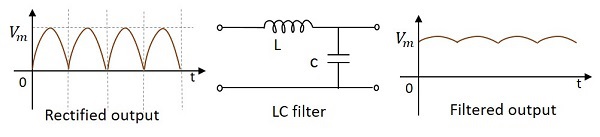
この回路に与えられると整流された出力であるインダクタは、DC成分がそれを通過することを可能にし、信号のAC成分をブロックします。さて、その信号から、純粋なDC出力が得られるように、存在する場合はさらにいくつかのACコンポーネントが接地されます。
このフィルターは、 Choke Input Filter入力信号が最初にインダクタに入るとき。このフィルターの出力は、以前のフィルターよりも優れています。
Π-フィルター(Piフィルター)
これは、非常に一般的に使用されている別のタイプのフィルター回路です。入力にコンデンサがあるため、Capacitor Input Filter。ここでは、2つのコンデンサと1つのインダクタがπ型ネットワークの形で接続されています。並列のコンデンサ、次に直列のインダクタ、続いて並列の別のコンデンサがこの回路を構成します。
必要に応じて、必要に応じて、いくつかの同一のセクションをこれに追加することもできます。下の図は、$\pi$ フィルタ (Pi-filter)。
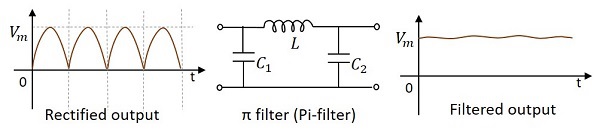
Piフィルターの働き
この回路では、並列にコンデンサがあり、次に直列にインダクタがあり、次に並列に別のコンデンサがあります。
Capacitor C1−このフィルタコンデンサは、DC信号に対して高いリアクタンスを提供し、AC信号に対して低いリアクタンスを提供します。信号に存在するAC成分を接地した後、信号はインダクタに渡されてさらにフィルタリングされます。
Inductor L−このインダクタは、コンデンサC 1を通過することができた場合、ACコンポーネントをブロックしながら、DCコンポーネントに対して低いリアクタンスを提供します。
Capacitor C2 −これで、このコンデンサを使用して信号がさらに平滑化され、インダクタがブロックできなかった信号に存在するAC成分が許容されるようになります。
したがって、負荷で目的の純粋なDC出力を取得します。
電源システムの負荷前の次の最後の段階は、レギュレーター部分です。ここで、レギュレーターとは何か、そしてそれが何をするのかを理解してみましょう。
電力の制御と変換を扱う電子機器の部分は、次のように呼ぶことができます。 Power Electronics。レギュレーターは、パワー出力を制御するため、パワーエレクトロニクスに関して重要なデバイスです。
レギュレーターの必要性
入力電圧の変動や負荷電流の変動に関係なく、電源が一定の出力電圧を生成するためには、電圧レギュレータが必要です。
A voltage regulatorは、負荷によって引き出される入力電圧の変動や電流の変動の代わりに、一定の出力電圧を維持するデバイスです。次の画像は、実際のレギュレーターがどのように見えるかを示しています。

レギュレーターの種類
レギュレーターは、その動作と接続のタイプに応じて、さまざまなカテゴリーに分類できます。
Depending upon the type of regulation、レギュレーターは主にラインレギュレーターと負荷レギュレーターの2種類に分けられます。
Line Regulator −入力ラインの変動にもかかわらず、出力電圧を一定に調整するレギュレータは、次のように呼ばれます。 Line regulator。
Load Regulator −出力での負荷の変動にもかかわらず、出力電圧を一定に調整するレギュレータは、次のように呼ばれます。 Load regulator。
Depending upon the type of connection、電圧レギュレータには2つのタイプがあります。彼らです
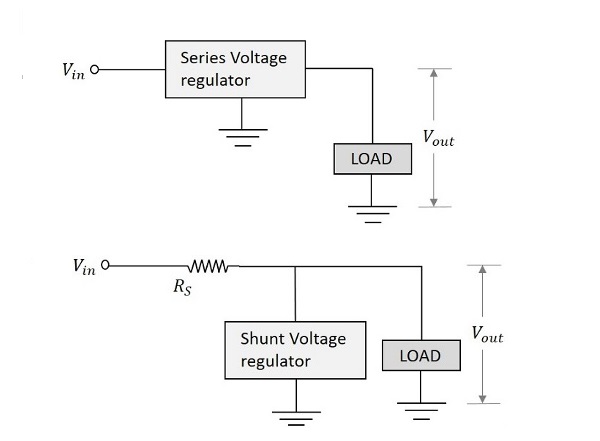
- 直列電圧レギュレータ
- シャント電圧レギュレータ
回路内での配置は次の図のようになります。
他の重要なレギュレータータイプを見てみましょう。
ツェナー電圧レギュレータ
ツェナー電圧レギュレータは、出力電圧を調整するためにツェナーダイオードを使用するものです。ツェナーダイオードの詳細については、BASICELECTRONICSチュートリアルですでに説明しました。
ツェナーダイオードが故障時または Zener region、その両端の電圧は実質的に constant のために large change of currentそれを通して。この特性により、ツェナーダイオードはgood voltage regulator。
次の図は、単純なツェナーレギュレータの画像を示しています。
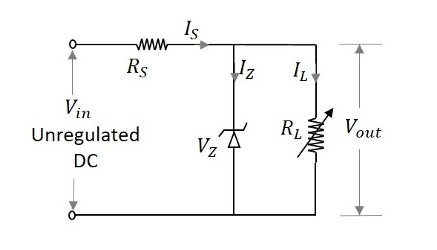
印加入力電圧 $V_i$ ツェナー電圧を超えて増加した場合 $V_z$、次にツェナーダイオードはブレークダウン領域で動作し、負荷の両端に一定の電圧を維持します。直列制限抵抗$R_s$ 入力電流を制限します。
ツェナー電圧レギュレータの動作
ツェナーダイオードは、負荷変動や入力電圧変動にもかかわらず、その両端の電圧を一定に保ちます。したがって、ツェナー電圧レギュレータの動作を理解するために4つのケースを検討できます。
Case 1 −負荷電流の場合 $I_L$ 増加すると、ツェナーダイオードを流れる電流が増加します $I_Z$ 直列抵抗を流れる電流を維持するために減少します $R_S$絶え間ない。出力電圧Voは、入力電圧Viと直列抵抗両端の電圧に依存します。$R_S$。
これは次のように書くことができます
$$V_o=V_{in}-IR_{s}$$
どこ $I$は一定です。したがって、$V_o$ また、一定のままです。
Case 2 −負荷電流の場合 $I_L$ 減少すると、ツェナーダイオードを流れる電流が減少します $I_Z$ 現在のように増加します $I_S$RS直列抵抗を介して一定のままです。現在の$I_Z$ ツェナーダイオードを介して増加し、一定の出力電圧を維持します $V_Z$、負荷電圧を一定に保ちます。
Case 3 −入力電圧の場合 $V_i$ 増加し、次に電流 $I_S$直列抵抗を介してRSが増加します。これにより、抵抗の両端の電圧降下が増加します。$V_S$増加します。ツェナーダイオードを流れる電流は$I_Z$ これに伴い、ツェナーダイオード両端の電圧が上昇します $V_Z$ 出力負荷電圧を一定に保ちながら、一定に保ちます。
Case 4 −入力電圧が低下すると、直列抵抗を流れる電流が減少し、ツェナーダイオードを流れる電流になります。 $I_Z$減少します。しかし、ツェナーダイオードはその特性により出力電圧を一定に保ちます。
ツェナー電圧レギュレータの制限
ツェナー電圧レギュレータにはいくつかの制限があります。彼らは-
- 大きな負荷電流に対しては効率が低下します。
- ツェナーインピーダンスは出力電圧にわずかに影響します。
したがって、ツェナー電圧レギュレータは低電圧アプリケーションに効果的であると考えられています。それでは、トランジスタを使用して作られた他のタイプの電圧レギュレータを見てみましょう。
トランジスタシリーズ電圧レギュレータ
このレギュレータには、ツェナーレギュレータと直列にトランジスタがあり、両方とも負荷に並列になっています。トランジスタは、出力電圧を一定に保つために、コレクタエミッタ電圧を調整する可変抵抗器として機能します。下の図は、トランジスタの直列電圧レギュレータを示しています。
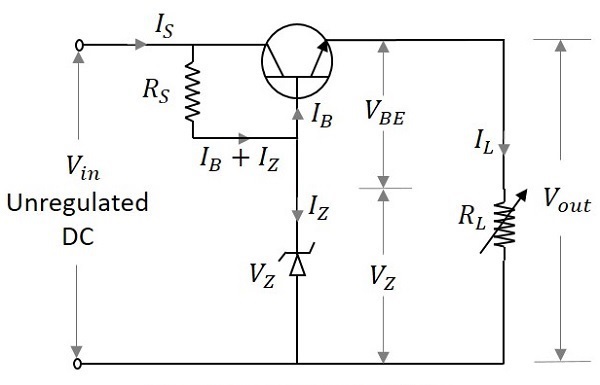
入力動作条件により、トランジスタのベースを流れる電流が変化します。これは、トランジスタのベースエミッタ接合の両端の電圧に影響します$V_{BE}$。出力電圧はツェナー電圧によって維持されます$V_Z$これは一定です。両方が等しく維持されるため、入力電源の変化はエミッタベース電圧の変化によって示されます$V_{BE}$。
したがって、出力電圧Voは次のように理解できます。
$$V_O=V_Z+V_{BE}$$
トランジスタシリーズ電圧レギュレータの動作
入力と負荷の変動については、直列電圧レギュレータの動作を考慮する必要があります。入力電圧を上げると、出力電圧も上がります。しかし、これにより、コレクタベース接合の両端の電圧が発生します$V_{BE}$ ツェナー電圧として減少する $V_Z$一定のまま。エミッタコレクタ領域全体の抵抗が増加すると、伝導は減少します。これにより、コレクタエミッタ接合VCEの両端の電圧がさらに上昇し、出力電圧が低下します。$V_O$。これは、入力電圧が低下した場合も同様です。
負荷が変化したとき、つまり負荷の抵抗が減少すると、負荷電流が増加します $I_L$、出力電圧 $V_O$ 減少し、エミッタベース電圧が増加します $V_{BE}$。
エミッタベース電圧の増加に伴い $V_{BE}$伝導が増加し、エミッタコレクタ抵抗が減少します。これにより、入力電流が増加し、負荷抵抗の減少が補償されます。これは、負荷電流が増加した場合も同様です。
トランジスタシリーズ電圧レギュレータの制限
トランジスタシリーズ電圧レギュレータには、次の制限があります-
- 電圧 $V_{BE}$ そして $V_Z$ 温度上昇の影響を受けます。
- 大電流を適切に調整することはできません。
- 消費電力が大きい。
- 消費電力が大きい。
- 効率が悪い。
これらの制限を最小限に抑えるために、トランジスタシャントレギュレータが使用されます。
トランジスタシャント電圧レギュレータ
トランジスタシャントレギュレータ回路は、入力と直列に抵抗を接続し、そのベースとコレクタが両方とも負荷と並列に調整するツェナーダイオードによって接続されているトランジスタを接続することによって形成されます。下の図は、トランジスタシャントレギュレータの回路図を示しています。
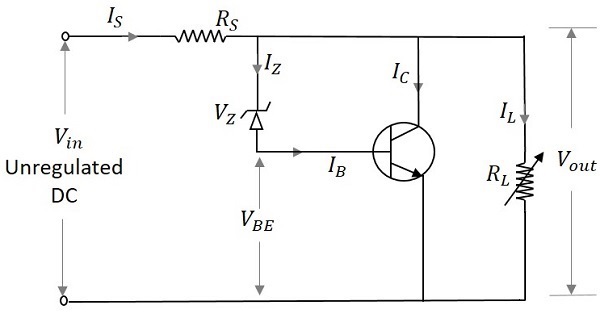
トランジスタシャント電圧レギュレータの動作
入力電圧が上昇すると、 $V_{BE}$ そして $V_O$また増加します。しかし、これは最初に起こります。実はいつ$V_{in}$ 増加し、現在 $I_{in}$また増加します。この電流がRSを流れると、電圧降下が発生します$V_S$ 直列抵抗の両端で、これも $V_{in}$。しかし、これは$V_o$減少する。今、この減少$V_o$最初の増加を補正して、一定に維持します。したがって、$V_o$一定に保たれます。代わりに出力電圧が低下すると、逆のことが起こります。
負荷抵抗が低下すると、出力電圧が低下するはずです。 $V_o$。負荷を流れる電流が増加します。これにより、トランジスタのベース電流とコレクタ電流が減少します。電流が大きく流れると、直列抵抗の両端の電圧が低くなります。入力電流は一定になります。
表示される出力電圧は、印加電圧の差になります $V_i$ および直列電圧降下 $V_s$。したがって、出力電圧は最初の減少を補うために増加し、したがって一定に維持されます。負荷抵抗が増加すると、逆のことが起こります。
ICレギュレーター
電圧レギュレータは、現在、集積回路(IC)の形で入手できます。これらは略してICレギュレータと呼ばれます。
ICレギュレータは、通常のレギュレータのような機能に加えて、熱補償、短絡保護、サージ保護などの特性をデバイスに組み込んでいます。
ICレギュレータの種類
ICレギュレータには次のタイプがあります-
- 固定正電圧レギュレータ
- 固定負電圧レギュレータ
- 調整可能な電圧レギュレータ
- デュアルトラッキング電圧レギュレータ
それでは、それらについて詳しく説明しましょう。
固定正電圧レギュレータ
これらのレギュレータの出力は特定の値に固定されており、値は正です。つまり、提供される出力電圧は正の電圧です。
最も使用されているシリーズは7800シリーズで、ICはIC 7806、IC 7812、IC 7815などのようになり、出力電圧としてそれぞれ+ 6v、+ 12v、+ 15vを提供します。次の図は、固定の10v正の安定化出力電圧を提供するように接続されたIC7810を示しています。
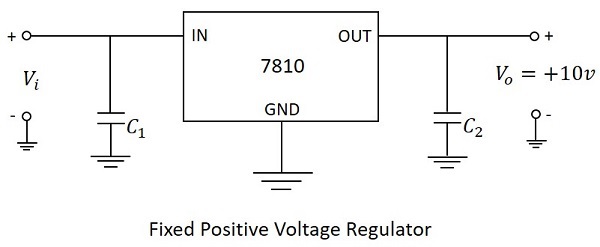
上図では、入力コンデンサ $C_1$ 不要な発振や出力コンデンサを防止するために使用されます $C_2$ 過渡応答を改善するためのラインフィルターとして機能します。
固定負電圧レギュレータ
これらのレギュレータの出力は特定の値に固定されており、値は負です。つまり、提供される出力電圧は負の電圧です。
最も使用されているシリーズは7900シリーズで、ICはIC 7906、IC 7912、IC 7915などのようになり、出力電圧としてそれぞれ-6v、-12v、-15vを提供します。次の図は、固定の10v負の安定化出力電圧を提供するように接続されたIC7910を示しています。
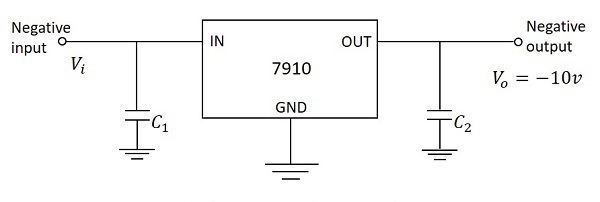
上図では、入力コンデンサ $C_1$ 不要な発振や出力コンデンサを防止するために使用されます $C_2$ 過渡応答を改善するためのラインフィルターとして機能します。
調整可能な電圧レギュレータ
調整可能な電圧レギュレータには、IN、OUT、ADJの3つの端子があります。入力端子と出力端子は共通ですが、調整可能な端子には可変抵抗があり、出力を広い範囲で変化させることができます。
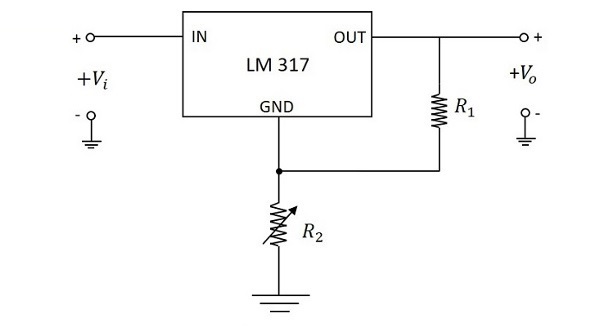
上の図は、一般的に使用されているLM317調整可能ICレギュレーターを駆動する非安定化電源を示しています。LM 317は、3端子の正の調整可能な電圧レギュレータであり、1.25v〜37vの調整可能な出力範囲で1.5Aの負荷電流を供給できます。
デュアルトラッキング電圧レギュレータ
分割電源電圧が必要な場合は、デュアルトラッキングレギュレータが使用されます。これらは等しい正と負の出力電圧を提供します。たとえば、RC4195ICは+ 15vおよび-15vのDC出力を提供します。これには、正の入力が+ 18vから+ 30vまで変化し、負の入力が-18vから-30vまで変化するなど、2つの調整されていない入力電圧が必要です。
上の画像は、デュアルトラッキングRC4195ICレギュレーターを示しています。調整可能なデュアルタッキングレギュレーターも利用可能で、その出力は2つの定格制限間で変化します。
これまでに説明したトピックは、電源ユニットのさまざまなセクションを表しています。これらすべてのセクションが一緒になってLinear Power Supply。これは、入力AC電源からDCを取得する従来の方法です。
リニア電源
リニア電源(LPS)は、直列抵抗で多くの熱を放散して、リップルとノイズの少ない出力電圧を調整する安定化電源です。このLPSには多くのアプリケーションがあります。
リニア電源は、出力電圧を調整するためにより大きな半導体デバイスを必要とし、より多くの熱を生成するため、エネルギー効率が低下します。リニア電源の過渡応答時間は他の電源よりも最大100倍速く、これは特定の専門分野で非常に重要です。
LPSの利点
- 電源は連続しています。
- 回路はシンプルです。
- これらは信頼できるシステムです。
- このシステムは、負荷の変化に動的に応答します。
- 回路抵抗は、出力電圧を調整するために変更されます。
- コンポーネントは線形領域で動作するため、ノイズは低くなります。
- 出力電圧のリップルは非常に小さいです。
LPSのデメリット
- 使用される変圧器はより重くて大きいです。
- 熱放散はもっとあります。
- リニア電源の効率は40〜50%です
- LPS回路では、電力が熱の形で浪費されます。
- 単一の出力電圧が得られます。
リニア電源のさまざまな部分については、すでに説明しました。リニア電源のブロック図は次の図のようになります。

上記の欠点にもかかわらず、リニア電源は低ノイズアンプ、テスト機器、制御回路で広く使用されています。さらに、データ収集や信号処理にも使用されます。
簡単な調整が必要で、効率が問題にならないすべての電源システムには、LPS回路が使用されます。電気的ノイズが低いため、LPSは敏感なアナログ回路に電力を供給するために使用されます。ただし、リニア電源システムの欠点を克服するために、スイッチモード電源(SMPS)が使用されます。
スイッチモード電源(SMPS)
効率の低下、リップルを低減するための大きな値のコンデンサの必要性、重くて高価な変圧器などのLPSの欠点は、次の実装によって克服されます。 Switched Mode Power Supplies。
SMPSの動作は、LPSで使用されるトランジスタが電圧降下を制御するために使用され、SMPSのトランジスタが controlled switch。
ワーキング
SMPSの動作は次の図で理解できます。
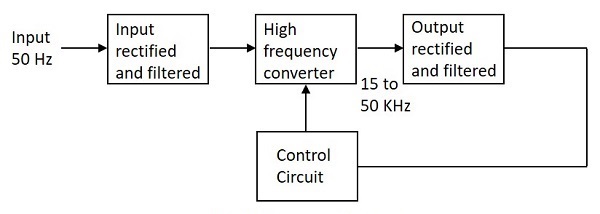
SMPS回路の各段階で何が起こるかを理解してみましょう。
入力ステージ
AC入力電源信号50Hzは、トランスを使用せずに整流器とフィルタ回路の組み合わせに直接与えられます。この出力には多くの変動があり、入力の変動を処理するには、コンデンサの静電容量値を高くする必要があります。この調整されていないDCは、SMPSの中央スイッチングセクションに供給されます。
スイッチングセクション
このセクションでは、パワートランジスタやMOSFETなどの高速スイッチングデバイスを使用します。このデバイスは、バリエーションに応じてオンとオフを切り替え、この出力はこのセクションにあるトランスの1次側に与えられます。ここで使用されているトランスは、60 Hzの電源に使用されているものとは異なり、はるかに小型で軽量です。これらは非常に効率的であるため、電力変換率が高くなります。
出力段
スイッチングセクションからの出力信号は、必要なDC電圧を得るために、再び整流およびフィルタリングされます。これは安定化された出力電圧であり、フィードバック回路である制御回路に与えられます。最終的な出力は、フィードバック信号を考慮した後に取得されます。
コントロールユニット
このユニットは、多くのセクションを持つフィードバック回路です。次の図から、これについて明確に理解しましょう。
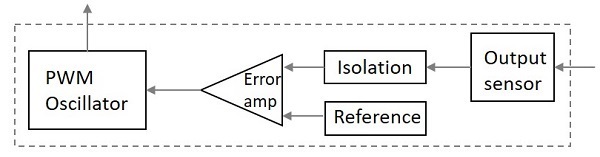
上の図は、コントロールユニットの内部を説明しています。出力センサーは信号を感知し、それをコントロールユニットに結合します。信号は他のセクションから分離されているため、突然のスパイクが回路に影響を与えることはありません。基準電圧は、信号を必要な信号レベルと比較するコンパレータであるエラーアンプへの信号とともに1つの入力として与えられます。
チョッピング周波数を制御することにより、最終的な電圧レベルが維持されます。これは、エラーアンプに与えられた入力を比較することによって制御されます。エラーアンプの出力は、チョッピング周波数を上げるか減らすかを決定するのに役立ちます。PWM発振器は、標準のPWM波固定周波数を生成します。
次の図を見ると、SMPSの完全な機能についてより良いアイデアを得ることができます。
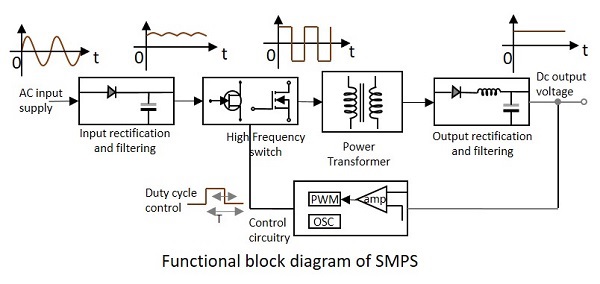
SMPSは主に、電圧の切り替えがまったく問題にならず、システムの効率が本当に重要な場合に使用されます。SMPSに関して注意すべき点がいくつかあります。彼らです
SMPS回路はスイッチングによって動作するため、電圧は連続的に変化します。
スイッチングデバイスは、飽和モードまたはカットオフモードで動作します。
出力電圧は、フィードバック回路のスイッチング時間によって制御されます。
スイッチング時間は、デューティサイクルを調整することによって調整されます。
SMPSは、余剰電力を熱として放散するのではなく、入力を継続的に切り替えて出力を制御するため、効率が高くなります。
短所
SMPSには、次のようないくつかの欠点があります。
- 高周波スイッチングによるノイズが存在します。
- 回路は複雑です。
- 電磁干渉を発生させます。
利点
SMPSの利点は次のとおりです。
- 効率は80〜90%と高いです
- より少ない発熱; 電力の浪費が少なくなります。
- 電源メインへの高調波フィードバックが減少しました。
- デバイスはコンパクトでサイズが小さいです。
- 製造コストが削減されます。
- 必要な数の電圧を提供するための準備。
アプリケーション
SMPSには多くの用途があります。これらは、コンピューターのマザーボード、携帯電話の充電器、HVDC測定、バッテリー充電器、中央配電、自動車、家庭用電化製品、ラップトップ、セキュリティシステム、宇宙ステーションなどで使用されます。
SMPSの種類
SMPSは、安定化されていないDCまたはAC電圧から安定化されたDC出力電圧を取得するように設計されたスイッチモード電源回路です。SMPSには主に次の4つのタイプがあります。
- DC-DCコンバーター
- AC-DCコンバーター
- フライバックコンバーター
- フォワードコンバーター
入力部のAC-DC変換部は、AC-DCコンバータとDC-DCコンバータの違いを生みます。フライバックコンバータは、低電力アプリケーションに使用されます。また、SMPSタイプには、要件に応じて出力電圧を増減するバックコンバータとブーストコンバータがあります。他のタイプのSMPSには、自励発振フライバックコンバーター、バックブーストコンバーター、Cuk、Sepicなどがあります。