DC電流計
電流は電荷の流量です。この電荷が一方向にのみ流れる場合、結果として生じる電流は直流(DC)と呼ばれます。と呼ばれる直流を測定するために使用される機器DC ammeter。
永久磁石ムービングコイル(PMMC)検流計と並列に抵抗を配置すると、組み合わせ全体がDC電流計として機能します。DC電流計で使用される並列抵抗は、シャント抵抗または単にshunt。大きな値のDC電流を測定するには、この抵抗の値を小さくする必要があります。
ザ・ circuit diagram DC電流計の概要を下図に示します。
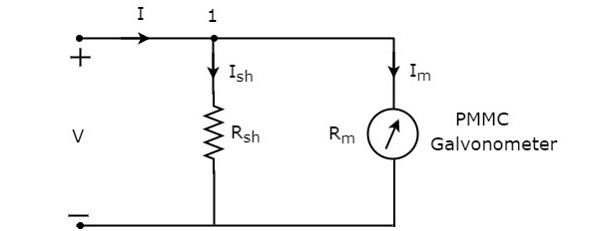
これを配置する必要があります DC ammeterDC電流が測定される電気回路の分岐と直列に接続されています。並列に接続されている要素間の電圧は同じです。したがって、シャント抵抗の両端の電圧$ R_ {sh} $と検流計の抵抗の両端の電圧$ R_ {m} $は同じです。これは、これら2つの要素が上記の回路で並列に接続されているためです。Mathematically、次のように書くことができます
$$ I_ {sh} R_ {sh} = I_ {m} R_ {m} $$
$ \ Rightarrow R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}} $ (式1)
ザ・ KCL equation ノード1には
$$-I + I_ {sh} + I_ {m} = 0 $$
$$ \ Rightarrow I_ {sh} = I-I_ {m} $$
Substitute 式1の$ I_ {sh} $の値。
$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}} $ (式2)
式2の右辺にある分母の項で一般的な$ I_ {m} $を考えてみましょう。
$$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {m}(\ frac {1} {I_ {m}}-1)} $$
$ \ Rightarrow R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}}-1} $ (式3)
どこ、
$ R_ {sh} $はシャント抵抗です
$ R_ {m} $は検流計の内部抵抗です
$ I $は、測定される直流電流の合計です。
$ I_ {m} $はフルスケールのたわみ電流です
測定される総直流電流$ I $と検流計のフルスケールたわみ電流$ I_ {m} $の比率は次のように知られています。 multiplying factor, m。数学的には、次のように表すことができます。
$ m = \ frac {I} {I_ {m}} $ (式4)
$ R_ {sh} = \ frac {R_ {m}} {m-1} $ (式5)
私たちは見つけることができます value of shunt resistance 利用可能なデータに基づいて、式2または式5のいずれかを使用します。
マルチレンジDC電流計
前のセクションでは、PMMC検流計と並列に抵抗を配置することによって得られるDC電流計について説明しました。このDC電流計は、particular range 直流の。
の直流電流を測定するためにDC電流計を使用したい場合 multiple ranges、次に、単一の抵抗器の代わりに複数の並列抵抗器を使用する必要があり、この抵抗器の組み合わせ全体がPMMC検流計と並列になります。ザ・circuit diagram マルチレンジDC電流計の概要を下図に示します。
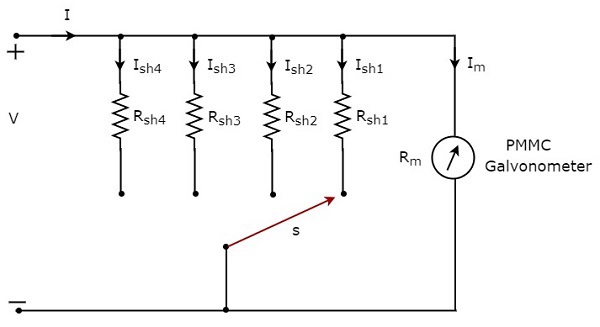
このマルチレンジDC電流計を、必要な範囲の直流を測定する電気回路の分岐と直列に配置します。必要な電流範囲は、スイッチsをそれぞれのシャント抵抗に接続することによって選択されます。
$ m_ {1}、m_ {2}、m_ {3} $、$ m_ {4} $を multiplying factors合計直流電流をそれぞれ$ I_ {1}、I_ {2}、I_ {3} $、および$ I_ {4} $として測定すると見なした場合のDC電流計の値。以下は、各倍率に対応する式です。
$$ m_ {1} = \ frac {I_ {1}} {I_ {m}} $$
$$ m_ {2} = \ frac {I_ {2}} {I_ {m}} $$
$$ m_ {3} = \ frac {I_ {3}} {I_ {m}} $$
$$ m_ {4} = \ frac {I_ {4}} {I_ {m}} $$
上記の回路には4つあります shunt resistors、$ R_ {sh1}、R_ {sh2}、R_ {sh2} $、および$ R_ {sh4} $。これらの4つの抵抗に対応する式は次のとおりです。
$$ R_ {sh1} = \ frac {R_ {m}} {m_ {1} -1} $$
$$ R_ {sh2} = \ frac {R_ {m}} {m_ {2} -1} $$
$$ R_ {sh3} = \ frac {R_ {m}} {m_ {3} -1} $$
$$ R_ {sh4} = \ frac {R_ {m}} {m_ {4} -1} $$
上記の式は、各シャント抵抗の抵抗値を見つけるのに役立ちます。