DCブリッジ
DC bridgesDC電圧信号のみで操作できます。DCブリッジは、ブリッジに存在する未知の抵抗の値を測定するのに役立ちます。ホイートストンブリッジはDCブリッジの一例です。
さて、について話し合いましょう Wheatstone’s Bridge 未知の抵抗値を見つけるために。
ホイートストンブリッジ
ホイートストンブリッジは単純なDCブリッジで、主に4本のアームがあります。これらの4つのアームはひし形または正方形の形状を形成し、各アームは1つの抵抗で構成されます。
未知の抵抗の値を見つけるには、検流計とDC電圧源が必要です。したがって、これら2つの一方はホイートストンブリッジの一方の対角線に配置され、もう一方はホイートストンブリッジのもう一方の対角線に配置されます。
ホイートストンブリッジは、中程度の抵抗の値を測定するために使用されます。ザ・circuit diagram ホイートストンブリッジの概要を下図に示します。
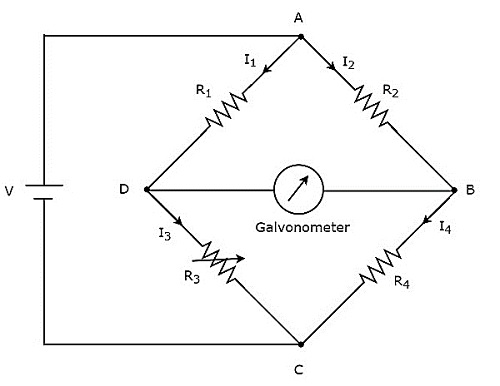
上記の回路では、アームAB、BC、CD、およびDAが一緒になって rhombusまたは正方形の形。これらは、それぞれ抵抗$ R_ {2} $、$ R_ {4} $、$ R_ {3} $、および$ R_ {1} $で構成されています。これらの抵抗アームを流れる電流をそれぞれ$ I_ {2} $、$ I_ {4} $、$ I_ {3} $、$ I_ {1} $とし、これらの電流の方向を図に示します。
対角アームDBとACは、それぞれVボルトの検流計とDC電圧源で構成されています。ここで、抵抗$ R_ {3} $は標準の可変抵抗であり、抵抗$ R_ {4} $は未知の抵抗です。私たちはできるbalance the bridge、抵抗器の抵抗値を変えることにより、$ R_ {3} $。
上記のブリッジ回路は、対角アームDBに電流が流れていないときにバランスが取れています。つまり、no deflection 検流計で、ブリッジのバランスが取れているとき。
次の場合、ブリッジはバランスが取れます two conditions 満足しています。
アームADの両端の電圧はアームABの両端の電圧に等しくなります。すなわち、
$$ V_ {AD} = V_ {AB} $$
$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $式1
アームDCの両端の電圧は、アームBCの両端の電圧に等しくなります。すなわち、
$$ V_ {DC} = V_ {BC} $$
$ \ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4} $式2
上記の2つのバランス条件から、次のようになります。 two conclusions.
アームADを流れる電流はアームDCの電流と等しくなります。すなわち、
$$ I_ {1} = I_ {3} $$
アームABを流れる電流は、アームBCの電流と等しくなります。すなわち、
$$ I_ {2} = I_ {4} $$
式1と式2の比率を取ります。
$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $式3
式3の$ I_ {1} = I_ {3} $と$ I_ {2} = I_ {4} $を代入します。
$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$
$$ \ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$
$$ \ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
上記の式に抵抗$ R_ {1} $、$ R_ {2} $、$ R_ {3} $の既知の値を代入すると、次の式が得られます。 value of resistor,$R_{4}$。