クイックガイド

任意の量を測定するために使用される機器は、測定機器として知られています。このチュートリアルでは、主にelectronic instruments、電気量またはパラメータの測定に役立ちます。

以下は、最も一般的に使用される電子楽器です。

• Voltmeter
• Ammeter
• Ohmmeter
• Multimeter

それでは、これらの楽器について簡単に説明しましょう。

電圧計

名前が示すように、 voltmeter電気回路の任意の2点間の電圧を測定する測定器です。電圧計には、DC電圧計とAC電圧計の2種類があります。

DC電圧計は、電気回路の任意の2点のDC電圧を測定しますが、AC電圧計は、電気回路の任意の2点のAC電圧を測定します。の例practical DC voltmeter 下図に示します。

上図に示すDC電圧計は $(0-100)V$ DC voltmeter。したがって、0ボルトから10ボルトまでのDC電圧を測定するために使用できます。

電流計

名前が示すように、 ammeter電気回路の任意の2点を流れる電流を測定する測定器です。電流計には、DC電流計とAC電流計の2種類があります。

DC電流計は、電気回路の任意の2点を流れるDC電流を測定します。一方、AC電流計は、電気回路の任意の2点を流れるAC電流を測定します。の例practical AC ammeter 下の図に示されています-

上図に示すAC電流計は $(0-100)A \:$ AC ammeter。したがって、ゼロアンペアから100アンペアまでのAC電流を測定するために使用できます。

抵抗計

Ohmmeter電気回路の任意の2点間の抵抗値を測定するために使用されます。また、未知の抵抗の値を見つけるために使用することもできます。抵抗計には、直列抵抗計とシャント抵抗計の2種類があります。

直列型抵抗計では、値が不明で測定対象の抵抗器を抵抗計と直列に接続する必要があります。測定に便利ですhigh values of resistances。

シャントタイプのオーム計では、値が不明で測定対象の抵抗器をオーム計と並列（シャント）に接続する必要があります。測定に便利ですlow values of resistances。

の例 practical shunt ohmmeter上図に示します。上の図に示されている抵抗計は$(0-100)\Omega$ shunt ohmmeter。したがって、0オームから100オームまでの抵抗値を測定するために使用できます。

マルチメータ

Multimeterは、電圧、電流、抵抗などの量を一度に1つずつ測定するために使用される電子機器です。これは、DCおよびAC電圧、DCおよびAC電流、およびいくつかの範囲の抵抗を測定するために使用できます。実用的なマルチメータを次の図に示します-

図に示すように、このマルチメータは、さまざまな高抵抗、低抵抗、DC電圧、AC電圧、DC電流、およびAC電流を測定するために使用できます。これらの量のそれぞれの異なるスケールと値の範囲は、上の図にマークされています。

この章で検討した機器は indicating type instruments、これらの機器のポインタが偏向し、特定の値を指しているため。これらの電子測定器については、後の章で詳しく説明します。

測定器の性能を知るのに役立ち、任意の量またはパラメータの測定に役立つ測定器の特性は、次のように知られています。 Performance Characteristics。

性能特性の種類

機器の性能特性は次のように分類できます。 two types。

• 静的特性
• 動的特性

ここで、これら2つのタイプの特性について1つずつ説明します。

静的特性

量またはパラメータ測定器の特性 do not vary時間に関しては静的特性と呼ばれます。場合によっては、これらの量またはパラメーターは時間に対してゆっくりと変化することがあります。以下はのリストですstatic characteristics。

• Accuracy
• Precision
• Sensitivity
• Resolution
• 静的エラー

それでは、これらの静的特性について1つずつ説明していきましょう。

正確さ

楽器の指示値$ A_ {i} $と真の値$ A_ {t} $の代数的差異は次のように知られています。 accuracy。数学的には、次のように表すことができます。

$$精度= A_ {i} -A_ {t} $$

精度という用語は、機器の指示値$ A_ {i} $が真の値$ A_ {t} $にどれだけ近いかを示します。

静的エラー

時間に対して変化しない数量の真の値$ A_ {t} $と楽器の指示値$ A_ {i} $の差は次のように知られています。 static error、$ e_ {s} $。数学的には、次のように表すことができます。

$$ e_ {s} = A_ {t} -A_ {i} $$

静的エラーという用語は、機器の不正確さを意味します。静的エラーがパーセンテージで表される場合、それは呼び出されますpercentage of static error。数学的には、次のように表すことができます。

$$ \％e_ {s} = \ frac {e_ {s}} {A_ {t}} \ times 100 $$

代入すると、上記の式の右辺の$ e_ {s} $の値-

$$ \％e_ {s} = \ frac {A_ {t} -A_ {i}} {A_ {t}} \ times 100 $$

どこ、

$ \％e_ {s} $は、静的エラーのパーセンテージです。

精度

同じ状況で同じ量を何度も測定するために使用したときに同じ値を繰り返し示す場合、その測定器は高いと言えます。 precision。

感度

出力の変化の比率、入力の特定の変化に対する計測器の$ \ Delta A_ {out} $、測定される$ \ Delta A_ {in} $は呼び出されます。 sensitivity, S。数学的には、次のように表すことができます。

$$ S = \ frac {\ Delta A_ {out}} {\ Delta A_ {in}} $$

感度という用語は、測定器が応答するために必要な測定可能な入力の最小の変化を意味します。

• 検量線が linearの場合、機器の感度は一定になり、検量線の傾きに等しくなります。

• 検量線が non-linearの場合、機器の感度は一定ではなく、入力に対して変化します。

解決

入力の特定の増分がある場合にのみ計測器の出力が変化する場合、入力のその増分が呼び出されます Resolution。つまり、入力の分解能がある場合、機器は入力を効果的に測定することができます。

動的特性

時間に対して非常に急速に変化する量またはパラメータを測定するために使用される機器の特性は、動的特性と呼ばれます。以下はのリストですdynamic characteristics。

• 応答速度
• 動的エラー
• Fidelity
• Lag

それでは、これらの動的特性について1つずつ説明していきましょう。

応答速度

測定量に変化があった場合に計測器が応答する速度を speed of response。計測器の速度を示します。

遅れ

測定する量に変化があるときはいつでも、測定器の応答に存在する遅延の量は、測定ラグと呼ばれます。単に呼ばれることもありますlag。

動的エラー

時間に対して変化する量の真の値$ A_ {t} $と機器の指示値$ A_ {i} $の差は、動的エラー$ e_ {d} $として知られています。

忠実度

計測器が動的エラーなしに測定量の変化を示す程度は、 Fidelity

測定中に発生するエラーは、 measurement errors。この章では、測定誤差の種類について説明します。

測定誤差の種類

測定誤差は次の3種類に分類できます。

• グロスエラー
• ランダムエラー
• 体系的なエラー

ここで、これら3種類の測定誤差について1つずつ説明します。

グロスエラー

測定値を取得する際の観察者の経験不足が原因で発生するエラーは、次のように知られています。 gross errors。グロスエラーの値は、オブザーバーごとに異なります。場合によっては、機器の不適切な選択が原因で重大なエラーが発生することもあります。これらの2つの手順に従うことで、重大なエラーを最小限に抑えることができます。

• 測定する値の範囲に基づいて、最適な機器を選択してください。
• 読み取り値を注意深く書き留めます

体系的なエラー

機器がエラーを生成する場合、それはその操作中に一定の均一な偏差であり、として知られています systematic error。系統的なエラーは、機器で使用されている材料の特性が原因で発生します。

Types of Systematic Errors

系統的エラーは次のように分類できます three types。

• Instrumental Errors −このタイプのエラーは、機器の欠点と負荷の影響が原因で発生します。

• Environmental Errors −この種のエラーは、温度や圧力などの変化などの環境の変化によって発生します。

• observational Errors −このタイプのエラーは、メーターの読み取り中にオブザーバーが原因で発生します。 Parallax errors このタイプのエラーに属します。

ランダムエラー

測定時間中に原因不明で発生するエラーは、次のように知られています。 random errors。したがって、これらのエラーを排除または最小化することはできません。ただし、ランダムエラーなしでより正確な測定値を取得したい場合は、次の2つの手順に従うことで可能です。

• Step1 −さまざまなオブザーバーによるより多くの読み取り値を取得します。

• Step2 −ステップ1で得られた読み取り値の統計分析を行います。

以下は、統計分析で使用されるパラメーターです。

• Mean
• Median
• Variance
• Deviation
• 標準偏差

さて、これらについて話し合いましょう statistical parameters。

平均

$ x_ {1}、x_ {2}、x_ {3}、....、x_ {N} $を特定の測定値の$ N $の読み取り値とします。平均またはaverage value これらの読み取り値のうち、次の式を使用して計算できます。

$$ m = \ frac {x_ {1} + x_ {2} + x_ {3} + .... + x_ {N}} {N} $$

ここで、$ m $は平均値または平均値です。

特定の測定値の読み取り数が多い場合、平均値または平均値はほぼ次のようになります。 true value

中央値

特定の測定値の読み取り数が多い場合、平均値または平均値を計算することは困難です。ここで、median value そしてそれは平均値にほぼ等しくなります。

中央値を計算するには、最初に特定の測定値の読み取り値を ascending order。読み取り数が次の場合、次の式を使用して中央値を計算できます。odd number。

$$ M = x _ {\ left（\ frac {N + 1} {2} \ right）} $$

読み取り数が次の場合、次の式を使用して中央値を計算できます。 even number。

$$ M = \ frac {x _ {\ left（N / 2 \ right）} + x_ \ left（\ left [N / 2 \ right] +1 \ right）} {2} $$

平均からの逸脱

特定の測定値の読み取り値と平均値の差は、平均からの偏差として知られています。要するに、それは偏差と呼ばれます。数学的には、次のように表すことができます。

$$ d_ {i} = x_ {i} -m $$

どこ、

$ d_ {i} $は、$ i ^ {th} $の読み取り値の平均からの偏差です。

$ x_ {i} $は、$ i ^ {th} $の読み取り値です。

$ m $は平均値または平均値です。

標準偏差

偏差の二乗平均平方根はと呼ばれます standard deviation。数学的には、次のように表すことができます。

$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N}} $$

上記の式は、読み取り値の数Nが20以上の場合に有効です。読み取り値の数Nが20未満の場合、標準偏差には次の式を使用できます。

$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N-1}} $$

どこ、

$ \ sigma $は標準偏差です

$ d_ {1}、d_ {2}、d_ {3}、…、d_ {N} $は、それぞれ平均からの1番目、2番目、3番目、…、$ N ^ {th} $の読み取り値の偏差です。

Note −標準偏差の値が小さい場合、測定値の読み取り精度が高くなります。

分散

標準偏差の2乗はと呼ばれます variance。数学的には、次のように表すことができます。

$$ V = \ sigma ^ {2} $$

どこ、

$ V $は分散です

$ \ sigma $は標準偏差です

偏差の平均二乗は、 variance。数学的には、次のように表すことができます。

$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N} $$

上記の式は、読み取り値の数Nが20以上の場合に有効です。読み取り値の数Nが20未満の場合、分散には次の式を使用できます。

$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N-1} $$

どこ、

$ V $は分散です

$ d_ {1}、d_ {2}、d_ {3}、…、d_ {N} $は、それぞれ平均からの1番目、2番目、3番目、…、$ N ^ {th} $の読み取り値の偏差です。

したがって、統計パラメータの助けを借りて、特定の測定値の読み取り値を分析できます。このようにして、より正確な測定値を取得します。

任意の量を測定するために使用される機器は、 measuring instruments。機器が電圧や電流などの基本的な電気量を測定できる場合、basic measuring instruments。

基本的な測定器の種類

基本的な測定器は次の2種類に分類できます。

• Voltmeters
• Ammeters

これら2つの基本的な測定器について簡単に説明しましょう。

電圧計

名前が示すように、 voltmeter電気回路の任意の2点間の電圧を測定する測定器です。電圧の単位はボルトで、測定器はメートルです。したがって、「電圧計」という言葉は、2つの言葉を組み合わせることによって得られます“volt” そして “meter”。

電圧計は次のように分類できます。 two types 測定できる電圧の種類に基づいています。

• DC電圧計
• AC電圧計

DC電圧計

名前が示すように、DC電圧計は DC voltage電気回路の任意の2点にわたって。実用的なDC電圧計を下図に示します。

図に示されているDC電圧計は $(0-10)V$ DC voltmeter。したがって、0ボルトから10ボルトまでのDC電圧を測定するために使用できます。

AC電圧計

名前が示すように、AC電圧計は AC voltage電気回路の任意の2点にわたって。実用的なAC電圧計を下図に示します。

上図に示すAC電圧計は $(0-250)V$ AC voltmeter。したがって、0ボルトから250ボルトまでのAC電圧を測定するために使用できます。

電流計

名前が示すように、 ammeter電気回路の任意の2点を流れる電流を測定する測定器です。電流の単位はアンペアで、測定器はメートルです。「電流計」という言葉は、“am” アンペアの “meter”。

電流計は次のように分類できます。 two types 測定できる電流の種類に基づいています。

• DC電流計
• AC電流計

DC電流計

名前が示すように、DC電流計は DC currentそれは電気回路の任意の2点を通って流れます。実用的なDC電流計を図に示します。

上図に示すDC電流計は $(0-50)A$ DC ammeter。したがって、ゼロアンペアから50アンペアまでのDC電流を測定するために使用できます。

AC電流計

名前が示すように、AC電流計は AC currentそれは電気回路の任意の2点を通って流れます。実用的なAC電流計を下図に示します。

上図に示すAC電流計は $(0-100)A$ AC ammeter。したがって、ゼロアンペアから100アンペアまでのAC電流を測定するために使用できます。

次のいくつかの章で、さまざまな電圧計と電流計について詳しく説明します。

DC電圧計は、電気回路の任意の2点間のDC電圧を測定するために使用される測定器です。永久磁石ムービングコイル（PMMC）検流計と直列に抵抗を配置すると、組み合わせ全体が次のように機能します。DC voltmeter。

DC電圧計で使用される直列抵抗は、直列乗算器抵抗または単に乗算器とも呼ばれます。基本的に、検流計の電流がフルスケールのたわみ値を超えないようにするために、検流計を流れる電流の量を制限します。ザ・circuit diagram 直流電圧計の概要を下図に示します。

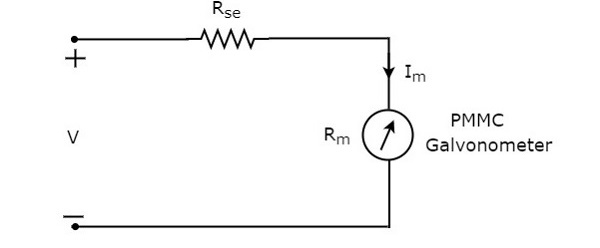
このDC電圧計は、DC電圧を測定する電気回路の2点に配置する必要があります。

適用する KVL 上記の回路のループの周り。

$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ （式1）

$$ \ Rightarrow V-I_ {m} R_ {m} = I_ {m} R_ {se} $$

$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$

$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}}-R_ {m} $ （式2）

どこ、

$ R_ {se} $は直列乗算器の抵抗です

$ V $は、測定される全範囲のDC電圧です。

$ I_ {m} $はフルスケールのたわみ電流です

$ R_ {m} $は検流計の内部抵抗です

測定されるフルレンジDC電圧の比率$ V $と、検流計の両端のDC電圧降下$ V_ {m} $は、次のように知られています。 multiplying factor、m。数学的には、次のように表すことができます。

$ m = \ frac {V} {V_ {m}} $ （式3）

式1から、次の式が得られます。 full range DC voltage それは測定される、$ V $です。

$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ （式4）

ザ・ DC voltage drop検流計全体で、$ V_ {m} $は、フルスケールのたわみ電流$ I_ {m} $と検流計の内部抵抗$ R_ {m} $の積です。数学的には、次のように書くことができます

$ V_ {m} = I_ {m} R_ {m} $ （式5）

Substitute、式4および式3の式5。

$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$

$ \ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1 $

$ \ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}} $

$ R_ {se} = R_ {m} \ left（m-1 \ right）$ （式6）

私たちは見つけることができます value of series multiplier resistance 利用可能なデータに基づいて、式2または式6のいずれかを使用します。

マルチレンジDC電圧計

前のセクションでは、PMMC検流計と直列に乗算器抵抗を配置することによって得られるDC電圧計について説明しました。このDC電圧計は、particular range DC電圧の。

のDC電圧を測定するためにDC電圧計を使用したい場合 multiple ranges、次に、単一の乗算器抵抗器の代わりに複数の並列乗算器抵抗器を使用する必要があり、この抵抗器の組み合わせ全体がPMMC検流計と直列になっています。ザ・circuit diagram マルチレンジDC電圧計の概要を下図に示します。

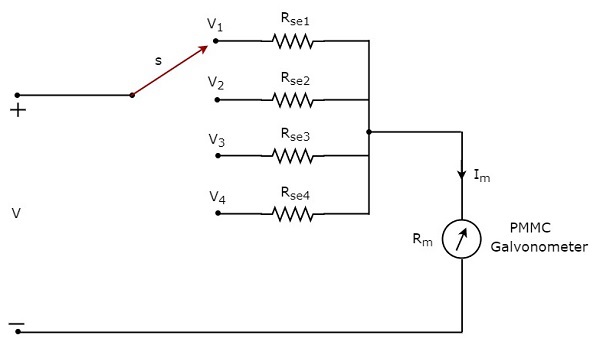
これを配置する必要があります multi range DC voltmeter必要な範囲のDC電圧を測定する電気回路の2点間。スイッチをそれぞれの乗算器抵抗に接続することにより、希望する電圧範囲を選択できます。

$ m_ {1}、m_ {2}、m_ {2} $、および$ m_ {4} $を multiplying factors全範囲のDC電圧がそれぞれ$ V_ {1}、V_ {2}、V_ {3} $、および$ V_ {4} $として測定されると考えると、DC電圧計の 以下は、各倍率に対応する式です。

$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$

$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$

$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$

$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$

上記の回路には4つあります series multiplier resistors、$ R_ {se1}、R_ {se2}、R_ {se3} $、および$ R_ {se4} $。これらの4つの抵抗に対応する式は次のとおりです。

$$ R_ {se1} = R_ {m} \ left（m_ {1} -1 \ right）$$

$$ R_ {se2} = R_ {m} \ left（m_ {2} -1 \ right）$$

$$ R_ {se3} = R_ {m} \ left（m_ {3} -1 \ right）$$

$$ R_ {se4} = R_ {m} \ left（m_ {4} -1 \ right）$$

したがって、上記の式を使用して、各直列乗算器抵抗器の抵抗値を見つけることができます。

電気回路の任意の2点間のAC電圧を測定するために使用される機器は、 AC voltmeter。AC電圧計が整流器で構成されている場合、それは整流器ベースのAC電圧計であると言われます。

DC電圧計はDC電圧のみを測定します。AC電圧の測定に使用する場合は、次の2つの手順を実行する必要があります。

• Step1 −整流器を使用して、AC電圧信号をDC電圧信号に変換します。

• Step2 −整流器の出力信号のDCまたは平均値を測定します。

我々が得る Rectifier based AC voltmeter、基本的なDC電圧計に整流回路を含めるだけです。この章では、整流器ベースのAC電圧計について説明します。

整流器ベースのAC電圧計の種類

以下は two types 整流器ベースのAC電圧計の。

• 半波整流器を使用したAC電圧計
• 全波整流器を使用したAC電圧計

それでは、これら2つのAC電圧計について1つずつ説明しましょう。

半波整流器を使用したAC電圧計

半波整流器がDC電圧計の前に接続されている場合、その組み合わせ全体は、半波整流器を使用するAC電圧計と呼ばれます。ザ・block diagram 半波整流器を使用したAC電圧計の動作を下図に示します。

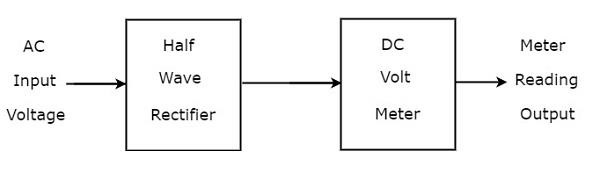
上記のブロック図は、半波整流器とDC電圧計の2つのブロックで構成されています。上記のブロック図の各ブロックをそれぞれのコンポーネントに置き換えるだけで、対応する回路図が得られます。だから、circuit diagram 半波整流器を使用したAC電圧計の動作は下図のようになります。

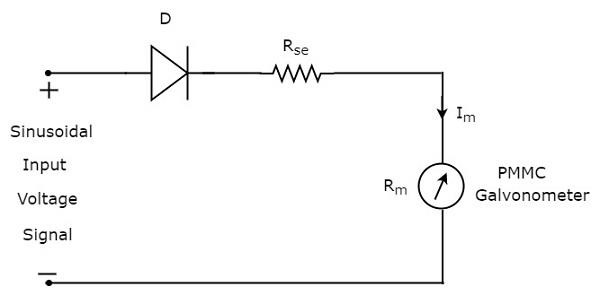
ザ・ rms value 正弦波（AC）入力電圧信号の

$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$

$$ \ Rightarrow V_ {m} = \ sqrt {2} V_ {rms} $$

$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$

どこ、

$ V_ {m} $は、正弦波（AC）入力電圧信号の最大値です。

ザ・ DC または半波整流器の出力信号の平均値は

$$ V_ {dc} = \ frac {V_ {m}} {\ pi} $$

Substitute、上記の式の$ V_ {m} $の値。

$$ V_ {dc} = \ frac {1.414 V_ {rms}} {\ pi} $$

$$ V_ {dc} = 0.45 V_ {rms} $$

したがって、AC電圧計は、次の値に等しい出力電圧を生成します。 0.45 正弦波（AC）入力電圧信号のrms値の倍

全波整流器を使用したAC電圧計

全波整流器がDC電圧計の前に接続されている場合、その組み合わせ全体は、全波整流器を使用するAC電圧計と呼ばれます。ザ・block diagram 全波整流器を使用したAC電圧計の概要を下図に示します。

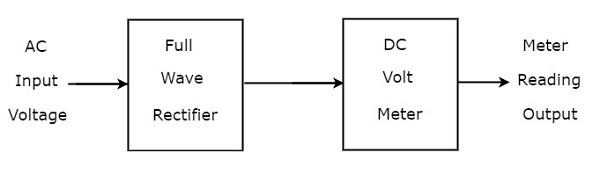
上記のブロック図は、全波整流器とDC電圧計の2つのブロックで構成されています。上記のブロック図の各ブロックをそれぞれのコンポーネントに置き換えるだけで、対応する回路図が得られます。

だから、 circuit diagram 全波整流器を使用したAC電圧計の動作は下図のようになります。

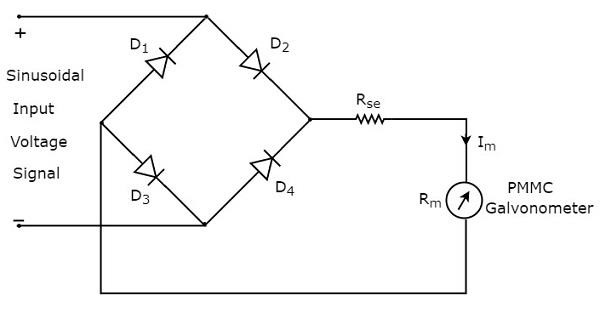
ザ・ rms value 正弦波（AC）入力電圧信号の

$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$

$$ \ Rightarrow V_ {m} = \ sqrt {2} \：V_ {rms} $$

$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$

どこ、

$ V_ {m} $は、正弦波（AC）入力電圧信号の最大値です。

ザ・ DC または全波整流器の出力信号の平均値は

$$ V_ {dc} = \ frac {2V_ {m}} {\ pi} $$

Substitute、上記の式の$ V_ {m} $の値

$$ V_ {dc} = \ frac {2 \ times 1.414 \：V_ {rms}} {\ pi} $$

$$ V_ {dc} = 0.9 \：V_ {rms} $$

したがって、AC電圧計は、次の値に等しい出力電圧を生成します。 0.9 正弦波（AC）入力電圧信号のrms値の倍。

前の章では、整流器ベースのAC電圧計について説明しました。この章では、次の2種類のAC電圧計について説明します。

• ピーク応答AC電圧計
• 真のRMS応答AC電圧計

それでは、この2種類のAC電圧計について1つずつ説明しましょう。

ピーク応答AC電圧計

名前が示すように、ピーク応答AC電圧計はに応答します peak valuesAC電圧信号の。つまり、この電圧計はAC電圧のピーク値を測定します。ザ・circuit diagram ピーク応答AC電圧計の以下を示します-

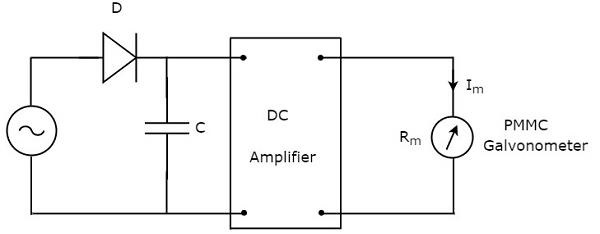
上記の回路は、ダイオード、コンデンサ、DCアンプ、PMMC検流計で構成されています。上記の回路にあるダイオードは、整流の目的で使用されます。そのため、ダイオードはAC電圧信号をDC電圧信号に変換します。コンデンサは、このDC電圧信号のピーク値まで充電されます。

中 positive half cycleAC電圧信号の場合、ダイオードが導通し、コンデンサがAC電圧信号のピーク値まで充電されます。AC電圧信号の値がこの値よりも小さい場合、ダイオードは逆バイアスされます。

したがって、コンデンサは、AC電圧信号の次の正の半サイクルまでDCアンプの抵抗を介して放電します。AC電圧信号の値がコンデンサ電圧よりも大きい場合、ダイオードが導通し、プロセスが繰り返されます。

コンデンサの充電が速く、放電が遅いように成分値を選択する必要があります。その結果、メーターは常にこのコンデンサー電圧に応答します。peak value of AC voltage。

真のRMS応答AC電圧計

名前が示すように、真のRMS応答AC電圧計は、AC電圧信号の真のRMS値に応答します。この電圧計は、AC電圧のRMS値を測定します。ザ・circuit diagram 真のRMS応答AC電圧計の例を下の図に示します。

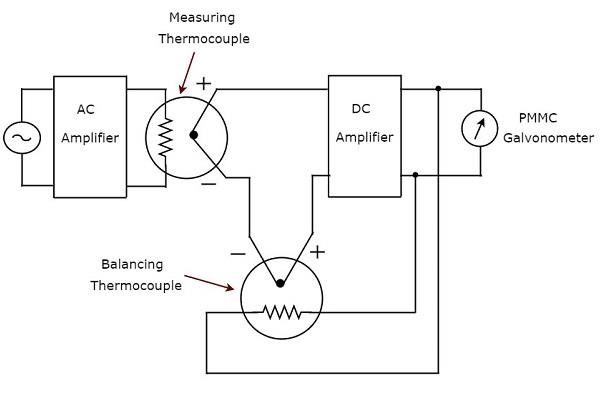
上記の回路は、AC増幅器、2つの熱電対、DC増幅器、およびPMMC検流計で構成されています。ACアンプはAC電圧信号を増幅します。上記の回路で使用されている2つの熱電対は、測定熱電対と平衡熱電対です。Measuring thermocouple AC電圧信号のRMS値に比例する出力電圧を生成します。

熱電対は、入力量の2乗を通常の量に変換します。これは、熱電対の出力と入力の間に非線形の関係が存在することを意味します。フィードバック回路で別の熱電対を使用することにより、熱電対の非線形動作の影響を無視できます。上記の回路でこの目的に使用される熱電対は、balancing thermocouple。

2つの熱電対、つまり測定熱電対と平衡熱電対は、DCアンプの入力で花嫁を形成します。その結果、メーターは常に応答しますtrue RMS value AC電圧信号の。

電流は電荷の流量です。この電荷が一方向にのみ流れる場合、結果として生じる電流は直流（DC）と呼ばれます。と呼ばれる直流を測定するために使用される機器DC ammeter。

永久磁石ムービングコイル（PMMC）検流計と並列に抵抗を配置すると、組み合わせ全体がDC電流計として機能します。DC電流計で使用される並列抵抗は、シャント抵抗または単にshunt。大きな値のDC電流を測定するには、この抵抗の値を小さくする必要があります。

ザ・ circuit diagram DC電流計の概要を下図に示します。

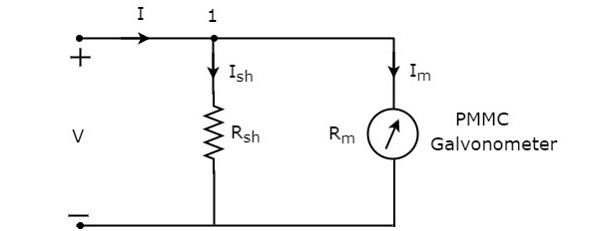
これを配置する必要があります DC ammeterDC電流が測定される電気回路の分岐と直列に接続されています。並列に接続されている要素間の電圧は同じです。したがって、シャント抵抗の両端の電圧$ R_ {sh} $と検流計の抵抗の両端の電圧$ R_ {m} $は同じです。これは、これら2つの要素が上記の回路で並列に接続されているためです。Mathematically、次のように書くことができます

$$ I_ {sh} R_ {sh} = I_ {m} R_ {m} $$

$ \ Rightarrow R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}} $ （式1）

ザ・ KCL equation ノード1には

$$-I + I_ {sh} + I_ {m} = 0 $$

$$ \ Rightarrow I_ {sh} = I-I_ {m} $$

Substitute 式1の$ I_ {sh} $の値。

$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}} $ （式2）

式2の右辺にある分母の項で一般的な$ I_ {m} $を考えてみましょう。

$$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {m}（\ frac {1} {I_ {m}}-1）} $$

$ \ Rightarrow R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}}-1} $ （式3）

どこ、

$ R_ {sh} $はシャント抵抗です

$ R_ {m} $は検流計の内部抵抗です

$ I $は、測定される直流電流の合計です。

$ I_ {m} $はフルスケールのたわみ電流です

測定される総直流電流$ I $と検流計のフルスケールたわみ電流$ I_ {m} $の比率は次のように知られています。 multiplying factor, m。数学的には、次のように表すことができます。

$ m = \ frac {I} {I_ {m}} $ （式4）

$ R_ {sh} = \ frac {R_ {m}} {m-1} $ （式5）

私たちは見つけることができます value of shunt resistance 利用可能なデータに基づいて、式2または式5のいずれかを使用します。

マルチレンジDC電流計

前のセクションでは、PMMC検流計と並列に抵抗を配置することによって得られるDC電流計について説明しました。このDC電流計は、particular range 直流の。

の直流電流を測定するためにDC電流計を使用したい場合 multiple ranges、次に、単一の抵抗器の代わりに複数の並列抵抗器を使用する必要があり、この抵抗器の組み合わせ全体がPMMC検流計と並列になります。ザ・circuit diagram マルチレンジDC電流計の概要を下図に示します。

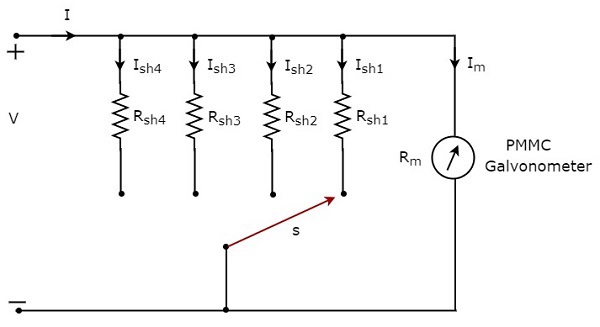
このマルチレンジDC電流計を、必要な範囲の直流を測定する電気回路の分岐と直列に配置します。必要な電流範囲は、スイッチsをそれぞれのシャント抵抗に接続することによって選択されます。

$ m_ {1}、m_ {2}、m_ {3} $、$ m_ {4} $を multiplying factors合計直流電流をそれぞれ$ I_ {1}、I_ {2}、I_ {3} $、および$ I_ {4} $として測定すると見なした場合のDC電流計の値。以下は、各倍率に対応する式です。

$$ m_ {1} = \ frac {I_ {1}} {I_ {m}} $$

$$ m_ {2} = \ frac {I_ {2}} {I_ {m}} $$

$$ m_ {3} = \ frac {I_ {3}} {I_ {m}} $$

$$ m_ {4} = \ frac {I_ {4}} {I_ {m}} $$

上記の回路には4つあります shunt resistors、$ R_ {sh1}、R_ {sh2}、R_ {sh2} $、および$ R_ {sh4} $。これらの4つの抵抗に対応する式は次のとおりです。

$$ R_ {sh1} = \ frac {R_ {m}} {m_ {1} -1} $$

$$ R_ {sh2} = \ frac {R_ {m}} {m_ {2} -1} $$

$$ R_ {sh3} = \ frac {R_ {m}} {m_ {3} -1} $$

$$ R_ {sh4} = \ frac {R_ {m}} {m_ {4} -1} $$

上記の式は、各シャント抵抗の抵抗値を見つけるのに役立ちます。

電流は電荷の流量です。この電荷の方向が定期的に変化する場合、結果として生じる電流はAlternating Current (AC)。

電気回路の任意の分岐を流れる交流電流を測定するために使用される機器は、 AC ammeter。

Example −熱電対型交流電流計。

それでは、熱電対型交流電流計についてお話ししましょう。

熱電対タイプAC電流計

熱電対がPMMC検流計の前に接続されている場合、その組み合わせ全体が熱電対タイプのAC電流計と呼ばれます。ザ・block diagram 熱電対型交流電流計の概要を下図に示します。

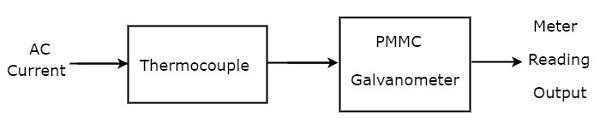
上記のブロック図は、主に熱電対とPMMC検流計の2つのブロックで構成されています。上記のブロック図の各ブロックをそれぞれのコンポーネントに置き換えるだけで、対応する回路図が得られます。だから、circuit diagram 熱電対型交流電流計は下図のようになります。

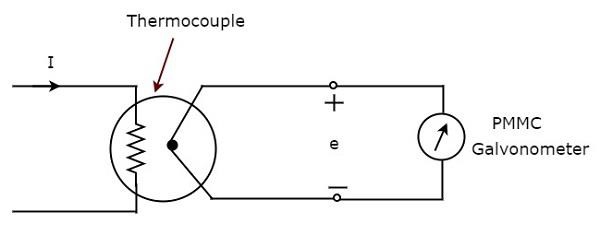
熱電対は、交流電流Iがヒーターエレメントを流れるたびにEMF $ e $を生成します。このEMF、$ e $は、ヒーターエレメントを流れる電流Iのrms値に正比例します。したがって、PMMC機器のスケールを校正して読み取る必要がありますrms values of current。

したがって、この章では、DC電圧計、AC電圧計、DC電流計、AC電流計などのすべての基本的な測定器を完成させました。次の章では、抵抗値を測定するメーターや測定器について説明します。

電気回路の任意の2点間の抵抗値を測定するために使用される機器は、 ohmmeter。また、未知の抵抗の値を見つけるために使用することもできます。抵抗の単位はオームで、測定器はメートルです。したがって、「オーム計」という言葉は、これらの言葉を組み合わせることによって得られます“ohm” そして “meter”。

抵抗計の種類

以下は two types 抵抗計の。

• シリーズ抵抗計
• シャント抵抗計

それでは、これら2種類の抵抗計について1つずつ説明しましょう。

シリーズ抵抗計

抵抗器の値が不明で、抵抗計と直列に配置して測定する必要がある場合、その抵抗計は直列抵抗計と呼ばれます。ザ・circuit diagram 直列抵抗計の概要を下図に示します。

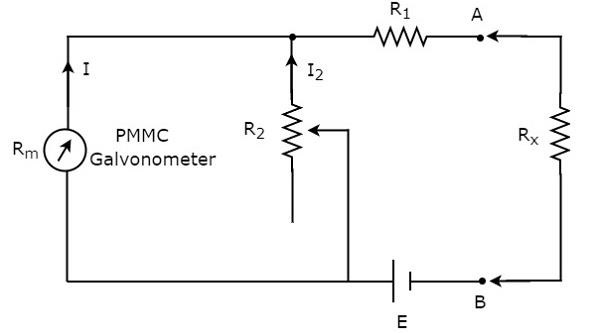
端子AとBの左側にある回路の部分は series ohmmeter。したがって、端子AとBの右側に配置することで、未知の抵抗の値を測定できます。次に、calibration scale シリーズオーム計の。

• $ R_ {x} = 0 \：\ Omega $の場合、端子AとBは互いに短絡します。したがって、メーター電流は抵抗$ R_ {1} $と$ R_ {2} $の間で分割されます。ここで、メーター電流全体が抵抗器$ R_ {1} $のみを流れるように、抵抗器$ R_ {2} $の値を変更します。この場合、メーターは満杯になりますscale deflection current。したがって、メーターのこのフルスケールのたわみ電流は、$ 0 \：\ Omega $として表すことができます。

• $ R_ {x} = \ infty \：\ Omega $の場合、端子AとBは互いに開回路になります。したがって、抵抗$ R_ {1} $には電流が流れません。この場合、メーターはヌル偏向電流を示します。したがって、メーターのこのヌルたわみは、$ \ infty \ Omega $として表すことができます。

• このように、$ R_ {x} $のさまざまな値を考慮することにより、メーターはさまざまなたわみを示します。したがって、これらのたわみを対応する抵抗値で表すことができます。

直列抵抗計は、校正スケールで構成されています。スケールの右手と左手の終点にそれぞれ0 $ \ Omega $と$ \ infty \：\ Omega $の表示があります。直列抵抗計は測定に役立ちますhigh values of resistances.

シャント抵抗計

抵抗の値が不明で、抵抗計と並列（シャント）に配置して測定する場合、その抵抗計はシャント抵抗計と呼ばれます。ザ・circuit diagram シャントオーム計の概要を下図に示します。

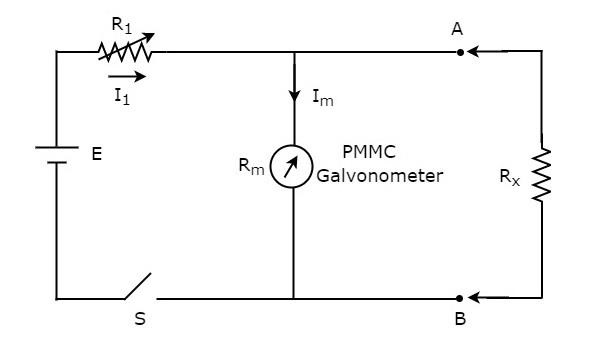
端子AとBの左側にある回路の部分は shunt ohmmeter。したがって、端子AとBの右側に配置することで、未知の抵抗の値を測定できます。

それでは、 calibration scaleシャント抵抗計の。使用中は上記回路のスイッチSを閉じてください。

• $ R_ {x} = 0 \：\ Omega $の場合、端子AとBは互いに短絡します。このため、電流$ I_ {1} $全体が端子AとBを流れます。この場合、PMMC検流計には電流が流れません。従ってnull deflection PMMC検流計のは$ 0 \：\ Omega $として表すことができます。

• $ R_ {x} = \ infty \：\ Omega $の場合、端子AとBは互いに開回路になります。したがって、端子AとBには電流が流れません。この場合、電流全体$ I_ {1} $がPMMC検流計に流れます。必要に応じて、PMMC検流計がフルスケールのたわみ電流を示すまで、抵抗の値$ R_ {1} $を変更（調整）します。したがって、これはfull scale deflection PMMC検流計の電流は$ \ infty \：\ Omega $として表すことができます

• このように、$ R_ {x} $のさまざまな値を考慮することにより、メーターはさまざまなたわみを示します。したがって、それに応じて、これらのたわみを対応する抵抗値で表すことができます。

シャント抵抗計は、校正スケールで構成されています。目盛りの左手と右手の終点にそれぞれ$ 0 \：\ Omega $と$ \ infty \：\ Omega $の表示があります。

シャント抵抗計は測定に役立ちます low values of resistances。したがって、測定する抵抗の値、つまり高または低に基づいて、直列抵抗計またはシャント抵抗計のいずれかを使用できます。

前の章では、電圧計、電流計、抵抗計について説明しました。これらの測定器は、それぞれ電圧、電流、抵抗を測定するために使用されます。つまり、separate measuring instruments 電圧、電流、抵抗を測定します。

単一の測定器を使用して、電圧、電流、抵抗などの量を一度に1つずつ測定できるとすると、次のようになります。 multimeter。一度に複数の電気量を測定できるため、マルチメータという名前が付けられています。

マルチメータを使用した測定

Multimeterは、いくつかの範囲のDCおよびAC電圧、DCおよびAC電流、および抵抗を測定するために使用される機器です。電子マルチメータまたは電圧オームメータ（VOM）とも呼ばれます。

DC電圧測定

の一部 circuit diagram 直流電圧の測定に使用できるマルチメータの概要を下図に示します。

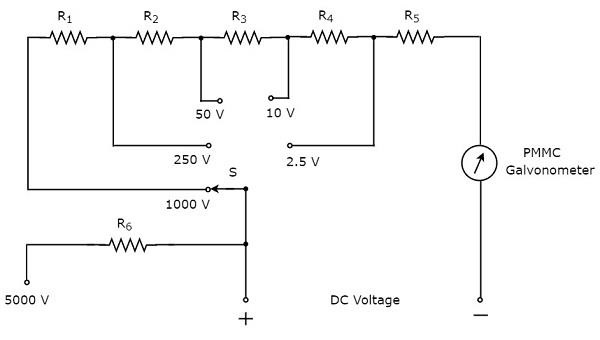
上記の回路は、マルチレンジDC電圧計のように見えます。PMMC検流計と直列の抵抗器の組み合わせはDC voltmeter。したがって、特定の値までのDC電圧を測定するために使用できます。

抵抗値を大きくすることで、同じ直流電圧計で測定できる直流電圧の範囲を広げることができます。抵抗器を接続すると、等価抵抗値が増加します。series。

上記の回路では、最大DC電圧を測定できます。 2.5V抵抗器、$ R_ {5} $をPMMC検流計と直列に組み合わせて使用​​します。前の回路と直列に抵抗$ R_ {4} $を接続することにより、最大DC電圧を測定できます。10V。このように、前の（以前の）回路と直列に抵抗を接続するだけで、DC電圧の範囲を広げることができます。

スイッチSを希望の電圧範囲に接続することにより、電気回路の任意の2点間のDC電圧を測定できます。

DC電流測定

の一部 circuit diagram 直流電流の測定に使用できるマルチメータの概要を下図に示します。

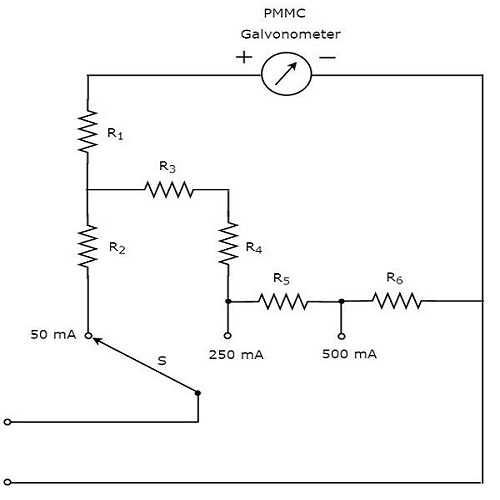
上記の回路は、マルチレンジDC電流計のように見えます。PMMC検流計と並列の抵抗の組み合わせはDC ammeter。そのため、特定の値までのDC電流を測定するために使用できます。

私たちは手に入れる different ranges前の抵抗器と並列に抵抗器を配置することにより、同じDC電流計で測定されたDC電流の。上記の回路では、大電流によるメーターの損傷を防ぐために、抵抗$ R_ {1} $がPMMC検流計と直列に接続されています。

スイッチSを希望の電流範囲に接続することにより、電気回路の任意の2点を流れるDC電流を測定できます。

AC電圧測定

の一部 circuit diagram AC電圧の測定に使用できるマルチメータの概要を下図に示します。

上記の回路は次のようになります multi range AC voltmeter。整流器をDC電圧計と直列（カスケード）に配置するだけでAC電圧計が得られることはわかっています。上記の回路は、ダイオードの組み合わせと抵抗、$ R_ {6} $を抵抗、$ R_ {5} $とPMMC検流計の間に配置するだけで作成されました。

スイッチSを希望の電圧範囲に接続することにより、電気回路の任意の2点間のAC電圧を測定できます。

抵抗測定

の一部 circuit diagram 抵抗の測定に使用できるマルチメータの概要を下図に示します。

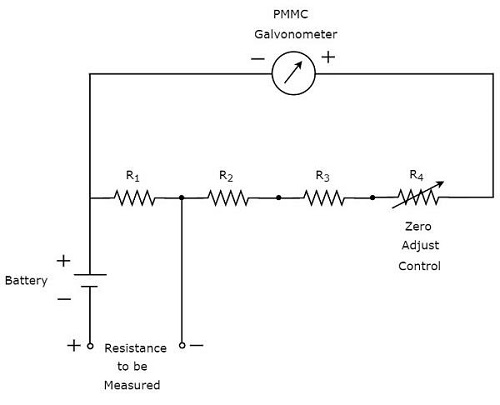
測定を行う前に、次の2つのタスクを実行する必要があります。

• 機器を短絡する
• メーターがフルスケール電流を示すまで、ゼロ調整コントロールを変更します。つまり、メーターはゼロ抵抗値を示します。

ここで、上記の回路はシャントオーム計として動作し、1のスケール乗算、つまり100を持ち^ます。高抵抗を測定するためのスケール乗算として、10の高次の累乗を考慮することもできます。

Signal generator は、正弦波、方形波、三角波などの標準的なテスト信号を提供する電子機器です。周期的な信号を生成するため、発振器とも呼ばれます。

可聴周波数（AF）範囲の周波数を持つ周期信号を生成する信号発生器は、 AF signal generator。可聴周波数の範囲は20Hzから20KHzです。

AF正弦波および方形波発生器

要件に基づいて可聴周波数の範囲で正弦波または方形波のいずれかを生成するAF信号発生器は、AF正弦波および方形波発生器と呼ばれます。そのblock diagram下図に示します。

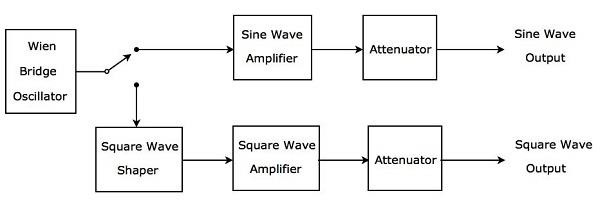
上記のブロック図は主に two paths。それらは上のパスと下のパスです。上のパスはAF正弦波を生成するために使用され、下のパスはAF方形波を生成するために使用されます。

Wien bridge oscillator可聴周波数の範囲で正弦波を生成します。要件に基づいて、ウィーンブリッジ発振器の出力をスイッチで上位パスまたは下位パスに接続できます。

上のパスは、正弦波増幅器や減衰器などのブロックで構成されています。スイッチを使用してウィーンブリッジ発振器の出力を上位パスに接続すると、目的のパスが生成されます。AF sine wave 上のパスの出力で。

下のパスは、方形波シェーパー、方形波増幅器、および減衰器のブロックで構成されています。方形波シェーパーは、正弦波を方形波に変換します。スイッチを使用してウィーンブリッジ発振器の出力をより低いパスに接続すると、目的のパスが生成されますAF square wave下のパスの出力で。このように、検討したブロック図を使用して、要件に基づいてAF正弦波またはAF方形波を生成できます。

関数発生器

関数発生器は、3つ以上の周期波を生成する信号発生器です。次のことを考慮してくださいblock diagram 三角波、方形波、正弦波などの周期波を生成する関数発生器の

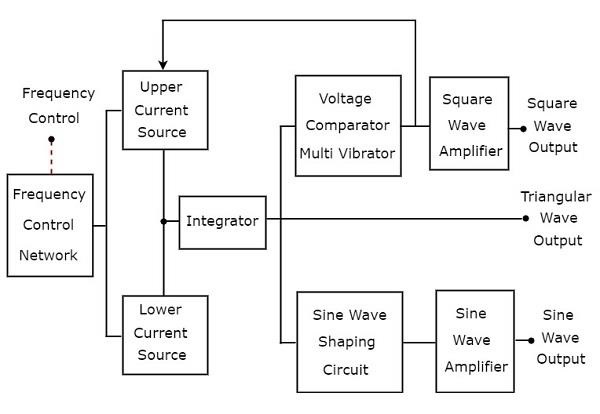
二つあります current sourcesつまり、上のブロック図の上部電流源と下部電流源です。これらの2つの電流源は、周波数制御された電圧によって調整されます。

三角波

Integrator上のブロック図にあるように、同じ時間、繰り返し、上部と下部の電流源から交互に定電流を取得します。したがって、積分器は2つのタイプの出力を同時に繰り返し生成します-

• 積分器の出力電圧 increases linearly 積分器が上部電流源から電流を得る期間の時間に関して。

• 積分器の出力電圧 decreases linearly 積分器がより低い電流源から電流を得る期間の時間に関して。

このようにして、上記のブロック図にある積分器は、 triangular wave。

方形波と正弦波

積分器の出力、つまり三角波は、それぞれ方形波と正弦波を取得するために、上のブロック図に示すように、他の2つのブロックへの入力として適用されます。これら2つについて1つずつ説明しましょう。

方形波

三角波は、正の傾きと負の傾きが交互に同じ時間繰り返されます。だから、voltage comparator multi vibrator 上記のブロック図にあるものは、次の2種類の出力を同じ時間繰り返し生成します。

• 定数の1つのタイプ (higher) voltage 電圧コンパレータマルチバイブレータが三角波の正の傾きを得る期間の電圧コンパレータマルチバイブレータの出力で。

• 別のタイプの定数 (lower) voltage 電圧コンパレータマルチバイブレータが三角波の負の傾きを得る期間の電圧コンパレータマルチバイブレータの出力で。

上記のブロック図にある電圧コンパレータマルチバイブレータは、 square wave。電圧コンパレータマルチバイブレータの出力で生成される方形波の振幅が十分でない場合は、方形波増幅器を使用して必要な値に増幅できます。

正弦波

ザ・ sine wave shaping circuit三角入力波から正弦波出力を生成します。基本的に、この回路はダイオード抵抗ネットワークで構成されています。正弦波整形回路の出力で生成される正弦波の振幅が不十分な場合は、正弦波増幅器を使用して必要な値に増幅することができます。

波を分析するために使用される電子機器は、 wave analyzer。信号と波という用語は頻繁に交換可能に使用できるため、信号アナライザとも呼ばれます。

私たちは表現することができます periodic signal 次の2つの項の合計として。

• DCコンポーネント
• 一連の正弦波高調波

したがって、周期信号の分析は、その中に存在する高調波成分の分析です。

基本的なウェーブアナライザー

基本的な波動アナライザーは、主に3つのブロック（一次検出器、全波整流器、PMMC検流計）で構成されています。ザ・block diagram 基本波アナライザーの概要を下図に示します。

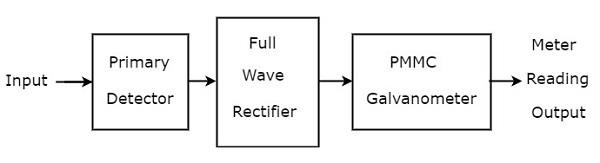
ザ・ function 基本波アナライザーに存在する各ブロックの概要を以下に示します。

• Primary Detector−LC回路で構成されています。インダクターLとコンデンサーCの値は、測定する必要のある高調波周波数成分のみが許容されるように調整できます。

• Full Wave Rectifier −AC入力をDC出力に変換します。

• PMMC Galvanometer −全波整流器の出力で得られる信号のピーク値を示します。

上記の基本波アナライザのブロック図の各ブロックをそれぞれのコンポーネントに置き換えるだけで、対応する回路図が得られます。だから、circuit diagram 基本波アナライザの図は次の図のようになります-

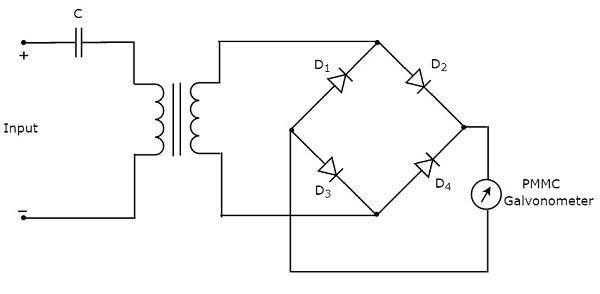
この基本波アナライザは、周期信号のすべての高調波周波数成分を分析するために使用できます。

ウェーブアナライザーの種類

ウェーブアナライザは次のように分類できます。 two types。

• 周波数選択波アナライザー
• スーパーヘテロダイン波アナライザー

それでは、これら2つのウェーブアナライザについて1つずつ説明しましょう。

周波数選択波アナライザー

AF範囲の信号を分析するために使用される波アナライザは、周波数選択波アナライザと呼ばれます。ザ・block diagram 周波数選択波アナライザーの概要を下図に示します。

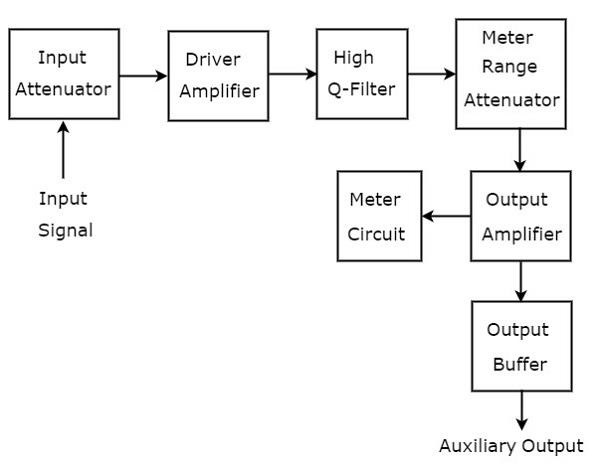
周波数選択波アナライザは、ブロックのセットで構成されています。ザ・function 各ブロックの以下に記載されています。

• Input Attenuator−解析対象のAF信号を入力アッテネータに印加します。信号の振幅が大きすぎる場合は、入力減衰器によって減衰させることができます。

• Driver Amplifier −必要に応じて受信信号を増幅します。

• High Q-filter−必要な周波数を選択し、不要な周波数を拒否するために使用されます。2つのRCセクションと2つのフィルターアンプで構成されており、これらはすべて互いにカスケード接続されています。10の累乗で周波数範囲を変更するために、静電容量値を変更できます。同様に、選択した範囲内で周波数を変更するために抵抗値を変更できます。

• Meter Range Attenuator −選択したAF信号を入力として取得し、必要に応じて減衰出力を生成します。

• Output Amplifier −必要に応じて、選択したAF信号を増幅します。

• Output Buffer −選択したAF信号を出力デバイスに提供するために使用されます。

• Meter Circuit−選択したAF信号の読みを表示します。メーターの読みは、ボルト範囲またはデシベル範囲で選択できます。

スーパーヘテロダイン波アナライザー

RF範囲の信号を分析するために使用される波アナライザーは、スーパーヘテロダイン波アナライザーと呼ばれます。次の図は、block diagram スーパーヘテロダイン波アナライザーの。

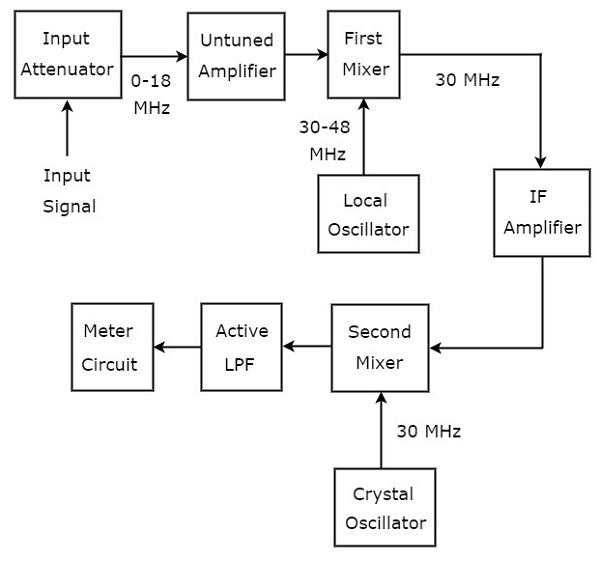
ザ・ working スーパーヘテロダイン波アナライザーの概要は以下のとおりです。

• 分析されるRF信号は、入力減衰器に適用されます。信号の振幅が大きすぎる場合は、次のように減衰させることができます。input attenuator。

• Untuned amplifier 必要に応じてRF信号を増幅し、最初のミキサーに適用します。

• 局部発振器のRF信号と出力の周波数範囲は、それぞれ0〜18 MHzと30〜48MHzです。そう、first mixer30MHzの周波数を持つ出力を生成します。これは、それに適用される2つの信号の周波数の差です。

• IF amplifier中間周波数（IF）信号、つまり最初のミキサーの出力を増幅します。増幅されたIF信号は2番目のミキサーに適用されます。

• 増幅されたIF信号と水晶発振器の出力の周波数は同じで30MHzに等しい。だから、second mixer周波数が0Hzの出力を生成します。これは、それに適用される2つの信号の周波数の差です。

• のカットオフ周波数 Active Low Pass Filter (LPF)1500Hzとして選択されます。したがって、このフィルターは2番目のミキサーの出力信号を許可します。

• Meter CircuitRF信号の読み取り値を表示します。メーターの読みは、ボルト範囲またはデシベル範囲で選択できます。

したがって、分析する信号の周波数範囲に基づいて、特定のウェーブアナライザを選択できます。

周波数領域で波を解析するために使用される電子機器は、 spectrum analyzer。基本的には、信号のエネルギー分布をCRT画面に表示します。ここで、x軸は周波数を表し、y軸は振幅を表します。

スペクトラムアナライザの種類

スペクトラムアナライザは次のように分類できます。 two types。

• フィルタバンクスペクトラムアナライザ
• スーパーヘテロダインスペクトラムアナライザ

ここで、これら2つのスペクトラムアナライザについて1つずつ説明します。

フィルタバンクスペクトラムアナライザ

AF範囲の信号を分析するために使用されるスペクトラムアナライザは、フィルタバンクスペクトラムアナライザと呼ばれます。 real time spectrum analyzer すべての入力周波数の変動を表示（表示）するためです。

次の図は、 block diagram フィルタバンクスペクトラムアナライザの。

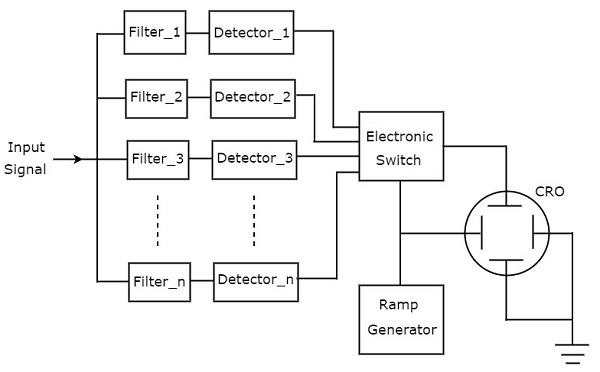
ザ・ working フィルタバンクスペクトラムアナライザの概要は以下のとおりです。

• バンドパスフィルターのセットがあり、それぞれが特定の周波数帯域を許可するように設計されています。各バンドパスフィルターの出力は、対応する検出器に渡されます。

• すべての検出器出力は電子スイッチに接続されています。このスイッチにより、検出器はCROの垂直偏向板に順次出力できます。したがって、CROは頻度を表示しますspectrum of AF signal そのCRT画面で。

スーパーヘテロダインスペクトラムアナライザ

RF範囲の信号を分析するために使用されるスペクトラムアナライザは、 superheterodyne spectrum analyzer。そのblock diagram 下図に示します。

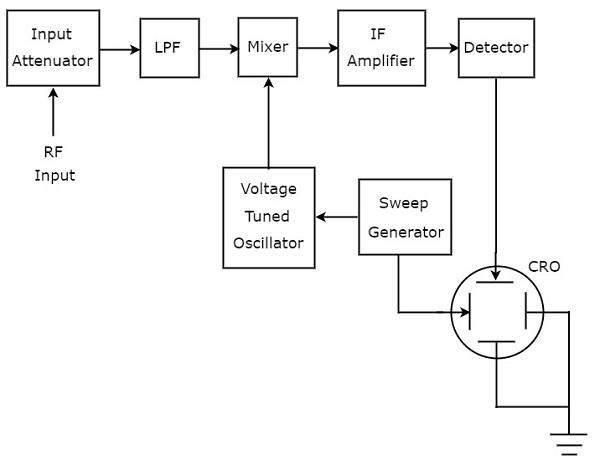
ザ・ working スーパーヘテロダインスペクトラムアナライザの概要は以下のとおりです。

• 分析されるRF信号は、入力減衰器に適用されます。信号の振幅が大きすぎる場合は、次のように減衰させることができます。input attenuator。

• Low Pass Filter （LPF）は、カットオフ周波数よりも低い周波数成分のみを許可します。

• Mixerローパスフィルターと電圧調整発振器から入力を取得します。それはそれに適用される2つの信号の周波数の差である出力を生成します。

• IF amplifier中間周波数（IF）信号、つまりミキサーの出力を増幅します。増幅されたIF信号は検出器に適用されます。

検出器の出力は、CROの垂直偏向板に与えられます。したがって、CROは頻度を表示しますspectrum of RF signal そのCRT画面で。

したがって、分析する信号の周波数範囲に基づいて、特定のスペクトラムアナライザを選択できます。

Oscilloscopeは、電圧波形を表示する電子機器です。オシロスコープの中で、ブラウン管オシロスコープ（CRO）が基本的なものであり、時間変化する信号または波形を表示します。

この章では、CROのブロック図とCROを使用したいくつかのパラメータの測定について説明します。

CROのブロック図

ブラウン管オシロスコープ（CRO）は、一連のブロックで構成されています。それらは、垂直増幅器、遅延線、トリガー回路、タイムベースジェネレーター、水平増幅器、ブラウン管（CRT）、および電源です。ザ・block diagram CROの概要を下図に示します。

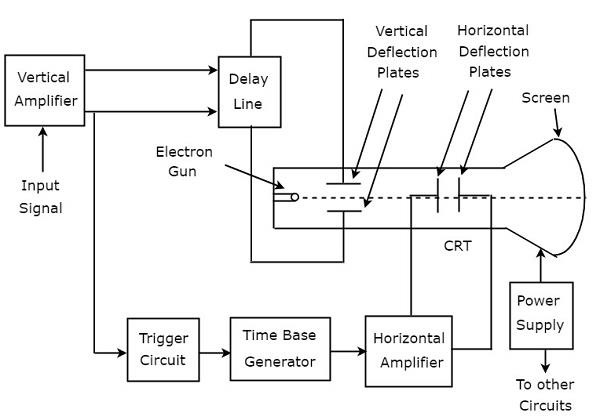
ザ・ function CROの各ブロックの概要は以下のとおりです。

• Vertical Amplifier −CRTの画面に表示される入力信号を増幅します。

• Delay Line−垂直増幅器の出力で得られる信号にある程度の遅延を提供します。この遅延信号は、CRTの垂直偏向板に適用されます。

• Trigger Circuit −電子ビームの水平偏向と垂直偏向の両方を同期させるためにトリガー信号を生成します。

• Time base Generator −電子ビームの水平偏向に役立つ鋸歯状信号を生成します。

• Horizontal Amplifier −のこぎり波信号を増幅し、CRTの水平偏向板に接続します。

• Power supply−高電圧と低電圧の両方を生成します。負の高電圧と正の低電圧は、それぞれCRTと他の回路に印加されます。

• Cathode Ray Tube (CRT)−これはCROの主要な重要なブロックであり、主に4つの部分で構成されています。それらは、電子銃、垂直偏向板、水平偏向板、および蛍光スクリーンです。

電子銃によって生成された電子ビームは、一対の垂直偏向板および一対の水平偏向板によってそれぞれ垂直方向および水平方向の両方に偏向される。最後に、偏向されたビームは蛍光スクリーン上にスポットとして表示されます。

このようにして、CROは適用された入力信号をCRTの画面に表示します。したがって、CROを使用して時間領域で信号を分析できます

CROを使用した測定

CROを使用して以下の測定を行うことができます。

• 振幅の測定
• 期間の測定
• 周波数の測定

それでは、これらの測定について1つずつ説明しましょう。

振幅の測定

CROは、電圧信号を時間の関数として画面に表示します。ザ・amplitude その電圧信号のは一定ですが、電圧信号を垂直方向にカバーする分割数を変えることで変えることができます volt/divisionCROパネルのノブ。したがって、amplitude 次の式を使用して、CROの画面に表示される信号の

$$ A = j \ times n_ {v} $$

どこ、

$ A $は振幅です

$ j $はボルト/除算の値です

$ n_ {v} $は、垂直方向の信号をカバーする分割数です。

期間の測定

CROは、電圧信号を時間の関数として画面に表示します。ザ・Time period その周期的な電圧信号のは一定ですが、水平方向の電圧信号の1つの完全なサイクルをカバーする分割数を変更することで変更できます time/division CROパネルのノブ。

したがって、 Time period 次の式を使用して、CROの画面に表示される信号の

$$ T = k \ times n_ {h} $$

どこ、

$ T $は期間です

$ j $は時間/分割の値です

$ n_ {v} $は、水平方向の周期信号の1つの完全なサイクルをカバーする分割数です。

周波数の測定

周期信号の周波数fは、時間Tの逆数です。 Mathematically、次のように表すことができます

$$ f = \ frac {1} {T} $$

したがって、これらの2つの手順に従うことで、周期信号の周波数fを見つけることができます。

• Step1 −を見つける Time period 周期信号の

• Step2 −取る reciprocal ステップ1で得られる周期信号の期間の

次の章では、特殊用途のオシロスコープについて説明します。

前の章では、基本的なオシロスコープであるブラウン管オシロスコープ（CRO）について説明しました。要件に基づいて、基本的なオシロスコープにいくつかの追加ブロックを含めるだけで、専用のオシロスコープを入手できます。

以下は special purpose oscilloscopes。

• デュアルビームオシロスコープ
• デュアルトレースオシロスコープ
• デジタルストレージオシロスコープ

それでは、これらの専用オシロスコープについて1つずつ説明しましょう。

デュアルビームオシロスコープ

2つの電圧波形を表示するオシロスコープは、デュアルビームオシロスコープと呼ばれます。そのblock diagram 下図に示します。

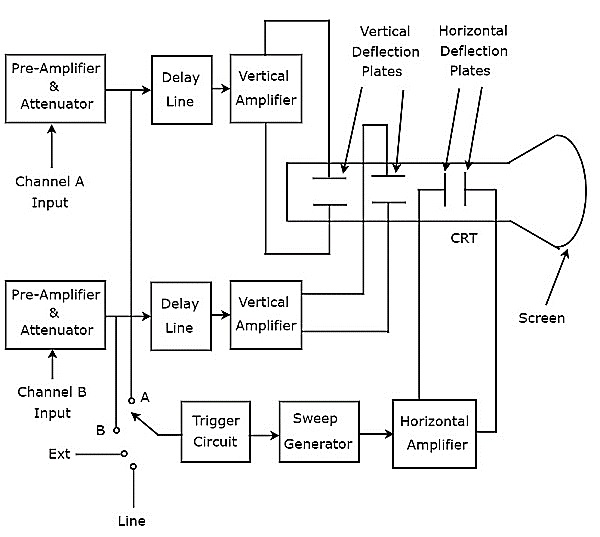
上図に示すように、デュアルビームオシロスコープのCRTは、2セットの垂直偏向板と1セットの水平偏向板で構成されています。

次のブロックを組み合わせたものを、 channel。

• プリアンプ＆アッテネーター
• ディレイライン
• 垂直増幅器
• 垂直偏向板のセット

デュアルビームオシロスコープには2つのチャネルがあります。したがって、2つの信号、つまりAとBをそれぞれチャネルAとチャネルBの入力として適用できます。これらの4つの信号のいずれかを次のように選択できますtrigger inputスイッチを使用してトリガー回路に接続します。これらは、入力信号A＆B、外部信号（Ext）、およびライン入力です。

このオシロスコープは、2対の垂直偏向板があるため、2つの垂直偏向ビームを生成します。このオシロスコープでは、ビームを水平方向に偏向させるのに役立つブロックが両方の入力信号に共通です。最後に、このオシロスコープはtwo input signals CRTの画面で同時に。

デュアルトレースオシロスコープ

画面に2つのトレースを生成するオシロスコープは、デュアルトレースオシロスコープと呼ばれます。そのblock diagram 下図に示します。

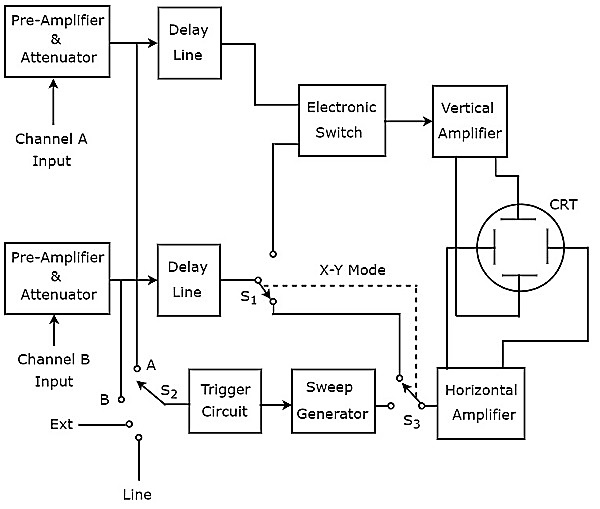
上図に示すように、デュアルトレースオシロスコープのCRTは、垂直偏向板のセットと水平偏向板の別のセットで構成されています。チャネルは、プリアンプとアッテネーター、ディレイライン、垂直アンプ、垂直偏向板の4つのブロックで構成されています。

上記のブロック図では、最初の2つのブロックが両方のチャネルに別々に存在しています。最後の2つのブロックは、両方のチャネルに共通です。したがって、の助けを借りてelectronic switch 特定のチャンネルの遅延線出力を垂直増幅器に接続できます。

これらの4つの信号のいずれかをトリガー入力として選択できます。 trigger circuitスイッチを使用して。これらは、入力信号A＆B、外部信号（Ext）、およびライン入力です。

このオシロスコープは、同じ電子ビームを使用して、電子スイッチを使用して入力信号AとBを垂直方向に偏向し、 two traces。ビームを水平方向に偏向するブロックは、両方の入力信号に共通です。

デジタルストレージオシロスコープ

波形をデジタルで保存するオシロスコープは、デジタルストレージオシロスコープとして知られています。ザ・block diagram （デジタル）ストレージオシロスコープの

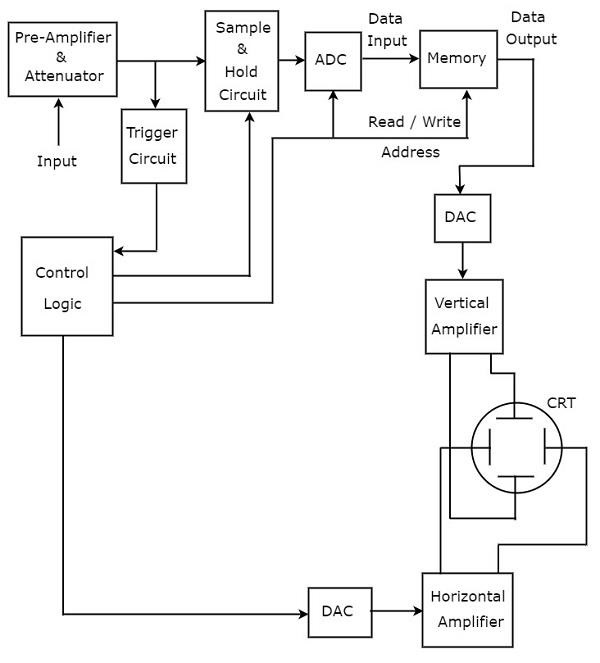
デジタルデータストレージに必要な追加のブロックが基本的なオシロスコープに追加され、デジタルストレージオシロスコープに変換されます。に必要なブロックstoring of digital dataデジタルストレージオシロスコープのプリアンプとアッテネーターと垂直アンプの間にあります。それらは、サンプルアンドホールド回路、アナログ-デジタルコンバーター（ADC）、メモリー＆デジタル-アナログコンバーターです。

Control logicさまざまな制御信号を送信することにより、最初の3つのブロックを制御します。制御ロジックやデジタル-アナログコンバータなどのブロックは、デジタルストレージオシロスコープのトリガー回路と水平増幅器の間に存在します。

デジタルストレージオシロスコープ stores the data画面に波形を表示する前にデジタルで。一方、基本的なオシロスコープにはこの機能はありません。

Lissajous figureは、CROの水平偏向板と垂直偏向板の両方に正弦波信号が適用されたときに画面に表示されるパターンです。これらのパターンは、CROの水平偏向板と垂直偏向板の両方に適用される正弦波信号の振幅、周波数、および位相差に基づいて変化します。

次の図は、 example リサージュ図形の。

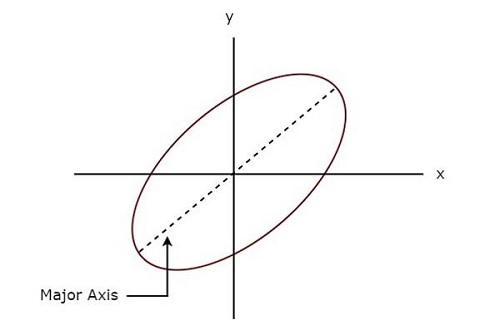
上記のリサージュ図形は elliptical shape その主軸には、正のx軸を持つ傾斜角があります。

リサージュ図形を使用した測定

私たちは次のことができます two measurements リサージュ図形から。

• 正弦波信号の周波数
• 2つの正弦波信号間の位相差

ここで、これら2つの測定値について1つずつ説明します。

周波数の測定

正弦波信号がCROの水平偏向板と垂直偏向板の両方に適用されると、リサージュ図形が画面に表示されます。したがって、標準の正弦波信号を適用しますknown frequencyCROの水平偏向板に。同様に、正弦波信号を適用します。frequency です unknown CROの垂直偏向板に

$ f_ {H} $と$ f_ {V} $を正弦波信号の周波数とし、それぞれCROの水平偏向板と垂直偏向板に適用します。$ f_ {H} $と$ f_ {V} $の関係は次のようになります。mathematically 以下のように表されます。

$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$

上記の関係から、CROの垂直偏向板に適用される正弦波信号の周波数を取得します。

$ f_ {V} = \ left（\ frac {n_ {H}} {n_ {V}} \ right）f_ {H} $ （式1）

どこ、

$ n_ {H} $は水平方向の接線の数です

$ n_ {V} $は垂直接線の数です

リサージュ図形から$ n_ {H} $と$ n_ {V} $の値を見つけることができます。したがって、式1に$ n_ {H} $、$ n_ {V} $、および$ f_ {H} $の値を代入すると、次の値が得られます。$f_{V}$、すなわち frequency of sinusoidal signal これは、CROの垂直偏向板に適用されます。

位相差の測定

正弦波信号がCROの水平偏向板と垂直偏向板の両方に適用されると、リサージュ図形が画面に表示されます。したがって、正弦波信号を適用します。same amplitude and frequency CROの水平および垂直偏向板の両方に。

形状に基づくいくつかのリサージュ図形の場合、2つの正弦波信号間の位相差を直接知ることができます。

• リサージュ図形が straight line 正のx軸で$ 45 ^ {\ circ} $の傾きで、次に phase difference2つの正弦波信号の間は$ 0 ^ {\ circ} $になります。つまり、これら2つの正弦波信号の間に位相差はありません。

• リサージュ図形が straight line 正のx軸で$ 135 ^ {\ circ} $の傾きで、次に phase difference2つの正弦波信号の間は$ 180 ^ {\ circ} $になります。つまり、これら2つの正弦波信号は位相がずれています。

• リサージュ図形が circular shapeの場合、2つの正弦波信号間の位相差は$ 90 ^ {\ circ} $または$ 270 ^ {\ circ} $になります。

リサージュ図形が次の場合、式を使用して2つの正弦波信号間の位相差を計算できます。 elliptical shape。

• 傾斜角を持つ楕円形のリサージュ図形の主軸が正のx軸で$ 0 ^ {\ circ} $と$ 90 ^ {\ circ} $の間にある場合、2つの正弦波信号間の位相差はになります。

$$ \ phi = \ sin ^ {-1} \ left（\ frac {x_ {1}} {x_ {2}} \ right）= \ sin ^ {-1} \ left（\ frac {y_ {1} } {y_ {2}} \ right）$$

• 傾斜角を持つ楕円形のリサージュ図形の主軸が正のx軸で$ 90 ^ {\ circ} $と$ 180 ^ {\ circ} $の間にある場合、2つの正弦波信号間の位相差はになります。

$$ \ phi = 180- \ sin ^ {-1} \ left（\ frac {x_ {1}} {x_ {2}} \ right）= 180- \ sin ^ {-1} \ left（\ frac { y_ {1}} {y_ {2}} \ right）$$

Where,

$ x_ {1} $は、原点からx軸上の点までの距離であり、楕円形のリサージュ図形が交差します。

$ x_ {2} $は、原点から楕円形のリサージュ図形の垂直接線までの距離です。

$ y_ {1} $は、原点からy軸上の点までの距離で、楕円形のリサージュ図形が交差します。

$ y_ {2} $は、原点から楕円形のリサージュ図形の水平接線までの距離です。

この章では、式を使用して、未知の正弦波信号の周波数と、リサージュ図形から2つの正弦波信号間の位相差を見つける方法を学習します。

プローブを介して、任意のテスト回路をオシロスコープに接続できます。CROは基本的なオシロスコープであるため、それに接続されているプローブはCRO probe。

テスト回路に負荷の問題が発生しないようにプローブを選択する必要があります。これにより、CRO画面の信号でテスト回路を適切に分析できます。

CROプローブには次のものが必要です characteristics。

• 高インピーダンス
• 高帯域幅

ザ・ block diagram CROプローブの概要を下図に示します。

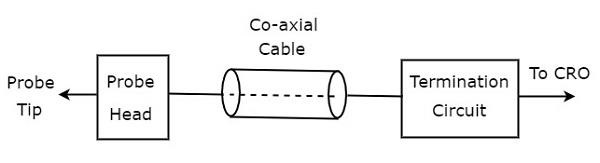
図に示すように、CROプローブは主に3つのブロックで構成されています。それらは、プローブヘッド、同軸ケーブル、および終端回路です。同軸ケーブルは、プローブヘッドと終端回路を接続するだけです。

CROプローブの種類

CROプローブは次のように分類できます。 two types。

• パッシブプローブ
• アクティブプローブ

ここで、これら2種類のプローブについて1つずつ説明します。

パッシブプローブ

プローブヘッドがパッシブエレメントで構成されている場合、それは passive probe。パッシブプローブの回路図を下図に示します。

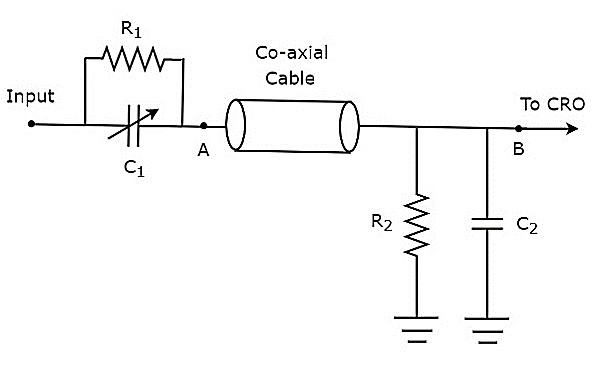
図に示すように、プローブヘッドは、抵抗$ R_ {1} $と可変コンデンサ$ C_ {1} $の並列組み合わせで構成されています。同様に、終端回路は、抵抗$ R_ {2} $とコンデンサ$ C_ {2} $の並列組み合わせで構成されています。

上記の回路図は、次の形式に変更されています。 bridge circuit 下の図に示します。

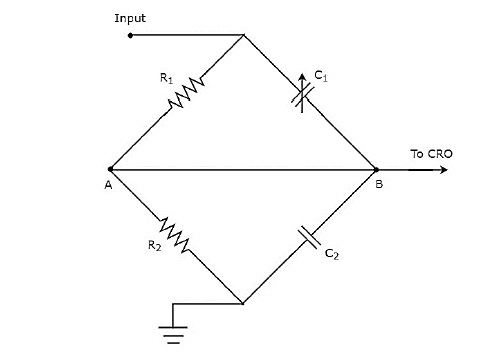
可変コンデンサ$ c_ {1} $の値を調整することにより、ブリッジのバランスをとることができます。次の章では、ブリッジの概念について説明します。とりあえず、次のことを考慮してください。balancing condition of AC bridge。

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

Substitute、インピーダンス$ Z_ {1}、Z_ {2}、Z_ {3} $および$ Z_ {4} $ as $ R_ {1}、\ frac {1} {j \ omega C_ {1}}、R_ {上記の式では、それぞれ2} $と$ \ frac {1} {j \ omega C_ {2}} $です。

$$ R_ {1} \ left（\ frac {1} {j \ omega C_ {2}} \ right）= \ left（\ frac {1} {j \ omega C_ {1}} \ right）R_ {2 } $$

$ \ Rightarrow R_ {1} C_ {1} = R_ {2} C_ {2} $式1

分圧原理により、 voltage across resistor, $R_{2}$ なので

$$ V_ {0} = V_ {i} \ left（\ frac {R_ {2}} {R_ {1} + R_ {2}} \ right）$$

attenuation factorは、入力電圧$ V_ {i} $と出力電圧$ V_ {0} $の比率です。したがって、上記の式から、減衰係数$ \ alpha $を次のように取得します。

$$ \ alpha = \ frac {V_ {i}} {V_ {0}} = \ frac {R_ {1} + R_ {2}} {R_ {2}} $$

$ \ Rightarrow \ alpha = 1+ \ frac {R_ {1}} {R_ {2}} $

$ \ Rightarrow \ alpha-1 = \ frac {R_ {1}} {R_ {2}} $

$ \ Rightarrow R_ {1} = \ left（\ alpha-1 \ right）R_ {2} $式2

式2から、$ R_ {1} $の値は、$ \：\ alpha> 1 $の整数値の場合、ð?? '…2の値以上であると結論付けることができます。

式1に式2を代入します。

$$ \ left（\ alpha-1 \ right）R_ {2} C_ {1} = R_ {2} C_ {2} $$

$ \ Rightarrow \ left（\ alpha-1 \ right）C_ {1} = C_ {2} $

$ \ Rightarrow C_ {1} = \ frac {C_ {2}} {\ left（\ alpha-1 \ right）} $式3

式3から、$ \ alpha> 1 $の整数値の場合、$ C_ {1} $の値は$ C_ {2} $の値以下であると結論付けることができます。

Example

減衰係数$ \ alpha $が10であるプローブの$ R_ {1} $と$ C_ {1} $の値を見つけましょう。$ R_ {2} = 1 M \ Omega $と$ C_と仮定します。 {2} = 18pF $。

• Step1 −式2の$ \ alpha $と$ R_ {2} $の値を代入することにより、$ R_ {1} $の値を取得します。

$$ R_ {1} = \ left（10-1 \ right）\ times 1 \ times 10 ^ {6} $$

$$ \ Rightarrow R_ {1} = 9 \ times 10 ^ {6} $$

$$ \ Rightarrow R_ {1} = 9 M \ Omega $$

Step 2 −式3に$ \ alpha $と$ C_ {2} $の値を代入することにより、$ C_ {1} $の値を取得します。

$$ C_ {1} = \ frac {18 \ times10 ^ {-12}} {\ left（10-1 \ right）} $$

$$ \ Rightarrow C_ {1} = 2 \ times 10 ^ {-12} $$

$$ \ Rightarrow C_ {1} = 2 pF $$

したがって、プローブの$ R_ {1} $と$ C_ {1} $の値は、指定された仕様に対してそれぞれ$ 9M \ Omega $と$ 2pF $になります。

アクティブプローブ

プローブヘッドがアクティブな電子部品で構成されている場合、それはと呼ばれます active probe。アクティブプローブのブロック図を下図に示します。

図に示すように、プローブヘッドはBJTエミッタフォロワとカスケード接続されたFETソースフォロワで構成されています。FETソースフォロワは、高い入力インピーダンスと低い出力インピーダンスを提供します。一方、BJTエミッタフォロワの目的は、インピーダンスの不一致を回避または排除することです。

同軸ケーブルや終端回路などの他の2つの部分は、アクティブプローブとパッシブプローブの両方で同じままです。

電気部品がブリッジまたはリング構造の形で配置されている場合、その電気回路は bridge。一般に、ブリッジは4つのアームまたはブランチのセットでループを形成します。各ブランチには、1つまたは2つの電気コンポーネントが含まれる場合があります。

橋の種類

ブリッジ回路またはブリッジは、それらを操作できる電圧信号に基づいて、次の2つのカテゴリに分類できます。

• DCブリッジ
• ACブリッジ

それでは、これら2つのブリッジについて簡単に説明しましょう。

DCブリッジ

ブリッジ回路がDC電圧信号のみで動作できる場合、それはDCブリッジ回路または単に DC bridge。DCブリッジは、未知の抵抗の値を測定するために使用されます。ザ・circuit diagram DCブリッジの図は下図のようになります。

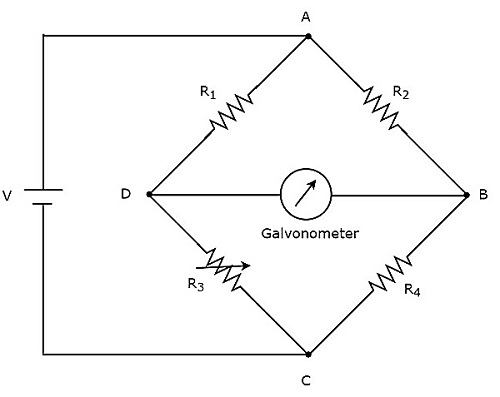
上記のDCブリッジには four arms各アームは抵抗で構成されています。このうち、2つの抵抗は固定抵抗値を持ち、1つの抵抗は可変抵抗で、もう1つは未知の抵抗値を持ちます。

上記のDCブリッジ回路は、 DC voltage sourceそれを1つの対角線に配置することによって。検流計は、DCブリッジのもう一方の対角線に配置されます。橋が不均衡である限り、それはいくらかのたわみを示します。

検流計がゼロ（ゼロ）のたわみを示すまで、可変抵抗器の抵抗値を変化させます。さて、上記のDCブリッジはバランスの取れたものと言われています。だから、私たちはの値を見つけることができますunknown resistance 節点方程式を使用する。

ACブリッジ

ブリッジ回路がAC電圧信号のみで動作できる場合、それはACブリッジ回路または単に AC bridge。ACブリッジは、未知のインダクタンス、静電容量、および周波数の値を測定するために使用されます。

ザ・ circuit diagram ACブリッジの図は下図のようになります。

ACブリッジの回路図はDCブリッジの回路図と似ています。上記のACブリッジにはfour arms各アームはある程度のインピーダンスで構成されています。つまり、各アームには、抵抗、インダクタ、コンデンサなどのパッシブ要素の単一または組み合わせがあります。

4つのインピーダンスのうち、2つのインピーダンスは固定値であり、1つのインピーダンスは可変で、もう1つは未知のインピーダンスです。

上記のACブリッジ回路は、 AC voltage sourceそれを1つの対角線に配置することによって。検出器は、ACブリッジのもう一方の対角線に配置されます。橋が不均衡である限り、それはいくらかのたわみを示します。

上記のACブリッジ回路は、 AC voltage sourceそれを1つの対角線に配置することによって。検出器は、ACブリッジのもう一方の対角線に配置されます。橋が不均衡である限り、それはいくらかのたわみを示します。

検出器がヌル（ゼロ）のたわみを示すまで、可変インピーダンスのインピーダンス値を変化させます。さて、上記のACブリッジはバランスの取れたものと言われています。だから、私たちはの値を見つけることができますunknown impedance バランスの取れた状態を使用することによって。

DC bridgesDC電圧信号のみで操作できます。DCブリッジは、ブリッジに存在する未知の抵抗の値を測定するのに役立ちます。ホイートストンブリッジはDCブリッジの一例です。

さて、について話し合いましょう Wheatstone’s Bridge 未知の抵抗値を見つけるために。

ホイートストンブリッジ

ホイートストンブリッジは単純なDCブリッジで、主に4本のアームがあります。これらの4つのアームはひし形または正方形の形状を形成し、各アームは1つの抵抗で構成されます。

未知の抵抗の値を見つけるには、検流計とDC電圧源が必要です。したがって、これら2つの一方はホイートストンブリッジの一方の対角線に配置され、もう一方はホイートストンブリッジのもう一方の対角線に配置されます。

ホイートストンブリッジは、中程度の抵抗の値を測定するために使用されます。ザ・circuit diagram ホイートストンブリッジの概要を下図に示します。

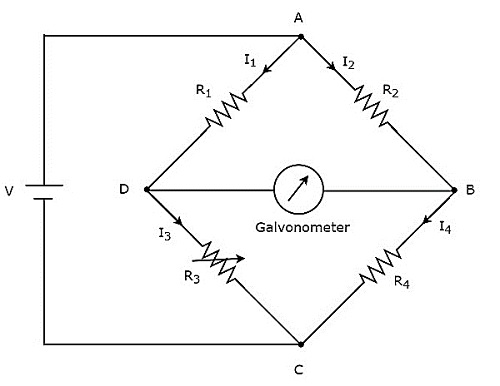
上記の回路では、アームAB、BC、CD、およびDAが一緒になって rhombusまたは正方形の形。これらは、それぞれ抵抗$ R_ {2} $、$ R_ {4} $、$ R_ {3} $、および$ R_ {1} $で構成されています。これらの抵抗アームを流れる電流をそれぞれ$ I_ {2} $、$ I_ {4} $、$ I_ {3} $、$ I_ {1} $とし、これらの電流の方向を図に示します。

対角アームDBとACは、それぞれVボルトの検流計とDC電圧源で構成されています。ここで、抵抗$ R_ {3} $は標準の可変抵抗であり、抵抗$ R_ {4} $は未知の抵抗です。私たちはできるbalance the bridge、抵抗器の抵抗値を変えることにより、$ R_ {3} $。

上記のブリッジ回路は、対角アームDBに電流が流れていないときにバランスが取れています。つまり、no deflection 検流計で、ブリッジのバランスが取れているとき。

次の場合、ブリッジはバランスが取れます two conditions 満足しています。

• アームADの両端の電圧はアームABの両端の電圧に等しくなります。すなわち、

$$ V_ {AD} = V_ {AB} $$

$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $式1

• アームDCの両端の電圧は、アームBCの両端の電圧に等しくなります。すなわち、

$$ V_ {DC} = V_ {BC} $$

$ \ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4} $式2

上記の2つのバランス条件から、次のようになります。 two conclusions.

• アームADを流れる電流はアームDCの電流と等しくなります。すなわち、

$$ I_ {1} = I_ {3} $$

• アームABを流れる電流は、アームBCの電流と等しくなります。すなわち、

$$ I_ {2} = I_ {4} $$

式1と式2の比率を取ります。

$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $式3

式3の$ I_ {1} = I_ {3} $と$ I_ {2} = I_ {4} $を代入します。

$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$

$$ \ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$

$$ \ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

上記の式に抵抗$ R_ {1} $、$ R_ {2} $、$ R_ {3} $の既知の値を代入すると、次の式が得られます。 value of resistor,$R_{4}$。

この章では、インダクタンスの測定に使用できるACブリッジについて説明します。ACブリッジは、AC電圧信号のみで動作します。ザ・circuit diagram ACブリッジの概要を下図に示します。

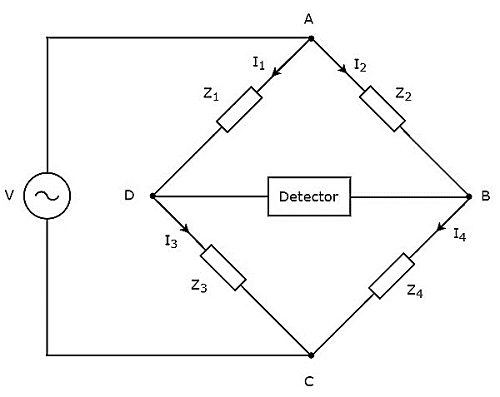
上図に示すように、ACブリッジは主に4つのアームで構成されており、これらはひし形または square shape。これらのアームはすべて、ある程度のインピーダンスで構成されています。

未知のインピーダンスの値を見つけるために、検出器とAC電圧源も必要です。したがって、これら2つの一方はACブリッジの一方の対角線に配置され、もう一方はACブリッジのもう一方の対角線に配置されます。ホイートストンブリッジの平衡状態-

$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

取得します balancing condition of AC bridge、上記の式でRをZに置き換えるだけです。

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $

ここで、$ Z_ {1} $と$ Z_ {2} $は固定インピーダンスです。一方、$ Z_ {3} $は標準の可変インピーダンスであり、$ Z_ {4} $は未知のインピーダンスです。

Note −アプリケーションに基づいて、これら4つのインピーダンスのいずれか2つを固定インピーダンス、1つのインピーダンスを標準可変インピーダンス、もう1つのインピーダンスを未知のインピーダンスとして選択できます。

以下は、測定に使用できる2つのACブリッジです。 inductance。

• マクスウェルブリッジ
• ヘイズブリッジ

それでは、これら2つのACブリッジについて1つずつ説明しましょう。

マクスウェルブリッジ

マクスウェルブリッジは、ひし形または菱形で接続された4本のアームを備えたACブリッジです。 square shape。このブリッジの2つのアームは単一の抵抗で構成され、一方のアームは抵抗とインダクタの直列の組み合わせで構成され、もう一方のアームは抵抗とコンデンサの並列の組み合わせで構成されます。

未知のインピーダンスの値を見つけるために、AC検出器とAC電圧源が使用されます。したがって、これら2つの一方はマクスウェルブリッジの一方の対角線に配置され、もう一方はマクスウェルブリッジのもう一方の対角線に配置されます。

マクスウェルブリッジは、中程度のインダクタンスの値を測定するために使用されます。ザ・circuit diagram マクスウェルブリッジの図を下図に示します。

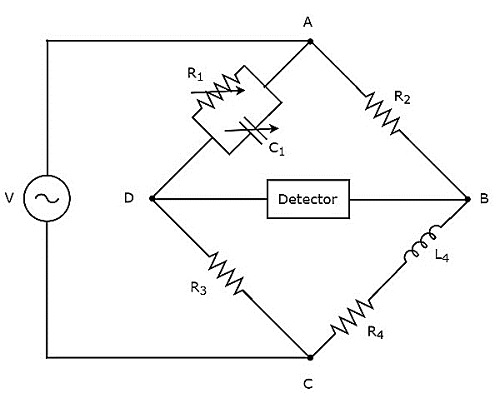
上記の回路では、アームAB、BC、CD、およびDAが一緒になって菱形または正方形の形状を形成します。アームABとCDは、それぞれ$ R_ {2} $と$ R_ {3} $の抵抗で構成されています。アームBCは、抵抗$ R_ {4} $とインダクタ$ L_ {4} $の直列の組み合わせで構成されています。アームDAは、抵抗$ R_ {1} $とコンデンサ$ C_ {1} $の並列組み合わせで構成されています。

$ Z_ {1}、Z_ {2}、Z_ {3} $、および$ Z_ {4} $を、それぞれアームDA、AB、CD、およびBCのインピーダンスとします。ザ・values of these impedances になります

$$ Z_ {1} = \ frac {R_ {1} \ left（\ frac {1} {j \ omega C_ {1}} \ right）} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$

$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute ACブリッジの次の平衡状態でのこれらのインピーダンス値。

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left（{\ frac {R_ {1}} 1 + j \ omega R_ {1} C_ {1}}} \ right）} $$

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left（1 + j \ omega R_ {1} C_ {1} \ right）} {R_ { 1}} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $

沿って comparing 上記の方程式のそれぞれの実数と虚数の項は、次のようになります。

$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $式1

$ L_ {4} = C_ {1} R_ {2} R_ {3} $式2

式1に抵抗$ R_ {1} $、$ R_ {2} $、および$ R_ {3} $の値を代入すると、抵抗$ R_ {4} $の値が得られます。同様に、式2にコンデンサの値$ C_ {1} $と抵抗の値$ R_ {2} $と$ R_ {3} $を代入すると、インダクタの値$ L_ {4が得られます。 } $。

ザ・ advantage マクスウェルブリッジの特徴は、抵抗$ R_ {4} $とインダクタ$ L_ {4} $の両方の値が周波数の値に依存しないことです。

ヘイズブリッジ

ヘイズブリッジはマクスウェルブリッジの修正版であり、マクスウェルブリッジの抵抗とコンデンサの直列の組み合わせで構成されるアームへの抵抗とコンデンサの並列の組み合わせで構成されるアームを変更することで得られます。

ヘイのブリッジは、高インダクタンスの値を測定するために使用されます。ザ・circuit diagram ヘイの橋の様子を下図に示します。

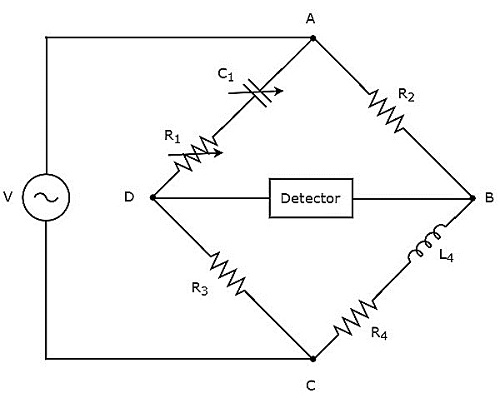
上記の回路では、アームAB、BC、CD、およびDAが一緒になって菱形または正方形の形状を形成します。アームABとCDは、それぞれ$ R_ {2} $と$ R_ {3} $の抵抗で構成されています。アームBCは、抵抗$ R_ {4} $とインダクタ$ L_ {4} $の直列の組み合わせで構成されています。アームDAは、抵抗$ R_ {1} $とコンデンサ$ C_ {1} $の直列の組み合わせで構成されています。

$ Z_ {1}、Z_ {2}、Z_ {3} $、および$ Z_ {4} $を、それぞれアームDA、AB、CD、およびBCのインピーダンスとします。ザ・values of these impedances になります

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute ACブリッジの次の平衡状態でのこれらのインピーダンス値。

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left（\ frac {1 + j \ omega R_ {1} C_ {1}} {j \オメガC_ {1}} \ right）} $

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left（1 + j \ omega R_ {1} C_ {1} \ right）} $

上記の式の右辺の項の分子と分母に$ 1-j \ omega R_ {1} C_ {1} $を掛けます。

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left（1 + j \ omega R_ {1} C_ { 1} \ right）} \ times \ frac {\ left（1-j \ omega R_ {1} C_ {1} \ right）} {\ left（1-j \ omega R_ {1} C_ {1} \ right ）} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \オメガR_ {2} R_ {3} C_ {1}} {\ left（1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right）} $

沿って comparing 上記の方程式のそれぞれの実数と虚数の項は、次のようになります。

$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left（1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right）} $式3

$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left（1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right）} $式4

式3と式4に$ R_ {1}、R_ {2}、R_ {3}、C_ {1} $、$ \ omega $の値を代入すると、抵抗の値$ R_ {4が得られます。 } $とインダクタ、$ L_ {4} $。

前の章では、インダクタンスの測定に使用できる2つのACブリッジについて説明しました。この章では、次のことについて説明しますtwo AC bridges。

• シェリングブリッジ
• ウィーンブリッジ

これらの2つのブリッジは、それぞれ静電容量と周波数を測定するために使用できます。

シェリングブリッジ

シェリングブリッジは、ひし形または菱形で接続された4つのアームを備えたACブリッジです。 square shape、一方のアームは単一の抵抗で構成され、一方のアームは抵抗とコンデンサの直列の組み合わせで構成され、一方のアームは単一のコンデンサで構成され、もう一方のアームは抵抗とコンデンサの並列の組み合わせで構成されます。

AC検出器とAC電圧源は、未知のインピーダンスの値を見つけるためにも使用されるため、一方はシェリングブリッジの一方の対角線に配置され、もう一方はシェリングブリッジのもう一方の対角線に配置されます。

シャーリングブリッジは、静電容量の値を測定するために使用されます。ザ・circuit diagram シェリング橋の様子を下図に示します。

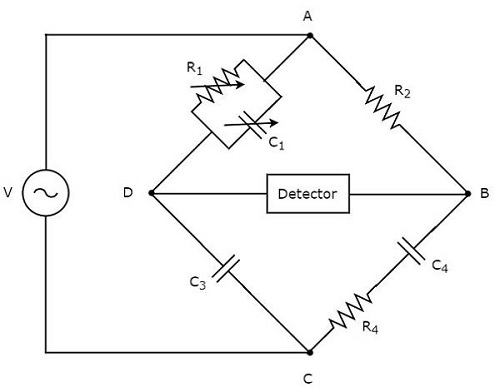
上記の回路では、アームAB、BC、CD、およびDAが一緒にひし形を形成します。 square shape。アームABは、抵抗$ R_ {2} $で構成されています。アームBCは、抵抗$ R_ {4} $とコンデンサ$ C_ {4} $の直列の組み合わせで構成されています。アームCDは、コンデンサ$ C_ {3} $で構成されています。アームDAは、抵抗$ R_ {1} $とコンデンサ$ C_ {1} $の並列組み合わせで構成されています。

$ Z_ {1} $、$ Z_ {2} $、$ Z_ {3} $、および$ Z_ {4} $は、それぞれアームDA、AB、CD、およびBCのインピーダンスです。ザ・values of these impedances になります

$ Z_ {1} = \ frac {R_ {1} \ left（\ frac {1} {j \ omega C_ {1}} \ right）} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $

$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $

$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $

$ \ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $

Substitute ACブリッジの次の平衡状態でのこれらのインピーダンス値。

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left（\ frac {1} {j \ omega C_ { 3}} \ right）} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$

$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left（1 + j \ omega R_ {1} C_ {1} \ right）} {j \ omega R_ {1} C_ {3}} $

$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left（1 + j \ omega R_ {1} C_ {1} \ right）} {R_ {1} C_ {3}} $

$ \ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $

沿って comparing 上記の方程式のそれぞれの実数と虚数の項は、次のようになります。

$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $式1

$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $式2

式1に$ R_ {1}、R_ {2} $、および$ C_ {3} $の値を代入すると、コンデンサの値$ C_ {4} $が得られます。同様に、式2に$ R_ {2}、C_ {1} $、および$ C_ {3} $の値を代入すると、抵抗の値$ R_ {4} $が得られます。

ザ・ advantage Scheringブリッジの特徴は、抵抗$ R_ {4} $とコンデンサ$ C_ {4} $の両方の値が周波数の値に依存しないことです。

ウィーンブリッジ

Wien’s bridgeは、ひし形または正方形の形で接続された4本のアームを持つACブリッジです。2つのアームは単一の抵抗で構成され、一方のアームは抵抗とコンデンサの並列の組み合わせで構成され、もう一方のアームは抵抗とコンデンサの直列の組み合わせで構成されます。

周波数の値を見つけるには、AC検出器とAC電圧源も必要です。したがって、これら2つの一方はウィーンブリッジの一方の対角線に配置され、もう一方はウィーンブリッジのもう一方の対角線に配置されます。

ザ・ circuit diagram ウィーンブリッジの様子を下図に示します。

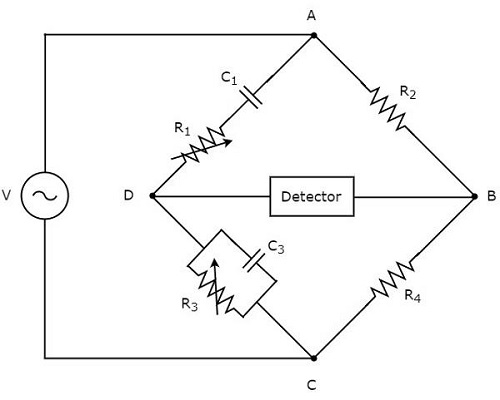
上記の回路では、アームAB、BC、CD、およびDAが一緒にひし形を形成します。 square shape。アームABとBCは、それぞれ$ R_ {2} $と$ R_ {4} $の抵抗で構成されています。アームCDは、抵抗$ R_ {3} $とコンデンサ$ C_ {3} $の並列組み合わせで構成されています。アームDAは、抵抗$ R_ {1} $とコンデンサ$ C_ {1} $の直列の組み合わせで構成されています。

$ Z_ {1}、Z_ {2}、Z_ {3} $、および$ Z_ {4} $を、それぞれアームDA、AB、CD、およびBCのインピーダンスとします。ザ・values of these impedances になります

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$

$ Z_ {2} = R_ {2} $

$$ Z_ {3} = \ frac {R_ {3} \ left（\ frac {1} {j \ omega C_ {3}} \ right）} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$

$$ \ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$

$ Z_ {4} = R_ {4} $

Substitute ACブリッジの次の平衡状態でのこれらのインピーダンス値。

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

$$ \ left（\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right）R_ {4} = R_ {2} \ left（\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ right）$$

$ \ Rightarrow \ left（1 + j \ omega R_ {1} C_ {1} \ right）\ left（1 + j \ omega R_ {3} C_ {3} \ right）R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Rightarrow \ left（1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1}-\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right）R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Rightarrow R_ {4} \ left（\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right）+ j \ omega R_ {4} \ left（R_ {3} C_ {3} + R_ {1} C_ {1} \ right）= j \ omega C_ {1} R_ {2} R_ {3} $

Equate それぞれ real terms 上記の式の。

$$ R_ {4} \ left（1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right）= 0 $$

$ \ Rightarrow 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $

$ \ Rightarrow 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $

$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

Substitute、$ \ omega = 2 \ pi f $上記の式。

$$ \ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$

$ \ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

上記の式に$ R_ {1}、R_ {3}、C_ {1} $、および$ C_ {3} $の値を代入することにより、周波数の値、AC電圧源の$ f $を見つけることができます。

$ R_ {1} = R_ {3} = R $および$ C_ {1} = C_ {3} = C $の場合、次の式を使用して、周波数の値、AC電圧源の$ f $を見つけることができます。 。

$$ f = \ frac {1} {2 \ pi RC} $$

ワインの橋は主に frequency value AF範囲の。

基本的に、トランスデューサーはある形式のエネルギーを別の形式のエネルギーに変換します。非電気的形態のエネルギーを電気的形態のエネルギーに変換するトランスデューサーは、electrical transducer。ザ・block diagram 電気変換器の概要を下図に示します。

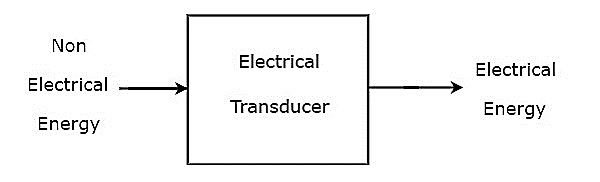
図に示すように、電気変換器は電気エネルギーを持つ出力を生成します。電気変換器の出力は、非電気エネルギーを持つ入力と同等です。

電気変換器の種類

主に、電気変換器は次のように分類できます。 two types。

• アクティブトランスデューサー
• パッシブトランスデューサー

ここで、これら2種類のトランスデューサーについて簡単に説明します。

アクティブトランスデューサー

電圧や電流などの電気量の1つを生成できるトランスデューサは、 active transducer。外部電源を必要としないため、自己生成トランスデューサとも呼ばれます。

ザ・ block diagram アクティブなトランスデューサーの例を下の図に示します。

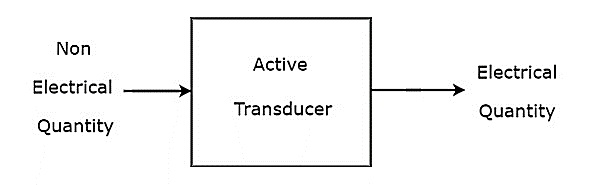
図に示すように、アクティブなトランスデューサーは、非電気的な入力量（または信号）と同等の電気的な量（または信号）を生成します。

Examples

以下は、アクティブなトランスデューサーの例です。

• ピエゾ電気トランスデューサ
• 光電変換器
• 熱電変換器

これらのアクティブトランスデューサについては、次の章で説明します。

パッシブトランスデューサー

電圧や電流などの電気量を生成できないトランスデューサーは、 passive transducer。ただし、抵抗（R）、インダクタ（L）、コンデンサ（C）などの受動素子の1つに変動が生じます。パッシブトランスデューサには外部電源が必要です。

ザ・ block diagram パッシブトランスデューサの概要を下図に示します。

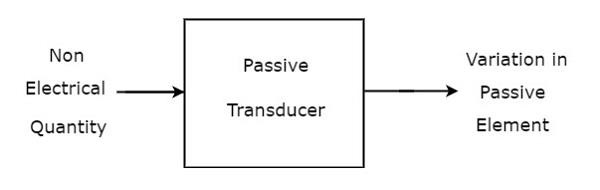
図に示すように、パッシブトランスデューサは、非電気入力量（または信号）の変化に応じてパッシブエレメントに変化を生じます。

Examples

以下はパッシブトランスデューサーの例です。

• 抵抗膜トランスデューサ
• 誘導トランスデューサ
• 容量性トランスデューサー

これらのパッシブトランスデューサについては、後の章で説明します。

Active transducer非電気量を電気量に変換するトランスデューサーです。圧力、光の照明、温度などの非電気的な量を考えてみましょう。したがって、選択した非電気量に応じて、次の3つのアクティブなトランスデューサーを取得します。

• ピエゾ電気トランスデューサ
• 光電変換器
• 熱電変換器

それでは、これら3つのアクティブなトランスデューサーについて1つずつ説明しましょう。

ピエゾ電気トランスデューサ

アクティブなトランスデューサーは piezo electric transducer、入力圧力に相当する電気量を生成する場合。次の3つの物質は圧電効果を示します。

• Quartz
• ロシェル塩
• Tourmaline

これら3つの物質が示す圧電効果は、トルマリン塩、石英塩、ロシェル塩の順です。これらの3つの物質による機械的強度の昇順は、ロシェル塩、石英、トルマリンです。

Quartz は、中程度の圧電効果を示し、これら3つの圧電物質の中で中程度の機械的強度を持っているため、圧電トランスデューサとして使用されます。

クォーツトランスデューサー

ザ・ circuit diagram石英トランスデューサーの概要を下図に示します。図に示すように、水晶振動子はベースと力加算部材の間に配置されています。出力電圧は、水晶の両面に配置された金属電極で測定できます。

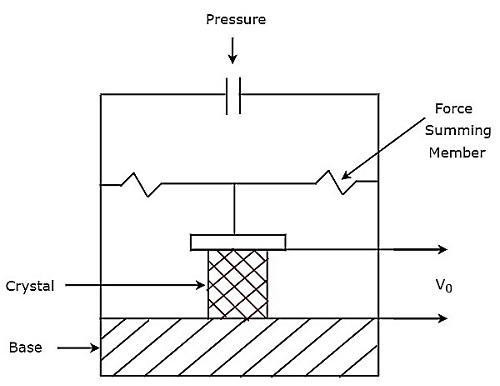
ザ・ output voltage、上記の圧力トランスデューサの$ V_ {0} $は

$$ V_ {0} = \ frac {Q} {C} $$

光電変換器

アクティブトランスデューサは、光入力の照明と同等の電気量を生成する場合、光電トランスデューサと呼ばれます。ザ・circuit diagram 光電変換器の概要を下図に示します。

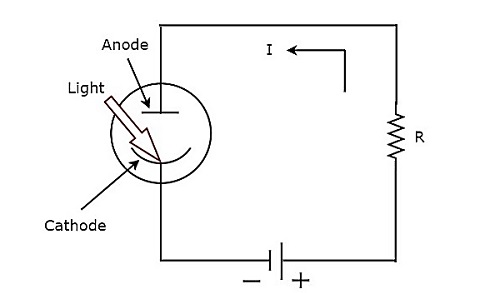
ザ・ working 光電変換器の概要は以下のとおりです。

• Step1 −光電変換器は、光がその陰極に当たると電子を放出します。

• Step2 −光電変換器は、アノードに向かって電子が引き付けられるため、回路に電流Iを生成します。

私たちは見つけることができます sensitivity 次の式を使用して光電変換器の

$$ S = \ frac {I} {i} $$

どこ、

$ S $は光電変換器の感度です

$ I $は光電変換器の出力電流です

$ i $は、光電変換器の光入力の照明です。

熱電変換器

アクティブなトランスデューサーは thermo electric transducer、温度入力に相当する電気量を生成する場合。次の2つのトランスデューサーは、熱電トランスデューサーの例です。

• サーミスタトランスデューサ
• 熱電対トランスデューサ

それでは、これら2つのトランスデューサーについて1つずつ説明しましょう。

サーミスタトランスデューサ

温度に依存する抵抗器は熱抵抗器と呼ばれます。要するに、それは呼ばれますThermistor。サーミスタの温度係数は負です。つまり、温度が上昇すると、サーミスタの抵抗が減少します。

Mathematically、サーミスタの抵抗と温度の関係は次のように表すことができます。

$$ R_ {1} = R_ {2} e ^ \ left（\ beta \ left [\ frac {1} {T_ {1}}-\ frac {1} {T_ {2}} \ right] \ right） $$

Where、

$ R_ {1} $は、温度$ {T_ {1}} ^ {0} K $でのサーミスタの抵抗です。

$ R_ {2} $は、温度$ {T_ {2}} ^ {0} K $でのサーミスタの抵抗です。

$ \ beta $は温度定数です

ザ・ advantage サーミスタトランスデューサの特徴は、高速で安定した応答を生成することです。

熱電対トランスデューサ

熱電対トランスデューサは、入力の温度変化に対応する出力電圧を生成します。2つの接合部を作成するために、異なる金属の2つのワイヤが結合されている場合、その構成全体が呼び出されます。Thermocouple。基本的な熱電対の回路図を以下に示します-

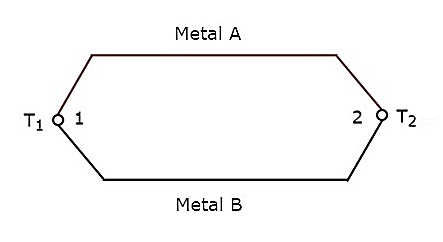
上記の熱電対には、AとBの2つの金属と、1と2の2つの接合部があります。接合部2で一定の基準温度$ T_ {2} $を考えます。接合部1の温度を$ T_ {1} $とします。熱電対はemf （起電力）、$ T_ {1} $と$ T_ {2} $の値が異なる場合。

つまり、熱電対は、2つの接合部1と2の間に温度差があり、それらの2つの接合部間の温度差に正比例する場合は常に起電力を生成します。 Mathematically、次のように表すことができます

$$ e \ alpha \ left（T_ {1} -T_ {2} \ right）$$

どこ、

$ e $は、熱電対によって生成される起電力です。

上記の熱電対回路は、実際のアプリケーションでは下の図に示すように表すことができます。

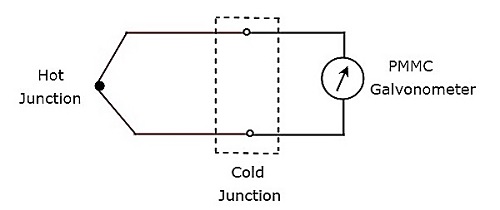
これらの2つの接合部を含むホット接合部とコールド接合部の間にある回路の部分は、基本的な熱電対の同等のモデルです。PMMC検流計は冷接点の両端に接続されており、冷接点の両端で生成された起電力に応じて偏向します。Thermocouple transducer 最も一般的に使用される熱電変換器です。

passive transducerは、受動素子の変動を生成するトランスデューサです。抵抗、インダクタ、コンデンサなどの受動素子について検討します。したがって、選択した受動素子に応じて、次の3つの受動トランスデューサが得られます。

• 抵抗膜トランスデューサ
• 誘導トランスデューサ
• 容量性トランスデューサー

それでは、これら3つのパッシブトランスデューサについて1つずつ説明しましょう。

抵抗膜トランスデューサ

パッシブトランスデューサは、 resistive transducer、抵抗値の変動（変化）が発生した場合。次の式resistance、金属導体のR。

$$ R = \ frac {\ rho \：l} {A} $$

どこ、

$ \ rho $は導体の抵抗率です

$ l $は導体の長さです

$ A $は導体の断面積です

抵抗値は、3つのパラメータ$ \ rho、l $、および$ A $に依存します。だから、私たちは作ることができますresistive transducers3つのパラメーター$ \ rho、l $、および$ A $のいずれかの変動に基づいています。これら3つのパラメータのいずれかが変化すると、抵抗値が変化します。

• 抵抗、Rはに正比例します resistivity指揮者の$ \ rho $。したがって、導体の抵抗率として、$ \ rho $は抵抗値を増加させ、Rも増加します。同様に、導体の抵抗率$ \ rho $が抵抗値を減少させると、Rも減少します。

• 抵抗、Rはに正比例します length指揮者の$ l $。したがって、導体の長さが$ l $になると抵抗の値が大きくなり、Rも大きくなります。同様に、導体の長さが$ l $になると抵抗の値が減少し、Rも減少します。

• 抵抗、Rはに反比例します cross sectional area指揮者の$ A $。したがって、導体の断面積として、$ A $は抵抗の値を増加させ、Rは減少させます。同様に、導体の断面積として、$ A $は抵抗の値を減少させ、Rは増加します。

誘導トランスデューサ

パッシブトランスデューサは、 inductive transducer、インダクタンス値の変動（変化）が発生した場合。次の式inductance、インダクタのL。

$ L = \ frac {N ^ {2}} {S} $式1

どこ、

$ N $はコイルの巻数です

$ S $はコイルの巻数です

次の式 reluctance、コイルのS。

$ S = \ frac {l} {\ mu A} $式2

どこ、

$ l $は磁気回路の長さです

$ \ mu $はコアの透磁率です

$ A $は、磁束が流れる磁気回路の面積です。

式1の式2を代入します。

$$ L = \ frac {N ^ {2}} {\ left（\ frac {l} {\ mu A} \ right）} $$

$ \ Rightarrow L = \ frac {N ^ {2} \ mu A} {l} $式3

式1と式3から、インダクタンス値は3つのパラメータ$ N、S $と$ \ mu $に依存すると結論付けることができます。だから、私たちは作ることができますinductive transducers3つのパラメータ$ N、S $および$ \ mu $のいずれかの変動に基づいています。なぜなら、これら3つのパラメータのいずれかが変化すると、インダクタンス値が変化するからです。

• インダクタンス、Lは2乗に正比例します number of turns of coil。したがって、コイルの巻き数に応じて、$ N $はインダクタンスの値を増加させ、$ L $も増加します。同様に、コイルの巻数が増えると、$ N $はインダクタンスの値を減らし、$ L $も減少します。

• インダクタンス、$ L $は反比例します reluctance of coil、$ S $。したがって、コイルの磁気抵抗として、$ S $はインダクタンスの値を増加させ、$ L $は減少させます。同様に、コイルの磁気抵抗として、$ S $はインダクタンスの値を減少させ、$ L $は増加します。

• インダクタンス、Lはに正比例します permeability of core、$ \ mu $。したがって、コアの透磁率、$ \ mu $がインダクタンスの値を増加させると、Lも増加します。同様に、コアの透磁率、$ \ mu $がインダクタンスの値を減少させると、Lも減少します。

容量性トランスデューサー

パッシブトランスデューサは、 capacitive transducer、静電容量値の変動（変化）が発生した場合。次の式capacitance、平行平板コンデンサのC。

$$ C = \ frac {\ varepsilon A} {d} $$

どこ、

$ \ varepsilon $は、誘電率または誘電率です。

$ A $は、2つのプレートの有効面積です。

$ d $は2つのプレートの有効面積です

静電容量の値は、3つのパラメーター$ \ varepsilon、A $、および$ d $に依存します。だから、私たちは作ることができますcapacitive transducers3つのパラメータ$ \ varepsilon、A $＆$ d $のいずれかの変動に基づいています。なぜなら、これら3つのパラメータのいずれかが変化すると、静電容量値が変化するからです。

• 静電容量、Cはに正比例します permittivity、$ \ varepsilon $。したがって、誘電率として、$ \ varepsilon $は静電容量の値を増加させ、Cも増加します。同様に、誘電率として、$ \ varepsilon $は静電容量の値を減少させ、Cも減少します。

• 静電容量、Cはに正比例します effective area of two plates、$ A $。したがって、2つのプレートの有効面積として、$ A $は静電容量の値を増加させ、Cも増加します。同様に、2つのプレートの有効面積として、$ A $は静電容量の値を減少させ、Cも減少します。

• 静電容量、Cはに反比例します distance between two plates、$ d $。したがって、2つのプレート間の距離が増加すると、$ d $は静電容量の値を増加させ、Cは減少します。同様に、2つのプレート間の距離として、$ d $は静電容量の値を減少させ、Cは増加します。

この章では、3つのパッシブトランスデューサについて説明しました。次の章では、各パッシブトランスデューサの例について説明します。

ザ・ physical quantities変位、速度、力、温度などはすべて非電気的な量です。アクティブトランスデューサは、物理量を電気信号に変換します。一方、パッシブトランスデューサは物理量をパッシブエレメントの変動に変換します。

したがって、要件に基づいて、アクティブトランスデューサまたはパッシブトランスデューサのいずれかを選択できます。この章では、パッシブトランスデューサを使用して変位を測定する方法について説明します。ある点から別の点に直線で移動する物体の場合、それらの2点間の長さはdisplacement。

以下があります three passive transducers

• 抵抗膜トランスデューサ
• 誘導トランスデューサ
• 容量性トランスデューサー

ここで、これら3つのパッシブトランスデューサを使用した変位の測定について1つずつ説明します。

抵抗変換器を使用した変位の測定

ザ・ circuit diagram 変位の測定に使用される抵抗変換器の概要を下図に示します。

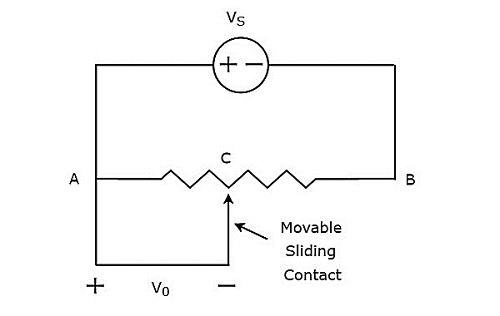
上記の回路は、ポテンショメータと電圧源$ V_ {S} $で構成されています。これら2つはA点とB点に関して並列に接続されていると言えます。ポテンショメータにはスライド接点があり、これは変更可能です。したがって、点Cは可変点です。上記の回路では、output voltage、$ V_ {0} $は、ポイントAとCで測定されます。

Mathematically、電圧と距離の関係は次のように表すことができます。

$$ \ frac {V_ {0}} {V_ {S}} = \ frac {AC} {AB} $$

したがって、変位を測定する本体をすべり接触に接続する必要があります。したがって、体が直線的に動くときはいつでも、点Cも変化します。これにより、出力電圧$ V_ {0} $もそれに応じて変化します。

この場合、出力電圧$ V_ {0} $を測定することで変位を見つけることができます。

誘導トランスデューサを使用した変位の測定

ザ・ circuit diagram 変位の測定に使用される誘導トランスデューサの概要を下図に示します。

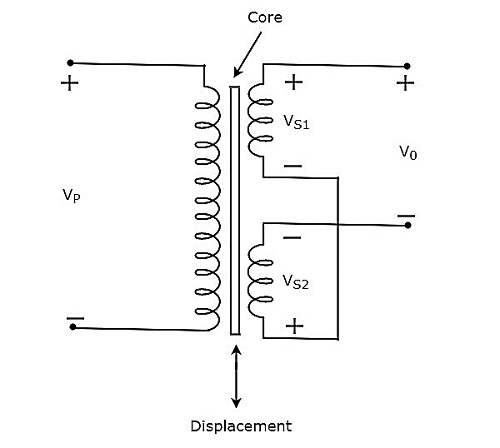
上記の回路にあるトランスには、1次巻線と2つの2次巻線があります。ここでは、2つの2次巻線の終点が結合されています。したがって、これらの2つの2次巻線はで接続されていると言えます。series opposition。

電圧$ V_ {P} $は、トランスの一次巻線に印加されます。各二次巻線に発生する電圧をð?? '‰ð??'†1およびð?? '‰ð??'†2とします。出力電圧$ V_ {0} $は、2つの2次巻線の開始点で取得されます。

Mathematically、出力電圧、ð?? '‰0は次のように書くことができます

$$ V_ {0} = V_ {S1} -V_ {S2} $$

上記の回路にあるトランスは differential transformer、$ V_ {S1} $と$ V_ {S2} $の差である出力電圧を生成するためです。

• コアが中央位置にある場合、出力電圧$ V_ {0} $はゼロに等しくなります。なぜなら、$ V_ {S1} $と$ V_ {S2} $のそれぞれの大きさと位相は同じだからです。

• コアが中央位置にない場合、出力電圧$ V_ {0} $はある程度の大きさと位相を持ちます。なぜなら、$ V_ {S1} $と$ V_ {S2} $のそれぞれの大きさと位相は等しくないからです。

したがって、変位を測定する物体を中心コアに接続する必要があります。そのため、体が直線的に動くと、コアの中心位置が変化します。これにより、出力電圧$ V_ {0} $もそれに応じて変化します。

この場合、私たちは見つけることができます displacement出力電圧$ V_ {0} $を測定します。出力電圧の大きさと位相$ V_ {0} $は、それぞれ物体の変位とその方向を表します。

容量性トランスデューサを使用した変位の測定

ザ・ circuit diagram 変位を測定するために使用される容量性トランスデューサの例を下の図に示します。

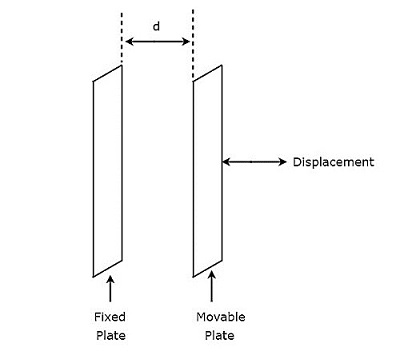
ザ・ capacitor上記の回路に存在する、は2つの平行なプレートを持っています。その中で、一方のプレートは固定されており、もう一方のプレートは可動プレートです。このため、これら2つのプレート間の間隔も異なります。静電容量の値は、コンデンサの2つのプレート間の間隔が変化するにつれて変化します。

したがって、私たちはその体を接続する必要があります displacementコンデンサの可動プレートに対して測定されます。したがって、本体が直線的に移動するたびに、コンデンサの2つのプレート間の間隔が変化します。これにより、静電容量値が変化します。

データ収集に使用されるシステムは、 data acquisition systems。これらのデータ収集システムは、データの変換、データの保存、データの送信、データの処理などのタスクを実行します。

データ収集システムは次のことを考慮します analog signals。

• DCおよびAC電圧、DCおよびAC電流、抵抗などの電気量を直接測定して得られるアナログ信号。

• LVDT、熱電対などのトランスデューサから得られるアナログ信号。

データ収集システムの種類

データ収集システムは、次のように分類できます。 two types。

• アナログデータ収集システム
• デジタルデータ収集システム

ここで、これら2種類のデータ収集システムについて1つずつ説明します。

アナログデータ収集システム

アナログ信号で操作できるデータ収集システムは、 analog data acquisition systems。以下は、アナログデータ収集システムのブロックです。

• Transducer −物理量を電気信号に変換します。

• Signal conditioner −信号の目的の部分の増幅や選択などの機能を実行します。

• Display device −監視目的で入力信号を表示します。

• Graphic recording instruments −これらは、入力データの記録を永続的に作成するために使用できます。

• Magnetic tape instrumentation −入力データの取得、保存、再生に使用します。

デジタルデータ収集システム

デジタル信号で操作できるデータ収集システムは、 digital data acquisition systems。そのため、情報を保存または表示するためにデジタルコンポーネントを使用しています。

主に、以下 operations デジタルデータ収集で行われます。

• アナログ信号の取得
• アナログ信号のデジタル信号またはデジタルデータへの変換
• デジタル信号またはデジタルデータの処理

以下はのブロックです Digital data acquisition systems。

• Transducer −物理量を電気信号に変換します。

• Signal conditioner −信号の目的の部分の増幅や選択などの機能を実行します。

• Multiplexer−複数の入力の1つを出力に接続します。したがって、シリアルコンバータに並列として機能します。

• Analog to Digital Converter −アナログ入力を同等のデジタル出力に変換します。

• Display device −データをデジタル形式で表示します。

• Digital Recorder −データをデジタル形式で記録するために使用されます。

データ収集システムは、生物医学や航空宇宙などのさまざまなアプリケーションで使用されています。したがって、要件に基づいて、アナログデータ収集システムまたはデジタルデータ収集システムのいずれかを選択できます。