MATLAB-微分

MATLABは diffシンボリック導関数を計算するためのコマンド。最も単純な形式では、区別したい関数を引数としてdiffコマンドに渡します。

たとえば、関数f（t）= 3t 2 + 2t - 2の導関数を計算してみましょう。

例

スクリプトファイルを作成し、次のコードを入力します-

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

上記のコードをコンパイルして実行すると、次の結果が得られます。

ans =
6*t - 4/t^3

以下は、上記の計算に相当するオクターブです-

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octaveはコードを実行し、次の結果を返します-

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

微分の基本規則の検証

関数を微分するためのさまざまな方程式や規則を簡単に述べ、これらの規則を検証しましょう。この目的のために、1次導関数の場合はf '（x）、2次導関数の場合はf "（x）と記述します。

差別化のルールは次のとおりです-

ルール1

任意の関数fとg、および任意の実数aとbは、関数−の導関数です。

h(x) = af(x) + bg(x) xに関しては−で与えられます

h'(x) = af'(x) + bg'(x)

ルール2

ザ・ sum そして subtraction ルールは、fとgが2つの関数である場合、f 'とg'はそれぞれそれらの導関数であると述べています。

（（f + g)' = f' + g'

(f - g)' = f' - g'

ルール3

ザ・ product ルールは、fとgが2つの関数である場合、f 'とg'はそれぞれそれらの導関数であると述べています。

(f.g)' = f'.g + g'.f

ルール4

ザ・ quotient ルールは、fとgが2つの関数である場合、f 'とg'はそれぞれそれらの導関数であると述べています。

(f/g)' = (f'.g - g'.f)/g2

ルール5

ザ・ polynomial または基本的なべき乗則は、 y = f(x) = xn、その後 f' = n. x(n-1)

このルールの直接の結果は、定数の導関数がゼロになることです。 y = k、任意の定数、その後

f' = 0

ルール6

ザ・ chain ルールは、関数の関数の導関数は、 h(x) = f(g(x)) xに関しては、

h'(x)= f'(g(x)).g'(x)

例

スクリプトファイルを作成し、次のコードを入力します-

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

ファイルを実行すると、MATLABは次の結果を表示します-

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

以下は、上記の計算に相当するオクターブです-

pkg load symbolic
symbols

x = sym("x");
t = sym("t");

f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 

f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 

f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 

f = (x^2 + 1)^17 
der5 = differentiate(f,x) 

f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octaveはコードを実行し、次の結果を返します-

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

指数関数、対数関数、三角関数の導関数

次の表は、一般的に使用される指数関数、対数関数、三角関数の導関数を示しています。

関数 デリバティブ
ca.x c a.x .ln ca（lnは自然対数）
ex e x
ln x 1 / x
lncx 1 / x.ln c
xx x x。（1 + ln x）
sin(x) cos（x）
cos(x) -sin（x）
tan(x) 秒2（x）、または1 / cos 2（x）、または1 + tan 2（x）
cot(x) -csc 2（x）、または-1 / sin 2（x）、または-（1 + cot 2（x））
sec(x) sec（x）.tan（x）
csc(x) -csc（x）.cot（x）

例

スクリプトファイルを作成し、次のコードを入力します-

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

ファイルを実行すると、MATLABは次の結果を表示します-

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

以下は、上記の計算に相当するオクターブです-

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octaveはコードを実行し、次の結果を返します-

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

高階導関数の計算

関数fの高階導関数を計算するには、構文を使用します。 diff(f,n)。

関数y = f（x）= x .e -3xの2階微分を計算してみましょう。

f = x*exp(-3*x);
diff(f, 2)

MATLABはコードを実行し、次の結果を返します-

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

以下は、上記の計算に相当するオクターブです-

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octaveはコードを実行し、次の結果を返します-

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

例

この例では、問題を解決しましょう。その関数を考えるとy = f(x) = 3 sin(x) + 7 cos(5x)。方程式かどうかを調べる必要がありますf" + f = -5cos(2x) 当てはまります。

スクリプトファイルを作成し、次のコードを入力します-

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

ファイルを実行すると、次の結果が表示されます-

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

以下は、上記の計算に相当するオクターブです-

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octaveはコードを実行し、次の結果を返します-

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

曲線の最大値と最小値を見つける

グラフの極大値と極小値を検索する場合、基本的に、特定の場所での関数のグラフ上の最高点または最低点、またはシンボリック変数の特定の範囲の値を検索します。

関数y = f（x）の場合、グラフの傾きがゼロであるグラフ上の点は次のように呼ばれます。 stationary points。言い換えれば、停留点はf '（x）= 0の場所です。

微分する関数の停留点を見つけるには、導関数をゼロに設定し、方程式を解く必要があります。

例

関数f（x）= 2x 3 + 3x 2 − 12x +17の停留点を見つけましょう

次の手順を実行します-

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLABはコードを実行し、次のプロットを返します-

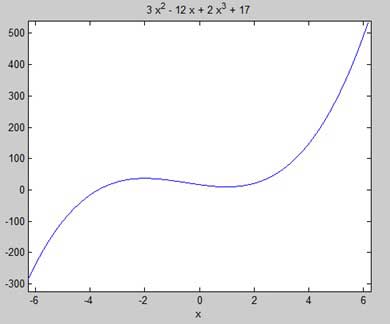
上記の例のオクターブに相当するコードは次のとおりです-

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLABはコードを実行し、次のプロットを返します-

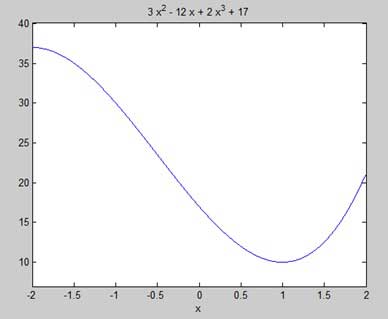
上記の例のオクターブに相当するコードは次のとおりです-

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

MATLABはコードを実行し、次の結果を返します-

g =
   6*x^2 + 6*x - 12

上記の計算に相当するオクターブは次のとおりです-

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octaveはコードを実行し、次の結果を返します-

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

MATLABはコードを実行し、次の結果を返します-

s =
   1
   -2

以下は、上記の計算に相当するオクターブです-

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octaveはコードを実行し、次の結果を返します-

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. シンボリック関数の値は、 subs コマンド。

subs(y, 1), subs(y, -2)

MATLABはコードを実行し、次の結果を返します-

ans =
   10
ans =
   37

以下は、上記の計算に相当するオクターブです-

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

したがって、関数f（x）= 2x 3 + 3x 2 − 12x + 17の区間[-2,2]の最小値と最大値は、10と37です。

微分方程式を解く

MATLABは dsolve 微分方程式を象徴的に解くためのコマンド。

の最も基本的な形式 dsolve 単一の方程式の解を見つけるためのコマンドは

dsolve('eqn')

ここで、eqnは、方程式を入力するために使用されるテキスト文字列です。

これは、MATLABがC1、C2などにラベル付けする任意の定数のセットを持つシンボリックソリューションを返します。

問題の初期条件と境界条件を、次の方程式に続くコンマ区切りのリストとして指定することもできます。

dsolve('eqn','cond1', 'cond2',…)

dsolveコマンドを使用するために、 derivatives are indicated with a D。たとえば、f '（t）= -2 * f + cost（t）のような方程式は-として入力されます

'Df = -2*f + cos(t)'

高階導関数は、導関数の順序でDをたどることによって示されます。

たとえば、方程式f "（x）+ 2f '（x）= 5sin3xは、次のように入力する必要があります。

'D2y + 2Dy = 5*sin(3*x)'

一階微分方程式の簡単な例を取り上げましょう：y '= 5y。

s = dsolve('Dy = 5*y')

MATLABはコードを実行し、次の結果を返します-

s =
   C2*exp(5*t)

2階微分方程式の別の例を次のように取り上げます。y "-y = 0、y（0）= -1、y '（0）= 2。

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLABはコードを実行し、次の結果を返します-

ans =
   exp(t)/2 - (3*exp(-t))/2
ja/tutorial
es/tutorial
de/tutorial
fr/tutorial
th/tutorial
pt/tutorial
ru/tutorial
vi/tutorial
it/tutorial
ko/tutorial
tr/tutorial
id/tutorial
pl/tutorial
hi/tutorial
japost
espost
depost
frpost
thpost
ptpost
rupost
vipost
itpost
kopost
trpost
idpost
plpost
hipost

© Copyright 2021 - 2024 | All Rights Reserved