단위 분수 모서리 길이를 가진 입방체로 만든 솔리드의 볼륨
여기서 우리는 단위 분율 가장자리 길이를 가진 입방체로 만들어진 고체의 부피를 찾습니다. 예를 들어 가장자리 길이 가 $ \ frac {1} {2} $ 인치 인 작은 입방체로 만들어진 3 인치 × 3 인치 × 3 치수의 솔리드를 생각해보십시오 .
이 경우 솔리드는 $ \ frac {1} {2} $ 인치 가장자리 길이 의 6 × 6 × 6 작은 입방체로 구성 됩니다. 따라서이 경우 고체의 부피는
볼륨 = lwh = $ 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} $
= 3 × 3 × 3 = 27 입방 인치
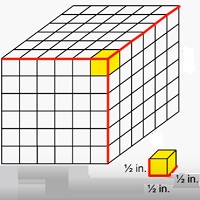
단위 부분 가장자리 길이를 가진 입방체로 만들어진 고체 부피 공식
솔리드가 모서리 큐브라고 가정합니다.
b = 각 모서리를 따라 단위 분수 모서리 길이가있는 큐브 수
k = 단위 부분 가장자리 길이
Volume of solid = b × k × b × k × b × k cubic units
단위 분율 가장자리 길이를 가진 다음 입방체의 고체 부피를 찾으십시오. 각 프리즘 단위는 cm 단위로 측정됩니다 (축척이 아님).
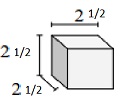
해결책
Step 1:
단위 분율 가장자리 길이가 $ \ frac {1} {2} $ cm 인 입방체의 솔리드
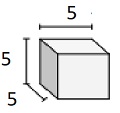
Step 2:
볼륨 V = lwh = $ 2 \ frac {1} {2} \ times 2 \ frac {1} {2} \ times 2 \ frac {1} {2} $
= $ 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} $
= $ 15 \ frac {5} {8} $ cu cm
단위 분율 가장자리 길이를 가진 다음 입방체의 고체 부피를 찾으십시오. 각 프리즘 단위는 cm 단위로 측정됩니다 (축척이 아님).
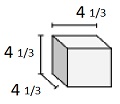
해결책
Step 1:
단위 분율 가장자리 길이가 $ \ frac {1} {3} $ cm 인 정육면체
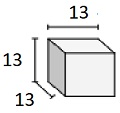
Step 2:
볼륨 V = lwh = $ 4 \ frac {1} {3} \ times 4 \ frac {1} {3} \ times 4 \ frac {1} {3} $
= $ 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} $
= $ 81 \ frac {10} {27} $ cu cm