Python을 사용한 AI – 시계열 데이터 분석

주어진 입력 시퀀스에서 다음을 예측하는 것은 기계 학습에서 또 다른 중요한 개념입니다. 이 장에서는 시계열 데이터 분석에 대한 자세한 설명을 제공합니다.

소개

시계열 데이터는 일련의 특정 시간 간격에있는 데이터를 의미합니다. 기계 학습에서 시퀀스 예측을 구축하려면 순차적 인 데이터와 시간을 처리해야합니다. 시리즈 데이터는 순차적 데이터의 추상입니다. 데이터 순서는 순차 데이터의 중요한 기능입니다.

시퀀스 분석 또는 시계열 분석의 기본 개념

시퀀스 분석 또는 시계열 분석은 이전에 관찰 된 것을 기반으로 주어진 입력 시퀀스에서 다음을 예측하는 것입니다. 예측은 다음에 올 수있는 모든 것이 될 수 있습니다 : 기호, 숫자, 다음 날 날씨, 다음 연설 용어 등. 시퀀스 분석은 주식 시장 분석, 일기 예보 및 제품 추천과 같은 애플리케이션에서 매우 편리 할 수 ​​있습니다.

Example

시퀀스 예측을 이해하려면 다음 예제를 고려하십시오. 여기A,B,C,D 주어진 값이고 당신은 그 값을 예측해야합니다 E 시퀀스 예측 모델을 사용합니다.

유용한 패키지 설치

Python을 사용한 시계열 데이터 분석을 위해 다음 패키지를 설치해야합니다.

판다

Pandas는 Python을위한 고성능의 데이터 구조 사용 및 데이터 분석 도구를 제공하는 오픈 소스 BSD 라이선스 라이브러리입니다. 다음 명령을 사용하여 Pandas를 설치할 수 있습니다.

pip install pandas

Anaconda를 사용 중이고 다음을 사용하여 설치하려는 경우 conda 패키지 관리자, 다음 명령을 사용할 수 있습니다-

conda install -c anaconda pandas

hmmlearn

Python으로 HMM (Hidden Markov Models)을 학습하기위한 간단한 알고리즘과 모델로 구성된 오픈 소스 BSD 라이선스 라이브러리입니다. 다음 명령을 사용하여 설치할 수 있습니다.

pip install hmmlearn

Anaconda를 사용 중이고 다음을 사용하여 설치하려는 경우 conda 패키지 관리자, 다음 명령을 사용할 수 있습니다-

conda install -c omnia hmmlearn

PyStruct

구조화 된 학습 및 예측 라이브러리입니다. PyStruct에서 구현 된 학습 알고리즘에는 조건부 랜덤 필드 (CRF), 최대 마진 마코프 랜덤 네트워크 (M3N) 또는 구조 지원 벡터 머신과 같은 이름이 있습니다. 다음 명령을 사용하여 설치할 수 있습니다.

pip install pystruct

CVXOPT

파이썬 프로그래밍 언어를 기반으로 볼록 최적화에 사용됩니다. 또한 무료 소프트웨어 패키지입니다. 다음 명령을 사용하여 설치할 수 있습니다.

pip install cvxopt

Anaconda를 사용 중이고 다음을 사용하여 설치하려는 경우 conda 패키지 관리자, 다음 명령을 사용할 수 있습니다-

conda install -c anaconda cvdoxt

Pandas : 시계열 데이터에서 통계 처리, 분할 및 추출

Pandas는 시계열 데이터로 작업해야하는 경우 매우 유용한 도구입니다. Pandas의 도움으로 다음을 수행 할 수 있습니다.

• 다음을 사용하여 날짜 범위를 만듭니다. pd.date_range 꾸러미

• 다음을 사용하여 날짜가있는 판다 색인 pd.Series 꾸러미

• 다음을 사용하여 재 샘플링을 수행합니다. ts.resample 꾸러미

• 주파수 변경

예

다음 예제는 Pandas를 사용하여 시계열 데이터를 처리하고 분할하는 방법을 보여줍니다. 여기서는 Monthly Arctic Oscillation 데이터를 사용하고 있습니다.이 데이터는 월간 .ao.index.b50.current.ascii 에서 다운로드 할 수 있으며 텍스트 형식으로 변환하여 사용할 수 있습니다.

시계열 데이터 처리

시계열 데이터를 처리하려면 다음 단계를 수행해야합니다.

첫 번째 단계는 다음 패키지를 가져 오는 것입니다.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

다음으로, 아래 주어진 코드와 같이 입력 파일에서 데이터를 읽는 함수를 정의하십시오.

def read_data(input_file):
   input_data = np.loadtxt(input_file, delimiter = None)

이제이 데이터를 시계열로 변환합니다. 이를 위해 시계열의 날짜 범위를 만듭니다. 이 예에서는 데이터 빈도로 한 달을 유지합니다. 파일에는 1950 년 1 월부터 시작되는 데이터가 있습니다.

dates = pd.date_range('1950-01', periods = input_data.shape[0], freq = 'M')

이 단계에서는 아래와 같이 Pandas Series의 도움으로 시계열 데이터를 생성합니다.

output = pd.Series(input_data[:, index], index = dates)	
return output
	
if __name__=='__main__':

여기에 표시된대로 입력 파일의 경로를 입력하십시오-

input_file = "/Users/admin/AO.txt"

이제 여기에 표시된대로 열을 timeseries 형식으로 변환하십시오.

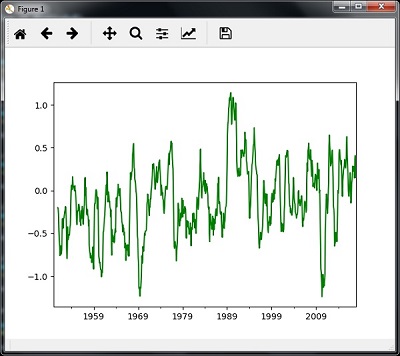
timeseries = read_data(input_file)

마지막으로 표시된 명령을 사용하여 데이터를 플로팅하고 시각화합니다.

plt.figure()
timeseries.plot()
plt.show()

다음 이미지와 같이 플롯을 관찰합니다.

시계열 데이터 슬라이스

슬라이싱에는 시계열 데이터의 일부만 검색하는 작업이 포함됩니다. 예제의 일부로 1980 년부터 1990 년까지만 데이터를 분할합니다.이 작업을 수행하는 다음 코드를 살펴보십시오.

timeseries['1980':'1990'].plot()
   <matplotlib.axes._subplots.AxesSubplot at 0xa0e4b00>

plt.show()

시계열 데이터를 분할하는 코드를 실행하면 여기 이미지와 같이 다음 그래프를 볼 수 있습니다.

시계열 데이터에서 통계 추출

중요한 결론을 내려야하는 경우 주어진 데이터에서 일부 통계를 추출해야합니다. 평균, 분산, 상관, 최대 값 및 최소값이 이러한 통계의 일부입니다. 주어진 시계열 데이터에서 이러한 통계를 추출하려면 다음 코드를 사용할 수 있습니다.

평균

당신은 사용할 수 있습니다 mean() 평균을 구하기위한 함수

timeseries.mean()

그런 다음 논의 된 예에서 관찰 할 출력은 다음과 같습니다.

-0.11143128165238671

최고

당신은 사용할 수 있습니다 max() 최대 값을 찾기위한 함수

timeseries.max()

그런 다음 논의 된 예에서 관찰 할 출력은 다음과 같습니다.

3.4952999999999999

최저한의

min () 함수를 사용하여 최소값을 찾을 수 있습니다.

timeseries.min()

그런 다음 논의 된 예에서 관찰 할 출력은 다음과 같습니다.

-4.2656999999999998

한 번에 모든 것을 얻기

한 번에 모든 통계를 계산하려면 다음을 사용할 수 있습니다. describe() 여기에 표시된 기능-

timeseries.describe()

그런 다음 논의 된 예에서 관찰 할 출력은 다음과 같습니다.

count   817.000000
mean     -0.111431
std       1.003151
min      -4.265700
25%      -0.649430
50%      -0.042744
75%       0.475720
max       3.495300
dtype: float64

재 샘플링

데이터를 다른 시간 빈도로 리샘플링 할 수 있습니다. 리샘플링을 수행하는 두 가지 매개 변수는 다음과 같습니다.

• 기간
• Method

mean ()을 사용한 재 샘플링

다음 코드를 사용하여 기본 방법 인 mean () 방법으로 데이터를 다시 샘플링 할 수 있습니다.

timeseries_mm = timeseries.resample("A").mean()
timeseries_mm.plot(style = 'g--')
plt.show()

그런 다음 mean ()을 사용한 리샘플링의 출력으로 다음 그래프를 볼 수 있습니다.

median ()을 사용한 재 샘플링

다음 코드를 사용하여 데이터를 다시 샘플링 할 수 있습니다. median()방법-

timeseries_mm = timeseries.resample("A").median()
timeseries_mm.plot()
plt.show()

그런 다음 median ()을 사용한 리샘플링의 출력으로 다음 그래프를 볼 수 있습니다.

롤링 평균

다음 코드를 사용하여 롤링 (이동) 평균을 계산할 수 있습니다.

timeseries.rolling(window = 12, center = False).mean().plot(style = '-g')
plt.show()

그런 다음 롤링 (이동) 평균의 출력으로 다음 그래프를 볼 수 있습니다.

은닉 마르코프 모델 (HMM)에 의한 순차 데이터 분석

HMM은 시계열 주식 시장 분석, 건강 검진, 음성 인식 등 연속성과 확장 성이있는 데이터에 널리 사용되는 통계 모델입니다. 이 섹션에서는 HMM (Hidden Markov Model)을 사용한 순차 데이터 분석에 대해 자세히 다룹니다.

은닉 마르코프 모델 (HMM)

HMM은 미래 통계의 확률이 이전 상태가 아닌 현재 프로세스 상태에만 의존한다는 가정을 바탕으로 Markov 체인의 개념을 기반으로 구축 된 확률 모델입니다. 예를 들어 동전을 던질 때 다섯 번째 던지기의 결과가 앞면이라고 말할 수 없습니다. 코인에는 메모리가없고 다음 결과는 이전 결과에 의존하지 않기 때문입니다.

수학적으로 HMM은 다음 변수로 구성됩니다.

주 (S)

HMM에 존재하는 숨겨진 상태 또는 잠재 상태의 집합입니다. S로 표시됩니다.

출력 기호 (O)

HMM에있는 가능한 출력 기호 세트입니다. O로 표시됩니다.

상태 전이 확률 매트릭스 (A)

한 상태에서 다른 상태로 전환 할 확률입니다. A로 표시됩니다.

관측 방출 확률 매트릭스 (B)

특정 상태에서 심볼을 방출 / 관찰 할 확률입니다. B로 표시됩니다.

사전 확률 행렬 (Π)

시스템의 다양한 상태에서 특정 상태에서 시작할 확률입니다. Π로 표시됩니다.

따라서 HMM은 다음과 같이 정의 할 수 있습니다. = (S,O,A,B,),

어디,

• S = {s₁,s₂,…,s_N} N 개의 가능한 상태의 집합입니다.
• O = {o₁,o₂,…,o_M} M 개의 가능한 관측 기호 세트입니다.
• A는 NN 상태 전이 확률 매트릭스 (TPM),
• B는 NM 관찰 또는 EPM (Emission Probability Matrix),
• π는 N 차원 초기 상태 확률 분포 벡터입니다.

예 : 주식 시장 데이터 분석

이 예에서는 주식 시장의 데이터를 단계별로 분석하여 HMM이 순차 또는 시계열 데이터로 작동하는 방식에 대한 아이디어를 얻을 것입니다. 이 예제는 Python으로 구현하고 있습니다.

아래와 같이 필요한 패키지를 가져옵니다.

import datetime
import warnings

이제 주식 시장 데이터를 사용하십시오. matpotlib.finance 여기에 표시된대로 패키지-

import numpy as np
from matplotlib import cm, pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator
try:
   from matplotlib.finance import quotes_historical_yahoo_och1
except ImportError:
   from matplotlib.finance import (
      quotes_historical_yahoo as quotes_historical_yahoo_och1)

from hmmlearn.hmm import GaussianHMM

시작 날짜와 종료 날짜, 즉 여기에 표시된 두 특정 날짜 사이의 데이터를로드합니다.

start_date = datetime.date(1995, 10, 10)
end_date = datetime.date(2015, 4, 25)
quotes = quotes_historical_yahoo_och1('INTC', start_date, end_date)

이 단계에서는 매일 닫는 따옴표를 추출합니다. 이를 위해 다음 명령을 사용하십시오-

closing_quotes = np.array([quote[2] for quote in quotes])

이제 우리는 매일 거래되는 주식의 양을 추출 할 것입니다. 이를 위해 다음 명령을 사용하십시오-

volumes = np.array([quote[5] for quote in quotes])[1:]

여기에서 아래 표시된 코드를 사용하여 종가의 백분율 차이를 가져옵니다.

diff_percentages = 100.0 * np.diff(closing_quotes) / closing_quotes[:-]
dates = np.array([quote[0] for quote in quotes], dtype = np.int)[1:]
training_data = np.column_stack([diff_percentages, volumes])

이 단계에서는 Gaussian HMM을 만들고 훈련시킵니다. 이를 위해 다음 코드를 사용하십시오-

hmm = GaussianHMM(n_components = 7, covariance_type = 'diag', n_iter = 1000)
with warnings.catch_warnings():
   warnings.simplefilter('ignore')
   hmm.fit(training_data)

이제 표시된 명령을 사용하여 HMM 모델을 사용하여 데이터를 생성합니다.

num_samples = 300
samples, _ = hmm.sample(num_samples)

마지막으로,이 단계에서 우리는 그래프 형태로 출력으로 거래되는 주식의 차이 비율과 볼륨을 플로팅하고 시각화합니다.

다음 코드를 사용하여 차이 백분율을 플로팅하고 시각화하십시오.

plt.figure()
plt.title('Difference percentages')
plt.plot(np.arange(num_samples), samples[:, 0], c = 'black')

다음 코드를 사용하여 거래 된 주식의 양을 플롯하고 시각화하십시오.

plt.figure()
plt.title('Volume of shares')
plt.plot(np.arange(num_samples), samples[:, 1], c = 'black')
plt.ylim(ymin = 0)
plt.show()